算法题总结(十)——二叉树上
#二叉树的递归遍历
// 前序遍历·递归·LC144_二叉树的前序遍历
class Solution {public List<Integer> preorderTraversal(TreeNode root) {List<Integer> result = new ArrayList<Integer>(); //也可以把result 作为全局变量,只需要一个函数即可。preorder(root, result);return result;}public void preorder(TreeNode root, List<Integer> result) {if (root == null) {return;}result.add(root.val);preorder(root.left, result);preorder(root.right, result);}
}
// 中序遍历·递归·LC94_二叉树的中序遍历
class Solution {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> res = new ArrayList<>();inorder(root, res);return res;}void inorder(TreeNode root, List<Integer> list) {if (root == null) {return;}inorder(root.left, list);list.add(root.val); // 注意这一句inorder(root.right, list);}
}
// 后序遍历·递归·LC145_二叉树的后序遍历
class Solution {public List<Integer> postorderTraversal(TreeNode root) {List<Integer> res = new ArrayList<>();postorder(root, res);return res;}void postorder(TreeNode root, List<Integer> list) {if (root == null) {return;}postorder(root.left, list);postorder(root.right, list);list.add(root.val); // 注意这一句}
}
后面写二叉树的递归算法,****就是要注意1、采用什么递归遍历 2、对结点的处理逻辑
一般是中左右,对中结点进行处理。
如果需要用到左右结点的返回值的,使用后续遍历,左右中。
#二叉树的迭代遍历
前序和中序是完全两种代码风格,这是因为前序遍历中访问节点(遍历节点)和处理节点(将元素放进result数组中)可以同步处理****,但是中序就无法做到同步!
对于中序遍历可以用一个指针来访问节点,访问到最底层,每次将访问的节点放进栈,如果访问到了最底层,将访问的节点放进栈。
再来看后序遍历,先序遍历是中左右,后续遍历是左右中,那么我们只需要调整一下先序遍历的代码顺序,就变成中右左的遍历顺序,然后在反转result数组,输出的结果顺序就是左右中了。
二叉树的非递归遍历要使用栈。
// 前序遍历顺序:中-左-右,入栈顺序:中-右-左
class Solution {public List<Integer> preorderTraversal(TreeNode root) {List<Integer> result = new ArrayList<>();if (root == null){return result; //返回空链表}Stack<TreeNode> stack = new Stack<>();stack.push(root);while (!stack.isEmpty()){TreeNode node = stack.pop();result.add(node.val);if (node.right != null){stack.push(node.right);}if (node.left != null){stack.push(node.left);}}return result;}
}// 中序遍历顺序: 左-中-右 入栈顺序: 左-右
class Solution {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> result = new ArrayList<>();if (root == null){return result;}Stack<TreeNode> stack = new Stack<>();TreeNode cur = root;while (cur != null || !stack.isEmpty()){if (cur != null){ // 指针来访问节点,访问到最底层stack.push(cur); // 指针来访问节点,访问到最底层 不等于空,入栈并指向左孩子cur = cur.left;}else{ //从栈里弹出的数据,就是要处理的数据(放进result数组里的数据)cur = stack.pop();result.add(cur.val); //中cur = cur.right; //右}}return result;}
}// 后序遍历顺序 左-右-中 入栈顺序:中-左-右 出栈顺序:中-右-左, 最后翻转结果
class Solution {public List<Integer> postorderTraversal(TreeNode root) {List<Integer> result = new ArrayList<>();if (root == null){return result;}Stack<TreeNode> stack = new Stack<>();stack.push(root);while (!stack.isEmpty()){TreeNode node = stack.pop();result.add(node.val);if (node.left != null){ //先放左子树,再放右子树stack.push(node.left);}if (node.right != null){stack.push(node.right);}}Collections.reverse(result); return result;}
}
二叉树的层序遍历
102、二叉树的层序遍历
一层一层的处理
class Solution {public List<List<Integer>> levelOrder(TreeNode root) {List<List<Integer>> result= new ArrayList<>();if(root==null) return result;Queue<TreeNode> queue =new LinkedList<>();queue.add(root);while(!queue.isEmpty()) //控制层数{List<Integer> tmp=new ArrayList<>(); //每次都新建一个ArrayList 防止被修改int len=queue.size(); //每层的个数while(len>0) //遍历每层的结点,也可以使用for循环{TreeNode node =queue.poll();tmp.add(node.val);if(node.left!=null)queue.add(node.left);if(node.right!=null)queue.add(node.right);len--;}result.add(tmp);}return result;}
}
#107、二叉树的层序遍历二
给你二叉树的根节点 root ,返回其节点值 自底向上的层序遍历 。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
示例 1:
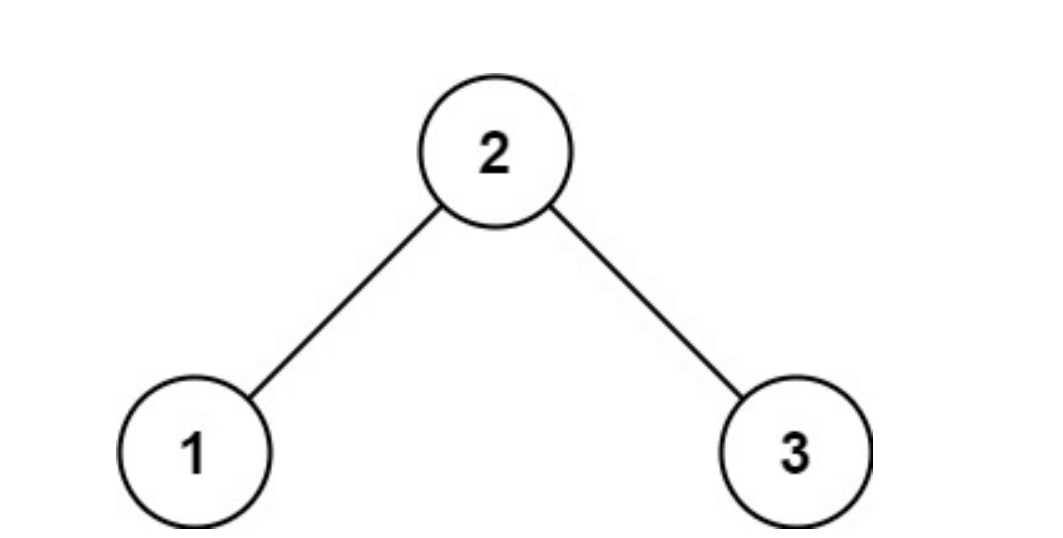
输入:root = [3,9,20,null,null,15,7]
输出:[[15,7],[9,20],[3]]
示例 2:
输入:root = [1]
输出:[[1]]
示例 3:
输入:root = []
输出:[]
把每层的列表从头插入结果中就可以
class Solution {public List<List<Integer>> levelOrderBottom(TreeNode root) {List<List<Integer>> ans= new ArrayList<List<Integer>>();if(root==null) return ans;Queue<TreeNode> queue =new LinkedList<>();queue.add(root);while(!queue.isEmpty()){List<Integer> tmp= new ArrayList<>();int len=queue.size();while(len>0){TreeNode node =queue.poll();tmp.add(node.val);if(node.left!=null) queue.add(node.left);if(node.right!=null)queue.add(node.right);len--;}ans.add(0,tmp); //每次都从头开始插入}return ans;}
}
#199、二叉树的右视图
给定一个二叉树的 根节点root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
示例 1:
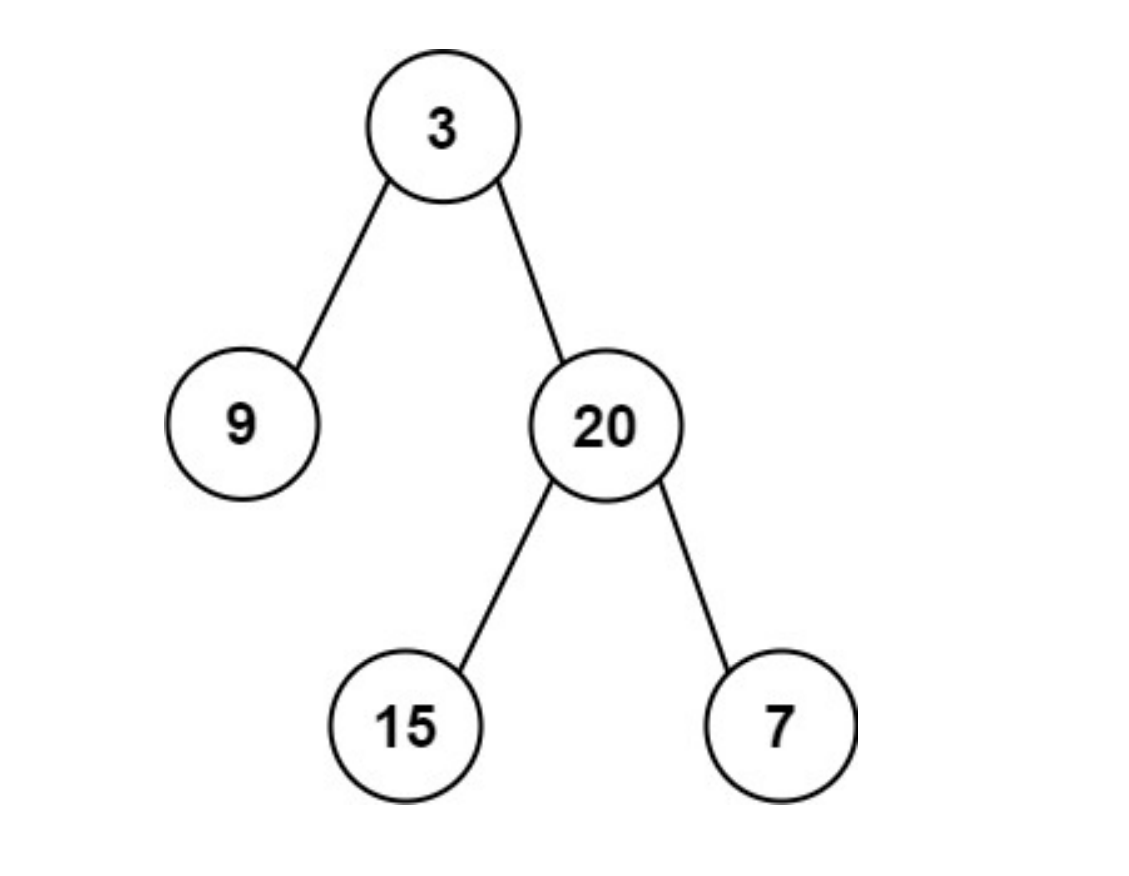
输入: [1,2,3,null,5,null,4]
输出: [1,3,4]
示例 2:
输入: [1,null,3]
输出: [1,3]
示例 3:
输入: []
输出: []
即利用队列的长度,把每一层的最后一个结点加入结果中
class Solution {public List<Integer> rightSideView(TreeNode root) {//即看到的都是每一层的最后一个结点List<Integer> ans =new ArrayList<>();Queue<TreeNode> queue =new LinkedList<>();if(root==null) return ans; //一定要判断为空的情况,否则会空指针异常queue.add(root);while(!queue.isEmpty()){int len =queue.size();while(len>0){TreeNode node =queue.poll();if(len==1) ans.add(node.val); //把每一层的最后一个结点加入if(node.left!=null)queue.add(node.left);if(node.right!=null)queue.add(node.right);len--;}}return ans;}
}
637、二叉树的层平均值
给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10-5 以内的答案可以被接受。
示例 1:
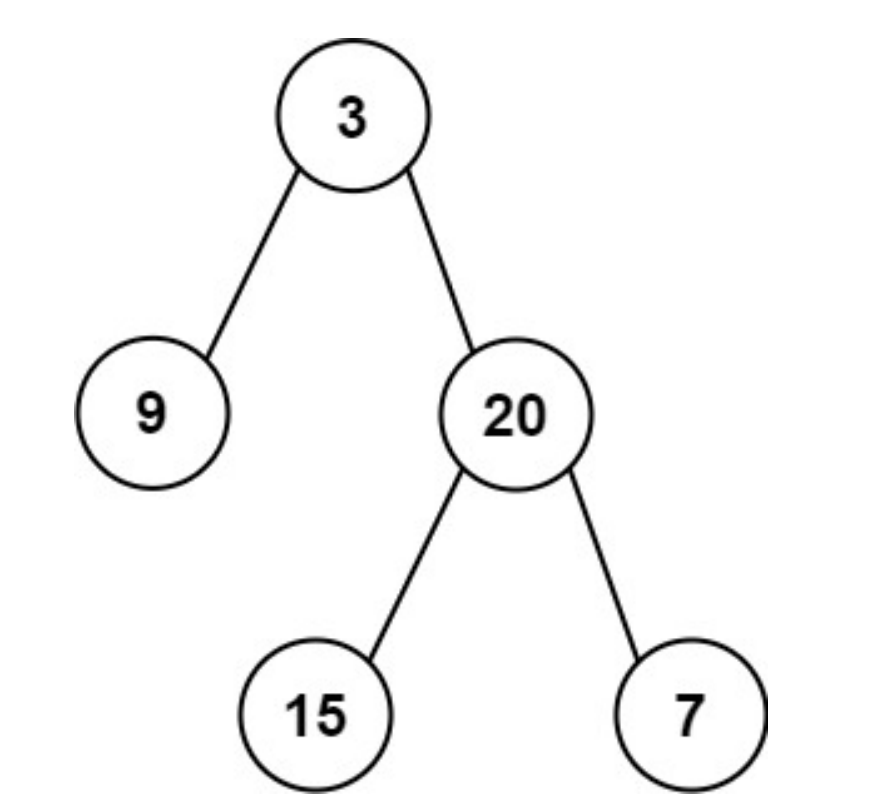
输入:root = [3,9,20,null,null,15,7]
输出:[3.00000,14.50000,11.00000]
解释:第 0 层的平均值为 3,第 1 层的平均值为 14.5,第 2 层的平均值为 11 。
因此返回 [3, 14.5, 11] 。
使用一个sum来计算每层的和
class Solution {public List<Double> averageOfLevels(TreeNode root) {List<Double> ans =new ArrayList<>();Queue<TreeNode> queue =new LinkedList<>();queue.add(root);while(!queue.isEmpty()){int len =queue.size();int n=len;double sum=0;while(len>0){TreeNode node =queue.poll();sum += node.val;if(node.left!=null)queue.add(node.left);if(node.right!=null)queue.add(node.right);len--;}ans.add(sum/n);}return ans;}
}
429、N叉树的层序遍历
给定一个 N 叉树,返回其节点值的层序遍历。(即从左到右,逐层遍历)。
树的序列化输入是用层序遍历,每组子节点都由 null 值分隔(参见示例)。
示例 1:
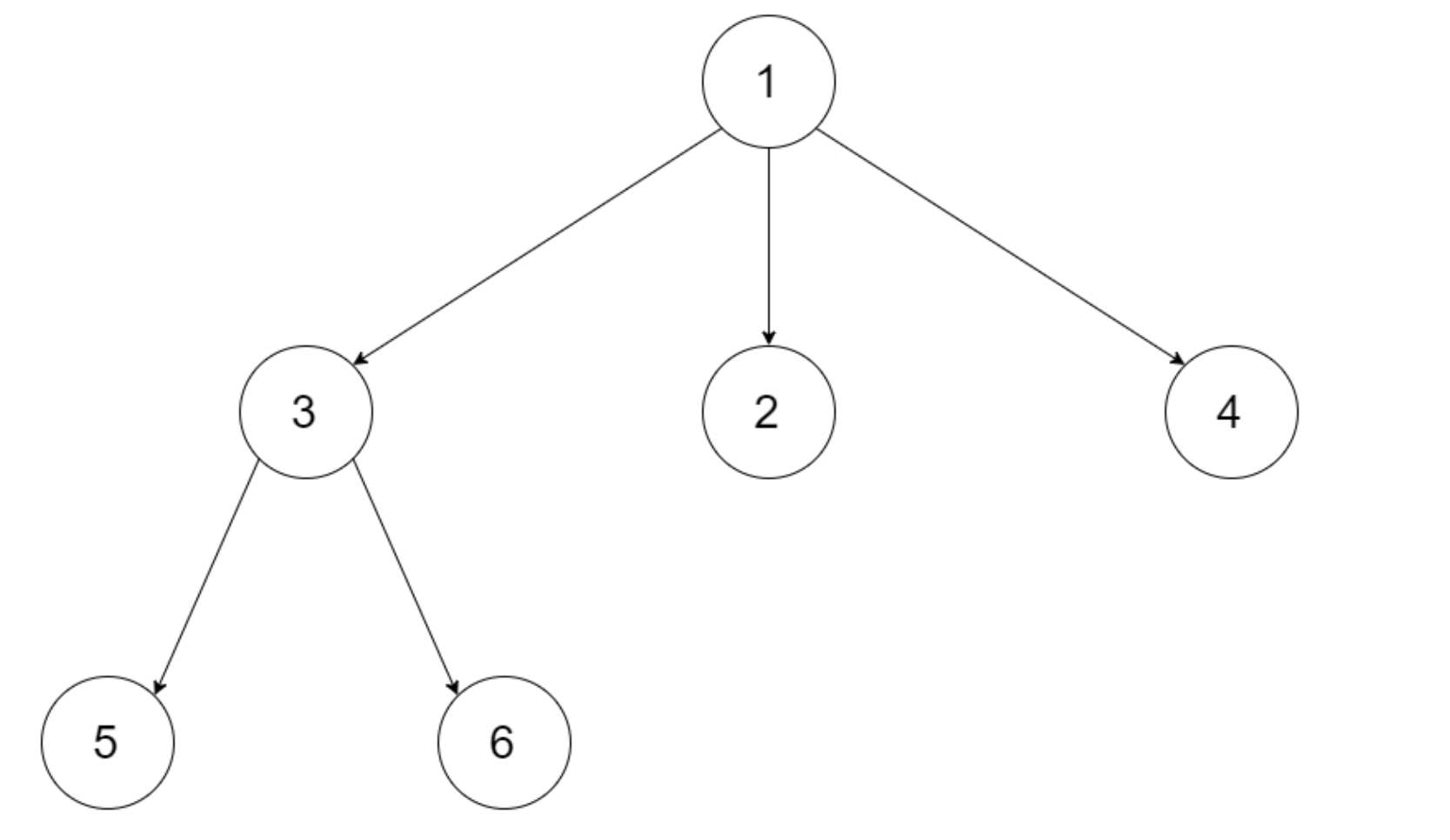
输入:root = [1,null,3,2,4,null,5,6]
输出:[[1],[3,2,4],[5,6]]
class Solution {public List<List<Integer>> levelOrder(Node root) {List<List<Integer>> ans= new ArrayList<List<Integer>>();Queue<Node> queue = new LinkedList<>();if(root==null) return ans;queue.add(root);while(!queue.isEmpty()){int len =queue.size();List<Integer> tmp=new ArrayList<>();while(len>0){Node node =queue.poll();tmp.add(node.val);len--;List<Node> childrens =node.children;for(Node c:childrens){if(c!=null) queue.add(c);}}ans.add(tmp);}return ans; }
}
515、找出每层的最大值
给定一棵二叉树的根节点 root ,请找出该二叉树中每一层的最大值。
示例1:
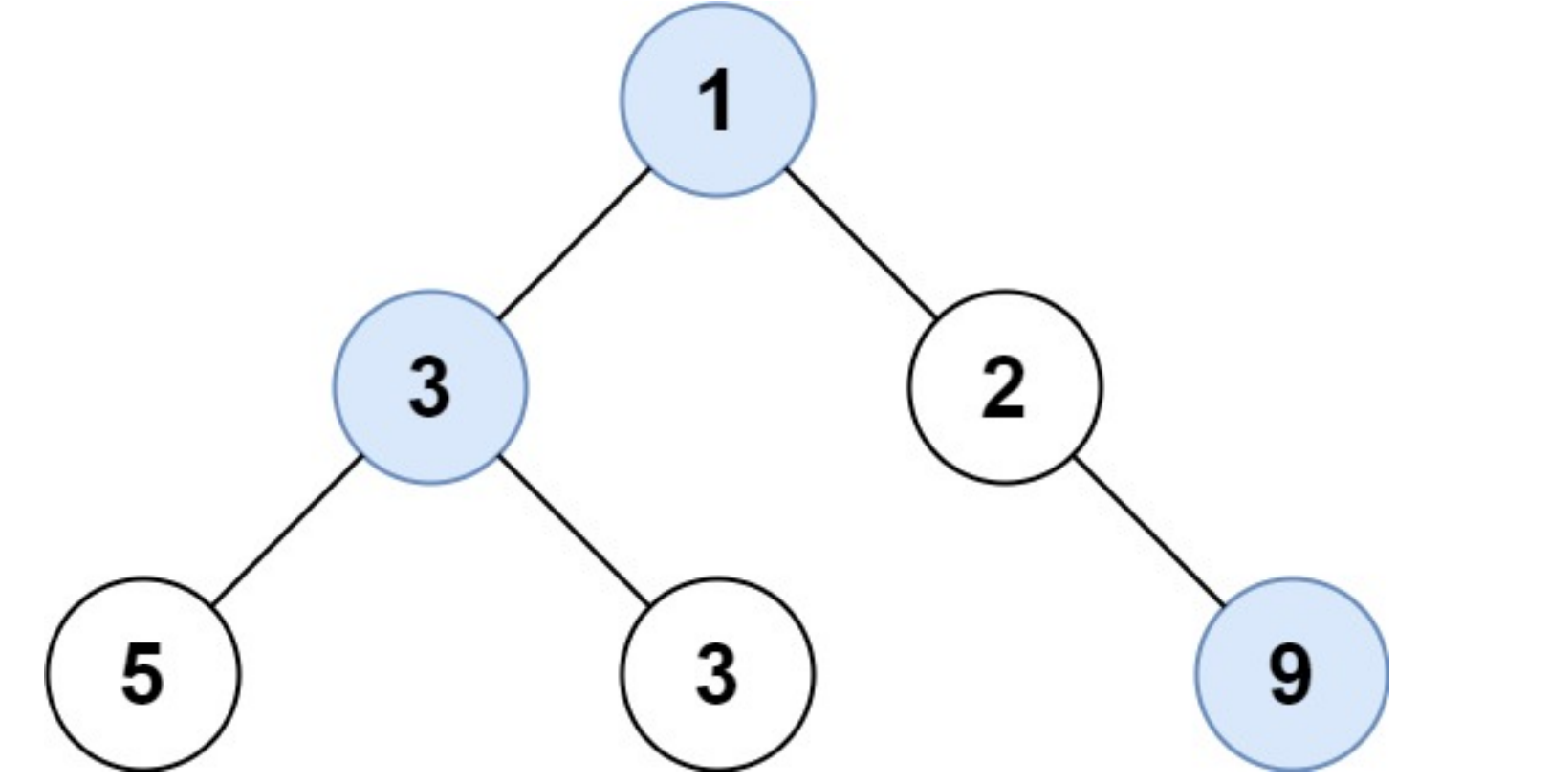
输入: root = [1,3,2,5,3,null,9]
输出: [1,3,9]
class Solution {public List<Integer> largestValues(TreeNode root) {List<Integer> ans =new ArrayList<>();if(root==null) return ans;Queue<TreeNode> queue =new LinkedList<>();queue.add(root);while(!queue.isEmpty()){int len =queue.size();int max=Integer.MIN_VALUE; //记录每一层的最大值while(len>0){TreeNode node = queue.poll();if(node.val>max)max=node.val;if(node.left!=null)queue.add(node.left);if(node.right!=null)queue.add(node.right);len--;}ans.add(max);}return ans;}
}
116、填充每个节点的下一个右侧节点指针
给定一个 完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
struct Node {int val;Node *left;Node *right;Node *next;
}
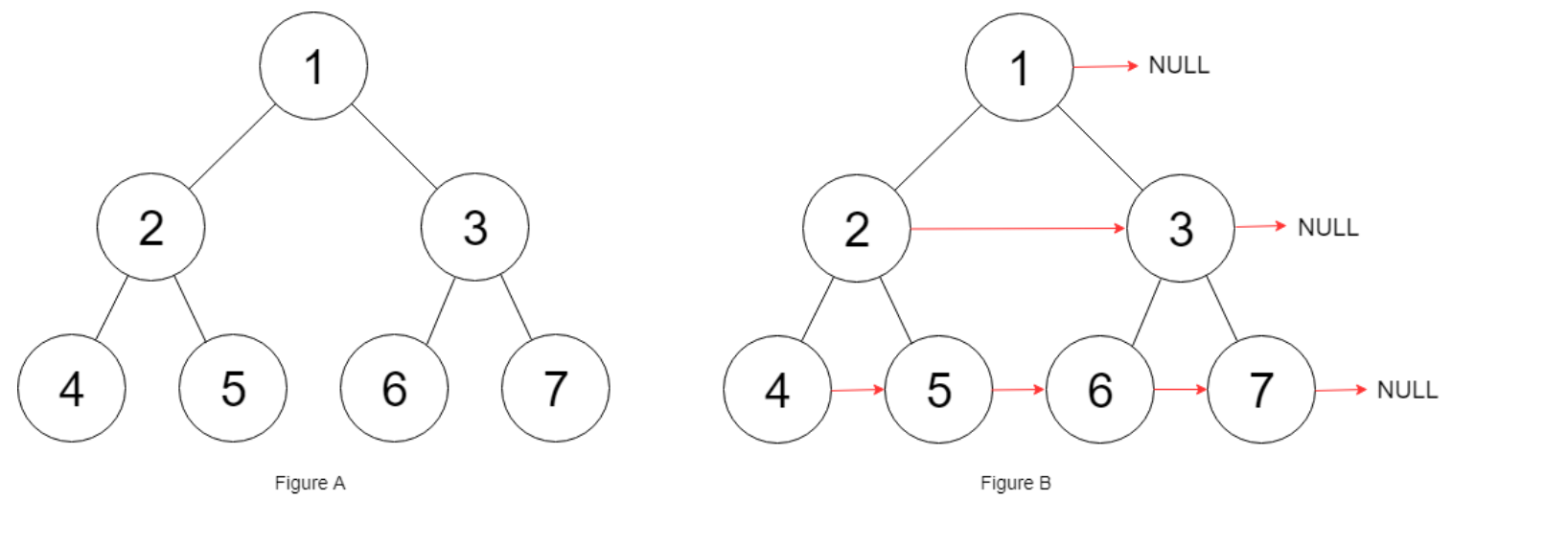
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
示例 1:
class Solution {public Node connect(Node root) {Queue<Node> queue =new LinkedList<>();if(root==null) return root;queue.add(root);while(!queue.isEmpty()){int len =queue.size();while(len>0){ Node node = queue.poll(); //本质上还是找到每层的最后一个结点if(len==1){node.next=null;}else{Node nextNode =queue.peek();node.next=nextNode;}len--;if(node.left!=null)queue.add(node.left);if(node.right!=null)queue.add(node.right);}}return root;}
}
#104、 二叉树的最大深度
使用前序求的就是深度,使用后序呢求的是高度
层序遍历:
class Solution {public int maxDepth(TreeNode root) {if(root==null) return 0;Queue<TreeNode> queue = new LinkedList<>();queue.add(root);int hight=0;while(!queue.isEmpty()){int len=queue.size();while(len>0){TreeNode node =queue.poll();if(node.left!=null)queue.add(node.left);if(node.right!=null)queue.add(node.right);len--;}hight++;}return hight;}
}
后续遍历:
class Solution {public int maxDepth(TreeNode root) {if(root==null) return 0;int leftDepth =maxDepth(root.left); //左int rightDepth =maxDepth(root.right); //右return Math.max(leftDepth,rightDepth)+1; //中}
}
前序遍历:
class Solution {public:int result;//使用result来记录最大深度void getDepth(TreeNode* node, int depth) {result = depth > result ? depth : result; // 中if (node->left == NULL && node->right == NULL) return ;if (node->left) { // 左getDepth(node->left, depth + 1);}if (node->right) { // 右getDepth(node->right, depth + 1);}return ;}int maxDepth(TreeNode* root) {result = 0;if (root == 0) return result;getDepth(root, 1);return result;}
};
101、 二叉树的最小深度
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
示例 1:
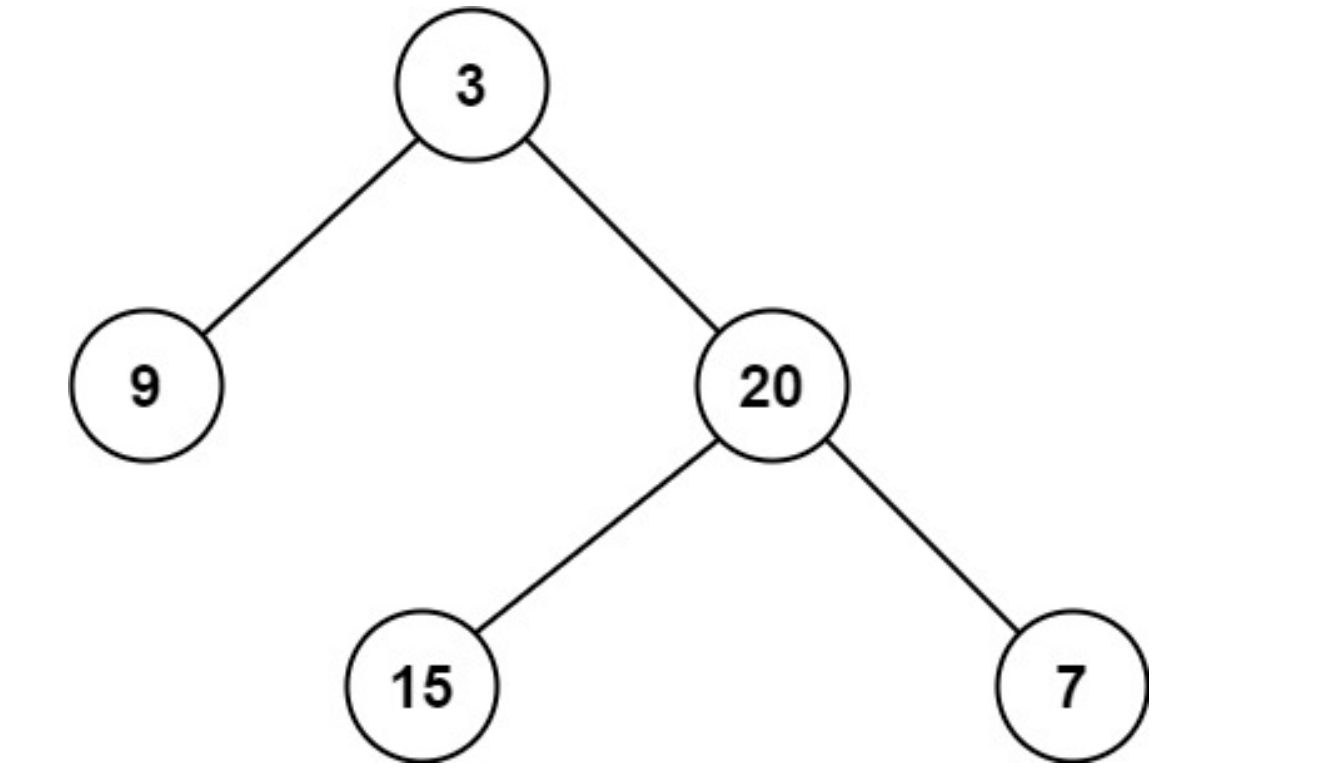
输入:root = [3,9,20,null,null,15,7]
输出:2
即当左右孩子都为空的时候就返回
层序遍历
class Solution {public int minDepth(TreeNode root) {if(root==null) return 0;Queue<TreeNode> queue = new LinkedList<>();queue.add(root);int depth=0;while(!queue.isEmpty()){int len=queue.size();depth++;while(len>0){TreeNode node =queue.poll();if(node.left!=null)queue.add(node.left);if(node.right!=null)queue.add(node.right);if(node.right==null && node.left==null)return depth;len--;}}return depth;}
}
递归法
如果左子树为空,右子树不为空,说明最小深度是 1 + 右子树的深度。
反之,右子树为空,左子树不为空,最小深度是 1 + 左子树的深度。 最后如果左右子树都不为空,返回左右子树深度最小值 + 1 。
class Solution {//递归法public int minDepth(TreeNode root) {if(root==null) return 0;int leftDepth = minDepth(root.left);int rightDepth = minDepth(root.right);if(root.left==null)return rightDepth+1; //否则没有左孩子的分支会被当成最小值if(root.right==null)return leftDepth+1;return Math.min(leftDepth,rightDepth)+1;}
}
#226、翻转二叉树
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
示例 1:
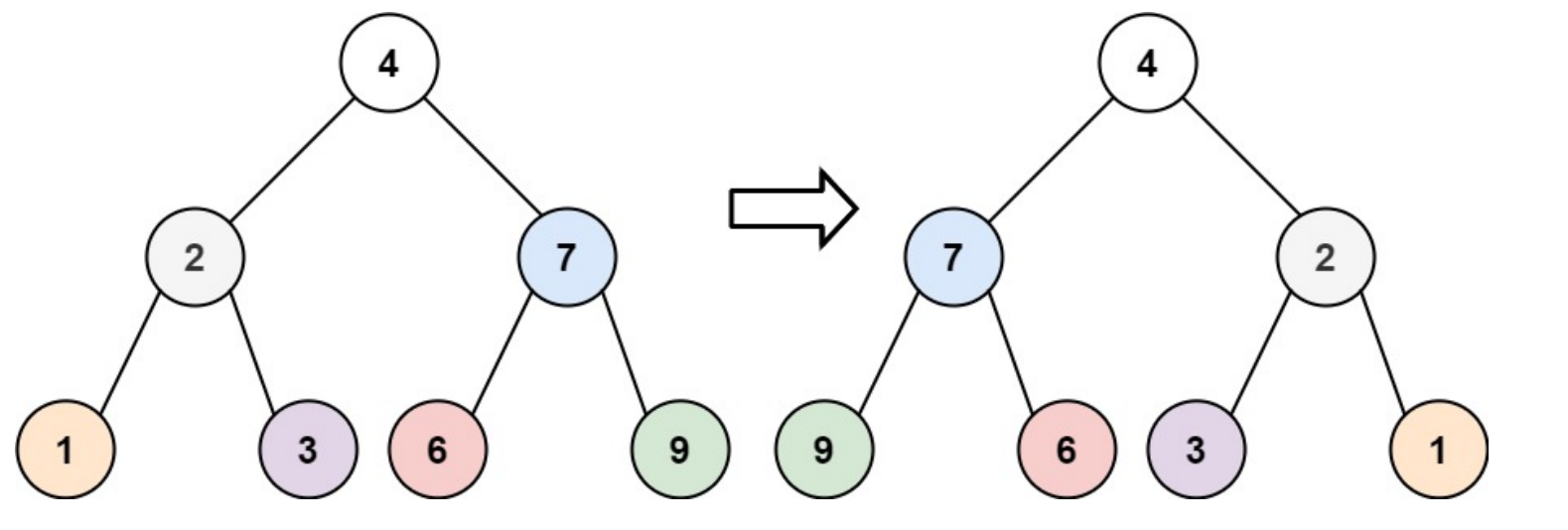
输入:root = [4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]
采用层序遍历,每取出一个结点就交换其左右孩子
class Solution {public TreeNode invertTree(TreeNode root) {//采用层序遍历Queue<TreeNode> queue =new LinkedList<>();if(root==null) return root;queue.add(root);while(!queue.isEmpty()){int len =queue.size();while(len>0){TreeNode node=queue.poll();TreeNode tmp =node.right;node.right=node.left;node.left=tmp;if(node.left!=null) queue.add(node.left);if(node.right!=null) queue.add(node.right);len--;}}return root;}
}
递归法:
对一个结点交换左右,然后进行左右递归
class Solution {/*** 前后序遍历都可以* 中序不行,因为先左孩子交换孩子,再根交换孩子(做完后,右孩子已经变成了原来的左孩子),再右孩子交换孩子(此时其实是对原来的左孩子做交换)*/public TreeNode invertTree(TreeNode root) {if (root == null) {return null;}invertTree(root.left);invertTree(root.right);swapChildren(root); //也可以中左右return root;}private void swapChildren(TreeNode root) {TreeNode tmp = root.left;root.left = root.right;root.right = tmp;}
}
#114、二叉树展开为链表
给你二叉树的根结点 root ,请你将它展开为一个单链表:
- 展开后的单链表应该同样使用 TreeNode ,其中 right 子指针指向链表中下一个结点,而左子指针始终为 null 。
- 展开后的单链表应该与二叉树 先序遍历 顺序相同。
示例 1:
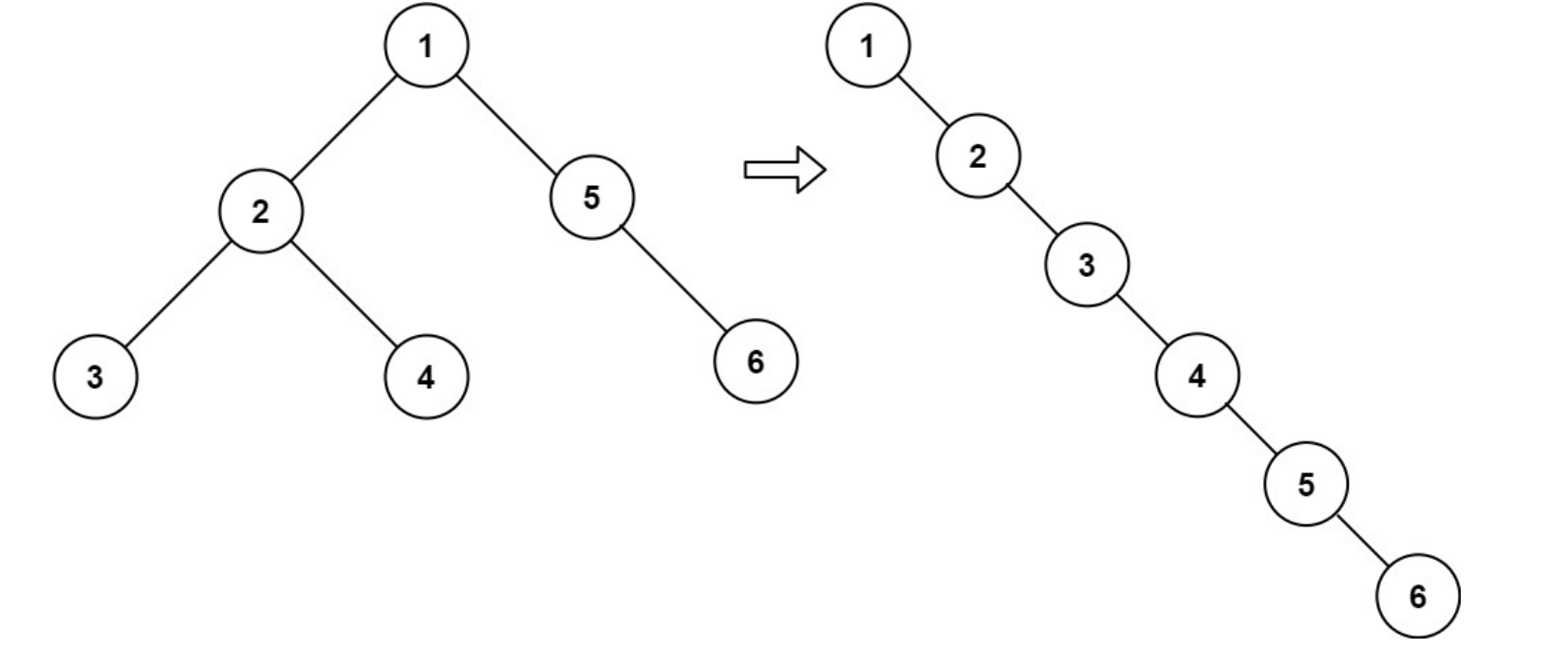
输入:root = [1,2,5,3,4,null,6]
输出:[1,null,2,null,3,null,4,null,5,null,6]
class Solution {//保存前序遍历的结果List<TreeNode> list=new ArrayList<>();public void flatten(TreeNode root) {preorder(root);for(int i=1;i<list.size();i++){TreeNode pre=list.get(i-1);TreeNode cur=list.get(i);pre.left=null;pre.right=cur;}}//构造树,然后值是结点public void preorder(TreeNode root){if(root==null)return;list.add(root);preorder(root.left);preorder(root.right);}
}
递归+回溯的思路,将前序遍历反过来遍历,那么第一次访问的就是前序遍历中最后一个节点。那么可以调整最后一个节点,再将最后一个节点保存到pre里,再调整倒数第二个节点,将它的右子树设置为pre,再调整倒数第三个节点,依次类推直到调整完毕。和反转链表的递归思路是一样的。
class Solution {//反前序遍历TreeNode pre;public void flatten(TreeNode root) {if(root==null)return;flatten(root.right);flatten(root.left);//先找到最后一个结点,然后记录root.left=null;root.right=pre;pre=root;}}
#101、对称二叉树
给你一个二叉树的根节点 root , 检查它是否轴对称。
示例 1:
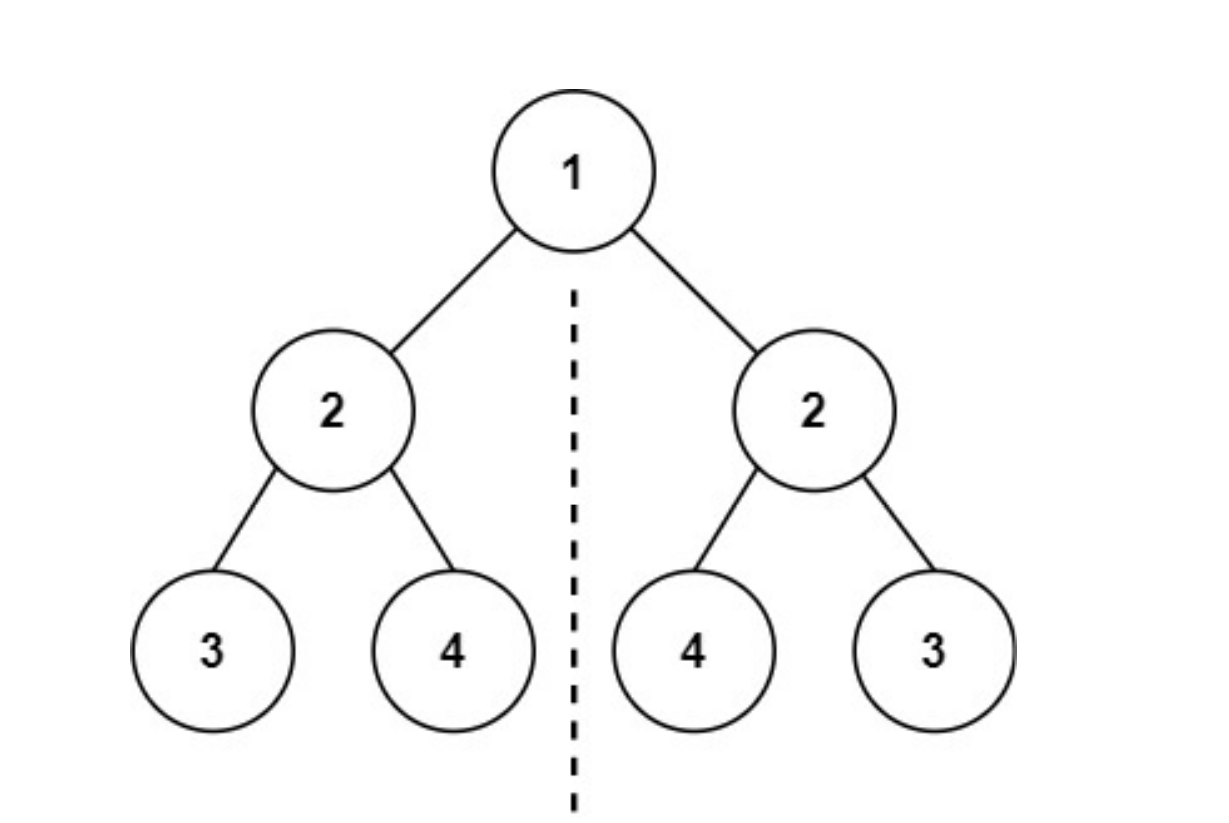
输入:root = [1,2,2,3,4,4,3]
输出:true
示例 2:

输入:root = [1,2,2,null,3,null,3]
输出:false
使用一个队列,类似于层序遍历的方式,只不过不用加len来判断层数,并且空结点也要入队。
而本题的迭代法中我们使用了队列,需要注意的是这不是层序遍历,而且仅仅通过一个容器来成对的存放我们要比较的元素,
class Solution {public boolean isSymmetric(TreeNode root) {//把空节点也看成结点Queue<TreeNode> queue =new LinkedList<>();queue.add(root.left);queue.add(root.right);while(!queue.isEmpty()){//不符合就返回falseTreeNode leftnode =queue.poll(); //每次取出需要比较的两个结点TreeNode rightnode =queue.poll(); //每次取出需要比较的两个结点if(leftnode==null && rightnode ==null)continue;if(leftnode==null||rightnode==null||leftnode.val!=rightnode.val)return false;queue.add(leftnode.left);queue.add(rightnode.right);queue.add(leftnode.right);queue.add(rightnode.left);}return true;}
}
递归法:
class Solution {private boolean copmare(TreeNode leftnode, TreeNode rightnode){if(leftnode==null && rightnode!=null) return false;else if(leftnode!=null && rightnode==null) return false;else if(leftnode==null && rightnode==null) return true;else if(leftnode.val!=rightnode.val) return false; //也可以合在一起判断else //说明leftnode和rightnode相等return copmare(leftnode.left,rightnode.right) && copmare(leftnode.right,rightnode.left);}public boolean isSymmetric(TreeNode root) {return copmare(root.left,root.right);}
}
100、相同的树
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
示例 1:
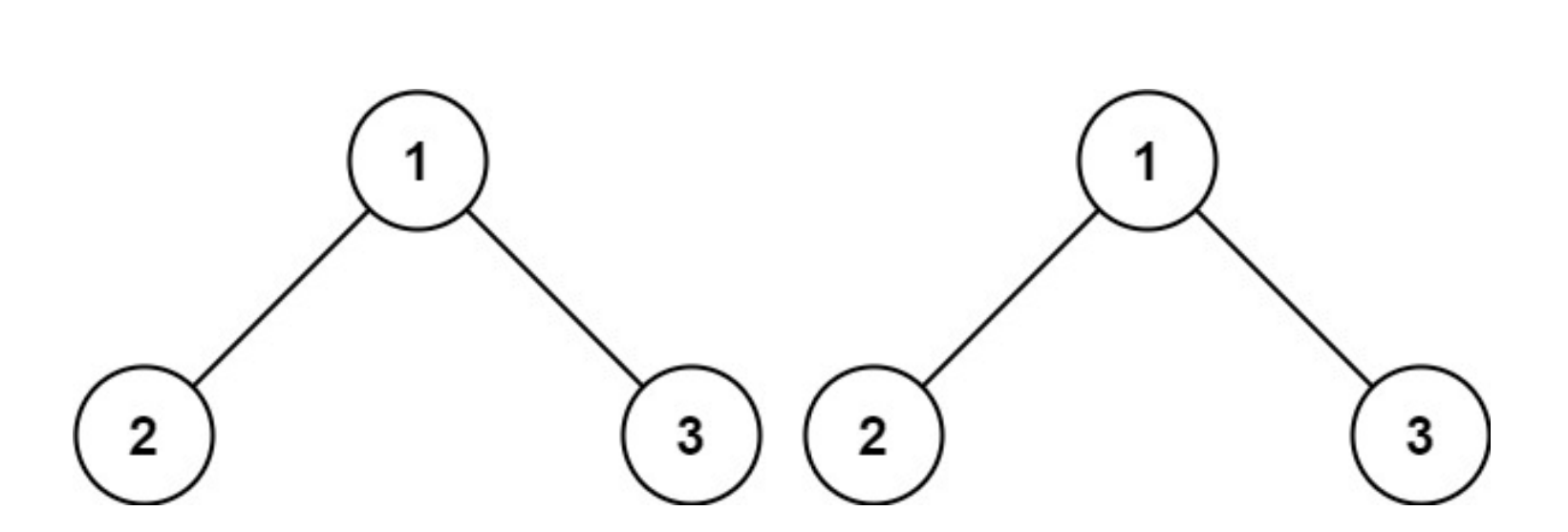
输入:p = [1,2,3], q = [1,2,3]
输出:true
和对称二叉树一样
class Solution {public boolean isSameTree(TreeNode p, TreeNode q) {//使用同一个队列Queue<TreeNode> queue =new LinkedList<>();queue.add(p);queue.add(q);while(!queue.isEmpty()){TreeNode node1 =queue.poll();TreeNode node2 =queue.poll();if(node1==null && node2==null)continue;else if(node1==null &&node2!=null)return false;else if(node1!=null && node2==null)return false;else if(node1.val!=node2.val)return false;queue.add(node1.left);queue.add(node2.left);queue.add(node1.right);queue.add(node2.right);}return true;}
}
递归法
class Solution {//递归法:求树是否相等public boolean isSameTree(TreeNode p, TreeNode q) {if(p==null&& q==null) return true;else if(p==null &&q!=null) return false;else if(p!=null &&q==null) return false;else if(p.val!=q.val) return false;else //即结点相同,判读左右结点{return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);}}
}
572、另一棵树的子树
给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在,返回 true ;否则,返回 false 。
二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。
示例 1:
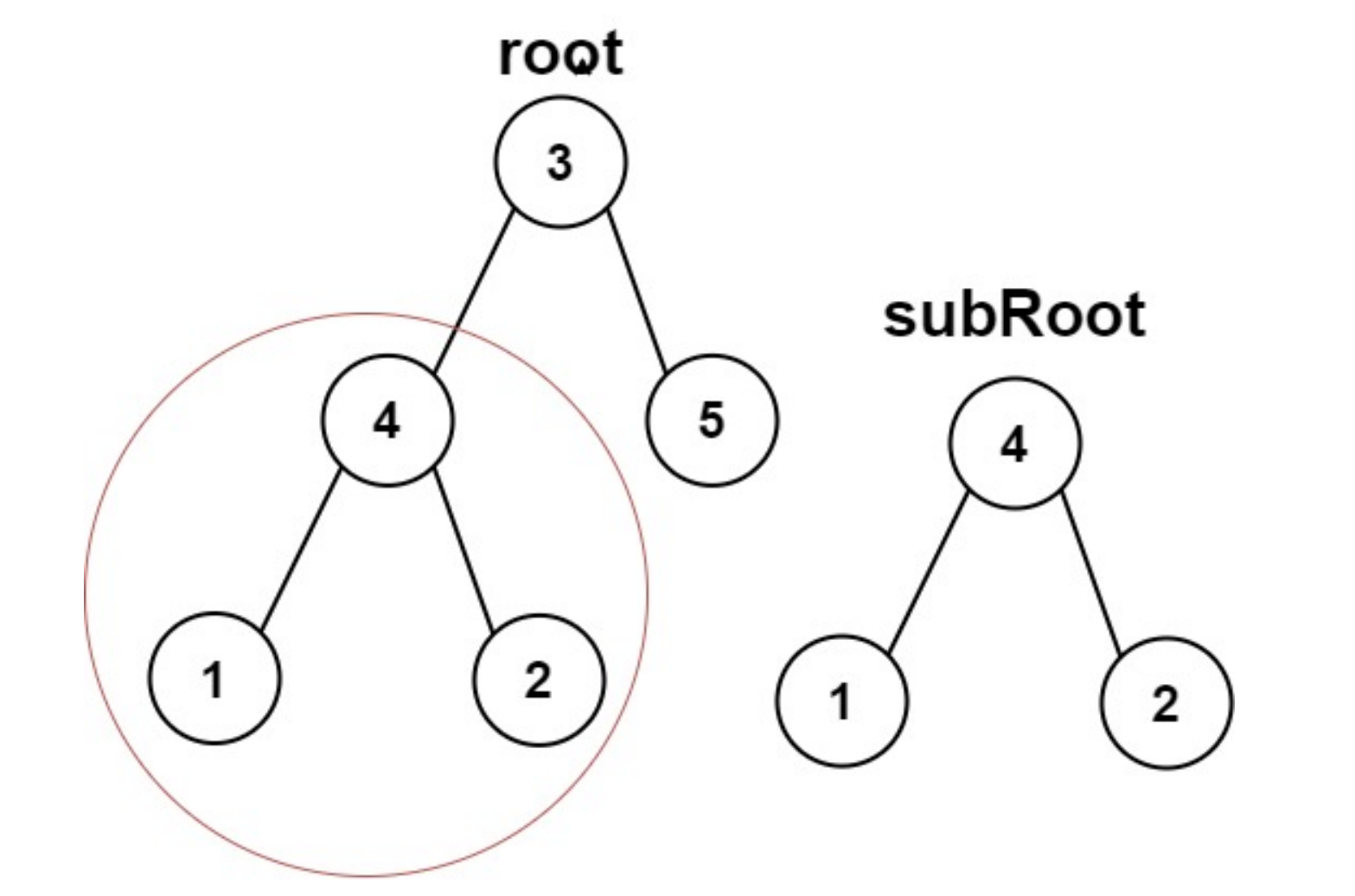
输入:root = [3,4,5,1,2], subRoot = [4,1,2]
输出:true
采用遍历+判断树是否相等
class Solution {public boolean isSameTree(TreeNode p, TreeNode q){if(p==null && q==null) return true;else if(p==null||q==null||p.val!=q.val) return false; //直接合在一起写else{ //说明结点值相同return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);}}public boolean isSubtree(TreeNode root, TreeNode subRoot) {Queue<TreeNode> queue =new LinkedList<>();queue.add(root);while(!queue.isEmpty()){TreeNode node =queue.poll();if(isSameTree(node,subRoot))return true;if(node.left!=null) queue.add(node.left);if(node.right!=null) queue.add(node.right);}return false;}
}
559、n叉树的最大深度
class Solution {/*递归法,后序遍历求root节点的高度*/public int maxDepth(Node root) {if (root == null) return 0; //递归出口int depth = 0;if (root.children != null){for (Node child : root.children){depth = Math.max(depth, maxDepth(child));}}return depth + 1; //中节点}
}
#110、平衡二叉树
在递归法求高度的基础上,每次递归要判断是否是平衡二叉树。
class Solution { //递归法求高度,因为是求高度,所以是后序遍历:左右中private int getHight(TreeNode root){if(root==null) return 0;int leftHight=getHight(root.left);if(leftHight==-1) return -1; //用-1代表不是平衡二叉树int rightHight=getHight(root.right);if(rightHight==-1) return -1;if(Math.abs(leftHight-rightHight)>1)return -1;return Math.max(leftHight,rightHight)+1;}public boolean isBalanced(TreeNode root) {if(getHight(root)==-1) return false;elsereturn true;}
}
层序遍历
class Solution { //层次遍历求高度private int getHigth(TreeNode root) {if(root==null) return 0;Queue<TreeNode> queue = new LinkedList<>();queue.add(root);int hight=0;while(!queue.isEmpty()){int len=queue.size();while(len>0){TreeNode node =queue.poll();if(node.left!=null)queue.add(node.left);if(node.right!=null)queue.add(node.right);len--;}hight++;}return hight;}//层次遍历判断public boolean isBalanced(TreeNode root) {if(root==null) return true;Queue<TreeNode> queue = new LinkedList<>();queue.add(root);while(!queue.isEmpty()){int len=queue.size();while(len>0){TreeNode node =queue.poll();int leftHight =getHigth(node.left);int rightHight =getHigth(node.right);if(Math.abs(leftHight-rightHight)>1)return false;if(node.left!=null)queue.add(node.left);if(node.right!=null)queue.add(node.right);len--;}}return true;}
}
#543、二叉树的直径
给你一棵二叉树的根节点,返回该树的 直径 。
二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。
两节点之间路径的 长度 由它们之间边数表示。
示例 1:
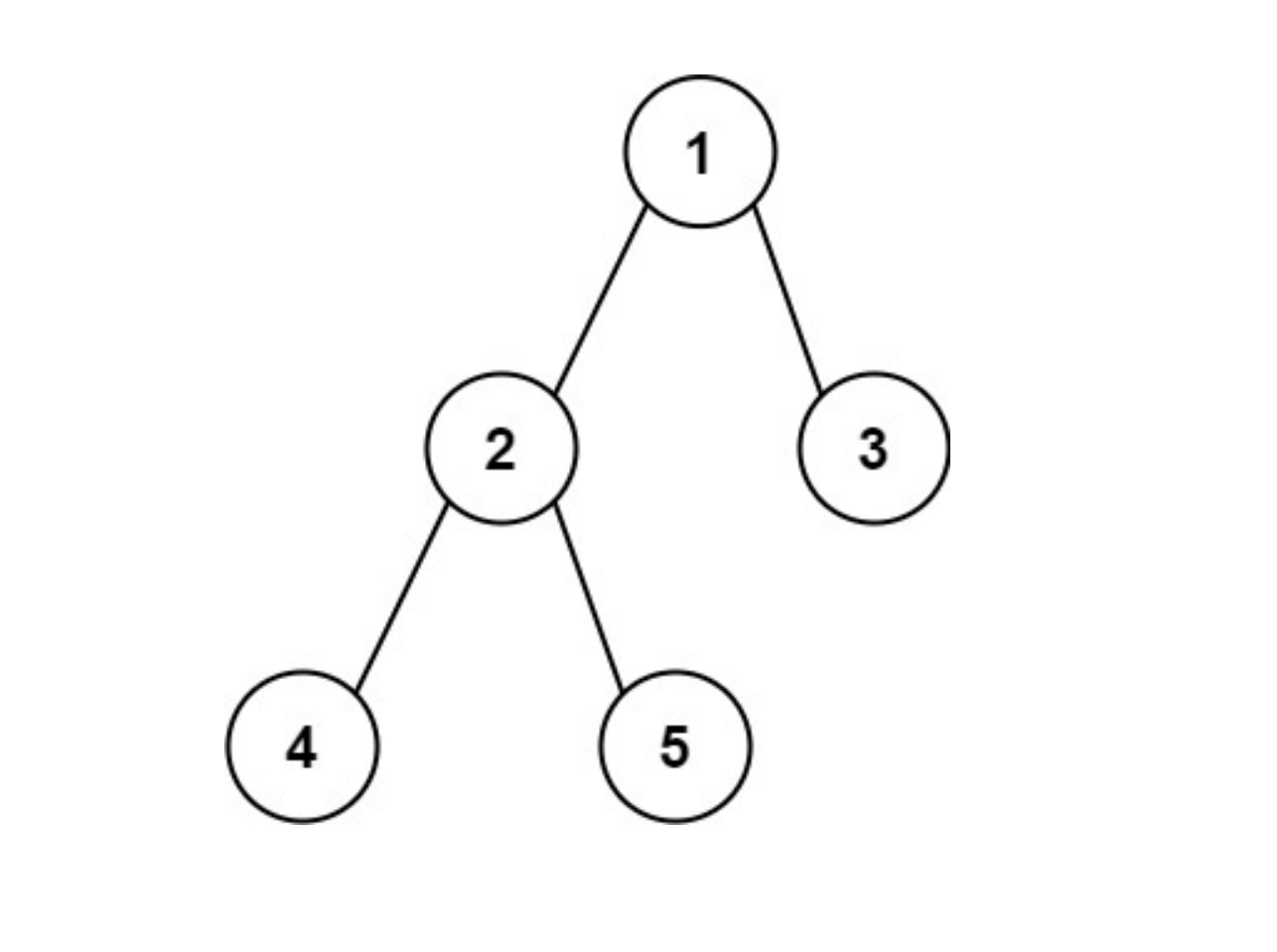
输入:root = [1,2,3,4,5]
输出:3
解释:3 ,取路径 [4,2,1,3] 或 [5,2,1,3] 的长度。
示例 2:
输入:root = [1,2]
输出:1
一开始以为就是根节点的左右子树的深度之和,后来发现最长路径不一定经过根结点。
class Solution {//直径,即树中找最长路径,最长路径不一定经过根结点//对于经过的每一个结点来说,最长路径就是左右子树的深度 之和int maxd=0; //记录最大直径public int diameterOfBinaryTree(TreeNode root) {height(root);return maxd; }//递归求深度public int height(TreeNode root){if(root==null)return 0;int left=height(root.left);int right=height(root.right);//在遍历的过程中找以每个结点为根的最大直径maxd=Math.max(maxd,left+right); //将每个节点最大直径(左子树深度+右子树深度)当前最大值比较并取大者return Math.max(left,right)+1; //返回结点深度}
}
相关文章:

算法题总结(十)——二叉树上
#二叉树的递归遍历 // 前序遍历递归LC144_二叉树的前序遍历 class Solution {public List<Integer> preorderTraversal(TreeNode root) {List<Integer> result new ArrayList<Integer>(); //也可以把result 作为全局变量,只需要一个函数即可。…...

【MySQL】MySQL 数据库主从复制详解
目录 1. 基本概念1.1 主从架构1.2 复制类型 2. 工作原理2.1 复制过程2.2 主要组件 3. 配置步骤3.1 准备工作3.2 在主服务器上配置3.3 在从服务器上配置 4. 监控和维护4.1 监控复制状态4.2 处理复制延迟4.3 故障恢复 5. 备份策略5.1 逻辑备份与物理备份5.2 增量备份 6. 使用场景…...

一种格式化printf hex 数据的方法
格式化输出HEX数据 调试过程中通常需要个格式化输出16进制数据,为了方便美观可以参考如下方法。 #define __is_print(ch) ((unsigned int)((ch) - ) < 127u - )/*** dump_hex* * brief hex打印* * param buf: 需要打印的原始数据* param size: 原始数据类型*…...
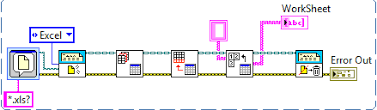
在LabVIEW中如何读取EXCEL
在LabVIEW中读取Excel文件通常使用“报告生成工具包”(Report Generation Toolkit)。以下是详细步骤: 安装工具包:确保已安装“报告生成工具包”。这通常随LabVIEW一起提供,但需要单独安装。 创建VI: 打…...

布匹瑕疵检测数据集 4类 2800张 布料缺陷 带标注 voc yolo
布匹瑕疵检测数据集 4类 2800张 布料缺陷 带标注 voc yolo 对应标注,格式VOC (XML),选配Y0L0(TXT) label| pic_ num| box_ _num hole: (425, 481) suspension_ wire: (1739, 1782) topbasi: (46, 46) dirty: (613&…...

灵动微高集成度电机MCU单片机
由于锂电技术的持续进步、消费者需求的演变、工具种类的革新以及应用领域的扩展,电动工具行业正呈现出无绳化、锂电化、大功率化、小型化、智能化和一机多能化的发展趋势。无绳化和锂电化的电动工具因其便携性和高效能的特性,已成为市场增长的重要驱动力…...

陪护小程序|护理陪护系统|陪护小程序成品
智能化,作为智慧医疗宏伟蓝图的基石,正引领着一场医疗服务的深刻变革。在这场变革的浪潮中,智慧医院小程序犹如璀璨新星,迅速崛起,而陪护小程序的诞生,更是如春风化雨,细腻地触及了老年病患、家…...

【JVM】基础篇
1 初识JVM 1.1 什么是JVM JVM 全称是 Java Virtual Machine,中文译名 Java虚拟机。JVM 本质上是一个运行在计算机上的程序,他的职责是运行Java字节码文件。 Java源代码执行流程如下: 分为三个步骤: 1、编写Java源代码文件。 …...

软件测试工程师 朝哪里进阶?
软件测试工程师 朝哪里进阶? 这里浅谈一下我的看法。 软件测试工程师 朝哪里进阶呢? 当我们测试工程师工作了2-3年后,就需要往前走往高走,就像一句名言说的:我们需要像ceo一样工作。 将自己的边界扩大一点࿰…...

Obsidian Plugin Release Pre-check
- [ ] 修改代码 - [ ] 修改README.md - [ ] 修改manifest.json - [ ] --将上述修改push到GitHub-- - [ ] 修改release版本 git tag git tag -a 1.0.6 -m "1.0.6" git push origin 1.0.6 ------------------------------------------- 备忘https://semver.org/lang/…...

Unity中实现预制体自动巡逻与攻击敌人的完整实现指南
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

OpenJudge | Shortest Prefixes
总时间限制: 1000ms 内存限制: 65536kB 描述 A prefix of a string is a substring starting at the beginning of the given string. The prefixes of “carbon” are: “c”, “ca”, “car”, “carb”, “carbo”, and “carbon”. Note that the empty string is not co…...

速盾:高防服务器是如何防御CC攻击的?
高防服务器是一种专门用于防御DDoS(分布式拒绝服务)攻击的服务器。其中一种常见的DDoS攻击就是CC(连续性攻击),它通过向目标服务器发送大量的请求来耗尽服务器资源,使网站无法正常运行。高防服务器采用多种…...

Android阶段学习思维导图
前言 记录下自己做的一个对Android原生应用层的思维导图,方便个人记忆扩展;这里只露出二级标题。 后语 虽然有些内容只是初步了解,但还是记录了下来;算是对过去一段学习的告别。...

React生命周期案例详解
React 组件的生命周期是指组件从创建、渲染、更新到卸载的整个过程。在 React 16 及之前的版本中,生命周期方法被分为几个不同的阶段:挂载(Mounting)、更新(Updating)、卸载(Unmounting…...

【ubuntu】ubuntu20.04安装显卡驱动
1.安装 点击右下角Apply Changes。 等安装好之后,重启。 现在的nvidia驱动已经很好安装了,比早期时安装出现黑屏等情况好了很多。 2.验证 nvidia-smi...

Mongo Java Driver使用getCollection做分页查询遇到的一些坑
背景 最近在做Mongo上的表数据的迁移,原本应该是DBA要干的活,但是想着DBA排期比较长,加上我们开发的权限又非常有限,而且数据量又没有多少,就想着自己开发个小小的程序从旧实例上查,写到新实例上去算了。于…...

RK3568笔记六十四:SG90驱动测试
若该文为原创文章,转载请注明原文出处。 前面有测试过PWM驱动,现在使用两种方式来产生PWM驱动SG90,实现舵机旋转任意角度 方法一:使用硬件PWM 方法二:使用高精度定时器,GPIO模拟PWM. 一、PWM子系统框架 二、SG90控制方法 舵机的控制需要MCU产生一个周期为20ms的脉冲信号…...
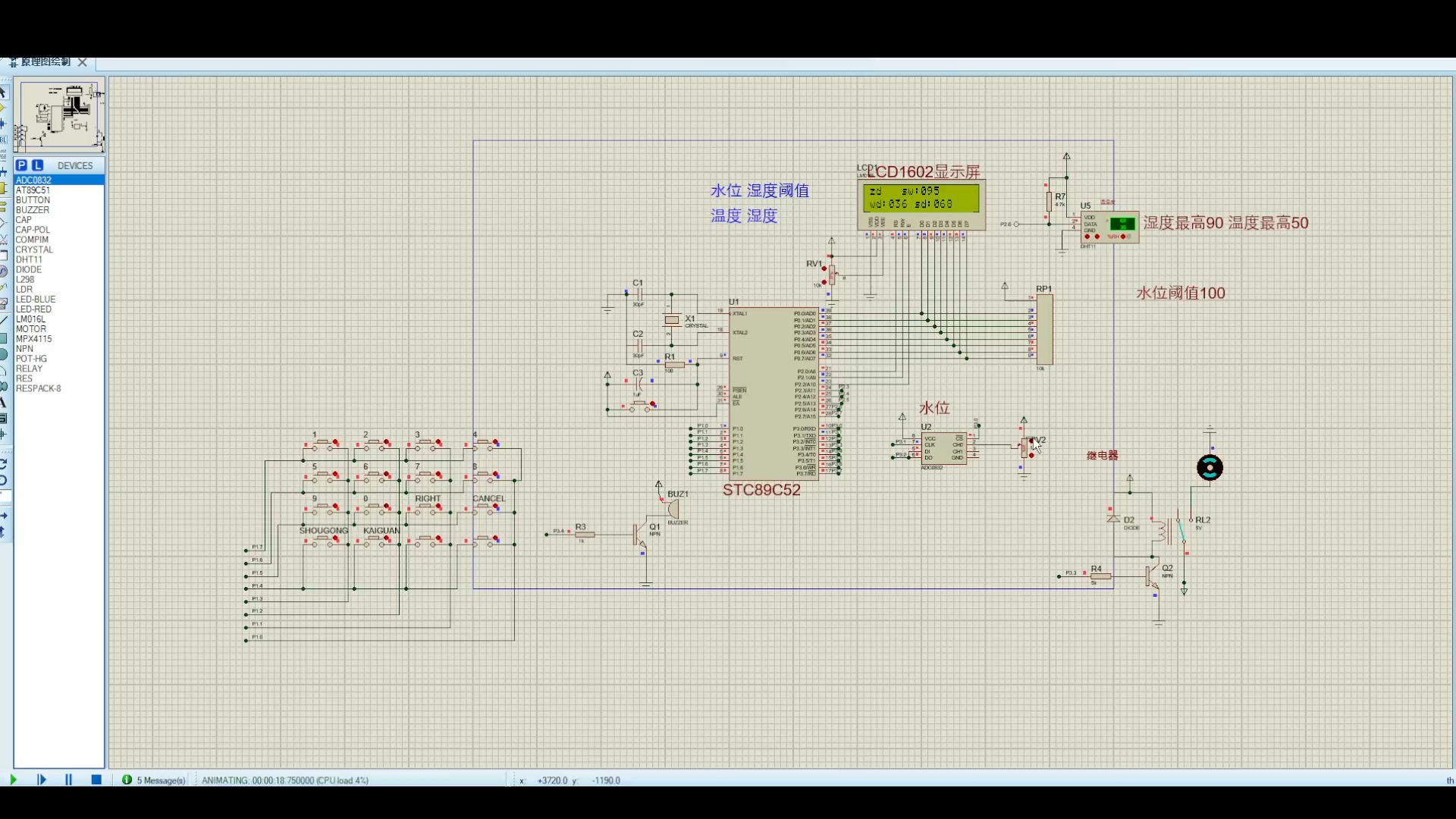
31 基于51单片机的水位监测系统仿真
目录 一、主要功能 二、硬件资源 三、程序编程 四、实现现象 一、主要功能 基于51单片机,DHT11温湿度检测,水位检测,通过LCD1602显示,超过阈值报警,继电器驱动电机转动。通过矩阵按键切换选择设置各项参数阈值。 …...

Docker 实践与应用举例
一、容器化Web应用: 创建一个Docker容器来运行一个简单的Web应用,例如一个基于Node.js的Express应用。首先,编写Dockerfile来定义容器的构建过程,然后使用Docker命令来构建和运行容器。 使用Docker Compose来定义和管理多个容器组…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...
