【AI知识点】梯度消失(Vanishing Gradient)和梯度爆炸(Exploding Gradient)
梯度消失(Vanishing Gradient) 和梯度爆炸(Exploding Gradient) 是神经网络训练中的常见问题,特别是在深层神经网络(DNN)或递归神经网络(RNN)中。这两者主要与反向传播算法中的梯度计算有关,它们会导致模型在训练过程中收敛困难,甚至无法正确学习。
1. 梯度消失(Vanishing Gradient)
a. 定义
梯度消失问题是指在训练深层神经网络时,随着网络层数的增加,反向传播过程中早期层(靠近输入层)的梯度逐渐接近于零,导致这些层的参数几乎无法更新。这样,网络中的某些参数将无法被有效学习,模型训练停滞不前。
b. 数学解释
在神经网络中,反向传播算法用于通过链式法则(Chain Rule)计算损失函数相对于网络中每一层权重的偏导数。在深层网络中,链式法则会不断地乘以每一层的激活函数的导数。如果激活函数的导数非常小(小于 1),随着层数增加,梯度会逐层缩小。
对于每一层 l l l,反向传播的梯度计算公式为:
∂ L ∂ W [ l ] = ∂ L ∂ z [ l ] ⋅ ∂ z [ l ] ∂ W [ l ] \frac{\partial \mathcal{L}}{\partial W^{[l]}} = \frac{\partial \mathcal{L}}{\partial z^{[l]}} \cdot \frac{\partial z^{[l]}}{\partial W^{[l]}} ∂W[l]∂L=∂z[l]∂L⋅∂W[l]∂z[l]
如果层数很多,那么 ∂ L ∂ z [ l ] \frac{\partial \mathcal{L}}{\partial z^{[l]}} ∂z[l]∂L 中的每一项都会涉及前一层的梯度,最终导致梯度的乘积在反向传播过程中逐渐变小。这样在靠近输入层时,梯度几乎为 0,参数更新幅度极小,导致网络的训练效率大大降低,甚至无法训练。
c. 常见原因
-
激活函数问题:某些常用的激活函数(如 Sigmoid 和 Tanh)在输入值较大或较小时,它们的导数趋近于零,导致梯度在反向传播过程中缩小。例如:
- 对于 Sigmoid 函数:
Sigmoid ( z ) = 1 1 + e − z \text{Sigmoid}(z) = \frac{1}{1 + e^{-z}} Sigmoid(z)=1+e−z1
其导数:
d d z Sigmoid ( z ) = Sigmoid ( z ) ⋅ ( 1 − Sigmoid ( z ) ) \frac{d}{dz} \text{Sigmoid}(z) = \text{Sigmoid}(z) \cdot (1 - \text{Sigmoid}(z)) dzdSigmoid(z)=Sigmoid(z)⋅(1−Sigmoid(z))
当 z z z 非常大或非常小时,导数接近 0。
- 对于 Sigmoid 函数:
-
深度网络结构:网络层数越深,梯度乘积的次数越多,梯度消失的风险越大。
d. 梯度消失的影响
- 网络中的靠近输入层的权重更新非常缓慢甚至几乎不更新,导致这些层在训练中无法学习有效的表示。
- 网络的训练效率降低,模型很难收敛,特别是在处理复杂的任务时效果不佳。
e. 解决方法
-
使用合适的激活函数:
- ReLU(Rectified Linear Unit):ReLU 是一种在正值区域保持线性,而在负值区域输出为零的激活函数。它的导数在正区间为 1,因此能有效缓解梯度消失问题:
ReLU ( x ) = max ( 0 , x ) \text{ReLU}(x) = \max(0, x) ReLU(x)=max(0,x)
它的导数为:
d d x ReLU ( x ) = { 1 if x > 0 0 if x ≤ 0 \frac{d}{dx} \text{ReLU}(x) = \begin{cases} 1 & \text{if } x > 0 \\ 0 & \text{if } x \leq 0 \end{cases} dxdReLU(x)={10if x>0if x≤0 - 其他变种激活函数(如 Leaky ReLU、ELU)也能有效缓解梯度消失问题。
- ReLU(Rectified Linear Unit):ReLU 是一种在正值区域保持线性,而在负值区域输出为零的激活函数。它的导数在正区间为 1,因此能有效缓解梯度消失问题:
-
使用残差网络(ResNet):
- 残差网络(ResNet) 通过引入跳跃连接(Skip Connections),允许梯度在反向传播过程中绕过一些层,缓解了梯度消失问题。
-
批归一化(Batch Normalization):
- Batch Normalization 通过在每一层归一化激活值,使得输出的分布更加稳定,从而减少了梯度消失的发生。
2. 梯度爆炸(Exploding Gradient)
a. 定义
梯度爆炸是指在训练深层神经网络时,反向传播过程中梯度变得非常大,导致参数更新的幅度过大,最终导致模型的权重值溢出,损失函数出现异常情况(如 NaN),模型无法收敛。
b. 数学解释
梯度爆炸的问题与梯度消失相反。如果反向传播过程中每一层的梯度都大于 1,那么在链式法则的作用下,梯度会不断累积放大,最终导致前几层的梯度值过大,导致参数更新幅度过大,甚至可能使权重变得非常大。
在深层网络中,每层梯度的乘积计算公式为:
∂ L ∂ W [ l ] = ∂ L ∂ z [ l ] ⋅ ∂ z [ l ] ∂ W [ l ] \frac{\partial \mathcal{L}}{\partial W^{[l]}} = \frac{\partial \mathcal{L}}{\partial z^{[l]}} \cdot \frac{\partial z^{[l]}}{\partial W^{[l]}} ∂W[l]∂L=∂z[l]∂L⋅∂W[l]∂z[l]
如果梯度 ∂ L ∂ z [ l ] \frac{\partial \mathcal{L}}{\partial z^{[l]}} ∂z[l]∂L 的值非常大,那么靠近输入层的梯度将迅速增长,导致梯度爆炸。
c. 常见原因
-
权重初始化不当:如果网络的权重初始化得过大,那么在反向传播中,梯度的值可能会不断放大,导致梯度爆炸。
-
学习率过大:如果学习率设置过高,那么每次梯度更新的步长就会过大,导致权重迅速变大,引发梯度爆炸。
-
深度网络结构:在非常深的网络中,累积的梯度可能会迅速增大,导致前几层梯度的指数式增长。
d. 梯度爆炸的影响
- 梯度过大导致网络的权重更新幅度过大,网络的训练变得不稳定,甚至导致权重值溢出。
- 损失函数可能出现 NaN(非数值),训练中止或模型无法收敛。
e. 解决方法
-
梯度裁剪(Gradient Clipping):
- 梯度裁剪 是一种常用的方法,在每次反向传播时,如果梯度的值超过了某个阈值,就将其裁剪到该阈值范围内,防止梯度过大。这样可以有效避免梯度爆炸。
-
权重初始化:
- 使用适当的权重初始化方法可以避免梯度爆炸。常见的初始化方法包括:
- Xavier 初始化:适用于 Sigmoid 和 Tanh 激活函数,保持权重的方差在每一层中保持平衡。
- He 初始化:适用于 ReLU 激活函数,它通过缩小初始权重范围减少梯度爆炸的可能性。
- 使用适当的权重初始化方法可以避免梯度爆炸。常见的初始化方法包括:
-
降低学习率:
- 如果学习率过高,可以适当调低学习率,使梯度更新时的步长减小,减少爆炸的可能性。
-
使用批归一化(Batch Normalization):
- 批归一化 也可以缓解梯度爆炸。它在每一层对激活值进行标准化,防止输出值过大,从而限制了梯度的增大。
相关文章:
和梯度爆炸(Exploding Gradient))
【AI知识点】梯度消失(Vanishing Gradient)和梯度爆炸(Exploding Gradient)
梯度消失(Vanishing Gradient) 和梯度爆炸(Exploding Gradient) 是神经网络训练中的常见问题,特别是在深层神经网络(DNN)或递归神经网络(RNN)中。这两者主要与反向传播算…...

在 ArkTS 网络请求中,重新封装一下 http 模块
在ArkTS中,重新封装http模块可以提供一个更简洁、更易于使用的API,同时隐藏底层细节,使开发者能够更专注于业务逻辑。以下是一个简单的示例,展示了如何重新封装鸿蒙系统的kit.NetworkKit中的http模块: // 创建一个新的…...

Microsoft 更新 Copilot AI,未來將能使用語音並看到你瀏覽的網頁
不過受到 Recall 事件的影響,更新的推出將更緩慢謹慎。 Microsoft 也同步對其網頁版及行動版的 Copilot AI 進行大改版。這主要是為網頁版換上了一個較為簡單乾淨的介面,並增加了一些新的功能,像是 Copilot Voice 能讓你與 AI 助手進行對話式…...

系统架构设计师-论文题(2021年下半年)
1.试题一 论面向方面的编程技术及其应用针对应用开发所面临的规模不断扩大、复杂度不断提升的问题,面向方面的编程Aspect Oriented Programming,AOP技术提供了一种有效的程序开发方法。为了理解和完成一个复杂的程序,通常要把程序进行功能划分和封装。一…...

selenium的webdriver常用方法和属性介绍(2)
selenium的webdriver介绍 从selenium导入webdriver模块,在pycharm中跳转webdriver模块的__init__.py文件,内容如图所示:从selenium包的子目录中导入了很多模块并做了重命名,用于支持如下 Chrome/Edge/Ie/Firefox/Safari浏览器。 使…...
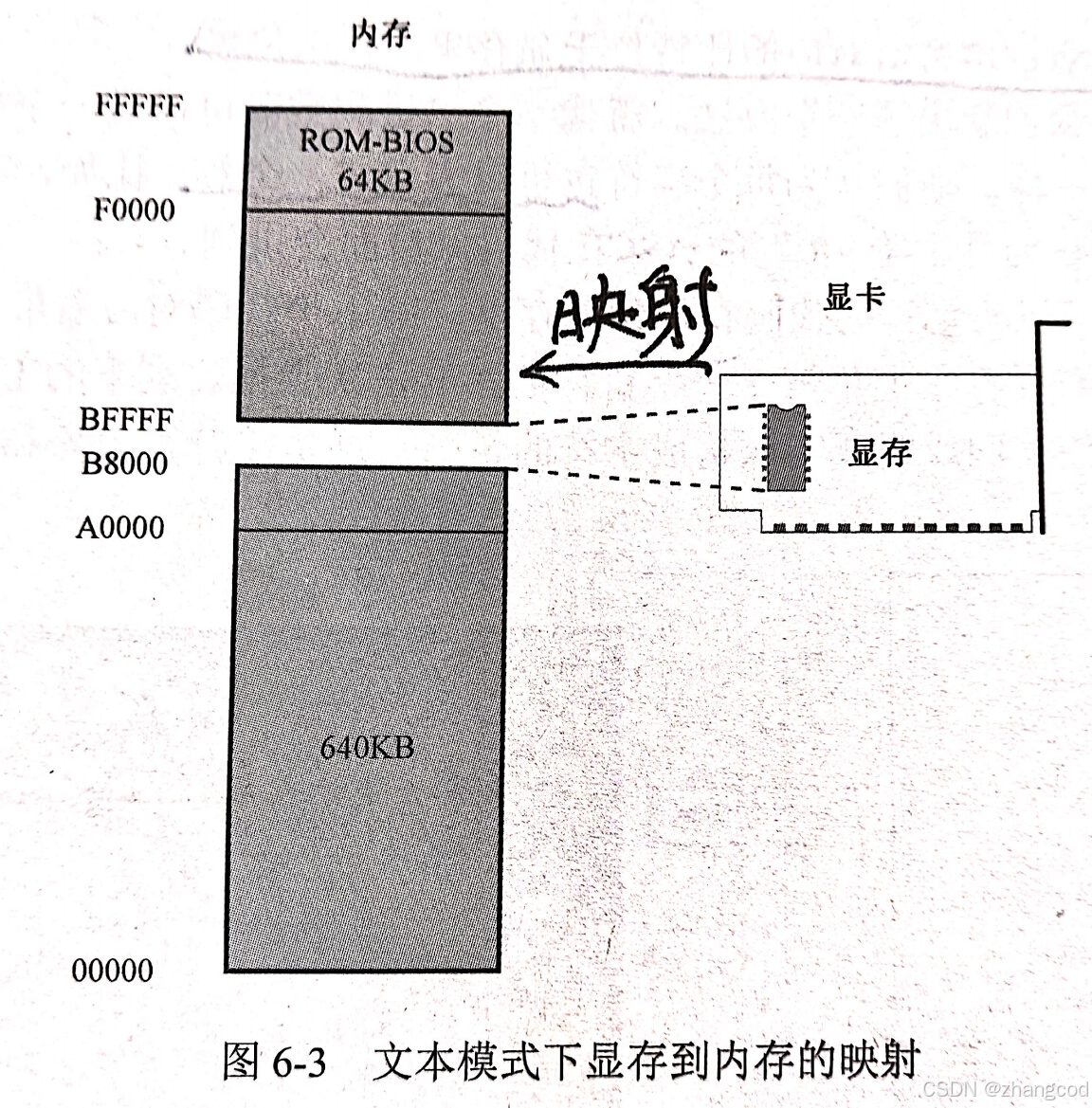
73.【C语言】C/C++的内存区域划分
目录 1.内存里的几个区域 2.示意图 3.解释 1.内存里的几个区域 除了耳熟能详的栈区,堆区,静态区,还有内核空间,内存映射段,数据段,代码段 2.示意图 3.解释 栈区(stack area):局部变量,函数参数,返回数据,返回地址 内存映射段:将文件映射到内存 映射的含义: 如果看过李忠…...
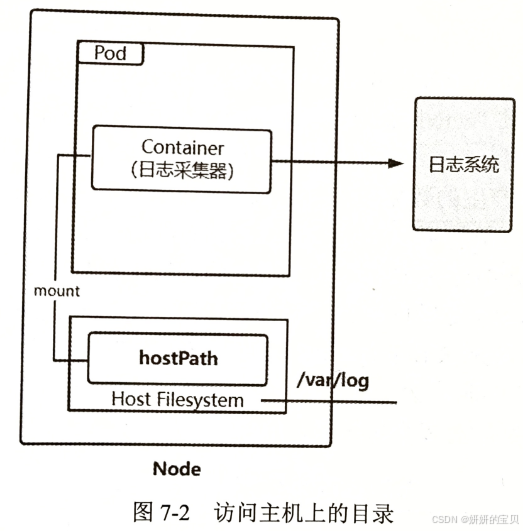
k8s 中存储之 hostPath 卷
目录 1 hostPath 卷介绍 2 hostPath 卷实际应用操作 2.1 创建 pod 资源类型 2.2 修改清单文件增加 hostPath 对应的参数配置 2.3 查看是否创建 卷 和 pod 2.4 创建发布文件测试是否正常访问 1 hostPath 卷介绍 EmptyDir中数据不会被持久化,它会随着Pod的结束而销…...
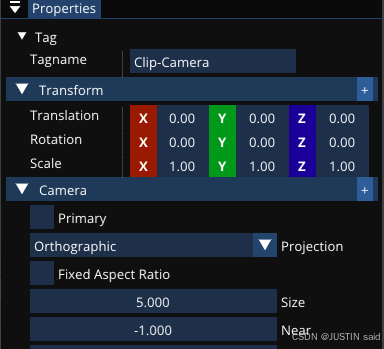
Cherno游戏引擎笔记(73~90)
------- scene viewport ---------- 》》》》做了两件事:设置视口和设置相机比例 》》》》为什么要设置 m_ViewportSize 为 glm::vec2 而不是 ImVec2 ? 因为后面需要进行 ! 运算,而 ImVec2 没有这个运算符的定义,只有 glm::vec2 有这个运算…...

helm 测试卸载或删除(redis)
作者:程序那点事儿 日期:2024/02/07 18:30 查看redis 集群实例 kubectl get all -n redis 卸载集群实例 helm uninstall redis -n redis 删除pvc kubectl get pvc -n redis kubectl delete pvc redis-data-redis-master-0 redis-data-redis-replicas…...

关于Qt音乐播放器进度条拖拽无用的问题解决方案
在使用Qt编写音乐播放器的时候,进度条关联播放音乐基本是必须的。那么在设计的过程中你可能会碰到一个奇怪的问题就是拖拽进度条的时候,可能会报错如下: 然后音乐就卡着不动了。。。 connect(ui->volume_toolButton,&VolumeToolBtn::…...

Redis:初识Redis
Redis:初识Redis Redis 介绍分布式架构Redis特性安装Redis Redis 介绍 在官网中,是如下介绍Redis的: in-memory data store used by millions of developers as a cache, vector database, document database, streaming engine, and messag…...

【React】增量传输与渲染
增量传输 增量传输是一种高效的文件传输方式,其核心原理在于只传输文件中发生变化的部分,而不是整个文件。以下是增量传输的详细解析: 定义与原理: 增量传输通过比对原始文件和目标文件,找出两者之间的差异部分&#…...
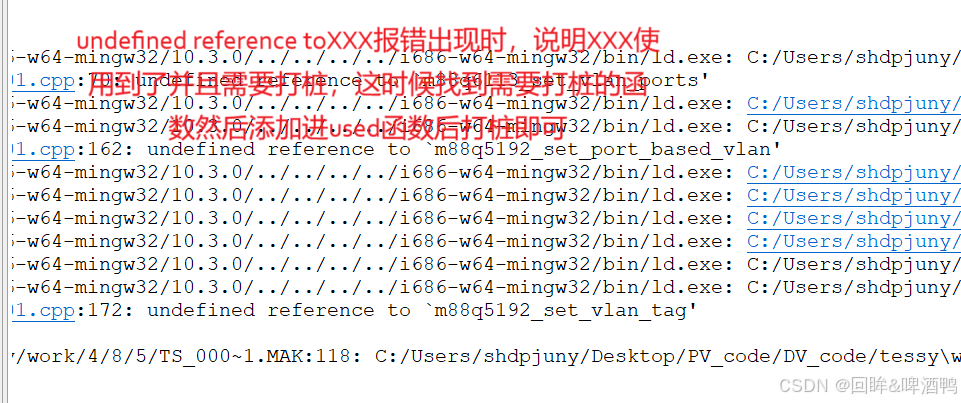
【回眸】Tessy 单元测试软件使用指南(四)常见报错及解决方案与批量初始化的经验
前言 分析时Tessy的报错 1.fatal error: Tricore/Compilers/Compilers.h: No such file or directory 2.error: #error "Compiler unsupported" 3.warning: invalid suffix on literal;C11 requires a space between literal and string macro 4.error: unknown…...

2024 - 10 :生物药学: 如何获取对应核心靶点基因的激酶
如何获取对应核心靶点基因的激酶 步骤 1:收集蛋白质信息 获取 UniProt ID: 对于每个基因,使用 UniProt 数据库获取其对应的蛋白质信息,包括 UniProt ID、序列和功能注释。UniProt 网站:https://www.uniprot.org/ 示…...
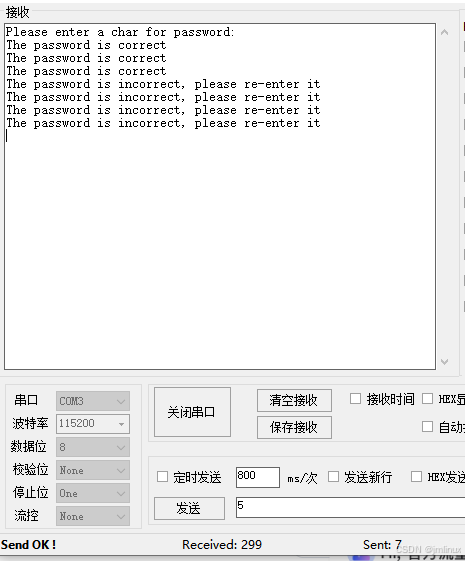
STM32 HAL库UART查询方式实例
本文中介绍USART编程涵盖了三种主要方法,详细介绍STM32F407微控制器结合HAL库,通过UART的查询方式来实现一个实用的密码验证程序。提示用户键入一个字符作为密码。只有当用户精准地输入字符6时,系统才会反馈“密码正确”的确认信息。反之&…...
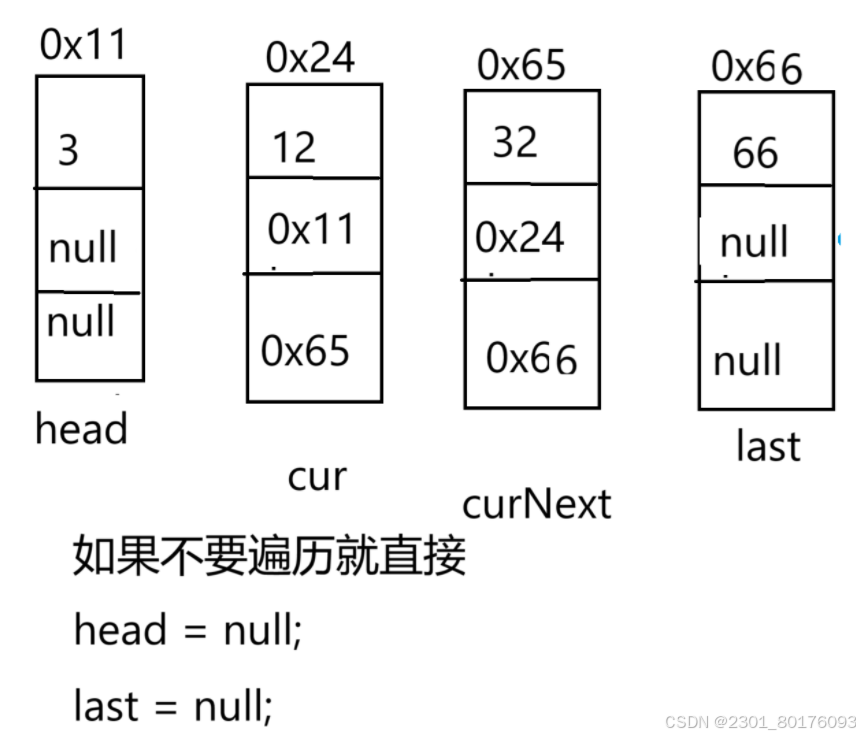
数据结构--线性表双向链表的实现
目录 思路设计 总体思维导图 插入部分 头插法尾插法 任意位置插入 删除部分 头结点 尾节点 中间节点 只有头结点且删除的就是头结点 编辑 清空链表部分 遍历清空链表的所有节点 不遍历清空 各部分代码 Main部分 MyListedList部分 IndexOutOfException部分 …...
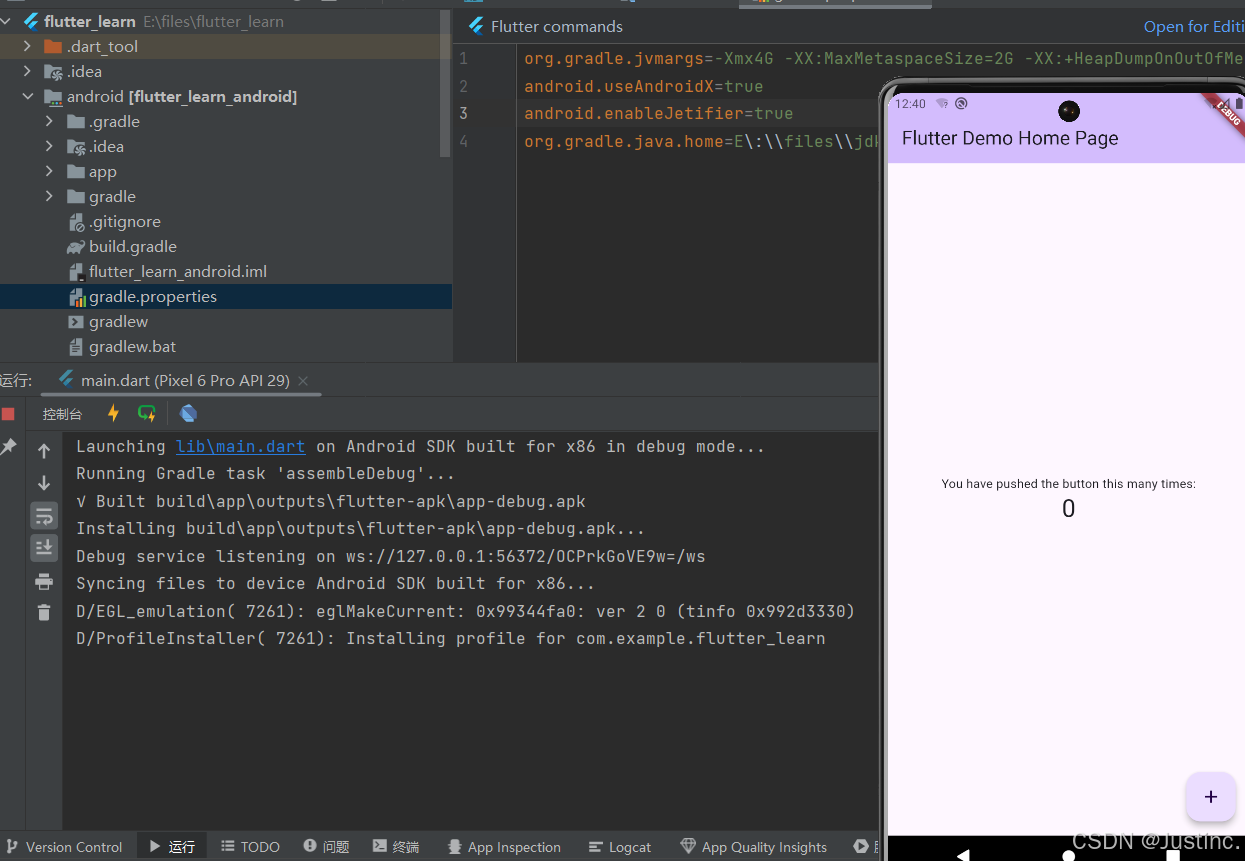
第一个Flutter应用(一)
1、创建项目 1.1 新建 1.2 选择Flutter SDK的位置 1.3 项目名称 英文单词加下划线起名规范,其他默认即可。 1.4 点击运行 发生报错显示我们的JAVA版本不符合 1.5 更改版本设置 1.6 再次启动项目 2、分析页面代码 以下是lib/main.dart的源代码(为了阅…...

批量查询快递单号物流信息:高效掌握最后更新动态
在电商和物流行业蓬勃发展的今天,快递单号的物流信息追踪显得尤为重要。对于商家和客户来说,了解包裹的最后更新物流状态是确保货物安全、及时送达的关键。本文将介绍如何批量查询快递单号的物流信息,帮助您高效掌握每个包裹的最新动态。 1运…...
随着硬件水平的提升,LabVIEW有哪些过去的编程方法被淘汰掉了
随着硬件水平的不断提升,尤其是处理器性能、存储能力、通信速度等方面的飞跃,LabVIEW的一些早期编程方法逐渐被更高效、现代的编程技术所取代。以下是一些随着硬件升级而逐步淘汰的LabVIEW编程方法和技术: 1. 低效的数据流传输方式 过去由于…...
Leetcode 206.反转链表
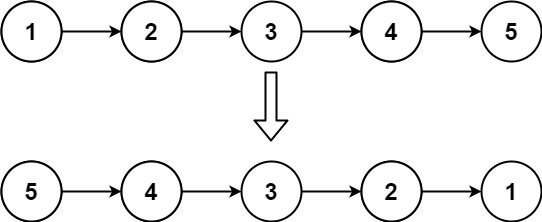
题目链接:206. 反转链表 - 力扣(LeetCode) 题目描述: 给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。 示例 1: 输入:head [1,2,3,4,5] 输出:[5,4,3,2,1] 解题思路…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

aardio 自动识别验证码输入
技术尝试 上周在发学习日志时有网友提议“在网页上识别验证码”,于是尝试整合图像识别与网页自动化技术,完成了这套模拟登录流程。核心思路是:截图验证码→OCR识别→自动填充表单→提交并验证结果。 代码在这里 import soImage; import we…...
C++中vector类型的介绍和使用
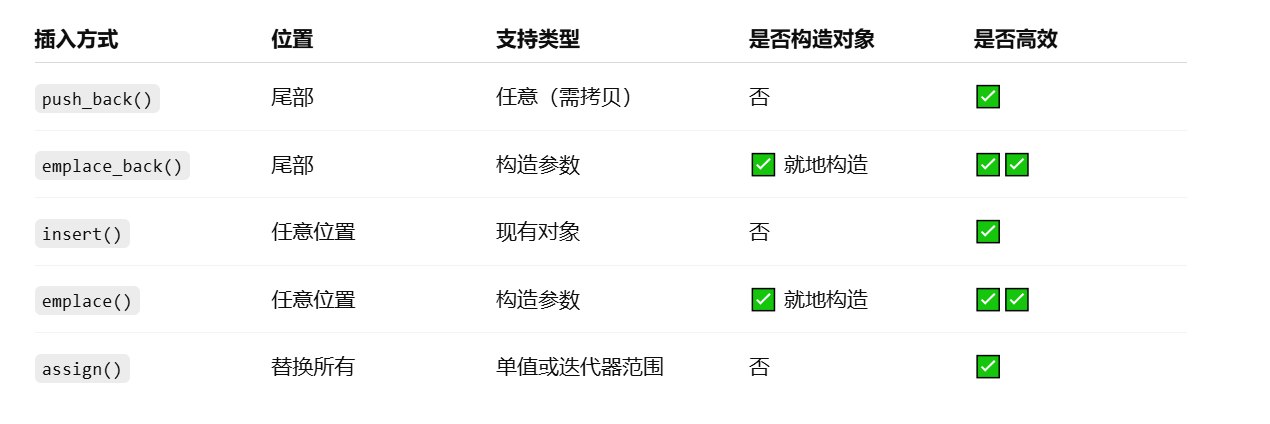
文章目录 一、vector 类型的简介1.1 基本介绍1.2 常见用法示例1.3 常见成员函数简表 二、vector 数据的插入2.1 push_back() —— 在尾部插入一个元素2.2 emplace_back() —— 在尾部“就地”构造对象2.3 insert() —— 在任意位置插入一个或多个元素2.4 emplace() —— 在任意…...

深入浅出JavaScript中的ArrayBuffer:二进制数据的“瑞士军刀”
深入浅出JavaScript中的ArrayBuffer:二进制数据的“瑞士军刀” 在JavaScript中,我们经常需要处理文本、数组、对象等数据类型。但当我们需要处理文件上传、图像处理、网络通信等场景时,单纯依赖字符串或数组就显得力不从心了。这时ÿ…...
