【无人机设计与控制】无人机三维路径规划,对比蚁群算法,ACO_Astar_RRT算法

摘要
本文探讨了三种不同的无人机三维路径规划算法,即蚁群算法(ACO)、A算法(Astar)以及快速随机树算法(RRT)。通过仿真实验对比了各算法在不同环境下的性能,包括路径长度、计算效率及其对动态障碍物的适应性。研究结果表明,蚁群算法在复杂环境中具有较强的全局优化能力,而A算法在简单场景下表现较优,RRT则适用于处理动态障碍物的情况。
理论
1. 蚁群算法(ACO)
蚁群算法是一种基于生物群体行为的启发式优化算法,模拟了蚂蚁在寻找食物过程中的路径选择。通过信息素的反馈机制,蚂蚁逐步优化路径。ACO在全局寻优方面表现良好,但易陷入局部最优。
2. A*算法(Astar)
A算法是一种广泛应用于路径规划的图搜索算法。它通过结合启发式估计(通常是欧几里得距离)与实际代价来选择最优路径。A算法以其计算简单、效率高的特点著称,但对于复杂环境或高维问题,其效率有所下降。
3. 快速随机树算法(RRT)
RRT是一种基于随机采样的路径规划算法,适合处理高维空间中的路径规划问题。该算法通过逐步扩展树结构来寻找路径,并在处理动态环境下具有较强的鲁棒性。然而,RRT生成的路径通常较长,后续需要进一步优化。
实验结果
通过MATLAB仿真实验,针对复杂环境中的无人机三维路径规划进行了对比。
-
实验环境
实验场景包括复杂的三维障碍物环境,使用无人机从起点飞行到指定目标点。每个算法均运行多次以获取平均性能数据。
-
对比结果
路径长度:ACO生成的路径相对较短,A* 次之,RRT生成的路径较长,但后续优化可以改善。 计算时间:A*算法的计算时间最短,ACO和RRT的计算时间相对较长。 动态障碍物适应性:RRT在处理动态障碍物时表现最佳,能够快速重新规划路径。
-
结果图示 以下图像展示了三种算法在相同实验场景中的路径规划结果。

部分代码
以下是蚁群算法与A*算法在三维空间中的路径规划MATLAB代码:
% ACO算法的简化实现% 参数初始化
numAnts = 20; % 蚂蚁数量
alpha = 1; % 信息素重要性因子
beta = 2; % 启发函数重要性因子
rho = 0.5; % 信息素挥发因子
iterations = 100; % 最大迭代次数% 地图初始化
mapSize = [100, 100, 100]; % 三维地图大小
startPoint = [1, 1, 1]; % 起点
endPoint = [100, 100, 100]; % 终点% 蚂蚁群路径选择
for i = 1:iterationsfor j = 1:numAnts% 生成每只蚂蚁的路径currentPath = generatePath(mapSize, startPoint, endPoint, alpha, beta);% 更新信息素updatePheromone(currentPath, rho);end
end
% A*算法的简化实现% 地图初始化
mapSize = [100, 100, 100]; % 三维地图大小
startPoint = [1, 1, 1]; % 起点
endPoint = [100, 100, 100]; % 终点% 启发式函数:欧几里得距离
heuristic = @(p1, p2) sqrt(sum((p1 - p2).^2));% A*路径规划主函数
openSet = [startPoint]; % 开放节点集
cameFrom = []; % 路径回溯while ~isempty(openSet)current = selectBestNode(openSet, heuristic);if isequal(current, endPoint)reconstructPath(cameFrom, current);break;endopenSet = removeNode(openSet, current);neighbors = getNeighbors(current, mapSize);for neighbor = neighbors% 更新邻居节点的代价tentative_gScore = calculateGScore(current, neighbor);if tentative_gScore < gScore(neighbor)cameFrom(neighbor) = current;openSet = addToOpenSet(openSet, neighbor);endend
end
参考文献
❝
Dorigo, M., & Stützle, T. (2004). Ant Colony Optimization. MIT Press.
Hart, P. E., Nilsson, N. J., & Raphael, B. (1968). A Formal Basis for the Heuristic Determination of Minimum Cost Paths. IEEE Transactions on Systems Science and Cybernetics, 4(2), 100-107.
LaValle, S. M. (1998). Rapidly-exploring random trees: A new tool for path planning. Technical Report, Computer Science Department, Iowa State University.
(文章内容仅供参考,具体效果以图片为准)
相关文章:

【无人机设计与控制】无人机三维路径规划,对比蚁群算法,ACO_Astar_RRT算法
摘要 本文探讨了三种不同的无人机三维路径规划算法,即蚁群算法(ACO)、A算法(Astar)以及快速随机树算法(RRT)。通过仿真实验对比了各算法在不同环境下的性能,包括路径长度、计算效率…...

毕设 大数据电影数据分析与可视化系统(源码+论文)
文章目录 0 前言1 项目运行效果2 设计概要3 最后 0 前言 🔥这两年开始毕业设计和毕业答辩的要求和难度不断提升,传统的毕设题目缺少创新和亮点,往往达不到毕业答辩的要求,这两年不断有学弟学妹告诉学长自己做的项目系统达不到老师…...

10月7日刷题记录
C C...

苍穹外卖学习笔记(十五)
文章目录 一. 缓存菜品缓存菜品DishController.java清除缓存数据 缓存套餐Spring Cachemaven坐标常用注解 入门案例springcachedemo.sqlpom.xmlapplication.ymlCacheDemoApplication.javaWebMvcConfiguration.javaUserController.javaUser.javaUserMapper.java 套餐管理SkyAppl…...

知识图谱入门——5:Neo4j Desktop安装和使用手册(小白向:Cypher 查询语言:逐步教程!Neo4j 优缺点分析)
Neo4j简介 Neo4j 是一个基于图结构的 NoSQL 数据库,专门用于存储、查询和管理图形数据。它的核心思想是使用节点、关系和属性来描述数据。图数据库非常适合那些需要处理复杂关系的数据集,如社交网络、推荐系统、知识图谱等领域。 与传统的关系型数据库…...

35个数据分析模型
这些数据分析模型覆盖了战略规划、市场营销、运营管理、用户行为、财务分析等多个方面,是企业和组织在进行决策分析时常用的工具。分享给大家,如果想要PDF下载: https://edu.cda.cn/group/4/thread/178782 1、SWOT模型 SWOT模型是一种战略分…...

Java | Leetcode Java题解之第457题环形数组是否存在循环
题目: 题解: class Solution {public boolean circularArrayLoop(int[] nums) {int n nums.length;for (int i 0; i < n; i) {if (nums[i] 0) {continue;}int slow i, fast next(nums, i);// 判断非零且方向相同while (nums[slow] * nums[fast]…...

date:10.4(Content:Mr.Peng)( C language practice)
void reverse(char* p, int len) {char* left p;char* right p len - 2;while (left < right){char* temp left;*left *right;//当*left*right后,*temp已经被改为f了*right *temp;//你再*temp赋值给*right时,已经没用了left;right--;}}int main…...

【K8S系列】Kubernetes 集群中的网络常见面试题
在 Kubernetes 面试中,网络是一个重要的主题。理解 Kubernetes 网络模型、服务发现、网络策略等概念对候选人来说至关重要。以下是一些常见的 Kubernetes 网络面试题及其答案,帮助你准备面试。 1. Kubernetes 的网络模型是什么样的? 问题&am…...
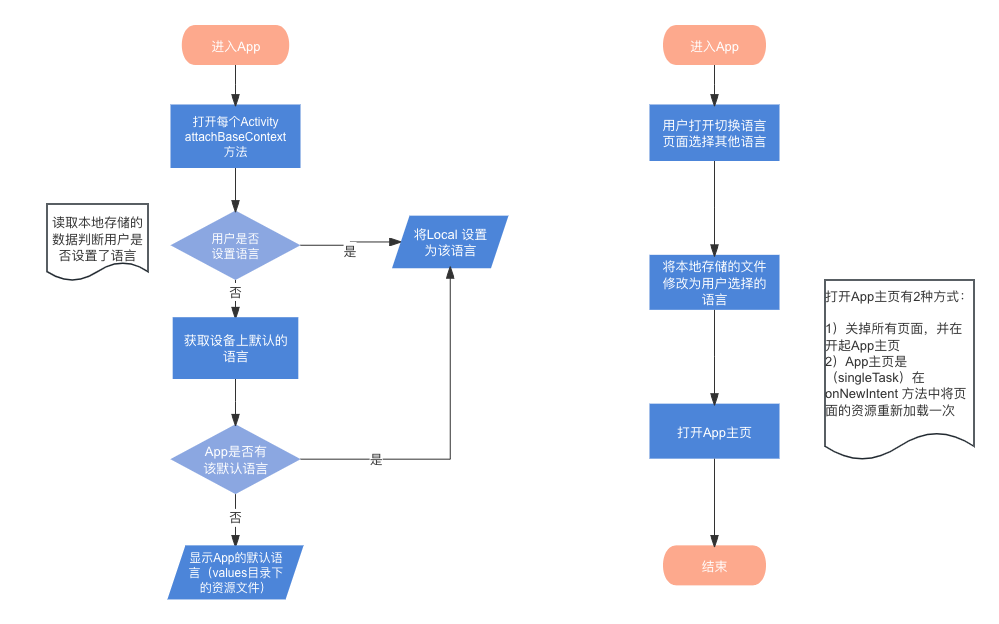
Android 无Bug版 多语言设计方案!
出海业务为什么要做多语言? 1.市场扩大与本地化需求: 通过支持多种语言,出海项目可以触及更广泛的国际用户群体,进而扩大其市场份额。 本地化是吸引国际用户的重要策略之一,而语言本地化是其中的核心。使用用户的母语…...
Nginx02-安装
零、文章目录 Nginx02-安装 1、Nginx官网 Nginx官网地址:http://nginx.org/ 2、Nginx下载 (1)Nginx下载 下载页地址:http://nginx.org/en/download.html (2)更老版本下载 下载页地址:http…...

大模型基础架构
Transformer 设计者:Google 特点:最流行,几乎所有大模型都用它 代码:https://github.com/openai/finetune-transformer-lm/blob/master/train.py RWKV 设计者:PENG Bo 特点:可并行训练,推理性…...
—— 聚合函数与分组查询)
MySQL 实验 10:数据查询(3)—— 聚合函数与分组查询
MySQL 实验 10:数据查询(3)—— 聚合函数与分组查询 目录 MySQL 实验 10:数据查询(3)—— 聚合函数与分组查询一、聚合函数1、计数函数(COUNT)2、求和函数(SUM࿰…...

感知机学习算法
感知机 一、感知机简介二、感知机模型2.1 感知机的基本组成2.2 求和函数2.2.1 时间总合2.2.2 空间总合 2.3 激活函数2.4 学习算法2.4.1 赫布学习规则2.4.2 Delta学习规则 三、 结论参考文献 一、感知机简介 M-P神经元模型因其对生物神经元激发过程的极大简化而成为神经网络研究…...
2024年双十一有什么好物推荐?双十一必买清单大汇总
随着科技的飞速发展,数码产品已成为我们生活中不可或缺的伙伴。2024年双十一购物狂欢节即将来临,众多消费者早已摩拳擦掌,准备在这个年度盛事中淘到心仪的数码好物。在这个信息爆炸的时代,如何从琳琅满目的商品中挑选出性价比高、…...

C语言贪吃蛇
#只讲逻辑不讲一些基础,基础大概过一遍就行# project-one: 无 (gitee.com)仓库里面有原代码 一、基础工作 1、先将你的编译器换成32位环境,也就是x86, 如果是控制台主机窗口则管,若不是需要改为控制台主机窗口 打开运行窗口后点…...

SpringBoot宠物咖啡馆平台:创新设计与高效实现
1系统概述 1.1 研究背景 随着计算机技术的发展以及计算机网络的逐渐普及,互联网成为人们查找信息的重要场所,二十一世纪是信息的时代,所以信息的管理显得特别重要。因此,使用计算机来管理基于Spring Boot的宠物咖啡馆平台的设计与…...

李宏毅深度学习-梯度下降和Batch Normalization批量归一化
Gradient Descent梯度下降 ▽ -> 梯度gradient -> vector向量 -> 下图中的红色箭头(loss等高线的法线方向) Tip1: Tuning your learning rates Adaptive Learning Rates自适应lr 通常lr会越来越小 Adaptive Learning Rates中每个参数都给它不…...

java集合框架都有哪些
Java集合框架(Java Collections Framework)是Java提供的一套设计良好的支持对一组对象进行操作的接口和类。这些接口和类定义了如何添加、删除、遍历和搜索集合中的元素。Java集合框架主要包括以下几个部分: 接口: Collection&…...
线程与进程)
笔记整理—linux进程部分(8)线程与进程
前面用了高级IO去实现鼠标和键盘的读取,也说过要用多进程方式进行该操作: int mian(void) {int ret-1;int fd-1;char bug[100]{0};retfork();if(0ret){//子进程,读鼠标}if(0<ret){//父进程,读键盘}else{perror("fork&quo…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...
