专题九_递归_算法专题详细总结
目录
递归
1.什么是递归?
2.为什么会用到递归?
3.如何理解递归?
1.递归展开的细节图
2.二叉树中的题目
3.宏观看待递归的过程
1) 不要在意细节的展开图
2) 把递归的函数当作一个黑盒
3) 相信这个黑盒一定能够完成这个任务
4.如何写好一个递归?
二、搜索 vs 深度优先遍历 vs 深度优先搜索 vs 宽度优先遍历 vs 宽度优先搜索 vs 暴搜
1.深度优先遍历 vs 深度优先搜索(dfs)编辑
2.宽度优先遍历 vs 宽度优先搜索(bfs)编辑
2.关系图
3.拓展搜索问题
三、回溯与剪枝
1.本质
1. 汉诺塔 (easy)
解析:
一步步拆解汉诺塔问题,了解为什么可以用递归来解决这道题目!!!
1.重复子问题 -> 函数头
2.只关心一个子问题在做什么 -> 函数体
3.递归的出口
总结:
2. 合并两个有序链表(easy)
解析:
1.考虑主问题 -> 寻找头函数
2.寻找子问题 -> 构造函数体
3.细节问题,返回出口
总结:
3. 反转链表(easy)
解析:
怎么用上递归?依旧是寻找子问题:第一种视角:从宏观的角度来解决问题
第二种视角:将链表看成一颗树
4. 两两交换链表中的节点(medium)
解析:
总结:
5. Pow(x, n)- 快速幂(medium)
解析:
1)暴力:就是2^10=2*2*2*2*2……,这种办法绝对会超时的
2)优化:快速幂
细节问题:
总结:
递归
1.什么是递归?
C语言+数据结构(二叉树、快排、归并)
函数自己调用自己的情况

2.为什么会用到递归?
本质:就是出现了相同的子问题
主问题 -> 相同的子问题
子问题 -> 相同的子问题
全都可以调用f()函数
3.如何理解递归?
1.递归展开的细节图
2.二叉树中的题目
3.宏观看待递归的过程
1) 不要在意细节的展开图
2) 把递归的函数当作一个黑盒
3) 相信这个黑盒一定能够完成这个任务
eg:二叉树的后序遍历
void dfs(TreeNode* root)
{//细节--出口if(root==nullptr) return;dfs(root->left); //不管三七21,我要先遍历我的左子树dfs(root->right); //然后在要遍历右子树,我相信这个递归函数一定能帮我完成printf(root->val); //最后再遍历自己
}eg:归并
void merge(nums,int left,int right)
{//细节问题-保证不能出现死递归if(left>=right) return;//1.先让左边排排序 2.右边排排序 3.然后合并两个数组 那么就要选取中间点int mid=(left+right)/2;merge(nums,left,mid);merge(nums,mid+1,right);//合并两个数组
}4.如何写好一个递归?
1.先找到相同的子问题!!! -> 函数头的设计
2.只关心某一个子问题是如何解决的 -> 函数体的书写
3.注意一下递归函数的出口即可
二、搜索 vs 深度优先遍历 vs 深度优先搜索 vs 宽度优先遍历 vs 宽度优先搜索 vs 暴搜
1.深度优先遍历 vs 深度优先搜索(dfs)

2.宽度优先遍历 vs 宽度优先搜索(bfs)

那么遍历只是形式,目的是搜索
2.关系图
暴力枚举一遍所有的情况
搜索(暴搜) dfs
3.拓展搜索问题
全排列
决策树

三、回溯与剪枝
1.本质
就是深搜dfs
回溯:就是尝试某一种情况,但是行不通的时候,退回到上一级的操作。
剪枝:当有多个分岔路口的时候,我们已经明白或者已经走过了某一条路,我们就不用再走这一条路,那么就把这条路直接剪掉,尝试别的路径。
递归:
1. 汉诺塔 (easy)

解析:
一步步拆解汉诺塔问题,了解为什么可以用递归来解决这道题目!!!

可以发现该汉诺塔问题存在许多重复的子问题。
那么就可以对于重复的子问题进行细分,来一步步书写代码。
1.重复子问题 -> 函数头
将A(x)柱子上的一堆盘子,借助B(y)柱子,转移到C(z)柱子上

void dfs(x,y,z,int n);
2.只关心一个子问题在做什么 -> 函数体
第一步:

这n-1个盘子要通过z的帮助,来转移到y上,那么函数体就是:
dfs(x,z,y,int n-1);
第二步:

将A(x)上的最后一块盘子转移到C(z)上:
x.back() -> z
第三步:
就是将这n-1块盘子通过A(x)转移到C(z)上:
dfs(y,x,z,int n-1);
3.递归的出口
当N==1 的时候,就只用放到C盘上就可以了。
class Solution {
public:void hanota(vector<int>& A, vector<int>& B, vector<int>& C) {dfs(A,B,C,A.size());}void dfs(vector<int>& x,vector<int>& y,vector<int>& z,int N){if(N==1){z.push_back(x.back());x.pop_back();return;}dfs(x,z,y,N-1);z.push_back(x.back());x.pop_back();dfs(y,x,z,N-1);}
};总结:
这里唯一需要注意的就是当x上的盘子移动到z上时,唯一的不同就是要将x.back()也就是最后一个元素移动到z上,并不是首元素进行移动。
2. 合并两个有序链表(easy)

解析:
依旧是考虑这题为什么能够用到递归,那么就是来寻找子问题:
1.考虑主问题 -> 寻找头函数
主问题就是合并两个有序链表,那么最后返回的就是开始头节点较小的那个指针
2.寻找子问题 -> 构造函数体

假设l1这个指针是一个较小的指针,那么就让它来连接l1->next 后面的链表跟 l2后面的链表进行结合的有序链表,那么子问题的函数体就也是合并两个有序链表。
这个函数体就总结成谁小,谁做表头,去连接剩下两个有序链表合并后的结果。
if(l1->val<l2->val) {l1->next=mergeTwoLists(l1->next,l2);return l1;}else {l2->next=mergeTwoLists(l1,l2->next);return l2;}最后不要忘记的就是连接完后,要返回该位置的头节点,来给上一层的链表进行连接。
3.细节问题,返回出口
当某一个链表为空的时候,就返回另一个链表
if(l1==nullptr) return l2;
if(l2==nullptr) return l1;
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {if(l1==nullptr) return l2;if(l2==nullptr) return l1;if(l1->val<l2->val) {l1->next=mergeTwoLists(l1->next,l2);return l1;}else {l2->next=mergeTwoLists(l1,l2->next);return l2;}}
};总结:
循环(迭代)vs 递归
这些都是解决重复子问题
证明他们都是可以互相转换的,那么什么时候循环舒服?什么时候递归舒服?

当这个决策树很恶心的时候,肯定就是用递归更爽,举个例子,假如只是递归一个数组,它的决策树就是只有一个左子树,很简单,那么这个递归改循环就很简单。

//对于循环
for(int i=0;i<n;i++)
{cout<<nums[i]<<" ";
}
cout<<endl;//对于递归
dfs(nums,0);void dfs(vector<int>& nums,int i)
{//递归出口if(i==nums.size()) return;cout<<nums[i]<<" ";dfs(nums,i+1);
}3. 反转链表(easy)
简单的翻转链表,在上一个专题就已经通过指针迭代的方式完成过。

解析:
怎么用上递归?依旧是寻找子问题:
第一种视角:从宏观的角度来解决问题

1.让当前节点后面的链表先逆置,并且把头节点返回;
2.让当前节点添加到逆置后的链表后面即可。
第二种视角:将链表看成一颗树
仅需做一次dfs即可,进行后序遍历。

/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* reverseList(ListNode* head) {if(head==nullptr||head->next==nullptr) return head;ListNode* newHead=reverseList(head->next);//接受head->next 后面链表逆置的结果head->next->next=head;head->next=nullptr;return newHead;}
};总结:
从宏观的角度上看,依旧是对递归特别好的理解,假如我从第一个头节点开始,我来进行翻转的时候,把head->next 后面的所有链表都交给我的主函数reverseList(head->next); 因为我所有的子问题都是相同的,都是要进行对链表的翻转,那么每次翻转完成,我都将翻转后的头节点存入newhead里面,那么最后翻转完成后一定返回的是newhead。
待物将第一个节点后面所有链表节点交给这个函数后,证明他已经被反转,那么我只需要注意当前我的head->next->next=head,就是让后面的被翻转完成的链表指向我自己;
head=nullptr,就保证在每一层递归内的操作都是一样的,保证最后一个节点就指向的是nullptr

4. 两两交换链表中的节点(medium)

解析:
两两交换链表的节点,这题用递归简直跟上一题一模一样。
在宏观上:
先交换前两个节点的后面所有的链表节点

只用判断离我们最近且最开始的两个带交换的节点进行具体的详细操作就OK,然后递归函数就传入head->next->next;的值
1.函数头
ListNode* tmp=swapPairs(head->next->next);
2.函数体
ListNode* tmp=swapPairs(head->next->next);ListNode* ret=head->next;head->next->next=head;head->next=tmp;3.函数出口
if(head==nullptr||head->next==nullptr) return head;
最后因为返回头节点是ret,所以要单独记录一下。
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* swapPairs(ListNode* head) {if(head==nullptr||head->next==nullptr) return head;ListNode* tmp=swapPairs(head->next->next);ListNode* ret=head->next;head->next->next=head;head->next=tmp;return ret;}
};总结:
写这种递归问题就要在宏观的角度上去观察它,然后把除了第一次详细处理的操作单独拿出来后,其他后面的所有操作都留给递归函数去完成。
5. Pow(x, n)- 快速幂(medium)

解析:
1)暴力:
就是2^10=2*2*2*2*2……,这种办法绝对会超时的
2)优化:快速幂
实现快速幂:1.递归 2.循环

考虑了快速幂的算法问题,那么只要考虑三步即可:
1.相同子问题 -> 函数头
int pow(x,n);
2.只关心每一个子问题做了什么 -> 函数体
tmp = pow(x,n/2);
return n%2==0 ? tmp * tmp : tmp * tmp * x;
3.递归出口
if(n==0) return 1;
细节问题:
1.n可能是负数
那么 3^(-2) = 1/(3^2)
2.n可能是-2^31 这样int存不下,要用long long
class Solution {
public:double myPow(double x, int n) {return n<0?1/dfs(x,n):dfs(x,n);}double dfs(double x,int n){if(n==0) return 1;double tmp=dfs(x,n/2);return n%2==0?tmp*tmp:tmp*tmp*x;}
};总结:
这里最主要的就是快速幂的算法原理,要注意考虑每一阶段中dfs传入的都是n/2,然后考虑n%2是否==0,再就是考虑到n<0时求pow幂的倒数。注意double范围。
总结一下吧~这节对我的帮助真的很大,希望对你也是!!!
相关文章:

专题九_递归_算法专题详细总结
目录 递归 1.什么是递归? 2.为什么会用到递归? 3.如何理解递归? 1.递归展开的细节图 2.二叉树中的题目 3.宏观看待递归的过程 1) 不要在意细节的展开图 2) 把递归的函数当作一个黑盒 3) 相信这个黑盒一定能够完成这个任务 4.如何写…...
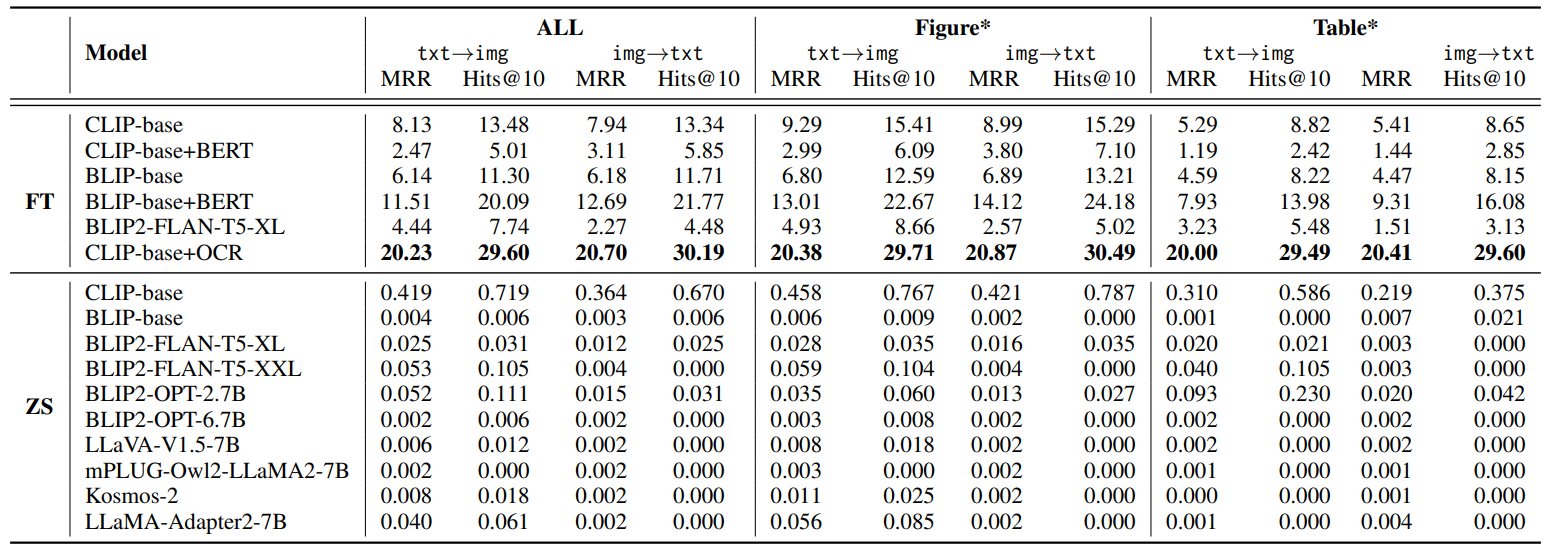
性能赶超GPT-4!多模态检索最新成果刷爆SOTA!顶会思路确定不学?
关注各大顶会的同学们都知道,今年多模态相关的主题可谓是火爆非常,有许多突破性成果被提出,比如最新的多模态检索增强框架MORE,生成性能猛超GPT-4! 再比如多模态检索模型MARVEL,在所有基准上实现SOTA&…...

基于 Qwen2.5-0.5B 微调训练 Ner 命名实体识别任务
一、Qwen2.5 & 数据集 Qwen2.5 是 Qwen 大型语言模型的最新系列,参数范围从 0.5B 到 72B 不等。 对比 Qwen2 最新的 Qwen2.5 进行了以下改进: 知识明显增加,并且大大提高了编码和数学能力。在指令跟随、生成长文本(超过 8K…...

16【Protues51单片机仿真】智能洗衣机倒计时系统
目录 一、主要功能 二、硬件资源 三、程序编程 四、实现现象 一、主要功能 用直流电机转动模拟洗衣机。要求 有弱洗、普通洗、强洗三种模式,可通过按键选择。可以设置洗衣时长,通关按键选择15、30、45、60、90分钟。时间到蜂鸣器报警提示。LCD 显示…...
爱心曲线公式大全
local r a*((math.sin(angle) * math.sqrt(math.abs(math.cos(angle)))) / (math.sin(angle) 1.4142) - 2 * math.sin(angle) 2) local x r * math.cos(angle) -- 计算对应的x值 local z r * math.sin(angle) 1.5*a - --曲线公式绘画 local function generateParabola()…...

新书速览|你好,C++
《你好,C》 本书内容 《你好,C》主要介绍C开发环境的搭建、基础语法知识、面向对象编程思想以及标准模板库的应用,特别针对初学者在学习C过程中可能遇到的难点提供了解决方案。全书共分13章,以一个工资程序的不断优化和完善为线索…...

ufw:Linux网络防火墙
一、命令简介 ufw(Uncomplicated Firewall)是一个为 Linux 系统提供简单易用的命令行界面的防火墙管理工具。它是基于 iptables 的,但提供了更简洁的语法和更直观的操作方式,使得配置防火墙变得更加简单,特别适…...

[C++]使用纯opencv部署yolov11-cls图像分类onnx模型
【算法介绍】 在C中使用纯OpenCV部署YOLOv11-cls图像分类ONNX模型是一项具有挑战性的任务,因为YOLOv11通常是用PyTorch等深度学习框架实现的,而OpenCV本身并不直接支持加载和运行PyTorch模型。然而,可以通过一些间接的方法来实现这一目标&am…...

如何使用Immersity AI将图片转换成3D效果视频
随着技术的进步,图片处理变得越来越强大和直观。借助Immersity AI这样的工具,我们现在可以轻松地将平面图片转换成3D效果视频。以下是如何使用Immersity AI进行这一转换的详细步骤。 第一步:访问Immersity AI网站 首先,打开你的…...

安全运营 -- GPO审计
0x00 背景 审计GPO,目的是审计哪些GPO权限分配不合理,包括但不限于审计预期以外的用户具有对GPO的写权限。 0x01 开启审核 在一台windows服务器上 开始 -- 运行 -- 输入 server manager 依次点击Manage -- Add Roles and Features Wizard 角色和功能…...
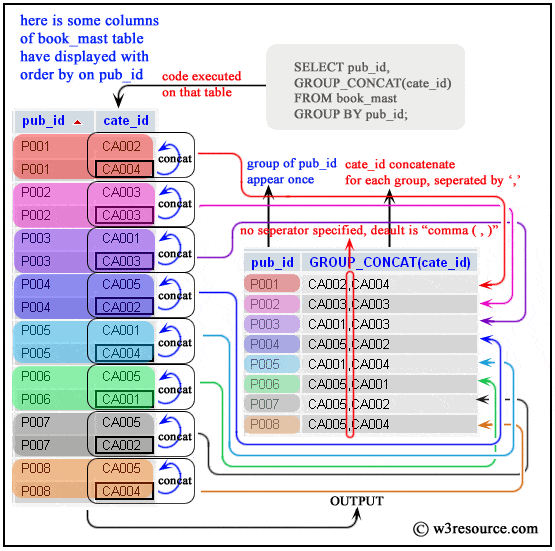
thinkphp6入门(25)-- 分组查询 GROUP_CONCAT
假设表名为 user_courses,字段为 user_id 和 course_name,存储每个用户选修的课程,想查询每个学生选修的所有课程 SQL 原生查询 SELECT user_id, GROUP_CONCAT(course_name) as courses FROM user_courses GROUP BY user_id; ThinkPHP 代码…...

小米 MIX FOLD工程固件 更换字库修复分区 资源预览与刷写说明
小米 MIX FOLD机型代号 :cetus 该手机搭载骁龙888旗舰处理器 。对于一些因为字库问题损坏导致的故障,更换字库后要先刷写对应的工程底层修复固件。绑定cpu后在写入miui量产固件。 通过博文了解 1💝💝💝-----此机型工程固件的资源刷写注意事项 2💝💝💝-----此…...

Flutter全局统一自定义导航栏返回按钮
Flutter全局统一自定义导航栏返回按钮 在Flutter开发中,导航栏(AppBar)是用户界面的重要组成部分,它不仅提供了页面标题,还可能包含返回按钮、导航按钮等。默认情况下,每个Scaffold的AppBar都会包含一个返…...
微信图片的超能力:5大隐秘功能揭秘,让你成为信息处理大师
在数字化时代,微信已成为我们日常生活中不可或缺的通讯工具。 它不仅仅是聊天的平台,更是一个功能强大的信息处理工具。 今天,我们将揭秘微信中图片背后的五大隐秘功能,让你在使用微信时更加得心应手,成为信息处理的…...

python实现RC4加解密算法
RC4算法 一、算法介绍1.1 背景1.2 密钥调度算法(KSA)1.3 伪随机生成算法(PRGA) 二、代码实现三、演示效果 一、算法介绍 1.1 背景 RC4算法是由Ron Rivest在1987年为RSA数据安全公司设计的一种流密码算法,其安全性主要依赖于其密钥流的随机性和不可预测性。该算法因…...

BLE MESH学习2——自定义MESH网络架构思考
BLE MESH学习2——自定义MESH网络架构思考 基于对WCH CH582这款单片机的了解,其可以实现mesh配网、朋友节点、低功耗节点和中继节点的角色,基本功能无问题。在此基础上,考虑满足IoT需求的MESH架构设计,作为后续设计的“白皮书”。…...

路由器的工作机制
在一个家庭或者一个公司中 路由器的作用主要有两个(①路由–决定了数据包从来源到目的地的路径 通过映射表决定 ②转送–通过路由器知道了映射表 就可以将数据包从路由器的输入端转移给合适的输出端) 我们可以画一张图来分析一下: 我们好好来解析一下这张图&#x…...

Studying-多线程学习Part3 - condition_variable与其使用场景、C++11实现跨平台线程池
来源:多线程学习 目录 condition_variable与其使用场景 生产者与消费者模型 C11实现跨平台线程池 condition_variable与其使用场景 生产者与消费者模型 生产者-消费者模式是一种经典的多线程设计模式,用于解决多个线程之间的数据共享和协作问题。…...
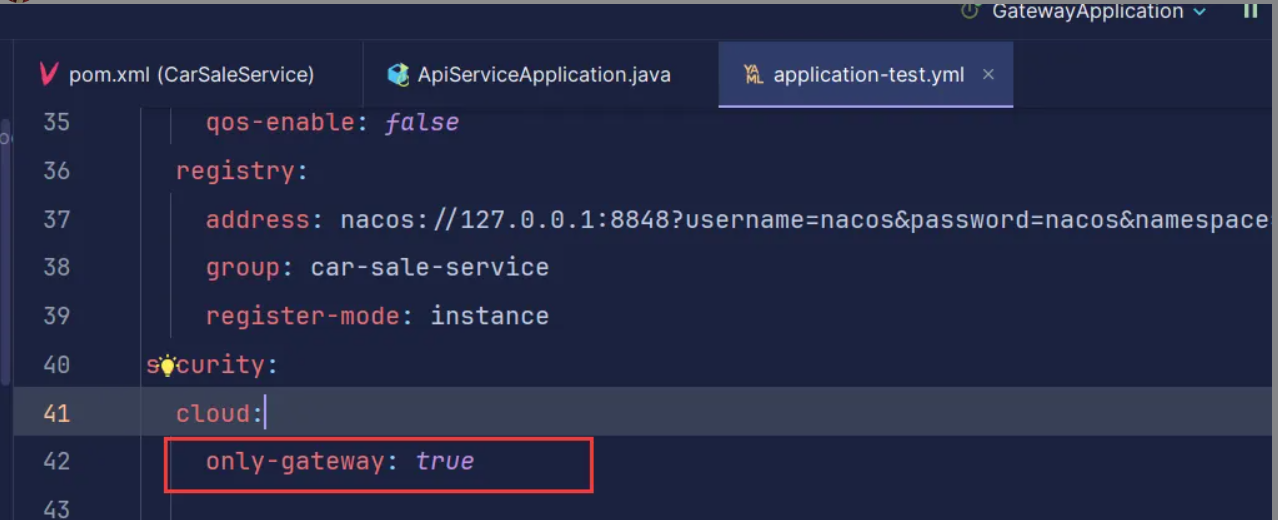
开发自定义starter
环境:Spring Cloud Gateway 需求:防止用户绕过网关直接访问服务器,用户只需引入依赖即可。 1、创建项目 首先创建一个spring boot项目 2、配置pom.xml <?xml version"1.0" encoding"UTF-8"?> <project xm…...

Vue2电商平台(五)、加入购物车,购物车页面
文章目录 一、加入购物车1. 添加到购物车的接口2. 点击按钮的回调函数3. 请求成功后进行路由跳转(1)、创建路由并配置路由规则(2)、路由跳转并传参(本地存储) 二、购物车页面的业务1. uuid生成用户id2. 获取购物车数据3. 计算打勾商品总价4. 全选与商品打勾(1)、商品全部打勾&a…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...
