算法讲解—最小生成树（Kruskal 算法）

算法讲解—最小生成树（Kruskal 算法）

简介

根据度娘的解释我们可以知道，最小生成树(Minimum Spanning Tree, MST)就是：一个有 $n$ 个结点的连通图的生成树是原图的极小连通子图，且包含原图中的所有 $n$ 个结点，并且有保持图连通的最少的边。

简单点来说就是求最小的连通图，就是从一个点能到达图的任意一点，且花费的代价最小（所有边的权值最小）。

最小生成树问题通常用于网络设计、电路设计等领域，目的是找到连接所有节点的最低成本方式。常见的算法有克鲁斯卡尔算法（Kruskal）和普里姆算法（Prim）等。

Kruskal 算法

要实现最小生成树，最著名的就是 Kruskal 算法。

Kruskal 算法是一种用来求解最小生成树问题的贪心算法。最小生成树问题是指在一个连通带权无向图中找到一个生成树，使得所有边的权重之和最小。

Kruskal 算法的基本思想是从小到大选择边，直到选出 $n-1$ 条边为止（$n$ 为节点数）。具体步骤如下：

1. 将图中的所有边按照权重从小到大进行排序。

2. 初始化一个空的集合 $M$，用来存放最小生成树的边。

3. 遍历排序后的边，如果当前边的两个端点不在同一个连通分量中，则将这条边加入集合 $M$ ，并将两个端点所在的连通分量合并。

4. 重复步骤 $3$，直到集合 $M$ 中的边数达到 $n-1$ 条，其中 $n$ 为节点数。

5. 最后得到的集合 $M$ 就是最小生成树。

Kruskal 算法的时间复杂度主要取决于排序边的时间复杂度，通常使用快速排序等快速的排序算法，因此总的时间复杂度为 $O(E\log E)$，其中 $E$ 为边数。

需要注意的是，在实际应用中，Kruskal 算法还需要对图进行一些预处理，如可以先对边进行去重、排序等操作，以提高算法的效率。

引用一张百度的图片

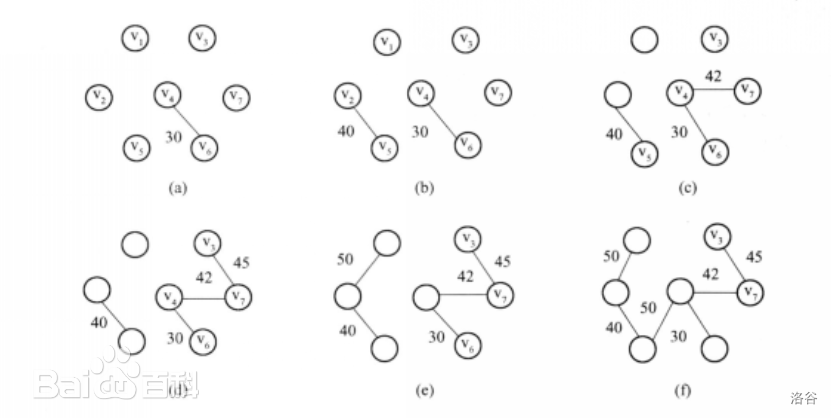
代码实现

Python(由 AI 生成）

class DisjointSet:def __init__(self):self.parent = {}self.rank = {}def make_set(self, node):self.parent[node] = nodeself.rank[node] = 0def find_set(self, node):if self.parent[node] != node:self.parent[node] = self.find_set(self.parent[node])return self.parent[node]def union_sets(self, node1, node2):root1 = self.find_set(node1)root2 = self.find_set(node2)if root1 != root2:if self.rank[root1] > self.rank[root2]:self.parent[root2] = root1elif self.rank[root1] < self.rank[root2]:self.parent[root1] = root2else:self.parent[root2] = root1self.rank[root1] += 1def kruskal(edges, n):disjoint_set = DisjointSet()for i in range(n):disjoint_set.make_set(i)edges.sort(key=lambda edge: edge[2])result = []for edge in edges:node1, node2, weight = edgeroot1 = disjoint_set.find_set(node1)root2 = disjoint_set.find_set(node2)if root1 != root2:disjoint_set.union_sets(node1, node2)result.append(edge)return result

C++ (由 AI 生成）

#include <iostream>
#include <vector>
#include <algorithm>using namespace std;struct Edge {int u, v, weight;bool operator<(const Edge& other) const {return weight < other.weight;}
};int findParent(vector<int>& parent, int i) {if (parent[i] == -1) return i;return parent[i] = findParent(parent, parent[i]);
}void kruskal(vector<Edge>& edges, int n) {vector<int> parent(n, -1);int num_edges = 0;int result = 0;sort(edges.begin(), edges.end());for (const auto& edge : edges) {int u_parent = findParent(parent, edge.u);int v_parent = findParent(parent, edge.v);if (u_parent != v_parent) {parent[u_parent] = v_parent;result += edge.weight;num_edges++;if (num_edges == n - 1) break;  // 加上n-1条边即可构成最小生成树}}if (num_edges < n - 1) {cout << "无法构成最小生成树" << endl;} else {cout << "最小生成树的权值总和为: " << result << endl;}
}int main() {int n, m; // n为顶点数，m为边数cin >> n >> m;vector<Edge> edges(m);for (int i = 0; i < m; ++i) {int u, v, weight;cin >> u >> v >> weight;edges[i] = {u, v, weight};}kruskal(edges, n);return 0;
}

洛谷模版题

【洛谷】P3366 【模板】最小生成树

板子代码

#include <bits/stdc++.h>
using namespace std;
int n, m, sum, ans, fa[10005];
struct node {int x, y, z;
}f[200005];
int find(int x) {return x == fa[x] ? x : fa[x] = find(fa[x]);}
bool cmp (node a, node b) {return a.z < b.z;}
int main() {cin >> n >> m;for (int i = 1; i <= n; i ++) {fa[i] = i;}for (int i = 1; i <= m; i ++) {cin >> f[i].x >> f[i].y >> f[i].z;}sort (f + 1, f + m + 1, cmp);	for (int i = 1; i <= m; i ++) {if (find(f[i].x) != find(f[i].y)) {sum ++;fa[find(f[i].y)] = find(f[i].x);ans += f[i].z;	} else continue;if (sum == n - 1) {cout << ans;return 0;}}cout << "orz";return 0;
}

推荐好题

【洛谷】 P1194 买礼物
详细讲解

【洛谷】P1396 营救
详细讲解

【洛谷】P2820 局域网
详细讲解

【洛谷】P2330 SCOI2005 繁忙的都市
详细讲解

【洛谷】P3623 APIO2008 免费道路
详细讲解

参考

• https://baike.baidu.com/item/%E6%9C%80%E5%B0%8F%E7%94%9F%E6%88%90%E6%A0%91/5223845?fr=ge_ala

• https://blog.csdn.net/2301_79188764/article/details/142172901

• https://www.dotcpp.com/course/1061

• https://baike.baidu.com/item/%E5%85%8B%E9%B2%81%E6%96%AF%E5%8D%A1%E5%B0%94%E7%AE%97%E6%B3%95/4455899?fr=ge_ala