DAY27||回溯算法基础 | 77.组合| 216.组合总和Ⅲ | 17.电话号码的字母组合

回溯算法基础知识

一种效率不高的暴力搜索法。本质是穷举。有些问题能穷举出来就不错了。

回溯算法解决的问题有：

• 组合问题：N个数里面按一定规则找出k个数的集合
• 切割问题：一个字符串按一定规则有几种切割方式
• 子集问题：一个N个数的集合里有多少符合条件的子集
• 排列问题：N个数按一定规则全排列，有几种排列方式
• 棋盘问题：N皇后，解数独等等

如何理解

回溯法解决的问题都可以抽象为树形结构，是的，我指的是所有回溯法的问题都可以抽象为树形结构！

因为回溯法解决的都是在集合中递归查找子集，集合的大小就构成了树的宽度，递归的深度就构成了树的深度。

递归就要有终止条件，所以必然是一棵高度有限的树（N叉树）。

• 回溯搜索的遍历过程

在上面我们提到了，回溯法一般是在集合中递归搜索，集合的大小构成了树的宽度，递归的深度构成的树的深度。

如图：

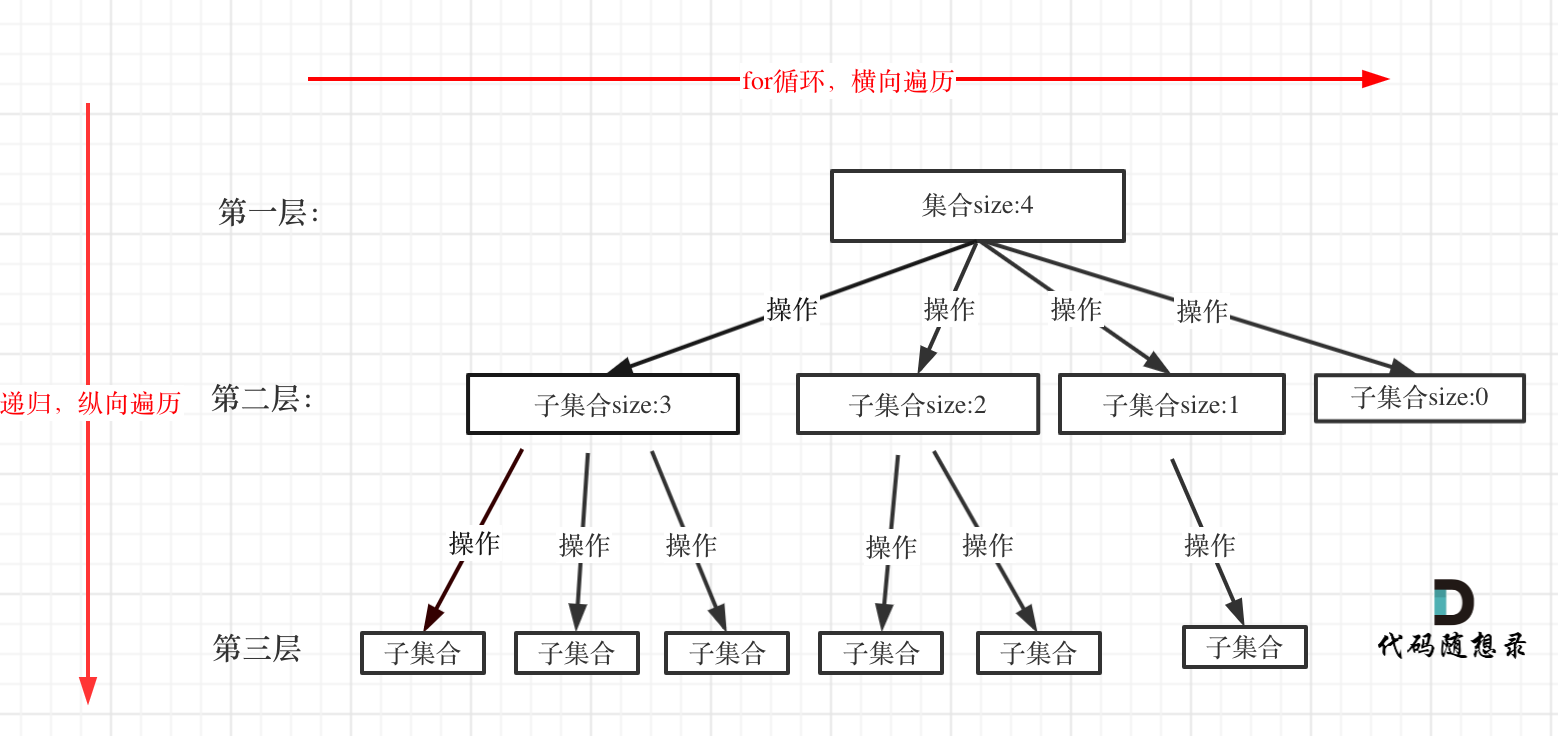
回溯算法模板

void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {处理节点;backtracking(路径，选择列表); // 递归回溯，撤销处理结果}
}

77.组合 

题目：77. 组合 - 力扣（LeetCode）

给定两个整数 n 和 k，返回 1 ... n 中所有可能的 k 个数的组合。

示例: 输入: n = 4, k = 2 输出: [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4], ]

递归里有for循环。

抽象成树形结构 

然后就是经典的回溯三部曲

·递归函数的参数和返回值

·回溯终止条件

·单层递归逻辑（单层搜索过程）

代码

class Solution {vector<vector<int>>result;vector<int>path;private:void backtraking(int n,int k,int startIndex){if(path.size()==k)//终止条件{result.push_back(path);//记录路径结果return;}//单层搜索过程for(int i=startIndex;i<=n;i++){path.push_back(i);backtraking(n,k,i+1);//递归搜索path.pop_back();//回溯，撤销操作}}
public:vector<vector<int>> combine(int n, int k) {backtraking(n,k,1);return result;}
};

这个和找二叉树路径总和那题还挺像的。

剪枝优化写法

来举一个例子，n = 4，k = 4的话，那么第一层for循环的时候，从元素2开始的遍历都没有意义了。 在第二层for循环，从元素3开始的遍历都没有意义了。

这么说有点抽象，如图所示：

图中每一个节点（图中为矩形），就代表本层的一个for循环，那么每一层的for循环从第二个数开始遍历的话，都没有意义，都是无效遍历。

所以，可以剪枝的地方就在递归中每一层的for循环所选择的起始位置。

如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了，那么就没有必要搜索了。

优化过程：

1. 已经选择的元素个数：path.size();

2. 还需要的元素个数为: k - path.size();

3. 在集合n中至多要从该起始位置 : n - (k - path.size()) + 1，开始遍历

为什么有个+1呢，因为包括起始位置，我们要是一个左闭的集合。

举个例子，n = 4，k = 3， 目前已经选取的元素为0（path.size为0），n - (k - 0) + 1 即 4 - ( 3 - 0) + 1 = 2。

从2开始搜索都是合理的，可以是组合[2, 3, 4]。

所以优化之后的for循环是：

for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) // i为本次搜索的起始位置

 216.组合总和Ⅲ

题目：216. 组合总和 III - 力扣（LeetCode）

找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数，并且每种组合中不存在重复的数字。

说明：

• 所有数字都是正整数。
• 解集不能包含重复的组合。

示例 1: 输入: k = 3, n = 7 输出: [[1,2,4]]

示例 2: 输入: k = 3, n = 9 输出: [[1,2,6], [1,3,5], [2,3,4]]

图思路

未剪枝版本

class Solution {private:vector<vector<int>>result;vector<int>path;void backtraking(int k,int n,int sum,int startindex){if(path.size()==k){if(sum==n)result.push_back(path);return;//如果path.size() == k 但sum != targetSum 直接返回}for(int i=startindex;i<=9;i++){sum+=i;path.push_back(i);backtraking(k,n,sum,i+1);//回溯操作，发生于当第一个if条件满足后，不管sum是否得到结果，然后继续遍历所有情况sum-=i;path.pop_back();}//这里注意我自己写的差别就是，不需要if判断sum是否大等小于目标值的情况。}
public:vector<vector<int>> combinationSum3(int k, int n) {result.clear();path.clear();backtraking(k,n,0,1);return result;}
};

在回溯算法中，回溯操作的发生时机通常是在满足某种条件后或者在尝试所有可能性后。具体来说，在组合求和问题中，回溯操作的发生时机有两个主要情况：

条件达成时的回溯：

当当前路径 path 的长度达到了要求的 k（即 path.size() == k），并且当前路径的和 sum 满足了要求（例如 sum == n），此时会将当前路径 path 加入到结果集 result 中，并进行回溯操作。
回溯操作包括将当前操作的影响从当前路径和当前状态中撤销，以便尝试其他可能的路径组合。
递归调用结束后的回溯：

在递归调用中，当完成了对当前数字的处理后（通常是尝试加入当前数字并递归处理下一个数字），会进行回溯操作。（！！！！这里很重要，在打日志时就可以看到回溯是如何进行的了）
这种情况下，回溯操作是为了确保在递归返回到当前层级时，状态已经被恢复到递归前的状态，从而可以尝试其他可能的数字组合。
在具体的实现中，回溯操作通常包括以下步骤：

····加入当前选择：将当前数字加入到路径 path 中，并更新当前的和 sum。
····递归处理：递归调用下一层级处理下一个数字。
····回溯：在递归调用返回后，撤销当前数字的选择，将其从路径 path 中移除，并恢复当前的和 sum 到递归前的状态。
回溯操作的发生时机是保证算法能够在所有可能的路径中搜索，并且在满足条件或者确定无法满足条件时及时回溯，以尝试其他可能的组合。

以本题为例子理解的回溯过程。

acm模式代码如图

#include <iostream>
#include <vector>using namespace std;vector<vector<int>> result;
vector<int> path;void backtracking(int k, int n, int sum, int startindex) {if (sum > n)return;if (path.size() == k) {if (sum == n) {result.push_back(path);cout << "存入一条路径" << endl;}return;}for (int i = startindex; i <= 9; i++) {sum += i;path.push_back(i);cout << "路径加入一个数" << endl;backtracking(k, n, sum, i + 1);// 回溯操作sum -= i;path.pop_back();cout << "撤销操作，回溯到上一个状态，寻找其他数字组合" << endl;}
}vector<vector<int>> combinationSum3(int k, int n) {result.clear();path.clear();cout << "调用combinationSum3函数" << endl;backtracking(k, n, 0, 1);return result;
}int main() {int k, n;// 从标准输入读取数据while (cin >> k >> n) {result = combinationSum3(k, n);// 输出结果for (const auto& combination : result) {for (int num : combination) {cout << num << " ";}cout << endl;}}return 0;
}

 日志如图：

可以看出，找到第一条路径后，就开始剪枝操作了。 

从这里开始，有两条一模一样的撤销操作和加入数的操作。证明一个数字和它的所有组合已经遍历完了。将从第二个数字开始查找符合条件的组合。 

如果有第二条路径的话

路径加入一个数
路径加入一个数
开始剪枝
撤销操作，回溯到上一个状态，寻找其他数字组合
路径加入一个数
开始剪枝
撤销操作，回溯到上一个状态，寻找其他数字组合
路径加入一个数
开始剪枝
撤销操作，回溯到上一个状态，寻找其他数字组合
路径加入一个数
开始剪枝
撤销操作，回溯到上一个状态，寻找其他数字组合
路径加入一个数
开始剪枝
撤销操作，回溯到上一个状态，寻找其他数字组合
路径加入一个数
开始剪枝
撤销操作，回溯到上一个状态，寻找其他数字组合
路径加入一个数
开始剪枝
撤销操作，回溯到上一个状态，寻找其他数字组合
撤销操作，回溯到上一个状态，寻找其他数字组合
路径加入一个数
路径加入一个数
开始剪枝
撤销操作，回溯到上一个状态，寻找其他数字组合
路径加入一个数
开始剪枝
撤销操作，回溯到上一个状态，寻找其他数字组合
路径加入一个数
开始剪枝
撤销操作，回溯到上一个状态，寻找其他数字组合
路径加入一个数
开始剪枝
撤销操作，回溯到上一个状态，寻找其他数字组合
路径加入一个数
开始剪枝
撤销操作，回溯到上一个状态，寻找其他数字组合
路径加入一个数
开始剪枝
撤销操作，回溯到上一个状态，寻找其他数字组合
撤销操作，回溯到上一个状态，寻找其他数字组合
路径加入一个数
路径加入一个数
开始剪枝
撤销操作，回溯到上一个状态，寻找其他数字组合
路径加入一个数
开始剪枝
撤销操作，回溯到上一个状态，寻找其他数字组合
路径加入一个数
开始剪枝
撤销操作，回溯到上一个状态，寻找其他数字组合
路径加入一个数
开始剪枝
撤销操作，回溯到上一个状态，寻找其他数字组合
路径加入一个数
开始剪枝
撤销操作，回溯到上一个状态，寻找其他数字组合
撤销操作，回溯到上一个状态，寻找其他数字组合
路径加入一个数
开始剪枝
撤销操作，回溯到上一个状态，寻找其他数字组合
路径加入一个数
开始剪枝
撤销操作，回溯到上一个状态，寻找其他数字组合
路径加入一个数
开始剪枝
撤销操作，回溯到上一个状态，寻找其他数字组合
路径加入一个数
开始剪枝
撤销操作，回溯到上一个状态，寻找其他数字组合
路径加入一个数
开始剪枝
撤销操作，回溯到上一个状态，寻找其他数字组合
1 3

 

剪枝情况

 在递归函数开头剪枝（好

if (sum > targetSum) { // 剪枝操作return;
}

17.电话号码的字母组合

题目：17. 电话号码的字母组合 - 力扣（LeetCode）

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。

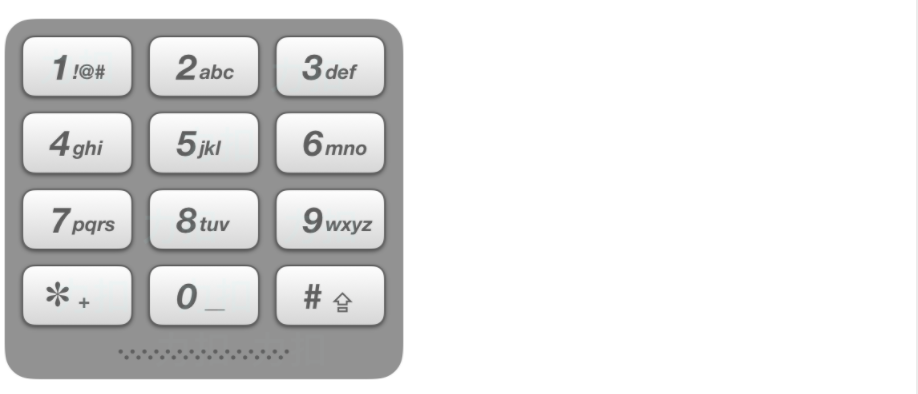
给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例:

• 输入："23"
• 输出：["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].

说明：尽管上面的答案是按字典序排列的，但是你可以任意选择答案输出的顺序

思路

 回溯的树形结构理解

深度是用户按键的digit长度，如例子中就是2.递归函数有一个参数index。。这个index是记录遍历第几个数字了，就是用来遍历digits的（题目中给出数字字符串），同时index也表示树的深度。

而横向遍历的宽度，即for循环次数获取到的所有结果集。

代码

class Solution {private://键盘按键数字和字母的映射const string letterMap[10] = {"", // 0"", // 1"abc", // 2"def", // 3"ghi", // 4"jkl", // 5"mno", // 6"pqrs", // 7"tuv", // 8"wxyz", // 9};
public:vector<string>result;string s;void backtraking(const string& digits,int index){if(index==digits.size())//当 index 达到 digits.size() 时，说明已经遍历完所有的数字，将当前的组合 s 添加到 result 中，然后返回。{result.push_back(s);return;}int digit=digits[index]-'0';//string类型转intstring letters=letterMap[digit];for(int i=0;i<letters.size();i++){s.push_back(letters[i]);backtraking(digits,index+1);//探索下一层数字对应的字母了s.pop_back();//回溯，在递归返回后，通过 s.pop_back() 撤销之前的选择，尝试其他字母组合。}}vector<string> letterCombinations(string digits) {result.clear();if(digits.size()==0)return result;backtraking(digits,0);return result;}
};

我的疑惑：index不会递增下去吗？

回溯的执行过程和 index 的变化

以 digits = "23" 为例，递归处理时的 index 变化如下：

1. 初始调用 backtracking("23", 0):

   • index = 0，处理 digits[0] = '2'，对应的字母是 "abc"。
   • 第一个递归调用：选择 'a'，调用 backtracking("23", 1)。

2. 递归调用 backtracking("23", 1):

   • index = 1，处理 digits[1] = '3'，对应的字母是 "def"。
   • 第一个递归调用：选择 'd'，调用 backtracking("23", 2)。

3. 递归调用 backtracking("23", 2)：

   • 此时 index = 2，已经达到了 digits.size()，所以将当前组合 "ad" 加入结果 result 中，并返回。
   • 这里 index 不再继续增加，而是返回到上一层（backtracking("23", 1)）。

4. 回溯到 backtracking("23", 1)：

   • 从组合 "ad" 中撤销 'd'，并选择下一个字母 'e'，继续递归调用 backtracking("23", 2)。

5. 递归调用 backtracking("23", 2)：

   • 再次达到 index = 2，组合 "ae" 加入结果，并返回到上一层。

6. 继续回溯：撤销 'e'，选择 'f'，重复上述过程，将 "af" 加入结果。

7. 完全处理完 'a' 后，回到 backtracking("23", 0)：

   • 撤销 'a'，选择 'b'，重复上述过程，处理 "bd", "be", "bf"。

8. 最后处理 'c'，得到 "cd", "ce", "cf"。

为什么 index 不会一直递增？

1. 每次递归调用时，index 加 1，是为了处理下一个数字对应的字母组合。
2. 当递归返回时，index 会回到上一层，并且回到上一层的状态后，会尝试其他的可能性（选择下一个字母），然后再进行递归处理。
3. 每次递归到达终点（即 index == digits.size()）时，递归结束，将当前的路径结果存入 result，接着回溯撤销选择，并返回上一层。

一些写法，是把回溯的过程放在递归函数里了

如for循环变成了这样，相应的，递归参数多了个string s，初始值是“”

 for (int i = 0; i < letters.size(); i++) {getCombinations(digits, index + 1, s + letters[i]); 

 这里隐藏了回溯的写法。

要彻底理解回溯的过程，可以自己打下日志，逐行看下代码进行过程。