一入递归深似海,算法之美无止境
最近在刷leetcode hot100,在写二叉树中最大路径和的时候,看到了一个佬对递归的理解,深受启发,感觉自己对于递归的题又行了!!!
这里给大家分享一下(建立大家先去尝试一下这道题再来看
124. 二叉树中的最大路径和
二叉树中的 路径 被定义为一条节点序列,序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。
路径和 是路径中各节点值的总和。
给你一个二叉树的根节点 root ,返回其 最大路径和 。
示例 1:
输入:root = [1,2,3] 输出:6 解释:最优路径是 2 -> 1 -> 3 ,路径和为 2 + 1 + 3 = 6
示例 2:
输入:root = [-10,9,20,null,null,15,7] 输出:42 解释:最优路径是 15 -> 20 -> 7 ,路径和为 15 + 20 + 7 = 42
提示:
- 树中节点数目范围是
[1, 3 * 104] -1000 <= Node.val <= 1000
ps:这道题感觉达不到困难的级别
但佬的解题思路就是清晰,让人豁然开朗,顿悟的不仅是这道题,而是递归
这道题说难也不难,但说容易也真不是那么容易能想到的(写得比较多,但都是心得,耐心看完就更上一层楼了)。 首先就是递归的方式,很多人都对递归一头雾水,一看就会,一写就废。不用担心,这是正常现象。 下面,我们详细解释一下这道题,顺便疏通一下递归的基本思路。
我们不要先去考虑整个递归的代码怎么去写,而是要明确一个递归的主体,就是这个递归的主体要怎么构造,然后再去想边界条件,返回值等等。
1、那么,首先我们可以假设走到了某个节点,现在要面临的问题是路径的最大值问题,显然对于这种问题,每遍历到一个节点,我们都要求出包含该节点在内的此时的最大路径,并且在之后的遍历中更新这个最大值。对于该节点来说,它的最大路径currpath就等于左右子树的最大路径加上本身的值,也就是currpath = left+right+node,val,但是有一个前提,我们要求的是最大路径,所以若是left或者right小于等于0了,那么我们就没有必要把这些值加上了,因为加上一个负数,会使得最大路径变小。这里的最大路径中的最其实就是一个限定条件,也就是我们常说的贪心算法,只取最大,最好,其余的直接丢弃。
2、好了,1中的主体我们已经明确了,但是还存在一个问题,那就是left和right具体应该怎么求,也就是left和right的递归形式。显然我们要把node.left和node.right再次传输到递归函数中,重复上述的操作。但如果到达了叶子节点,是不是需要往上一层返回了呢?那么返回值又是多少呢? 我们要明确left和right的基本含义,它们表示的是最大贡献,那么一个节点的最大贡献就等于node.val+max(left,right),这个节点本身选上,然后从它的左右子树中选择最大的那个加上。 对于叶子节点也是这样,但是叶子节点的左右子树都为空,所以加上0,哎,注意看,此时是不是边界条件也出来了,当节点为空时,返回0 。 好了,至此循环的主体,返回值,边界条件都定义好了,那么整个递归的代码是不是就水到渠成了。这样一看递归也没什么了不起的!!!
ps:除了向下思考,其实也可以向上思考,比如还是遍历到了某个节点,那么这个节点向上一层走,是不是要有一个返回值呢,那么返回值是什么呢?是不是和自己原来需要的right(or left)相同,只不过现在轮到自己了,自己原来需要最大贡献,那么此时返回时就返回最大贡献,自己的最大贡献不就是node.val+max(left,right)。就像是老板一层一层的压榨员工一样。
看完这些我结合我的AI做了一个总结: 嗯,也是对这道题的一个交代吧
在递归类的题目中,可能很多人都和我一样会感到困惑,尤其是写递归的过程中常常遇到“会看不会写”的窘境。递归的本质看似简单,但在实际应用中却往往让人抓不住重点。然而,解答这类题目的关键在于理清递归的基本框架与思维路径,而一旦掌握了这个过程,递归将不再神秘。
递归的困境:一看就会,一写就废
在初学递归时,我想大家都会有一种“知道大概,但无从下手”的感觉。这是因为递归不同于其他常规的解题思路,它往往需要我们站在一个较高的抽象层次去思考问题的整体,而不是仅仅关注细节。尤其是递归中“自我调用”的特性,让人很容易在一开始时就迷失在代码的具体实现中,而忽略了逻辑上的整体构建。
解题的核心思路:先明确递归的主体
要想解决递归类问题,首先必须放下对代码细节的焦虑,回到问题本身。一个清晰的递归思路,通常可以归纳为几个关键点:递归的主体是什么?边界条件是什么?返回值是什么?这几个问题解决后,递归的代码往往也就顺理成章了。
在这道题中,我们的目标是找到一条路径的最大值。那么,这里的递归主体可以这样定义:我们在每个节点上求解“从当前节点出发,经过该节点的最大路径值”,而这一最大路径值是由当前节点的值加上它的左右子树的最大路径值之和来确定的。然而,如果左右子树的某个最大路径值为负数,显然它对我们整体路径的贡献是负的,故我们应该舍弃这些负贡献,而仅取正值部分。这其实隐含了一种贪心算法的思路:在每次递归中,我们只选择对整体有利的子路径,而放弃那些对整体无益的部分。
递归的层次结构:从上到下的自我调用
接下来,我们需要思考左右子树的最大路径值如何求解。这其实就是递归的核心——我们将问题递归分解为更小的子问题,通过不断地递归调用自身,最终在叶子节点时触发递归的终止条件。在这道题中,递归的终止条件非常自然:当我们到达叶子节点的左右子树为空时,最大路径值为0。通过这样的层层递归,最后回溯时将每个节点的最大路径值传递回去,形成了完整的递归过程。
递归的回溯:每个节点的最大贡献
在递归过程中,我们不仅向下遍历,也需要向上回溯。在每次递归回溯时,我们需要将当前节点的“最大贡献”值返回给它的上一级节点,而这个最大贡献值正是当前节点的值加上左右子树中较大的那一部分。这就像是从员工到老板逐层递交成果,老板需要下属的最大贡献,而下属则将其最佳的工作结果汇报给老板。最终,通过逐层回溯,每一层都只保留了最佳的路径贡献,从而得到了全局的最优解。
总结
递归的美妙之处在于它让问题的层次结构清晰明了。通过递归,我们不仅可以将复杂的问题逐步拆解,还能在边界条件明确的情况下逐步解决每一层次的子问题。而这种由内而外的层层递归、由下而上的逐步回溯,使得递归问题不仅在形式上简洁优美,也在逻辑上充满了挑战与成就感。写好递归的关键并不在于一开始就写出完整的代码,而在于明确递归的主体,理解问题的层次结构,顺其自然地将边界条件、返回值、递归过程一一定义出来。这样一来,递归问题自然就迎刃而解了。
相关文章:

一入递归深似海,算法之美无止境
最近在刷leetcode hot100,在写二叉树中最大路径和的时候,看到了一个佬对递归的理解,深受启发,感觉自己对于递归的题又行了!!! 这里给大家分享一下(建立大家先去尝试一下这道题再来看 124. 二叉树中的最大路径和 二叉树中的 路径 被定义为一条节点序列,序列中每…...

进程的状态的理解(概念+Linux)
文章目录 进程的状态并行和并发物理和逻辑 时间片进程具有独立性等待的本质运行阻塞标记挂起等待 Linux下的进程状态(一)运行状态(R - running)(二)睡眠状态(S - sleeping)ÿ…...

Apache Linkis + OceanBase:如何提升数据分析效率
计算中间件 Apache Linkis 构建了一个计算中间件层,以实现上层应用程序和底层数据引擎之间的连接、治理和编排。目前,已经支持通过数据源的功能,实现用户通过Linkis 对接并使用 OceanBase数据库。 本文详细阐述了在 Apache Linkis v1.3.2中&a…...
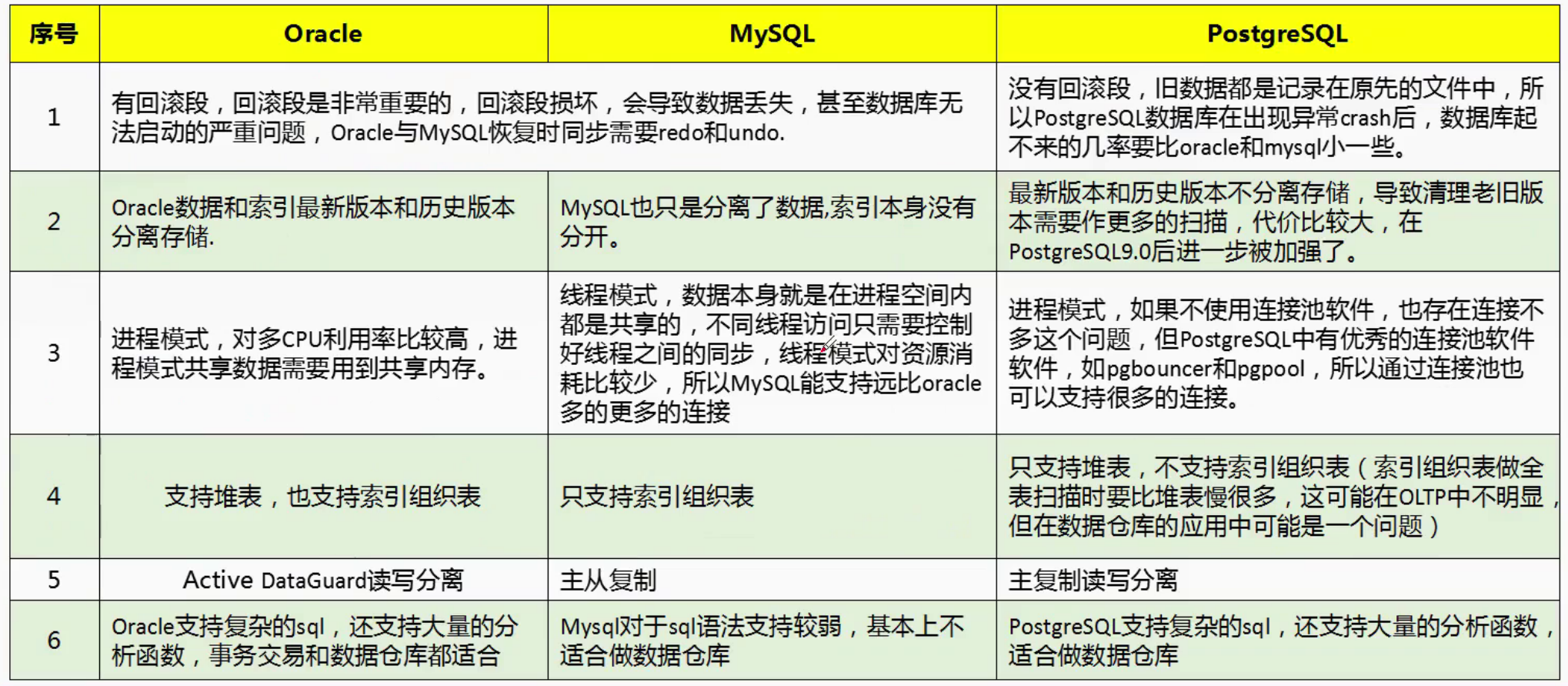
Day01-postgresql数据库基础入门培训
Day01-postgresql数据库基础入门培训 1、PostgresQL数据库简介2、PostgreSQL行业生态应用3、PostgreSQL版本发展与特性4、PostgreSQL体系结构介绍5、PostgreSQL与MySQL的区别6、PostgreSQL与Oracle、MySQL的对比 1、PostgresQL数据库简介 PostgreSQL【简称:PG】是加…...

打卡第四天 P1081 [NOIP2012 提高组] 开车旅行
今天是我打卡第四天,做个省选/NOI−题吧(#^.^#) 原题链接:[NOIP2012 提高组] 开车旅行 - 洛谷 题目描述 输入格式 输出格式 输入输出样例 输入 #1 4 2 3 1 4 3 4 1 3 2 3 3 3 4 3 输出 #1 1 1 1 2 0 0 0 0 0 输入 #2 10 4 5 6 1 …...

Jenkins Pipline流水线
提到 CI 工具,首先想到的就是“CI 界”的大佬--]enkjns,虽然在云原生爆发的年代,蹦出来了很多云原生的 CI 工具,但是都不足以撼动 Jenkins 的地位。在企业中对于持续集成、持续部署的需求非常多,并且也会经常有-些比较复杂的需求,此时新生的 CI 工具不足以支撑这些很…...

鸿蒙harmonyos next flutter混合开发之开发FFI plugin
创建FFI plugin summation,默认创建的FFI plugin是求两个数的和 flutter create --templateplugin_ffi summation --platformsandroid,ios,ohos 创建my_application flutter create --org com.example my_application 在my_application项目中文件pubspec.yaml引…...

oracle数据库安装和配置
Oracle数据库安装 一、安装前的准备 系统要求: 硬件:内存至少1GB(推荐2GB以上),硬盘至少10GB的可用空间,CPU至少2核心。 操作系统:支持Oracle版本的Windows(如Windows 10或更高版本…...

猫玖破密啦
题目: 终究还是猫哥:3d5a3a0cfff7fb2e29194c0b7a89f284ff19a8 玖离:收到消息Oh,what_is_the_flag 玖离:7468655f666c61675f69735f666c13556d2cf2faec1e2d0f330b7dcceea1c62cb2 终究还是猫哥:收到消息************************************ 已…...

SpringBoot框架:服装生产管理的现代化工具
摘 要 本协力服装厂服装生产管理系统设计目标是实现协力服装厂服装生产的信息化管理,提高管理效率,使得协力服装厂服装生产管理作规范化、科学化、高效化。 本文重点阐述了协力服装厂服装生产管理系统的开发过程,以实际运用为开发背景&#…...

Android Preference的使用以及解析
简单使用 values.arrays.xml <?xml version"1.0" encoding"utf-8"?> <resources><string-array name"list_entries"><item>Option 1</item><item>Option 2</item><item>Option 3</item&…...

HCIP——GRE和MGRE
目录 VPN GRE GRE环境的搭建 GRE的报文结构 GRE封装和解封装报文的过程 GRE配置编辑 R1 R2 GRE实验编辑 MGRE 原理 MGRE的配置 R1 R2 R3 R4 查看映射表 抓包 MGRE环境下的RIP网络 综合练习编辑 VPN 说到GRE,我们先来说个大…...

微信小程序——音乐播放器
一、界面设计 播放页面: 显示当前播放歌曲的封面图片、歌曲名称、歌手名称。有播放 / 暂停按钮、上一首、下一首按钮。进度条显示播放进度,可以拖动进度条调整播放位置。音量调节滑块。 歌曲列表页面: 展示歌曲列表,包括歌曲名称、…...

OceanBase 4.x 部署实践:如何从单机扩展至分布式部署
OceanBase 4.x 版本支持2种部署模式:单机部署与分布式部署,同时支持从单机平滑扩展至分布式架构。这样,可以有效解决小型业务向大型业务转型时面临的扩展难题,降低了机器资源的成本。 以下将详述如何通过命令行,实现集…...

大数据新视界 --大数据大厂之TeZ 大数据计算框架实战:高效处理大规模数据
💖💖💖亲爱的朋友们,热烈欢迎你们来到 青云交的博客!能与你们在此邂逅,我满心欢喜,深感无比荣幸。在这个瞬息万变的时代,我们每个人都在苦苦追寻一处能让心灵安然栖息的港湾。而 我的…...
)
docker详解介绍+基础操作 (三)
1.docker 存储引擎 Overlay: 一种Union FS文件系统,Linux 内核3.18后支持 Overlay2:Overlay的升级版,docker的默认存储引擎,需要磁盘分区支持d-type功能,因此需要系统磁盘的额外支持。 关于 d-type 传送…...

【大语言模型-论文精读】谷歌-BERT:用于语言理解的预训练深度双向Transformers
【大语言模型-论文精读】谷歌-BERT:用于语言理解的预训练深度双向Transformers 目录 文章目录 【大语言模型-论文精读】谷歌-BERT:用于语言理解的预训练深度双向Transformers目录0. 引言1. 简介2 相关工作2.1 基于特征的无监督方法2.2 无监督微调方法2.3…...

【Java】集合中单列集合详解(一):Collection与List
目录 引言 一、Collection接口 1.1 主要方法 1.1.1 添加元素 1.1.2 删除元素 1.1.3 清空元素 1.1.4 判断元素是否存在 1.1.5 判断是否为空 1.1.6 求取元素个数 1.2 遍历方法 1.2.1 迭代器遍历 1.2.2 增强for遍历 1.2.3 Lambda表达式遍历 1.2.4 应用场景 二、…...

【Fine-Tuning】大模型微调理论及方法, PytorchHuggingFace微调实战
Fine-Tuning: 大模型微调理论及方法, Pytorch&HuggingFace微调实战 文章目录 Fine-Tuning: 大模型微调理论及方法, Pytorch&HuggingFace微调实战1. 什么是微调(1) 为什么要进行微调(2) 经典简单例子:情感分析任务背景微调 (3) 为什么微调work, 理论解释下 2…...
清华系“仓颉”来袭:图形起源:用AI颠覆字体设计,推动大模型商业化落地
大模型如何落地?又该如何实现商业化?这一议题已成为今年科技领域的焦点话题。 在一个鲜为人知的字体设计赛道上,清华创业公司“图形起源”悄然实现了商业变现:他们帮助字体公司将成本降低了80%,生产速度提升了10倍以上…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...

RushDB开源程序 是现代应用程序和 AI 的即时数据库。建立在 Neo4j 之上
一、软件介绍 文末提供程序和源码下载 RushDB 改变了您处理图形数据的方式 — 不需要 Schema,不需要复杂的查询,只需推送数据即可。 二、Key Features ✨ 主要特点 Instant Setup: Be productive in seconds, not days 即时设置 :在几秒钟…...
)
背包问题双雄:01 背包与完全背包详解(Java 实现)
一、背包问题概述 背包问题是动态规划领域的经典问题,其核心在于如何在有限容量的背包中选择物品,使得总价值最大化。根据物品选择规则的不同,主要分为两类: 01 背包:每件物品最多选 1 次(选或不选&#…...

「Java基本语法」变量的使用
变量定义 变量是程序中存储数据的容器,用于保存可变的数据值。在Java中,变量必须先声明后使用,声明时需指定变量的数据类型和变量名。 语法 数据类型 变量名 [ 初始值]; 示例:声明与初始化 public class VariableDemo {publi…...
——统计抽样学习笔记(考试用))
统计学(第8版)——统计抽样学习笔记(考试用)
一、统计抽样的核心内容与问题 研究内容 从总体中科学抽取样本的方法利用样本数据推断总体特征(均值、比率、总量)控制抽样误差与非抽样误差 解决的核心问题 在成本约束下,用少量样本准确推断总体特征量化估计结果的可靠性(置…...
