信息学奥赛一本通 1347:【例4-8】格子游戏
【题目链接】
ybt 1347:【例4-8】格子游戏
【题目考点】
1. 并查集:判断无向图是否有环
【解题思路】
该题为判断无向图是否有环。可以使用并查集来完成。
学习并查集时,每个元素都由一个整数来表示。而该问题中每个元素是一个坐标点,由(x, y)两个整数构成。
因而有两种方法解决该问题
解法1:将二维坐标变为一个整数
通过一个公式将二维坐标换算为一个整数,用这个整数代表该二维坐标。
例:假设坐标点是2行3列的,每个位置的坐标为x, y,转变后的数字为d,记为(x, y):d
第1列 第2列 第3列 第1行 (1,1):1 (1,2):2 (1,3):3 第2行 (2,1):4 (2,2):5 (2,3):6
可以推出n行n列的坐标系中,坐标(x,y)转为数字d,公式为:d=(x−1)⋅n+yd=(x-1)\cdot n+yd=(x−1)⋅n+y
把每个坐标都用一个数字表示。
每输入一个坐标(x,y),求出其对应的数字f。
- 如果接下来输入字母D,即向下画,那么与(x,y)连接的点是(x+1, y),求出其对应的数字t。
- 如果接下来输入字母R,即向右画,那么与(x,y)连接的点是(x, y+1),求出其对应的数字t。
判断f和t是否在一个集合(连通子图)中
- 如果是,那么f与t连边会形成环,游戏结束。输出游戏结束时的步数。
- 否则把f和t所在的集合合并。
解法2:直接使用坐标作为并查集中的元素
如果并查集中的元素不为整数,可以将fa数组改为映射(map类型),同时find、merge都发生改变。
解题思路与解法1类似。
在输入时,使用find直接判断两个数对元素是否在一个集合中
- 如果已在一个集合中,说明两点间有路径连通,再加一条边就会形成环。
- 否则,使用merge把两个数对元素所在的集合进行合并。
【题解代码】
解法1:将二维坐标变为一个整数
#include<bits/stdc++.h>
using namespace std;
#define N 40005
int fa[N], n, m;
int getNum(int x, int y)//用1个数字代表二维的坐标点
{return (x-1)*n + y;
}
void init(int n)
{for(int i = 1; i <= n; ++i)fa[i] = i;
}
int find(int x)
{if(x == fa[x])return x;elsereturn fa[x] = find(fa[x]);
}
void merge(int x, int y)
{ fa[find(x)] = find(y);
}
int main()
{int x, y, i, f, t;char c;cin >> n >> m;init(n*n);for(i = 1; i <= m; ++i)//i:第几步 {cin >> x >> y >> c;f = getNum(x, y);if(c == 'D')t = getNum(x+1, y);else//c == 'R't = getNum(x, y+1);if(find(f) == find(t))break;elsemerge(f, t);}if(i <= m)cout << i;elsecout << "draw";return 0;
}
解法2:直接使用坐标作为并查集中的元素
#include<bits/stdc++.h>
using namespace std;
typedef pair<int, int> Pair;
map<Pair, Pair> fa;
Pair find(Pair x)
{if(x == fa[x])return x;elsereturn fa[x] = find(fa[x]);
}
void merge(Pair x, Pair y)
{fa[find(x)] = find(y);
}
int main()
{Pair p, q;int n, m, x, y;char c;cin >> n >> m;for(int i = 1; i <= m; ++i){cin >> x >> y >> c;p = Pair(x, y);if(c == 'D')q = Pair(x+1, y);else//c == 'R'q = Pair(x, y+1);if(fa.count(p) == 0)//如果不存在该点,则初始化 fa[p] = p;if(fa.count(q) == 0)fa[q] = q;if(find(p) == find(q))//p, q已连通,p,q再连边,则存在环 {cout << i;//输出步数 return 0;}merge(p, q);//合并两点 }cout << "draw";return 0;
}
相关文章:

信息学奥赛一本通 1347:【例4-8】格子游戏
【题目链接】 ybt 1347:【例4-8】格子游戏 【题目考点】 1. 并查集:判断无向图是否有环 【解题思路】 该题为判断无向图是否有环。可以使用并查集来完成。 学习并查集时,每个元素都由一个整数来表示。而该问题中每个元素是一个坐标点&a…...

acwing3417. 砝码称重
acwing3417. 砝码称重算法 1: DFS算法2 : DP算法 1: DFS /*** 数据范围 对于 50%的评测用例,1≤N≤15. 对于所有评测用例,1≤N≤100,N 个砝码总重不超过 1e5. */ /* 算法 1: DFS 思路 : 对于每个砝码,有放在左边,放在右边,和不放三种选择,使…...

生成式 AI:百度“文心一言”对标 ChatGPT?什么技术趋势促使 ChatGPT 火爆全网?
文章目录前言一、生成式 AI 的发展和现状1.1、什么是生成式 AI?1.2、生成式 AI 的发展趋势1.3、AI 生成内容的业务场景和分类二、生成式 AI 从分析领域到创作领域2.1、 降低内容创作门槛,增加 UGC 用户群体2.2、提升创作及反馈效率,铺垫线上实…...
PCL 非线性最小二乘法拟合圆柱
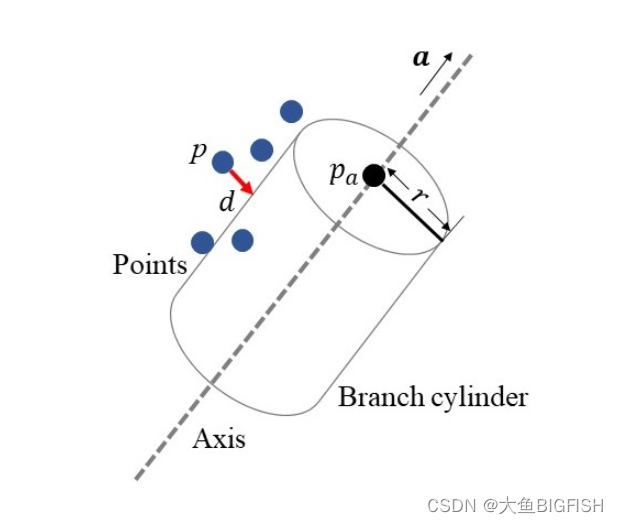
文章目录 一、简介二、实现代码三、实现效果参考资料一、简介 这里通过非线性最小二乘的方法来实现圆柱体的拟合,具体的计算过程如下所述: 图中, p p p为输入数据的点位置,求解的参数为柱体的轴向向量 a...
【设计模式】迪米特法则
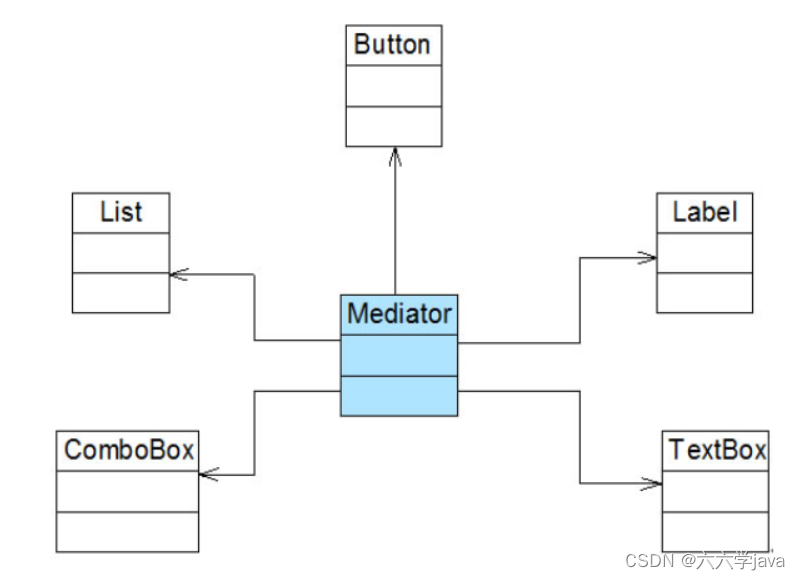
文章目录一、迪米特法则定义二、迪米特法则分析三、迪米特法则实例一、迪米特法则定义 迪米特法则(Law of Demeter, LoD):一个软件实体应当尽可能少地与其他实体发生相互作用。 二、迪米特法则分析 如果一个系统符合迪米特法则,那么当其中某一个模块发…...

CSS3笔试题精讲1
Q1 BFC专题 防止父元素高度坍塌 4种方案 父元素的高度都是由内部未浮动子元素的高度撑起的。 如果子元素浮动起来,就不占用普通文档流的位置。父元素高度就会失去支撑,也称为高度坍塌。 即使有部分元素留在普通文档流布局中支撑着父元素,如果浮动 起来的元素高度高于留下的…...
交叉编译用于移植的Qt库
前言 如果在Ubuntu上使用qt开发可移植到周立功开发板的应用程序,需要在Ubuntu上交叉编译用于移植的Qt库,具体做法如下: 1、下载源码 源码qt-everywhere-opensource-src-5.9.6.tar.xz拷贝到ubuntu自建的software文件下 2、解压 点击提取到此处 3、安装配置 运行脚本文…...

泰凌微TLSR8258 zigbee开发环境搭建
目录必备软件工具抓包分析辅助工具软件开发包PC 辅助控制软件 (ZGC)必备软件工具 下载地址:http://wiki.telink-semi.cn/ • 集成开发环境: TLSR8 Chips: Telink IDE for TC32 TLSR9 Chips: Telink RDS IDE for RISC-V • 下载调试工具: Telink Burning and Debugg…...

C#实现商品信息的显示异常处理
实验四:C#实现商品信息的显示异常处理 任务要求: 在进销存管理系统中,商品的库存信息有很多种类,比如商品型号、商品名称、商品库存量等。在面向对象编程中,这些商品的信息可以存储到属性中,然后当需要使…...
)
细数N个获取天气信息的免费 API ,附超多免费可用API 推荐(三)
前言 市面上有 N 多个查询天气信息的软件、小程序以及网页入口,基本都是通过调用天气查询 API 去实现的。 今天整理了一下多种场景的天气预报API 接口分享给大家,有需要赶紧收藏起来。 天气预报查询 天气预报查询支持全国以及全球多个城市的天气查询…...

20230404英语学习
今日单词 decade n.十年 allocate vt.分配,分派,把…拨给 compress v.压缩;缩短;浓缩 regenerate v.(使)复兴,(使)振兴;(使)再生 …...
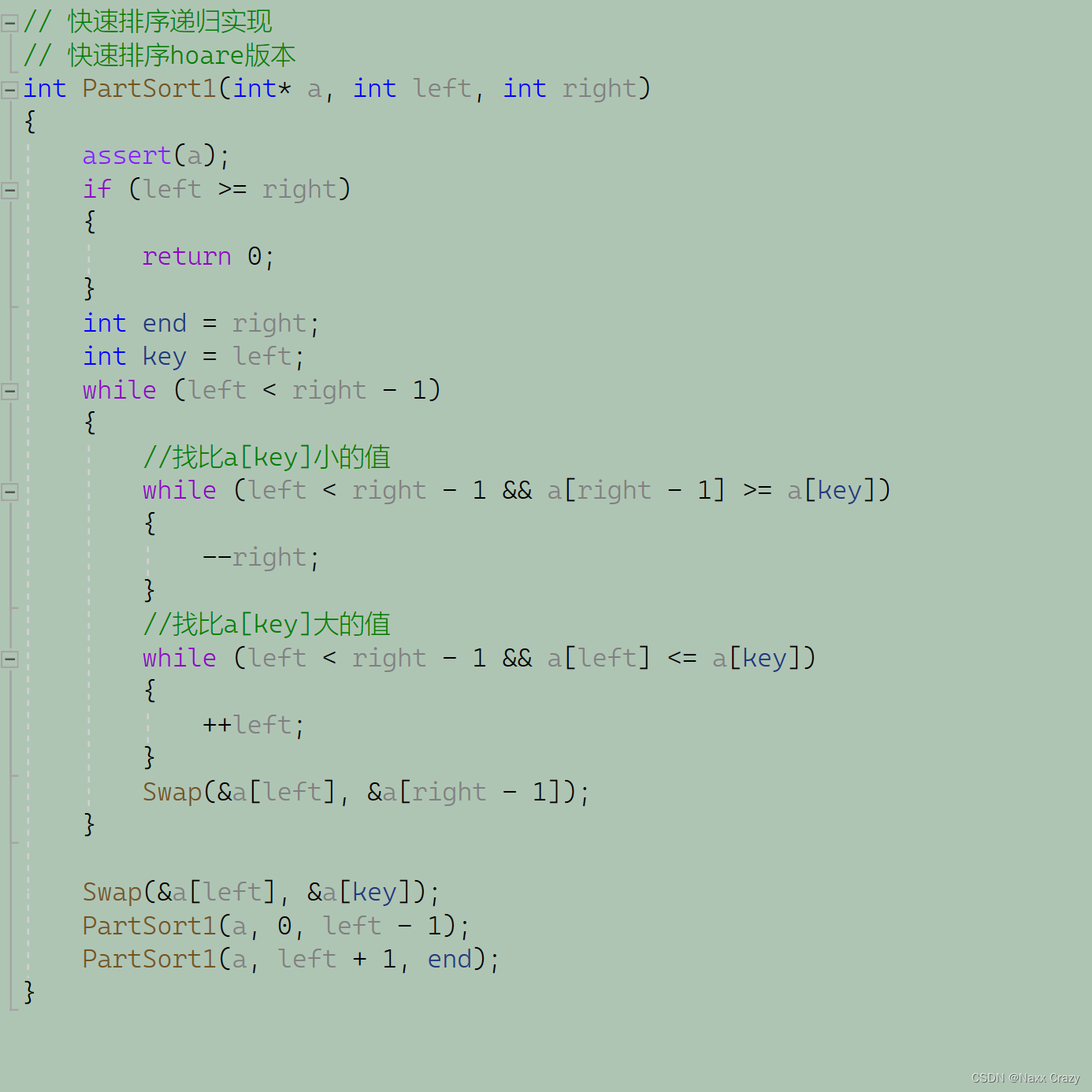
冒泡排序 快排(hoare递归)
今天要讲一个是冒泡排序,进一个是快排,首先是冒泡排序,我相信大家接触的第一个排序并且比较有用的算法就是冒泡排序了,冒泡排序是算法里面比较简单的一种,所以我们先看看一下冒泡排序 还是个前面一样,我们…...

49天精通Java,第24天,Java链表、散列表、HashSet、TreeSet
目录一、链表二、散列表三、HashSet四、TreeSet五、TreeSet常用方法大家好,我是哪吒。 一、链表 从数组中间删除一个元素开销很大,其原因是向数组中插入元素时,此元素之后的所有元素都要向后端移动,删除时也是,数组中…...

HashMap源码分析小结
HashMap相关问题 HashMap实现原理 HashMap是以键值对的形式存储数据,内部是通过数组链表结构实现,在1.7之后的版本,链表结构可以升级为红黑树,提高查询效率 key和value都支持为null;key为null时hash值是0࿰…...

太奇怪了!小公司面试全挂,大厂面试全过,为什么小公司要求比大厂还高?...
大厂的人才去小公司面试,一定是降维打击吗?还真未必。一位网友很困惑:真的奇怪,小公司面试全挂,大厂面试10个过了9个,感觉小公司要求比大厂还高,这是怎么了?来看看网友们的看法。有人…...

Java开发环境配置
Java开发环境配置 Java是目前世界上最流行的编程语言之一,它的使用范围广泛,从Web应用程序到桌面应用程序再到移动应用程序,Java都是一种非常有用的语言。想要进行Java开发,首先需要在计算机上配置Java开发环境。 在本文中&…...
大学英语视听说教程(陈向京版本)
词汇题(55道) 1. You should carefully think over_____ the manager said at the meeting. A. that B. which C. what D. whose 1.选C,考察宾语从句连接词,主句谓语动词think over后面缺宾语,后面的宾语从句谓语动…...

nginx--开源免费
nginx开源免费,支持高性能,高并发的web服务和代理服务软件。 apache,nodejs nginx可以提供的服务: 1、web服务 2、负载均衡(反向代理)(动静分离) 3、web cache(web缓存) nginx…...
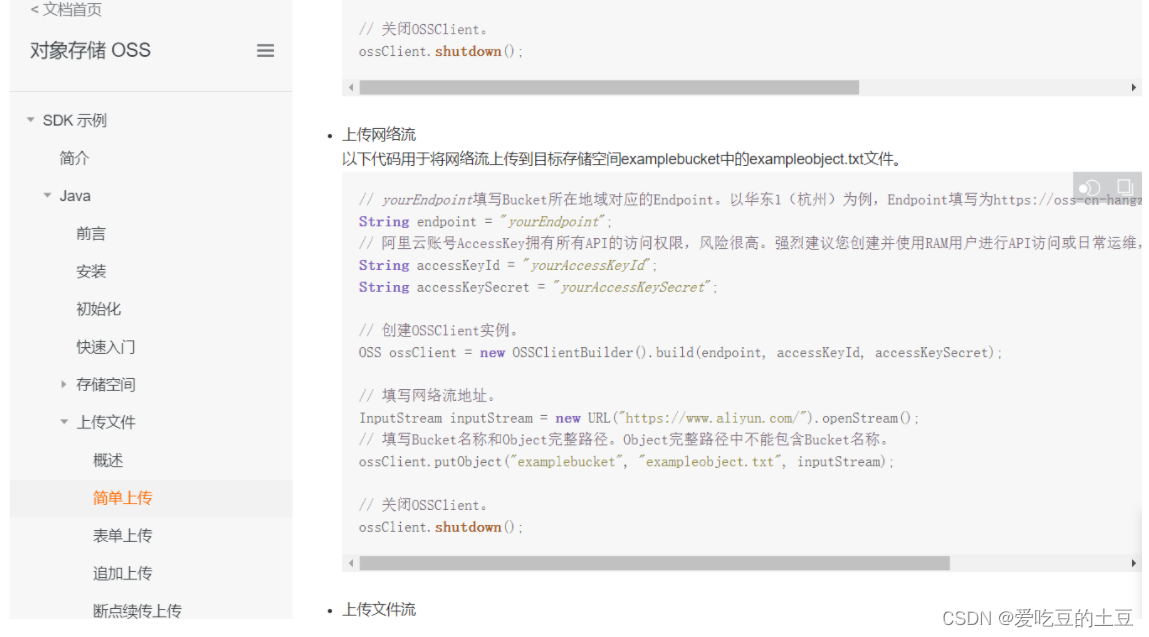
阿里云OSS对象存储
目录 1:OSS 1.1:开通OSS服务 1.2:搭建OSS环境 1.2.1:创建Bucket存储空间 1.2.2:创建文件夹上传图片 1.2.3:RAM访问控制 1.3:快速入门 1.3.1:下载SDK 1.3.2:搭建环…...
基于VHDL语言的汽车测速系统设计_kaic
摘 要 汽车是现代交通工具。车速是一项至关重要的指标。既影响着汽车运输的生产率,又关乎着汽车行驶有没有超速违章,还影响着汽车行驶时人们的人身安全。而伴随着我国国民的安全防范意识的逐步增强,人们也开始越来越关心因为汽车的超速而带来的极其严重…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...
