数据结构进阶:二叉搜索树_C++
目录
前言:
一、二叉搜索树
1.1二叉搜索树概念
2.2 二叉搜索树操作
1. 二叉搜索树的插入
1.1、插入过程
1.2、代码实现
2、二叉树的删除
2.1、结点删除情况
2.2、替换删除法
1、替换思路
2、代码实现:
3、二叉搜索树的查找
3.1、查找规则
3.2、代码实现
二、二叉搜索树的应用
1. K模型
2、KV模型
三、二叉搜索树的性能分析
前言:
1. map和set特性需要先铺垫二叉搜索树,而二叉搜索树也是一种树形结构
2. 二叉搜索树的特性了解,有助于更好的理解map和set的特性
3. 二叉树中部分面试题稍微有点难度,在前面讲解大家不容易接受,且时间长容易忘
4. 有些OJ题使用C语言方式实现比较麻烦,比如有些地方要返回动态开辟的二维数组,非常麻 烦。
一、二叉搜索树
1.1二叉搜索树概念
- 二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树

2.2 二叉搜索树操作
树的框架:
//结点
template<class K>
struct BSTreeNode
{BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;BSTreeNode(const K& key):_left(nullptr), _right(nullptr), _key(key){}
};
//二叉搜索树的操作
template<class K>
class BSTree
{typedef BSTreeNode<K> Node;
private:Node* _root = nullptr;
};
1. 二叉搜索树的插入
1.1、插入过程
插入的具体过程如下:
a. 树为空,则直接新增节点,赋值给root指针
b. 树不空,按二叉搜索树性质查找插入位置,插入新节点
解释:假设我们要插入16、0,那我们就要根据二叉搜索树的特点来进行判断,想要插入16,从根节点开始,如果比根节点大,那么就走右子树,继续比较。如果比根节点小,那么就走左子树继续比较

所以我们的插入功能应该如何写呢?
1.2、代码实现
bool Insert(const K& key)
{
//判断二叉树是否为空if (_root == nullptr){_root = new Node(key);return true;}Node* parent = nullptr;Node* cur = _root;
//进行插入while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{return false;}}
//找到插入位置,并新开辟一个结点cur = new Node(key);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;
}细节解释:
1、我们最开始需要判断二叉树是否为空,如果不判断,cur就为空,就不会进入循环判断的同时,之后parent指向结点为野指针,不安全
2、在我们循环判断时,需要记录cur的父节点,cur最终找到的是插入位置,如果我们想成功插入,那么就需要由该位置的父节点进行链接
2、二叉树的删除
2.1、结点删除情况
首先查找元素是否在二叉搜索树中,如果不存在,则返回, 否则要删除的结点可能分下面四种情 况:
a. 要删除的结点无孩子结点
b. 要删除的结点只有左孩子结点
c. 要删除的结点只有右孩子结点
d. 要删除的结点有左、右孩子结点
看起来有待删除节点有4中情况,实际情况a可以与情况b或者c合并起来,因此真正的删除过程如下:
情况a:直接删除
情况b:删除该结点且使被删除节点的双亲结点指向被删除节点的左孩子结点--直接删除
情况c:删除该结点且使被删除节点的双亲结点指向被删除结点的右孩子结点--直接删除
情况d:在它的右子树中寻找中序下的第一个结点(关键码最小),用它的值填补到被删除节点 中,再来处理该结点的删除问题--替换法删除
情况a、b、c都好理解,情况a直接删除即可,情况bc是让被删除结点的孩子去顶替它的位置即可
难的是情况d,当它有两个孩子时应该怎么去选择,我们所用到的替换法删除又是什么呢?
2.2、替换删除法
1、替换思路
我们所找的去替换被删除结点的值最重要的是能在该位置站得住脚---就是要比左孩子大,又要比右孩子小
那哪些结点能站得住脚呢?
是被删除结点的左子树的最大结点(右结点)或者右子树的最小结点(左结点)
怎么理解?我们知道,父结点的左子树上的值,都要比父结点小,父结点的右子树上的值,都要比父结点大。我们再拿父结点的左孩子来说,同理比它小的值也同样会走到它的左子树上,比它大的值也同样会走到它的右子树上。
那么我们就可以明白:被删除结点的左子树的最大右节或者右子树的最小左结点一定会比被删除结点的左孩子大,又比其右孩子小
这也是搜索二叉数的特征:一棵树的左子树的最右节点是左子树的最大结点,一棵树的右子树的最左结点是右子树的最小结点
另外需要注意的是,我们被删除结点的左子树的最大结点(右结点)或者右子树的最小结点(左结点是可以直接删除的,我们在上面已经分析过删除情况。
2、代码实现:
情况b、c再删除时又会遇到的情况:
1、被删除结点的左子树为空

假如我们要删除结点3,且被删除结点的左子树为空,我们被删除结点的父结点就要链接被删除结点的右子树
2、被删除结点的右子树为空

假如我们要删除结点3,且被删除结点的右子树为空,我们被删除结点的父结点就要链接被删除结点的左子树
情况d:
我们知道:
1、找被删除结点的左子树的最大右结点或者右子树的最左小结点(这个在后面的理解很重要!)
2、一棵树的左子树的最右节点是左子树的最大结点,一棵树的右子树的最左结点是右子树的最小结点
所以我们需要先找到一个能站得住脚的结点,我们就拿右子树的最小结点举例,将它命名为rightMin
我们找到rightMin再去将被删除结点与rightMin结点的值key交换,并且在找rightMin时再用一个中间变量rightMinParent去记录rightMin的父结点,最终在交换完key后我们需要删除交换后的rightMin就需要由父结点来链接。
此时又会遇到两种情况:
1、rightMin如果是父结点rightMinParent的左结点,我们就需要让rightMinParent去链接rightMin的右节点(如果存在即链接,不存在即为空)
2、1、rightMin如果是父结点rightMinParent的右结点,我们就需要让rightMinParent去链接rightMin的右节点(如果存在即链接,不存在即为空)
删除函数代码:
bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{// 删除// 左为空,父亲指向我的右// 先判断删除的是不是头结点if (cur->_left == nullptr){//if(parent == nullptr)if (cur == _root){_root = cur->_right;}else{if (cur == parent->_left){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}delete cur;}else if (cur->_right == nullptr){//if(parent == nullptr)if (cur == _root){_root = cur->_left;}else{// 右为空,父亲指向我的左if (cur == parent->_left){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}delete cur;}else{// 左右都不为空,替换法删除// // 查找右子树的最左节点替代删除Node* rightMinParent = cur;Node* rightMin = cur->_right;while (rightMin->_left){rightMinParent = rightMin;rightMin = rightMin->_left;}swap(cur->_key, rightMin->_key);if (rightMinParent->_left == rightMin)rightMinParent->_left = rightMin->_right;elserightMinParent->_right = rightMin->_right;delete rightMin;}return true;}}return false;}
3、二叉搜索树的查找
3.1、查找规则
a、从根开始比较,查找,比根大则往右边走查找,比根小则往左边走查找。
b、最多查找高度次,走到空,还没找到,这个值不存在
3.2、代码实现
bool Find(const K& key)
{Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return true;}}return false;
}二、二叉搜索树的应用
1. K模型
K模型即只有key作为关键码,结构中只需要存储Key即可,关键码即为需要搜索到 的值。
比如:给一个单词word,判断该单词是否拼写正确。
具体方式如下:
- 以词库中所有单词集合中的每个单词作为key,构建一棵二叉搜索树
- 在二叉搜索树中检索该单词是否存在,存在则拼写正确,不存在则拼写错误。
这个我们需要一个词库,所以我们在这里先不做这个实现,我们用KV模型来实现
2、KV模型
每一个关键码key,都有与之对应的值Value,即的键值对。该种方 式在现实生活中非常常见:
- 比如英汉词典就是英文与中文的对应关系,通过英文可以快速找到与其对应的中文,英 文单词与其对应的中文就构成一种键值对;
- 再比如统计单词次数,统计成功后,给定单词就可快速找到其出现的次数,单词与其出 现次数就是就构成一种键值对。
我们先将KV模型代码写出来:
namespace key_value
{template<class K, class V>struct BSTreeNode{BSTreeNode<K, V>* _left;BSTreeNode<K, V>* _right;K _key;V _value;// pair<K, V> _kv;BSTreeNode(const K& key, const V& value):_left(nullptr), _right(nullptr), _key(key), _value(value){}};template<class K, class V>class BSTree{typedef BSTreeNode<K, V> Node;public:// logNbool Insert(const K& key, const V& value){if (_root == nullptr){_root = new Node(key, value);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(key, value);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return cur;}}return cur;}bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{// 删除// 左为空,父亲指向我的右if (cur->_left == nullptr){//if(parent == nullptr)if (cur == _root){_root = cur->_right;}else{if (cur == parent->_left){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}delete cur;}else if (cur->_right == nullptr){//if(parent == nullptr)if (cur == _root){_root = cur->_left;}else{// 右为空,父亲指向我的左if (cur == parent->_left){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}delete cur;}else{// 左右都不为空,替换法删除// // 查找右子树的最左节点替代删除Node* rightMinParent = cur;Node* rightMin = cur->_right;while (rightMin->_left){rightMinParent = rightMin;rightMin = rightMin->_left;}swap(cur->_key, rightMin->_key);if (rightMinParent->_left == rightMin)rightMinParent->_left = rightMin->_right;elserightMinParent->_right = rightMin->_right;delete rightMin;}return true;}}return false;}void InOrder(){_InOrder(_root);cout << endl;}private:void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << ":" << root->_value << endl;_InOrder(root->_right);}private:Node* _root = nullptr;};这也只是在我们原先实现的基础上做改动。
示例一:翻译单词
void TestBSTree2()
{BSTree<string, string> dict;dict.Insert("string", "字符串");dict.Insert("left", "左边");dict.Insert("insert", "插入");//...string str;while (cin >> str){BSTreeNode<string, string>* ret = dict.Find(str);if (ret){cout << ret->_value << endl;}else{cout << "无此单词,请重新输入" << endl;}}
}示例二:计数
void TestBSTree3(){// 统计次数string arr[] = { "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜",
"苹果", "香蕉", "苹果", "香蕉","苹果","草莓", "苹果","草莓"};BSTree<string, int> countTree;for (const auto& str : arr){auto ret = countTree.Find(str);if (ret == nullptr){countTree.Insert(str, 1);}else{ret->_value++;}}countTree.InOrder();}
}三、二叉搜索树的性能分析
插入和删除操作都必须先查找,查找效率代表了二叉搜索树中各个操作的性能。
对有n个结点的二叉搜索树,若每个元素查找的概率相等,则二叉搜索树平均查找长度是结点在二 叉搜索树的深度的函数,即结点越深,则比较次数越多。
但对于同一个关键码集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树:

最优情况下,二叉搜索树为完全二叉树(或者接近完全二叉树),其平均比较次数为:$log_2 N$
最差情况下,二叉搜索树退化为单支树(或者类似单支),其平均比较次数为:$\frac{N}{2}$
相关文章:

数据结构进阶:二叉搜索树_C++
目录 前言: 一、二叉搜索树 1.1二叉搜索树概念 2.2 二叉搜索树操作 1. 二叉搜索树的插入 1.1、插入过程 1.2、代码实现 2、二叉树的删除 2.1、结点删除情况 2.2、替换删除法 1、替换思路 2、代码实现: 3、二叉搜索树的查找 3.1、查找规则 …...

uni-app之旅-day04-商品列表
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言6. 商品列表6.0 创建 goodslist 分支6.1 定义请求参数对象6.2 获取商品列表数据6.3 渲染商品列表结构6.4 把商品 item 项封装为自定义组件在 goods_detail 组件…...

单元测试的定义
概念 单元测试是对软件中的最小可测试单元进行检查和验证的过程。在面向对象编程中,最小可测试单元通常是一个方法或者一个类。它的目的是隔离各个部分的代码,确保每个单元都能按预期工作,从而提高软件的质量和可维护性。重要性 发现早期错误…...
)
C语言从头学66—学习头文件 <stdio.h>(二)
关于可变参数,我们曾经在《C语言从头学27》中接触过,下面学习能够接收可变参数作为 参数的几个函数。 一、printf函数的能够接收可变参数的变体函数: 1、函数vprintf() 功能:按照给定格式,将可变参数中的内容输…...

python静默活体检测接口集成-人脸识别API-人脸认证
静默活体检测是一种不需要用户主动配合(如眨眼、点头等)的活体检测技术,通常通过摄像头采集用户的人脸图像,结合计算机视觉与AI算法来判断用户是否为真人。这项技术被广泛应用于身份验证、金融交易安全、智能门禁等领域。 确定接口…...
Ubuntu安装nvidia显卡驱动
一、安装依赖 1、更新 sudo apt update sudo apt upgrade -y 2、基础工具 sudo apt install -y build-essential cmake 图形界面相关 sudo apt install -y lightdm 注:在弹出对话框选择"lightdm" 下载nvidia驱动: 进入如下网址:http…...
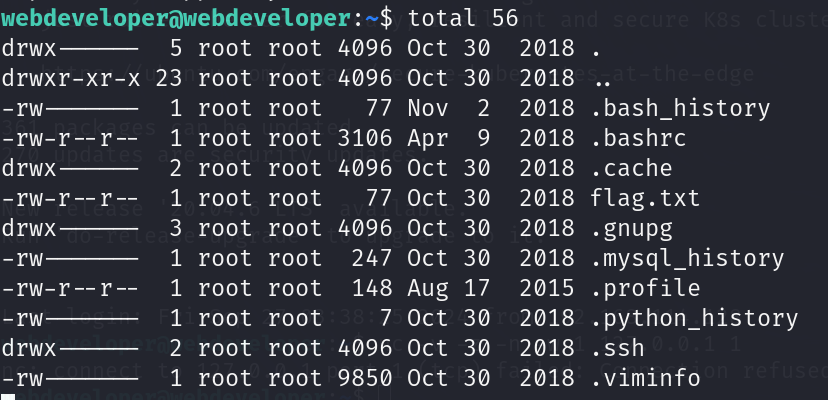
vulnhub-Web Developer 1靶机
vulnhub:Web Developer: 1 ~ VulnHub 导入靶机,放在kali同网段,扫描 靶机在192.168.114.129,扫描端口 有网站服务,访问 没什么东西,扫目录 真不少,访问一下,也只是一些普通的Wordpr…...

安全帽头盔检测数据集 3类 12000张 安全帽数据集 voc yolo
安全帽头盔检测数据集 3类 12000张 安全帽数据集 voc yolo 安全帽头盔检测数据集介绍 数据集名称 安全帽头盔检测数据集 (Safety Helmet and Person Detection Dataset) 数据集概述 该数据集专为训练和评估基于YOLO系列目标检测模型(包括YOLOv5、YOLOv6、YOLOv7…...
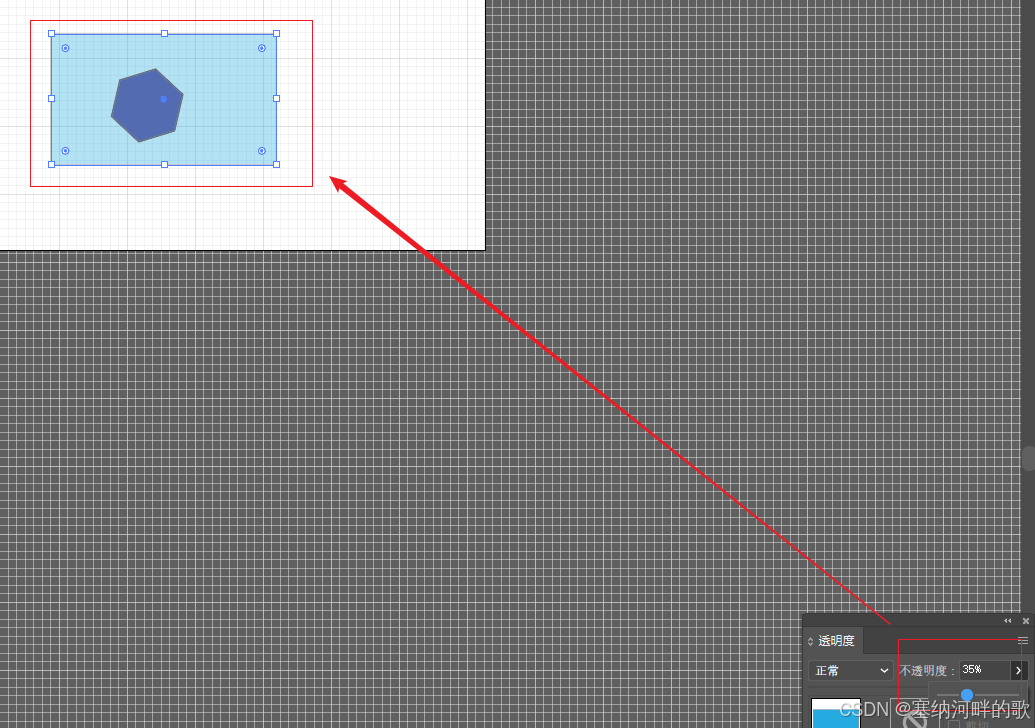
保姆级教程 | Adobe Illustrator调整颜色透明度
背景 由于课题需要,现需要在Adobe Illustrator里修改部分色块的颜色及透明度 步骤 1. 打开Adobe Illustrator软件,打开或创建一个AI文件: 2. 绘制一个色块: 3. 单击需要调整透明度的对象将其选中 4. 调整颜色的透明度…...

深入解读DeepSort目标跟踪算法:从状态预测到运动模型
在目标跟踪领域中,DeepSort(Deep Simple Online and Realtime Tracking)是一种广泛应用且高效的跟踪算法,它结合了深度学习与经典目标跟踪方法,为视觉跟踪任务提供了强大的解决方案。本文将深入探讨DeepSort中的关键概…...

24-10-2-读书笔记(二十二)-《契诃夫文集》(一)上([俄] 契诃夫 [译] 汝龙)啊!真想生活。
文章目录 《契诃夫文集》(一)上([俄] 契诃夫 [译] 汝龙 )早期生活——塔甘罗格(人物家庭简介)学生时期——莫斯科(写作与学习)流浪时期——哈萨林(游历与流浪)…...

【2024】前端学习笔记14-JavaScript常用数据类型-变量常量
学习笔记 1.JavaScript常用数据类型1.1.Number(数字)1.2.String(字符串)1.3.Boolean(布尔值)1.4.Null(空值)1.5.Undefined(未定义)1.6.Object(对象…...

Leecode热题100-48.旋转图像
给定一个 n n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。 你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。 示例 1: 输入:matrix [[1,2,3],[4,5,6],[7,8,9]] 输出…...
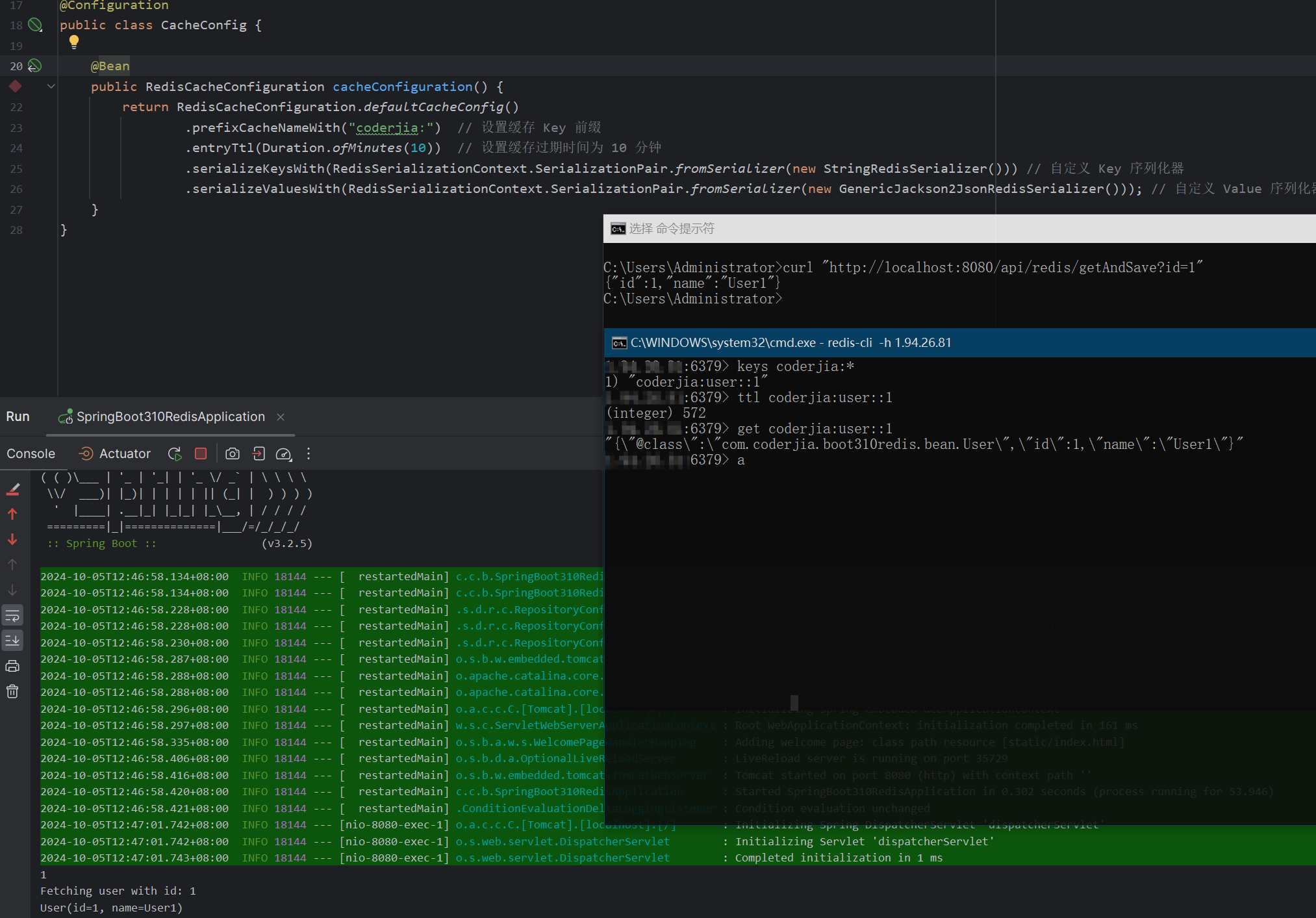
重学SpringBoot3-集成Redis(二)之注解驱动
更多SpringBoot3内容请关注我的专栏:《SpringBoot3》 期待您的点赞👍收藏⭐评论✍ 重学SpringBoot3-集成Redis(二)之注解驱动 1. 为什么选择 Redis 作为缓存?2. 如何在 Spring Boot 中启用 Redis 缓存?2.1 …...

【React】入门Day04 —— 项目搭建及登录与表单校验、token 管理、路由鉴权实现
项目搭建 创建项目 # 使用npx创建项目 npx create-react-app my-react-app # 进入项目目录 cd my-react-app # 创建项目目录结构 mkdir -p src/{apis,assets,components,pages,store,utils} touch src/{App.js,index.css,index.js} 使用npx create-react-app创建项目࿰…...

CMake 属性之目录属性
【写在前面】 CMake 的目录属性是指在特定目录(及其子目录)范围内有效的设置。 这些属性不同于全局变量或目标(Target)属性,它们提供了一种机制,允许开发者为项目中的不同部分定义不同的构建行为。 通过目录…...

ChatGPT:引领人工智能新潮流!
一、ChatGPT 是什么? 1. ChatGPT 的强大功能和广泛应用。 ChatGPT 作为一款先进的 AI 语言模型,拥有众多强大功能。它可以进行文本生成、文本分类、情感分析、机器翻译等多种自然语言处理任务。同时,ChatGPT 还能进行对话式交互,…...

【银河麒麟高级服务器操作系统】安全配置基线相关分析全过程及解决方案
了解更多银河麒麟操作系统全新产品,请点击访问 麒麟软件产品专区:https://product.kylinos.cn 开发者专区:https://developer.kylinos.cn 文档中心:https://documentkylinos.cn 服务器环境以及配置 【机型】物理机或虚机 【…...

用Python实现图片转ASCII艺术:图像处理与字符艺术的完美结合
解锁Python编程的无限可能:《奇妙的Python》带你漫游代码世界 ASCII艺术是一种通过字符来表现图像的艺术形式,最早用于早期计算机显示器,它仅支持字符显示。如今,尽管图像分辨率和显示技术得到了极大的提升,ASCII艺术作为一种复古而别具一格的图像表现形式,仍然受到许多…...

大数据-162 Apache Kylin 全量增量Cube的构建 Segment 超详细记录 多图
点一下关注吧!!!非常感谢!!持续更新!!! 目前已经更新到了: Hadoop(已更完)HDFS(已更完)MapReduce(已更完&am…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...
