k8s的安装和部署
配置三台主机,分别禁用各个主机上的swap,并配置解析
systemctl mask swap.target
swapoff -a
vim /etc/fstab

配置这三个主机上的主机以及harbor仓库的主机
所有主机设置docker的资源管理模式为system
[root@k8s-master ~]# vim /etc/docker/daemon.json
{
"registry-mirrors": ["https://reg.timinglee.org"],
"exec-opts": ["native.cgroupdriver=systemd"],
"log-driver": "json-file",
"log-opts": {
"max-size": "100m"
},
"storage-driver": "overlay2"
}将harbor仓库的证书保存
scp /etc/docker/certs.d/reg.timinglee.org/ca.crt root@192.168.38.100:/etc/docker/certs.d/reg.timinglee.org/ca.crt
启动docker,查看docker信息
systemctl enable --now docker
docker info安装K8s部署工具
添加k8s仓库,下载kubelet需要的版本以及他的插件
dnf install kubelet-1.30.0 kubeadm-1.30.0 kubectl-1.30.0 -y设置kubectl的命令补齐功能
dnf install bash-completion -y
echo "source <(kubectl completion bash)" >> ~/.bashrc
source ~/.bashrc在master主机上安装 cri-docker使用dockershim
dnf install libcgroup-0.41-19.el8.x86_64.rpm \
> cri-dockerd-0.3.14-3.el8.x86_64.rpm -y配置cri-docker的配置文件
vim /lib/systemd/system/cri-docker.service[Service]
Type=notify
ExecStart=/usr/bin/cri-dockerd --container-runtime-endpoint fd:// --networkplugin=cni --pod-infra-container-image=reg.timinglee.org/k8s/pause:3.9 #指定网络插件和基础容器镜像
ExecReload=/bin/kill -s HUP $MAINPID
TimeoutSec=0 #超时时间
RestartSec=2 重启时间2s
Restart=always #设置总是重启在master节点拉取k8s需要的镜像,将镜像上传到harbor仓库
#给镜像打上标签
docker images | awk '/google/{ print $1":"$2}' | awk -F "/" '{system("docker tag "$0" reg.timinglee.org/k8s/"$3)}'
#上传镜像
docker images | awk '/k8s/{system("docker push "$1":"$2)}'启动kubelet并进行初始化
systemctl status kubelet.servicekubeadm init --pod-network-cidr=10.244.0.0/16 \
--image-repository reg.timinglee.org/k8s \
--kubernetes-version v1.30.0 \
--cri-socket=unix:///var/run/cri-dockerd.sock指定集群配置文件的额变量
echo "export KUBECONFIG=/etc/kubernetes/admin.conf" >> ~/.bash_profile查看当前节点
kubectl get node由于当前没有安装 网络插件,所以当前没有容器没有运行
安装flannel
下载flannel镜像,并将其上传到haror仓库
#下载镜像,打标签
docker tag flannel/flannel:v0.25.5 \
reg.timinglee.org/flannel/flannel:v0.25.5
#上传到仓库
docker push reg.timinglee.org/flannel/flannel:v0.25.5
#相同操作
docker tag flannel/flannel-cni-plugin:v1.5.1-flannel1 \
reg.timinglee.org/flannel/flannel-cni-plugin:v1.5.1-flannel1
docker push reg.timinglee.org/flannel/flannel-cniplugin:v1.5.1-flannel1修改镜像下载位置
vim kube-flannel.ymlimage: reg.timinglee.org/flannel/flannel:v0.25.5
image: reg.timinglee.org/flannel/flannel-cni-plugin:v1.5.1-flannel1
image: reg.timinglee.org/flannel/flannel:v0.25.5安装
kubectl apply -f kube-flannel.yml加入集群
kubeadm token create --print-join-command查看节点状态
kubectl get nodes相关文章:

k8s的安装和部署
配置三台主机,分别禁用各个主机上的swap,并配置解析 systemctl mask swap.target swapoff -a vim /etc/fstab配置这三个主机上的主机以及harbor仓库的主机 所有主机设置docker的资源管理模式为system [rootk8s-master ~]# vim /etc/docker/daemon.json…...

第十八篇:一文说清楚ICMP的底层原理
作为程序员或者网络工程师,有时候无法访问对方主机;导致这个现象的有很多原因,那要排查具体的网络原因,可能会用到ping的指令。而ping的底层实现是互联⽹控制报⽂协议(ICMP)。 ICMP 全称是 Internet Contr…...

【优选算法】(第三十二篇)
目录 ⼆进制求和(easy) 题目解析 讲解算法原理 编写代码 字符串相乘(medium) 题目解析 讲解算法原理 编写代码 ⼆进制求和(easy) 题目解析 1.题目链接:. - 力扣(LeetCode&a…...
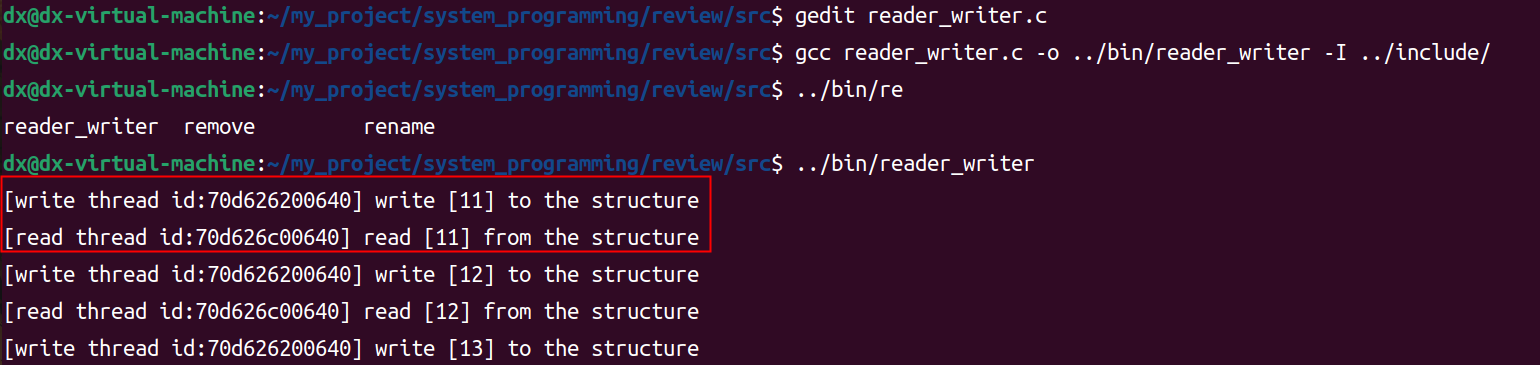
线程(四)线程的同步——条件变量
文章目录 线程线程的同步和互斥线程同步--条件变量什么是线程同步示例--条件变量的使用示例--使用两个线程对同一个文件进行读写示例--一个读者一个写者使用条件变量来实现同步 线程 线程的同步和互斥 线程同步–条件变量 是一个宏观概念,在微观上包含线程的相互…...
(上(这只是简单讲解)))
二维数组的旋转与翻转(C++)(上(这只是简单讲解))
二维数组的旋转与翻转(C) 引言 在计算机科学中,二维数组是一种常见的数据结构,广泛应用于图像处理、数据挖掘、机器学习等多个领域。二维数组的旋转与翻转是处理二维数据时经常需要用到的操作。本文将详细介绍二维数组的旋转与翻…...

【在Linux世界中追寻伟大的One Piece】System V共享内存
目录 1 -> System V共享内存 1.1 -> 共享内存数据结构 1.2 -> 共享内存函数 1.2.1 -> shmget函数 1.2.2 -> shmot函数 1.2.3 -> shmdt函数 1.2.4 -> shmctl函数 1.3 -> 实例代码 2 -> System V消息队列 3 -> System V信号量 1 -> Sy…...

【大数据】Spark弹性分布式数据集RDD详细说明
文章目录 整体介绍一、定义与特性二、操作与转换三、存储级别与持久化四、依赖关系与容错机制五、优化与性能调优 常见操作支持的数据格式1.文本文件 (Text Files)2. CSV 文件3. JSON 文件4. Parquet 文件5. Sequence Files6.Hadoop文件读取A. 读取HDFS上的文本文件B. 使用Hado…...

人参玉桂膏简介
一、产品基本信息 产品名称:人参玉桂膏 产品类别:植物饮料(专为特定体质设计) 配料:精选薏苡仁、荷叶、玉米须、赤小豆等纯然植物成分,辅以麦芽糖醇液、低聚果糖调节口感,陈皮、肉桂、人参&…...

消费者Rebalance机制
优质博文:IT-BLOG-CN 一、消费者Rebalance机制 在Apache Kafka中,消费者组 Consumer Group会在以下几种情况下发生重新平衡Rebalance: 【1】消费者加入或离开消费者组: 当一个新的消费者加入消费者组或一个现有的消费者离开消费…...

消息队列介绍
一、ActiveMQ 优点:性能单台(6000)成熟,已经在很多公司得到应用。各种协议支持好,有多个语言的成熟客户端 缺点:性能较弱,缺乏大规模吞吐的场景的应用,有江河日下之感 二、RabbitMQ…...

告别@Value,Spring Boot 3.3更优雅的配置注入方案
在Spring Boot的早期版本中,我们常使用Value注解来注入配置文件中的属性值。然而,这种方式虽然简单直接,却存在一些局限,比如它只能注入基本类型的值,并且需要显式地在每个需要注入的字段上使用注解。随着Spring Boot的…...

甲虫身体图像分割系统源码&数据集分享
甲虫身体图像分割系统源码&数据集分享 [yolov8-seg-EfficientRepBiPAN&yolov8-seg-C2f-FocusedLinearAttention等50全套改进创新点发刊_一键训练教程_Web前端展示] 1.研究背景与意义 项目参考ILSVRC ImageNet Large Scale Visual Recognition Challen…...

Qt - QMenu
QMenu 1、menu转string输出 //GlobalEnum.h #include <QObject> #include <QMetaEnum> class GlobalEnum : public QObject {Q_OBJECT public:EnumTest();enum Enum_Test{ZhangSan 0,WangWu,};Q_ENUM(Enum_Test) };#define EnumToString(e) \ QMetaEnum::fromTy…...

舵机驱动详解(模拟/数字 STM32)
目录 一、介绍 二、模块原理 1.舵机驱动原理 2.引脚描述 三、程序设计 main.c文件 servo.h文件 servo.c文件 四、实验效果 五、资料获取 项目分享 一、介绍 舵机(Servo)是在程序的控制下,在一定范围内连续改变输出轴角度并保持的电机系统。即舵机只支持…...

dvwa:文件包含、文件上传
文件包含 本地文件包含(敏感信息泄露)和远程文件包含(命令执行) 本地文件包含一般包含一些本地的敏感文件,如:/etc/passwd或/etc/shadow等 远程文件包含能使得服务器代码执行,如包含黑客vps的…...
——实现Windows服务内嵌WCF服务)
基于 C# .NET Framework 4.0 开发实现 WCF 服务实例详解(二)——实现Windows服务内嵌WCF服务
目录 引言 1. 创建一个新的Windows服务项目 2. 添加WCF服务 2.1 添加服务接口和实现 2.2 添加服务配置 3. 实现Windows服务 3.1 修改Service1类 3.2 在项目中添加ServiceInstaller 4. 安装和运行Windows服务 4.1 编译项目 4.2 使用InstallUtil.exe安装服务 …...

【ArcGIS/C#】调用控制台处理代码
代码示例 private static string[] run_conda_process(string command, Action<string> on_msg, CancellationTokenSource cancel){if (string.IsNullOrEmpty(command)){return new string[]{null,ArcGIS.Desktop.Internal.Core.Conda.Resources.Error_Unexpected + &qu…...

06_23 种设计模式之《适配器模式》
文章目录 一、适配器模式基础知识实例 一、适配器模式基础知识 适配器模式定义:将一个类的接口转换成客户希望的另一个接 口。适配器模式使得原本由于接口不兼容而不能一起工作的那些类可 以一起工作。 Client:客户端,调用自已需要的领域接口…...

Go语言--快速入门
Go语言特点 我们先看一下简单的Go语言程序 package mainimport "fmt"func main() { // 错误,{ 不能在单独的行上fmt.Println("Hello, World!") }我们可以看到外型非常像我们的JAVA,但是不需要;作为结尾,…...
京东云主机怎么用?使用京东云服务器建网站(图文教程)
京东云主机怎么用?非常简单,本文京东云服务器网jdyfwq.com使用以使用京东云服务器搭建WordPress博客网站为例,来详细说下京东云主机的使用方法。使用京东云服务器快速搭建WordPress网站教程,3分钟基于应用镜像一键搞定,…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

Vue3中的computer和watch
computed的写法 在页面中 <div>{{ calcNumber }}</div>script中 写法1 常用 import { computed, ref } from vue; let price ref(100);const priceAdd () > { //函数方法 price 1price.value ; }//计算属性 let calcNumber computed(() > {return ${p…...

针对药品仓库的效期管理问题,如何利用WMS系统“破局”
案例: 某医药分销企业,主要经营各类药品的批发与零售。由于药品的特殊性,效期管理至关重要,但该企业一直面临效期问题的困扰。在未使用WMS系统之前,其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...

【阅读笔记】MemOS: 大语言模型内存增强生成操作系统
核心速览 研究背景 研究问题:这篇文章要解决的问题是当前大型语言模型(LLMs)在处理内存方面的局限性。LLMs虽然在语言感知和生成方面表现出色,但缺乏统一的、结构化的内存架构。现有的方法如检索增强生成(RA…...

Pandas 可视化集成:数据科学家的高效绘图指南
为什么选择 Pandas 进行数据可视化? 在数据科学和分析领域,可视化是理解数据、发现模式和传达见解的关键步骤。Python 生态系统提供了多种可视化工具,如 Matplotlib、Seaborn、Plotly 等,但 Pandas 内置的可视化功能因其与数据结…...
