【超级详细解释】力扣每日一题 134.加油站 48. 旋转图像
134.加油站 力扣

这是一个很好的问题。这个思路其实基于一种贪心策略。我们从整个路径的油量变化来理解它,结合一个直观的“最低点法则”,来确保找到正确的起点。
问题的核心:油量差值的累积
对于每个加油站,我们有两个数组:gas(加油站提供的油量)和 cost(从当前加油站到下一个加油站所需的油量)。我们需要找到一个起点,使得可以绕行一圈回到该加油站,途中油量永远不为负数。
直观理解:寻找最低油量的原因
-
油量累积的曲线:
假设我们从某个加油站开始遍历整个环状加油站,每次计算当前的剩余油量累积,记为s(当前剩余油量)。每当我们经过一个加油站,我们就根据gas[i] - cost[i]来更新s,代表当前加油站加上油之后,减去到达下一个加油站的消耗。 -
最低点的特殊性:
在整个环中,油量累积s可能会上升或下降。如果我们画一条累积油量的曲线,从某个加油站出发计算到达其他加油站的油量变化,这条曲线中可能会有一些高点和低点。- 关键在于最低点:最低点代表了整个旅程中油量最匮乏的时刻。如果我们从其他加油站出发而不是这个最低点,意味着在到达最低点之前,我们已经有了更多的油量消耗,可能会在到达最低点之前出现负油量。因此,我们想要绕一圈成功的唯一可能,是从最低点之后开始,这样可以“错开”油量最紧张的时刻。
-
贪心选择最低点作为起点:
如果从最低点之后的某个加油站i + 1作为起点开始,意味着我们会在最低油量的地方重新开始计算油量变化,这样就可以确保从那时起油量逐步上升。换句话说,从最低点开始意味着我们从油量的最低点出发,此时“亏欠”的油量已经到达最低,我们后续不可能再遇到更差的情况,因此可以放心地从这里开始。
举例帮助理解
假设我们有以下油量情况:
gas = [1, 2, 3, 4, 5]cost = [3, 4, 5, 1, 2]
计算每个加油站的 gas[i] - cost[i] 的累积和:
- 第一个加油站开始:
s = 1 - 3 = -2 - 第二个加油站:
s = -2 + 2 - 4 = -4 - 第三个加油站:
s = -4 + 3 - 5 = -6 - 第四个加油站:
s = -6 + 4 - 1 = -3 - 第五个加油站:
s = -3 + 5 - 2 = 0
最低点是 -6,发生在第三个加油站之后,因此从第四个加油站(即 i + 1)作为起点开始,油量累积会逐步增加,最终可以保证绕一圈回到起点。
结论
在代码中,min_s 记录了油量的最低点,而 ans 则记录了从最低点之后开始的加油站。这样贪心地选择最低油量的下一个加油站作为起点,保证了我们可以绕完整个环。
从最低油量点的下一个加油站出发,可以让我们避免在已经处于最差的油量状态时出发,从而确保可以顺利走完一整圈。
```python
class Solution:def canCompleteCircuit(self, gas: List[int], cost: List[int]) -> int:n,m,index=len(gas),0,0if sum(gas)<sum(cost):return -1for i in range(n):m+=gas[i]-cost[i]if m<0:index=i+1m=0return index## 48.旋转图像
class Solution:
def rotate(self, matrix: List[List[int]]) -> None:
“”"
Do not return anything, modify matrix in-place instead.
“”"
n=len(matrix[0])
for i in range(n//2):
for j in range((n+1)//2):
tmp=matrix[i][j]
matrix[i][j]=matrix[n-1-j][i]
matrix[n-1-j][i]=matrix[n-1-i][n-1-j]
matrix[n-1-i][n-1-j]=matrix[j][n-1-i]
matrix[j][n-1-i]=tmp
class Solution:
def rotate(self, matrix: List[List[int]]) -> None:
n = len(matrix)
# 深拷贝 matrix -> tmp
tmp = copy.deepcopy(matrix)
# 根据元素旋转公式,遍历修改原矩阵 matrix 的各元素
for i in range(n):
for j in range(n):
matrix[j][n - 1 - i] = tmp[i][j]
作者:Krahets
链接:https://leetcode.cn/problems/rotate-image/solutions/1228078/48-xuan-zhuan-tu-xiang-fu-zhu-ju-zhen-yu-jobi/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
https://leetcode.cn/problems/rotate-image/solutions/1228078/48-xuan-zhuan-tu-xiang-fu-zhu-ju-zhen-yu-jobi
相关文章:

【超级详细解释】力扣每日一题 134.加油站 48. 旋转图像
134.加油站 力扣 这是一个很好的问题。这个思路其实基于一种贪心策略。我们从整个路径的油量变化来理解它,结合一个直观的“最低点法则”,来确保找到正确的起点。 问题的核心:油量差值的累积 对于每个加油站,我们有两个数组&…...

数据挖掘基本架构知识点
数据挖掘的基本架构主要包含以下几个部分: 一、数据获取 1. 数据源 - 可以是数据库(如关系型数据库MySQL、Oracle等)、文件系统(如CSV文件、XML文件等)、网络数据(如网页内容、社交媒体数据)等…...

LangChain中使用Prompt01
1.引入提示模板 from langchain.prompts import (SystemMessagePromptTemplate,AIMessagePromptTemplate,HumanMessagePromptTemplate, )2.设置系统提示 system_template_text"你是一位专业的翻译,能够将{input_language}翻译成{output_language},…...
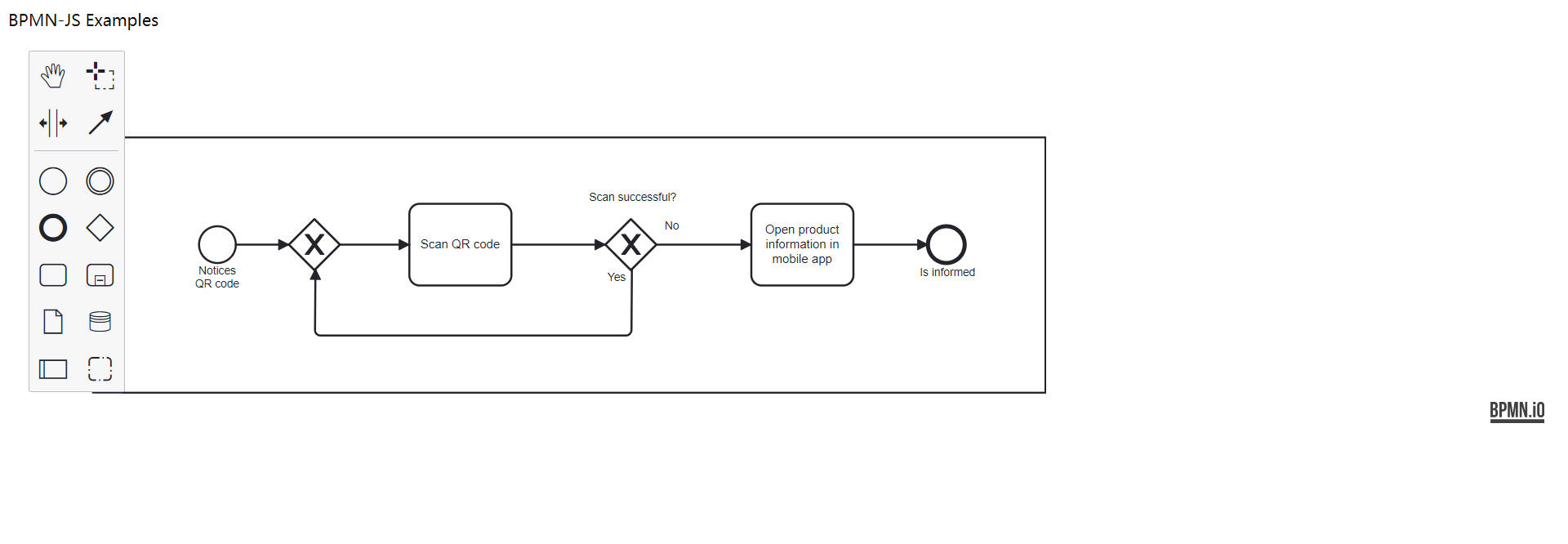
如何使用bpmn-js实现可视化流程管理
介绍 BPMN-JS是一个流行的开源库,用于在Web应用程序中可视化、创建、编辑和分析BPMN(Business Process Model and Notation,业务流程建模与表示法)2.0 图。BPMN是一种国际标准的图形化语言,用于描述企业中的业务流程&a…...

【PostgreSQL 】实战篇——如何使用 EXPLAIN 和 ANALYZE 工具分析查询计划和性能,优化查询
在数据库管理中,优化查询性能是确保应用程序高效运行的关键因素之一。 随着数据量的不断增长和复杂查询的增多,理解查询的执行计划变得尤为重要。 PostgreSQL 提供了强大的工具 EXPLAIN 和 ANALYZE,帮助开发者分析查询计划和性能࿰…...

List、Map、Set 三个接口存取元素时,各有什么特点
List、Map、Set是Java集合框架中的三个核心接口,它们在存取元素时各自具有独特的特点。以下是对这三个接口存取元素特点的详细分析: List接口 有序性: List中的元素是有序的,它们按照插入的顺序进行排列。 可重复性:…...

掌握 ASP.NET Web 开发:从基础到身份验证
ASP.NET 是微软开发的一个功能强大的框架,广泛用于构建现代化的 Web 应用程序。它支持 MVC 架构、Web API、Razor 语法,并提供完善的身份验证与授权机制。本文将介绍 ASP.NET 的基础知识、MVC 模式、Web API 开发、Razor 语法,以及如何实现身…...

【C++图文并茂】01背包问题不会?超详细的详解,看完保证你会
大家好,今天 给大家讲解01背包问题 有N件物品和一个容量为V的背包。第i件物品的体积是c[i],价值是w[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。 01背包问题是典型的动态规划问题,我们拿葡萄矿泉水和西…...

SQL自学:什么是子查询,如何使用它们
在 SQL(Structured Query Language,结构化查询语言)的世界里,子查询是一种强大的工具,它允许我们在一个 SQL 查询内部嵌套另一个查询。子查询也被称为内部查询或嵌套查询,为我们提供了一种灵活且强大的方式…...

No.10 笔记 | PHP学习指南:PHP数组掌握
本指南为PHP开发者提供了一个全面而简洁的数组学习路径。从数组的基本概念到高级操作技巧,我们深入浅出地解析了PHP数组的方方面面。无论您是初学者还是寻求提升的中级开发者,这份指南都能帮助您更好地理解和运用PHP数组,提高编码效率和代码质…...

RS-232 串口通信和 RS-485 串口通信的区别
RS-232 串口通信和 RS-485 串口通信有以下区别: 1. 通信方式: RS-232:全双工通信方式,即数据的发送和接收可以同时进行。在全双工模式下,通信双方可以在同一时刻既发送数据又接收数据,就像两个人可以同时…...
:Kubernetes 安全机制之 RBAC)
【K8s】专题十四(1):Kubernetes 安全机制之 RBAC
本文内容均来自个人笔记并重新梳理,如有错误欢迎指正! 如果对您有帮助,烦请点赞、关注、转发、订阅专栏! 专栏订阅入口 | 精选文章 | Kubernetes | Docker | Linux | 羊毛资源 | 工具推荐 | 往期精彩文章 【Docker】(全网首发)Kylin V10 下 MySQL 容器内存占用异常的解决…...

8. 多态、匿名内部类、权限修饰符、Object类
文章目录 一、多态 -- 花木兰替父从军1. 情境2. 小结 二、匿名内部类三、权限修饰符四、Object -- 所有类的父类(包括我们自己定义的类)五、内容出处 一、多态 – 花木兰替父从军 1. 情境 我们现在新建两个类HuaMuLan和HuaHu。HuMuLan是HuaHu的女儿,所以她会有她父…...
库(含示例代码))
CentOS/Ubuntu/Debian安装LibeventCentOS安装Libevent库(含示例代码)库(含示例代码)
使用命令:CentOS安装Libevent库(含示例代码) sudo yum install libevent-devel Ubuntu/Debian: sudo apt install libevent-dev 示例代码: #include <stdio.h> #include <stdlib.h> #include <unistd.h> …...

【大数据】数据采集工具sqoop介绍
文章目录 什么是sqoop?一、Sqoop的起源与发展二、Sqoop的主要功能三、Sqoop的工作原理四、Sqoop的使用场景五、Sqoop的优势六、Sqoop的安装与配置 sqoop命令行一、Sqoop简介与架构二、Sqoop特点三、Sqoop常用命令及参数四、使用示例五、注意事项 什么是sqoop? Sqoop是一款开…...
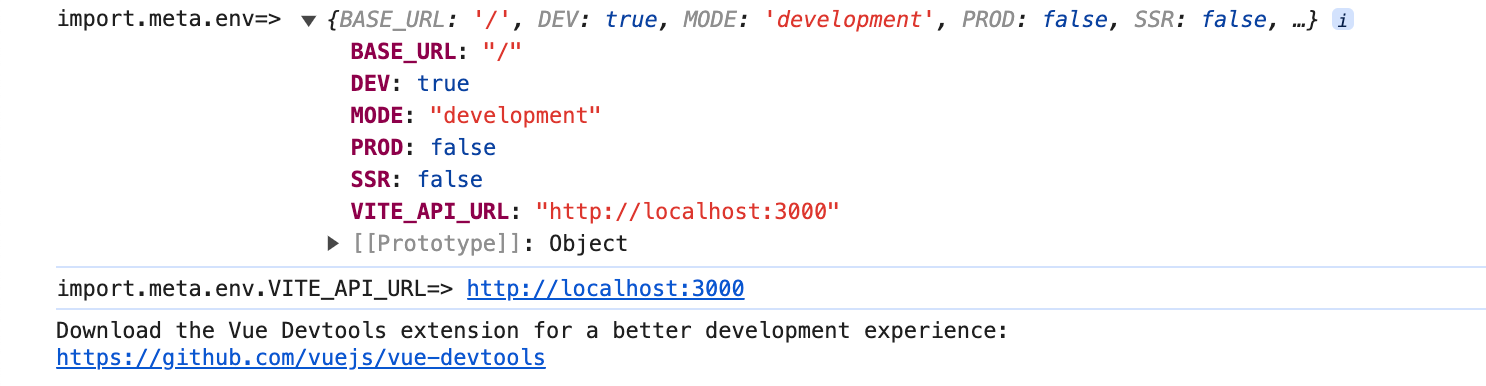
vite学习教程02、vite+vue2配置环境变量
文章目录 前言1、安装依赖2、配置环境变量3、应用环境变量4、运行和构建项目资料获取 前言 博主介绍:✌目前全网粉丝3W,csdn博客专家、Java领域优质创作者,博客之星、阿里云平台优质作者、专注于Java后端技术领域。 涵盖技术内容࿱…...

k8s 的网络通信
目录 1 k8s通信整体架构 2 flannel 网络插件 2.1 flannel 插件组成 2.2 flannel 插件的通信过程 2.3 flannel 支持的后端模式 3 calico 网络插件 3.1 calico 简介 3.2 calico 网络架构 3.3 部署 calico 1 k8s通信整体架构 k8s通过CNI接口接入其他插件来实现网络通讯。目前比较…...

【编程基础知识】掌握Spring MVC:从入门到精通
摘要: 本文将深入探讨Spring MVC框架的核心概念、组件和工作流程。读者将学习如何将Spring MVC应用于现代Web应用程序开发中,并通过实际代码示例和流程图,理解其强大的功能和灵活性。文章最后,我们将通过一个Excel表格总结全文内容…...

多线程下,@Transactional失效解决
一、问题复现 批量插入时,使用多线程对插入数据实现分批插入,在service层使用Transactional注解,对应方法中线程池中开辟的子线程抛出异常时,没有回滚事务。 二、原因分析 事务管理范围不正确:Transactional注解仅对…...

PyCharm 项目解释器切换指南:如何在项目中更换 Python Interpreter
PyCharm 项目解释器切换指南:如何在项目中更换 Python Interpreter 文章目录 PyCharm 项目解释器切换指南:如何在项目中更换 Python Interpreter一 Settings 设置二 Project 选项三 Conda Environment四 更换 Environment 本文详细介绍了在 macOS 系统中…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...

前端开发者常用网站
Can I use网站:一个查询网页技术兼容性的网站 一个查询网页技术兼容性的网站Can I use:Can I use... Support tables for HTML5, CSS3, etc (查询浏览器对HTML5的支持情况) 权威网站:MDN JavaScript权威网站:JavaScript | MDN...
