每日学习一个数据结构-图
文章目录
- 图基础
- 一、图的定义
- 二、图的相关概念
- 三、图的分类
- 四、图的使用场景
- 和图相关的算法
- 一、图的遍历算法
- 二、最短路径算法
- 三、最小生成树算法
- 四、图匹配算法
- 五、网络流算法
图基础
一、图的定义
在数学中,图是描述于一组对象的结构,其中某些对象对在某种意义上是“相关的”。这些对象对应于称为顶点的数学抽象(也称为节点或点),并且每个相关的顶点对都称为边(也称为链接或线)。通常,图形以图解形式描绘为顶点的一组点或环,并通过边的线或曲线连接。图(Graph)是由顶点的有穷非空集合和顶点之间的连线(边)的集合组成,通常表示为G=(V, E),其中G表示一个图,V(G)代表图G中的顶点集合,E(G)代表图G中的边集合。
二、图的相关概念
-
阶:图G中点集V的大小称作图G的阶。
-
子图:当图G’=(V’,E’),其中V’包含于V,E’包含于E,则G’称作图G=(V,E)的子图。每个图都是本身的子图。
-
生成子图:指满足条件V(G’)=V(G)的G的子图G’。
-
导出子图:
- 以图G的顶点集V的非空子集V1为顶点集,以两端点均在V1中的全体边为边集的G的子图,称为V1导出的导出子图。
- 以图G的边集E的非空子集E1为边集,以E1中边关联的顶点的全体为顶点集的G的子图,称为E1导出的导出子图。
-
度:一个顶点的度是指与该顶点相关联的边的条数,顶点v的度记作d(v)。
-
入度和出度:对于有向图来说,一个顶点的度可细分为入度和出度。一个顶点的入度是指与其关联的各边之中,以其为终点的边数;出度则是相对的概念,指以该顶点为起点的边数。
-
自环:若一条边的两个顶点为同一顶点,则此边称作自环。
-
路径:从u到v的一条路径是指一个序列v0,e1,v1,e2,v2,…ek,vk,其中ei的顶点为vi及vi-1,k称作路径的长度。如果它的起止顶点相同,该路径是“闭”的,反之,则称为“开”的。
-
简单路径:如果路径中除起始与终止顶点可以重合外,所有顶点两两不等,则称为简单路径。
-
行迹:如果路径P(u,v)中的边各不相同,则该路径称为u到v的一条行迹。
-
轨道:如果路径P(u,v)中的顶点各不相同,则该路径称为u到v的一条轨道。
-
回路和圈:闭的行迹称作回路(Circuit),闭的轨称作圈(Cycle)。
-
桥:若去掉一条边,便会使得整个图不连通,该边称为桥。
三、图的分类
-
无向图和有向图:
- 无向图:边没有方向的图。在无向图中,边记作(vi,vj),它蕴涵着存在< vi,vj>和< vj,vi>两条弧。若无向图中有n个顶点,则最多有n(n-1)/2条弧。
- 有向图:给图的每条边规定一个方向得到的图。在有向图中,边称作弧,含箭头的一端称为弧头,另一端称为弧尾。在有向图中,路径也是有向的。
-
简单图、多重图、完全图:
- 简单图:图中若不存在顶点到其自身的边,并且同一条边不会重复出现,这种图称为简单图。简单图分为简单无向图和简单有向图。
- 多重图:图中某两个顶点之间的边数多于一条,或者顶点通过一条边和自己关联,这种图称为多重图。多重图分为多重无向图和多重有向图。数据结构中所讨论的图一般都是简单图。
- 完全图:在无向图中,如果任意两个顶点之间都存在边,则称该图为无向完全图。含有n个顶点的无向完全图有n(n-1)/2条边。在有向图中,如果任意两个顶点之间都存在方向相反的两条弧,则称该图为有向完全图。含有n个顶点的有向完全图有n(n-1)条边。
-
稀疏图和稠密图:有
很少条边或者弧的图称为稀疏图,反之称为稠密图。稀疏和稠密都是相对而言的,并不是一个精确的数值。
四、图的使用场景
图是一种非常重要的数据结构,在多个领域都有广泛的应用:
- 计算机科学:图论被广泛应用于算法设计中,如最短路径算法、网络流算法等。此外,图还是许多数据结构的基础,如邻接表、邻接矩阵等。
- 工程领域:在电路设计中,图可以用来表示电路元件之间的连接关系;在机械设计中,图可以用来表示零件之间的装配关系。
- 社会学:在社会网络分析中,图可以用来表示人与人之间的社会关系,如朋友关系、合作关系等。
- 生物学:在生物信息学中,图可以用来表示基因之间的相互作用关系、蛋白质之间的相互作用关系等。
- 经济学和金融学:图可以用来表示不同经济实体之间的交易关系、投资关系等。
- 地理信息系统:在GIS中,图可以用来表示地理实体之间的空间关系,如城市之间的交通网络、河流的流向等。
总的来说,图作为一种强大的工具,在各个领域都发挥着重要的作用。通过构建和分析图,人们可以更好地理解和解决复杂的问题。
和图相关的算法
图是一种重要的数据结构,由顶点(或节点)和边组成,用于表示对象及其相互之间的关系。以下是与图相关的一些经典算法:
一、图的遍历算法
-
广度优先搜索(BFS)

- 从起始节点开始,先访问所有相邻的节点,再依次访问这些相邻节点的未访问过的相邻节点,直到所有节点都被访问过。
- 适用于寻找最短路径(未考虑边权)等问题。
- 实现时通常使用队列数据结构。
-
深度优先搜索(DFS)

- 从起始节点开始,沿着一个分支尽可能深地搜索,直到该分支的末端,然后回溯到上一个节点,继续搜索其他未访问的分支。
- 适用于解决连通性问题、路径查找、图的遍历等问题。
- 可以通过递归或显式栈来实现。
-
A*算法
- 启发式搜索算法,使用启发式函数来评估从源节点到目标节点的路径成本。
- 通过优先队列来选择下一个要访问的节点,以找到最短路径。
- 估值函数f(n)=g(n)+h(n),其中g(n)是从起始搜索点到当前点的代价,h(n)是当前结点到目标结点的估值。
二、最短路径算法
-
Dijkstra算法
- 解决单源最短路径问题,即求出给定顶点到其他任一顶点的最短路径。
- 适用于加权图,且图中不包含负权边。
- 算法依据最短路径的最优子结构性质,从起点开始,每一步都走最短的路径,并不断更新每个点到起点的最短距离。
-
Bellman-Ford算法
- 解决含负权图的单源最短路径问题。
- 通过连续进行松弛操作来更新最短路径估计值。
- 如果在n-1次松弛后还能更新,则说明图中有负环,因此无法得出结果。
-
Floyd-Warshall算法
- 解决任意两点间的最短路径问题。
- 适用于所有类型的图,包括有向图和带负权边的图。
- 算法通过考虑最佳子路径来得到最佳路径,使用邻接矩阵来储存边。
三、最小生成树算法
-
Prim算法
- 在加权连通图中搜索最小生成树。
- 从任意一个顶点开始,逐步扩展生成树,每次选择权值最小的连接新顶点和生成树中顶点的边。
-
Kruskal算法
- 另一种求加权连通图的最小生成树的算法。
- 基于贪心策略,首先将所有边按权值从小到大排序,然后依次选择边,如果选择的边不会形成环,则将其加入生成树中。
四、图匹配算法
-
匈牙利算法
- 在多项式时间内求解任务分配问题的组合优化算法。
- 用于求解指派问题(assignment problem),算法时间复杂度为O(n^3)。
- 适用于二分图的最大匹配问题。
五、网络流算法
-
Ford-Fulkerson算法
- 用于计算流网络中的最大流量。
- 流网络是一个有向图,其中每条边都有一个非负容量。
- 算法通过寻找增广路径来不断更新流量,直到无法再找到增广路径为止。
这些算法在图论和网络分析中有着广泛的应用,包括网络路由、社交媒体分析、推荐系统等领域。根据具体问题的需求和图的结构特性,可以选择合适的算法来解决问题。
相关文章:

每日学习一个数据结构-图
文章目录 图基础一、图的定义二、图的相关概念三、图的分类四、图的使用场景 和图相关的算法一、图的遍历算法二、最短路径算法三、最小生成树算法四、图匹配算法五、网络流算法 图基础 一、图的定义 在数学中,图是描述于一组对象的结构,其中某些对象对…...
kali(专业的渗透测试虚拟机)|kali下载链接地址 |kali安装 |kali部署指南
介绍 kali 是Debian开源linux系统体系下的子分支之一 Debian-kali 扩展:Ubuntu也是Debian开源linux系统体系下的子分支之一 Debian-ubuntu 安装kali 2023.03 稳定版 Index of /kali-images/kali-2023.1/ 安装可以参考他的教程, 写的很详细了…...

中国地级市生态韧性数据及城市生态韧性数据(2000-2022年)
一测算方式: 参考C刊《管理学刊》楚尔鸣(2023)老师的做法,城市生态韧性主要衡量一个城市在面临生态环境系统压力或突发冲击时,约束污染排放、维护生态环境状态和治理能力提升的综合水平。 参考郭海红和刘新民的研究&a…...

应对网络安全挑战:App等保测评的重要性与策略
在全球数字化转型的大潮中,移动应用(App)作为连接人们日常生活与互联网世界的桥梁,其数量与日俱增,功能日趋多样化。与此同时,App背后潜藏的网络安全风险也随之上升,数据泄露、隐私侵犯、恶意软件植入等问题频发&#…...

vue后台管理系统从0到1搭建(4)各组件的搭建
文章目录 vue后台管理系统从0到1搭建(4)各组件的搭建Main.vue 组件的初构 vue后台管理系统从0到1搭建(4)各组件的搭建 Main.vue 组件的初构 根据我们的效果来看,分析一下,我们把左边的区域分为一个组件&am…...
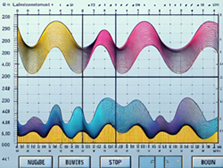
LabVIEW开关磁阻电机特性测量系统
基于LabVIEW软件和特定硬件组件的开关磁阻电机(SRM)特性测量系统,结合多功能数据采集卡,统能够准确地测量并分析SRM的电磁特性,从而支持电机模型的精确建立和性能优化。 项目背景 在工业生产和家用电器领域࿰…...

在当前网络环境中查看所有IPv4与Mac地址的方法
在powershell界面中: # 获取并显示所有网络接口的MAC地址和IPv4地址 Get-NetAdapter | Select-Object -Property Name, MacAddress, Status Get-NetAdapter | Get-NetIPAddress -AddressFamily IPv4 | Select-Object -Property InterfaceAlias, IPAddress, PrefixL…...

CSS @规则(At-rules)系列详解___@charset规则使用方法
CSS 规则(At-rules)系列详解 ___charset规则使用方法 本篇目录: 零、时光宝盒 一、charset规则定义和用法 二、CSS charset语法 三、charset 使用方法例子 1、正确使用方法 2、无效的,错误的使用方法 零、时光宝盒 (https://blog.csd…...
黑马程序员C++核心编程学习笔记
黑马程序员C核心编程学习笔记 一、内存 1.1 内存四区 C程序在执行时,将内存大致分为4个区域:代码区,全局区,栈区,堆区 代码区:存放函数体的的二进制代码,操作系统管理。 🔵特点&a…...

六自由度平台
力姆泰克六自由度平台 安装方便,维护简单 多重机械电气安全保护 向下翻动查看更多 力姆泰克伺服系统集成 全新革命性结构设计与六轴先进伺服控制原理的结合,力姆泰克公司引进国外的专业技术在国内全新推出 全电动六自由度平台。将完全替代市场上原有的…...

【Node.js 下载及npm安装配置】亲测可用
Node.js 下载及npm安装配置 安装nodejs设置安装angular 安装nodejs 下载适用自己系统的node.js,官网:https://nodejs.cn/download/。默认安装即可。查看是否安装成功,node -v,npm -v ,出现版本号即安装成功。 设置 …...

Qt C++设计模式->访问者模式
访问者模式(Visitor Pattern)是一种行为型设计模式,它将操作与对象结构分离,使得你可以在不改变对象结构的前提下定义作用于这些对象的新操作。访问者模式通过引入一个访问者对象,允许你在不修改类的前提下向已有类添加…...

手机在网状态的详细应用场景有哪些?
手机在网状态的详细应用场景涵盖了多个行业和领域,以下是一些具体的例子: 金融行业 风控审核:银行、贷款公司等金融机构在审批贷款或信用卡时,可以通过查询手机在网状态来验证申请人的手机号码是否真实有效,从而降低欺…...

Linux的kafka安装部署
1.kafka是一个分布式的,去中心化的,高吞吐低延迟,订阅模式的消息队列系统 确保要有jdk与zookeeper安装配置 2.下载kafka安装包 http://archive.apache.org/dist/kafka/2.4.1/kafka_2.12-2.4.1.tgz 此时可以wget http://archive.apache.org/dist/kafka/2.4.1/kafka_2.12-2.4.…...

docker部署虚拟机
创建新的容器web02,-v表示目录映射,-p时端口映射,把宿主机目录挂载到容器中 docker run -itd -p 80:80 -v /data/webapps/www/:/usr/share/nginx/html/ --nameweb02 nginx:latest 此时我们在发布网站时只需要放在宿主机的目录里就可以了 解…...
如何用ChatGPT 8小时写出一篇完整论文(附完整提示词)
今天教大家如何利用ChatGPT完成一篇完整的论文。只需要一个标题,剩下全部由ChatGPT完成。总耗时8小时。 阅前提醒: 1.适用人群:这个方法适合应付简单的学术任务,比如日常小论文或投稿一般期刊。但如果你要写高水平的论文…...

AWS MySQL 升级(三)—— TAZ - 近0停机的小版本升级方案
与AWS交流了解到的新方案,没有实际试过,所以本篇主要是些原理 一、 TAZ的含义 TAZ实际上就是 3 AZ,扩展一些就是 Multi-AZ DB Cluster,即在3个可用区部署DB,具备两个只读备用实例。 二、 TAZ的主要用途 1. 近0停机的小…...

Redis的应用以及Redis工具类的封装
在前后端分离的项目中,通过session和cookie的通信一般就失去效益了,即使这么做了也会产生著名的漏洞问题CSRF(Cross-site request forgery), 是一种挟制用户在当前已登录的Web应用程序上执行非本意的操作的攻击方法。因…...

E系列I/O模块在锂电装备制造系统的应用
为了满足电池生产线对稳定性和生产效率的严苛要求,ZLG致远电子推出高速I/O应用方案,它不仅稳定可靠,而且速度快,能够迅速响应生产需求。 锂电池的生产工艺较为复杂,大致分为三个主要阶段:极片制作、电芯制作…...

ElasticsearchClient入门指南
在本教程中,我们将探讨如何使用Elasticsearch的官方Java客户端 - ElasticsearchClient。这个强大的工具允许您的Java应用程序与Elasticsearch集群进行交互,执行各种操作,如索引文档、执行搜索查询等。 前提条件 在开始之前,确保您的项目中已经包含了必要的依赖。您可以通过Ma…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...
