【LeetCode】动态规划—309. 买卖股票的最佳时机含冷冻期(附完整Python/C++代码)
动态规划—309. 买卖股票的最佳时机含冷冻期
- 题目描述
- 前言
- 基本思路
- 1. 问题定义
- 2. 理解问题和递推关系
- 状态定义:
- 状态转移公式:
- 初始条件:
- 3. 解决方法
- 动态规划方法
- 伪代码:
- 4. 进一步优化
- 5. 小总结
- Python代码
- Python代码解释总结
- C++代码
- C++代码解释总结
- 总结
题目描述

前言
最佳买卖股票时机含冷冻期问题 是一个经典的动态规划问题。给定一个数组表示股票的价格,每天你只能做一件事:买入股票、卖出股票或者冷冻(休息)。如果你在一天卖出了股票,那么第二天你无法进行任何交易(有一天的冷冻期)。目标是通过买卖股票来获得最大的收益。该问题要求我们结合动态规划的思想,合理规划买卖操作,以获取最大的利润。
基本思路
1. 问题定义
给定一个数组 prices,其中 prices[i] 表示第 i 天的股票价格。你可以在任意天选择买入或卖出股票,但在卖出股票后的第二天不能买入(有一天冷冻期)。目标是找到能够获得的最大利润。
2. 理解问题和递推关系
为了帮助我们理解该问题的动态规划思路,我们可以定义几种状态来表示我们在某一天的持有情况。主要有以下三种状态:
状态定义:
-
持有股票的状态(
hold):hold[i]表示在第i天结束时,我们持有股票时的最大收益。- 这个状态可以从两种情况转移而来:要么是之前买入并继续持有(
hold[i-1]),要么是今天刚刚买入。
-
未持有股票且处于冷冻期的状态(
cooldown):cooldown[i]表示在第i天结束时,我们处于冷冻期时的最大收益(也就是说,第i天刚卖出股票,不能买入股票)。- 这个状态只能通过在
i天卖出股票后进入,因此cooldown[i] = hold[i-1] + prices[i]。
-
未持有股票且不处于冷冻期的状态(
sell):sell[i]表示在第i天结束时,我们没有持有股票且没有处于冷冻期的最大收益。- 这个状态有两种来源:要么是处于冷冻期后过了一天(
cooldown[i-1]),要么是之前一直不持有股票(sell[i-1])。
状态转移公式:
-
hold[i] = max(hold[i-1], sell[i-1] - prices[i])- 要么我们继续持有股票,要么我们在第
i天买入股票。
- 要么我们继续持有股票,要么我们在第
-
cooldown[i] = hold[i-1] + prices[i]- 表示我们在第
i天卖出了股票,进入冷冻期。
- 表示我们在第
-
sell[i] = max(sell[i-1], cooldown[i-1])- 表示我们处于不持有股票且不在冷冻期的状态,可以是冷冻期结束或者一直未持有股票。
初始条件:
hold[0] = -prices[0]:表示在第 0 天买入股票的收益。sell[0] = 0:在第 0 天不持有股票,收益为 0。cooldown[0] = 0:在第 0 天没有冷冻期,收益为 0。
3. 解决方法
动态规划方法
- 定义
hold[i],cooldown[i]和sell[i]来表示每一天的三种状态的最大收益。 - 使用递推公式更新这三种状态的值。
- 最终结果为
max(sell[n-1], cooldown[n-1]),即在最后一天没有持有股票时的最大收益。
伪代码:
initialize hold[0] = -prices[0], sell[0] = 0, cooldown[0] = 0
for each day i from 1 to n-1:hold[i] = max(hold[i-1], sell[i-1] - prices[i])cooldown[i] = hold[i-1] + prices[i]sell[i] = max(sell[i-1], cooldown[i-1])
return max(sell[n-1], cooldown[n-1])
4. 进一步优化
- 空间优化:由于
dp[i]仅依赖于dp[i-1],我们可以将动态规划中的hold、cooldown和sell状态用常量来代替,从而将空间复杂度优化到O(1)。
5. 小总结
- 问题思路:通过将状态分为持有股票、未持有且处于冷冻期、未持有且不在冷冻期三种情况,动态规划可以清晰地描述问题的状态转移过程。
- 时间复杂度:该算法的时间复杂度为
O(n),空间复杂度可以优化为O(1)。
以上就是买卖股票的最佳时机含冷冻期问题的基本思路。
Python代码
class Solution:def maxProfit(self, prices: list[int]) -> int:if not prices:return 0n = len(prices)# 初始化第0天的状态hold = -prices[0]sell = 0cooldown = 0for i in range(1, n):# 更新状态new_hold = max(hold, sell - prices[i])new_cooldown = hold + prices[i]new_sell = max(sell, cooldown)# 更新hold, cooldown, sellhold, cooldown, sell = new_hold, new_cooldown, new_sell# 返回sell和cooldown中的较大值return max(sell, cooldown)
Python代码解释总结
- 初始化:在第 0 天,如果持有股票,则收益为
-prices[0],否则为0。 - 状态转移:通过递推公式更新每一天的
hold、cooldown和sell状态。 - 返回结果:在最后一天,返回不持有股票状态下的最大收益,即
max(sell, cooldown)。
C++代码
#include <vector>
#include <algorithm>
using namespace std;class Solution {
public:int maxProfit(vector<int>& prices) {if (prices.empty()) return 0;int n = prices.size();// 初始化第0天的状态int hold = -prices[0];int sell = 0;int cooldown = 0;for (int i = 1; i < n; ++i) {// 更新状态int new_hold = max(hold, sell - prices[i]);int new_cooldown = hold + prices[i];int new_sell = max(sell, cooldown);// 更新hold, cooldown, sellhold = new_hold;cooldown = new_cooldown;sell = new_sell;}// 返回sell和cooldown中的较大值return max(sell, cooldown);}
};
C++代码解释总结
- 初始化:在第 0 天,如果持有股票,则收益为
-prices[0],否则为0。 - 状态转移:通过递推公式更新每一天的
hold、cooldown和sell状态。 - 返回结果:在最后一天,返回不持有股票状态下的最大收益,即
max(sell, cooldown)。
总结
- 核心思想:通过将买卖股票问题划分为持有股票、未持有且处于冷冻期、未持有且不在冷冻期三种状态,动态规划可以清晰地模拟问题的状态转移过程。
- 时间复杂度:该算法的时间复杂度为
O(n),可以处理大规模的输入。 - 空间优化:由于每个状态只依赖前一天的状态,空间复杂度可以从
O(n)优化为O(1)。
相关文章:

【LeetCode】动态规划—309. 买卖股票的最佳时机含冷冻期(附完整Python/C++代码)
动态规划—309. 买卖股票的最佳时机含冷冻期 题目描述前言基本思路1. 问题定义2. 理解问题和递推关系状态定义:状态转移公式:初始条件: 3. 解决方法动态规划方法伪代码: 4. 进一步优化5. 小总结 Python代码Python代码解释总结 C代…...
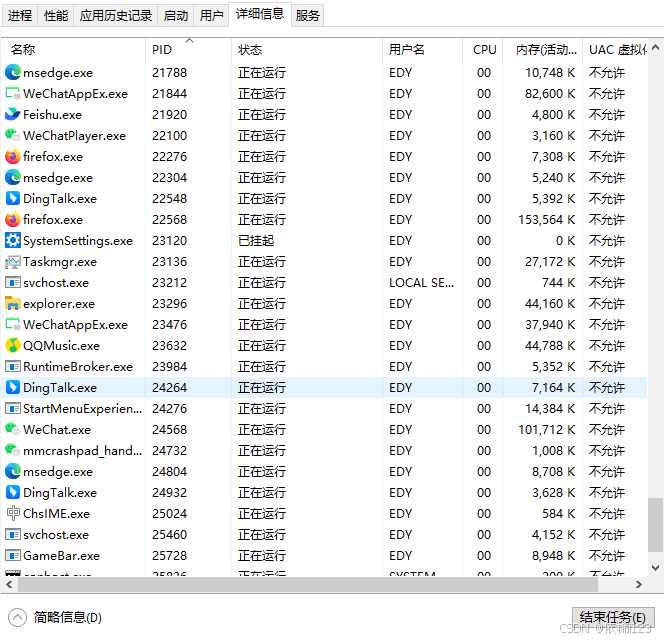
IDE启动失败
报错:Cannot connect to already running IDE instance. Exception: Process 24,264 is still running 翻译:无法连接到已运行的IDE实例。异常:进程24,264仍在运行 打开任务管理器,找到PID为24264的CPU线程,强行结束即可。 【Ct…...
【Kubernetes】常见面试题汇总(六十)
目录 131. pod 一直处于 pending 状态? 132. helm 安装组件失败? 特别说明: 题目 1-68 属于【Kubernetes】的常规概念题,即 “ 汇总(一)~(二十二)” 。 题目 69-113 属于…...

maven dependency中scope的取值类型
在 Maven 中,<scope> 标签用于定义依赖项的范围,以指定依赖在不同阶段的可见性和生命周期。以下是 Maven 中常见的 <scope> 取值类型的详细介绍: 1. **compile**: - 默认的依赖范围,适用于编译、测试和…...
线性代数在大一计算机课程中的重要性
线性代数在大一计算机课程中的重要性 线性代数是一门研究向量空间、矩阵运算和线性变换的数学学科,在计算机科学中有着广泛的应用。大一的计算机课程中,线性代数的学习为学生们掌握许多计算机领域的关键概念打下了坚实的基础。本文将介绍线性代数的基本…...

笔记本电脑按住电源键强行关机,对电脑有伤害吗?
电脑卡住了,我们习惯性地按住电源键或者直接拔掉电源强制关机,但这种做法真的安全吗?会不会对电脑造成伤害呢? 其实,按住电源键关机和直接拔掉电源关机是不一样的。它们在硬件层面有着本质区别。 按住电源键关机 当…...

如何将 cryptopp库移植到UE5内
cryptopp是一个开源免费的算法库,这个库的用途非常多,我常常用这个库来做加解密的运算。这段时间在折腾UE5.4.4,学习的过程中,准备把cryptopp移植到游戏的工程内,但UE的编译环境和VS的编译环境完全不同,能在…...

SpringBoot 集成GPT实战,超简单详细
Spring AI 介绍 在当前的AI应用开发中,像OpenAI这样的GPT服务提供商主要通过HTTP接口提供服务,这导致大部分Java开发者缺乏一种标准化的方式来接入这些强大的语言模型。Spring AI Alibaba应运而生,它作为Spring团队提供的一个解决方案&…...

基于Langchain框架下Prompt工程调教大模型(LLM)[输入输出接口、提示词模板与例子选择器的协同应用
大家好,我是微学AI,今天给大家介绍一下基于Langchain框架下Prompt工程调教大模型(LLM)[输入输出接口、提示词模板与例子选择器的协同应用。本文深入探讨了Langchain框架下的Prompt工程在调教LLM(大语言模型)方面的应用,…...

Vue基于vue-office实现docx、xlsx、pdf文件的在线预览
文章目录 1、vue-office概述2、效果3、实现3.1 安装3.2 使用示例3.2.1 docx文档的预览3.2.2 excel文档预览3.2.3 pdf文档预览1、vue-office概述 vue-office是一个支持多种文件(docx、.xlsx、pdf)预览的vue组件库,支持vue2和vue3。 功能特色: 一站式:提供docx、.xlsx、pdf多…...
哪个软件可以在线编辑ppt? 一口气推荐5个做ppt的得力助手!
日常在制作ppt时,你是否经常遇到这些问题,ppt做到一半,电脑突然死机,来不及保存的ppt付之一炬,分分钟让人原地崩溃…… 好在许多团队也在持续跟进这个问题,给出了一个一劳永逸的最佳方案——PPT在线编辑&a…...

Django学习笔记九:Django中间件Middleware
Django中间件(Middleware)是一段在Django的请求/响应处理过程中,可以介入并改变请求或响应的代码。中间件是Django框架中一个非常强大的功能,它允许你在Django的视图函数之前或之后执行自定义代码。 中间件可以用于: …...

原来自媒体高手都是这样选话题的,活该人家赚大钱,真后悔知道晚了
做自媒体,话题是战略,内容是战术。 战略是要做正确的事情,战术是如何正确地做事。 如果战略上错误,战术上再勤奋努力都无济于事。 《孙子兵法》有云:“胜者先胜而后求战,败者先战而后求胜。” 相信很多…...

胤娲科技:AI绘梦师——一键复刻梵高《星空》
想象一下,你手中握有一张梵高的《星空》原图,只需轻轻一点,AI便能化身绘画大师,一步步在画布上重现那璀璨星河。 这不是科幻电影中的桥段,而是华盛顿大学科研团队带来的“Inverse Painting”项目,正悄然改变…...

第18课-C++继承:探索面向对象编程的复用之道
一、引言 C 作为一种强大的编程语言,继承机制在面向对象编程中扮演着至关重要的角色。它允许开发者基于已有的类创建新的类,从而实现代码的复用和功能的扩展。然而,继承的概念和使用方法并非一目了然,特别是在处理复杂的继承关系时…...

麒麟V10系统下的调试工具(网络和串口调试助手)
麒麟V10系统下的调试工具(网络和串口调试助手) 1.安装网络调试助手mnetassist arm64-main ①在linux下新建一个文件夹 mkdir /home/${USER}/NetAssist②将mnetassist arm64-main.zip拷贝到上面文件夹中,并解压给权限 cd /home/${USER}/Ne…...

ssh封装上传下载
pip install paramiko import paramikoclass SSHClient:def __init__(self, host, port, username, password):self.host = hostself.port = portself.username = usernameself.password = passwordself.ssh = Noneself.sftp = Nonedef connect(self):"""连接到…...

018_FEA_Structure_Static_in_Matlab结构静力学分析
刹车变形分析 本示例展示了如何使用 MATLAB 软件进行刹车变形分析。 这个例子是Matlab官方PDE工具箱的第一个例子,所需要的数据文件都由Matlab提供,包括CAD模型文件。 步骤 1: 导入 CAD 模型 导入 CAD 模型,这里使用的是一个带有孔的支架模…...

网页打不开、找不到服务器IP地址
现象:网络连接ok,软件能正常使用,当网页打不开。 原因:DNS 配置错误导致网站域名无法正确解析造成。 影响DNS设置的:VPN软件、浏览器DNS服务选择、IPv4属性被修改。 1、VPN代理未关闭 2、浏览器DNS解析选择 3、以太…...
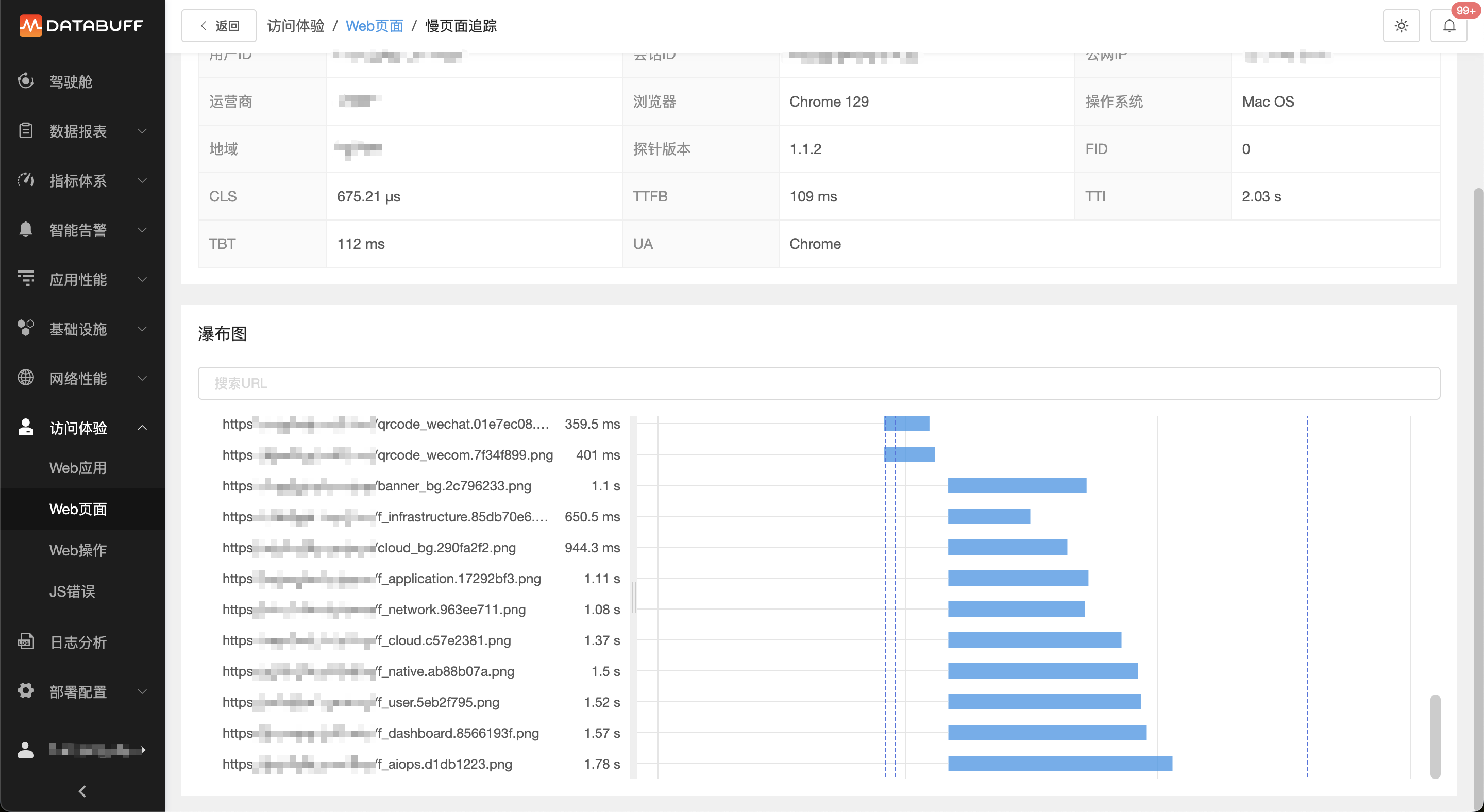
RUM性能优化之图片加载
作者:三石 在现代Web开发中,图片作为内容表达的核心元素,其加载效率直接影响到页面的整体性能和用户体验。随着高清大图和动态图像的普及,优化图片加载变得尤为重要。RUM作为一种主动监测技术,能够帮助开发者从真实用户…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...
