交叉熵损失函数(Cross-Entropy Loss Function)解释说明
公式 8-11 的内容如下:
L ( y , a ) = − [ y log a + ( 1 − y ) log ( 1 − a ) ] L(y, a) = -[y \log a + (1 - y) \log (1 - a)] L(y,a)=−[yloga+(1−y)log(1−a)]
这个公式表示的是交叉熵损失函数(Cross-Entropy Loss Function),它广泛用于二分类问题,尤其是神经网络的输出层为 sigmoid 激活函数的情况下。让我们详细解释这个公式的含义。
1. 公式的组成部分:
-
y y y:表示真实标签,它的值通常为 0 或 1。
- y = 1 y = 1 y=1 表示样本属于正类。
- y = 0 y = 0 y=0 表示样本属于负类。
-
a a a:表示模型的预测输出值。由于此处的激活函数为 Sigmoid 函数,所以输出 a a a 是一个概率值,范围为 0 ≤ a ≤ 1 0 \leq a \leq 1 0≤a≤1。可以理解为模型预测该样本属于正类的概率。
-
log a \log a loga 和 log ( 1 − a ) \log (1 - a) log(1−a):分别表示预测为正类和负类时的对数损失。
2. 交叉熵损失的解释:
交叉熵损失是用来衡量两个概率分布之间的差异。在这里,它衡量的是模型的预测概率分布 a a a 与真实分布 y y y 之间的差异。损失函数的形式通过对数函数来放大预测误差较大的情况,以此来惩罚错误的预测。
-
当 y = 1 y = 1 y=1 时:
L ( y , a ) = − log a L(y, a) = -\log a L(y,a)=−loga这意味着我们只考虑预测为正类的概率 a a a。如果预测 a a a 越接近 1,损失就越小;反之,预测越接近 0,损失越大。
-
当 y = 0 y = 0 y=0 时:
L ( y , a ) = − log ( 1 − a ) L(y, a) = -\log (1 - a) L(y,a)=−log(1−a)这意味着我们只考虑预测为负类的概率 1 − a 1 - a 1−a。如果预测 a a a 越接近 0(即 1 − a 1 - a 1−a 越接近 1),损失就越小;反之,预测 a a a 越接近 1,损失就越大。
3. 交叉熵损失函数的推导:
交叉熵损失函数的基本形式是:
L ( y , a ) = − [ y log a + ( 1 − y ) log ( 1 − a ) ] L(y, a) = -[y \log a + (1 - y) \log (1 - a)] L(y,a)=−[yloga+(1−y)log(1−a)]
这个公式是通过信息熵推导得到的。它衡量了真实标签 y y y 和预测输出 a a a 之间的不一致程度。公式的两部分分别对应着:
- 当 y = 1 y = 1 y=1 时,只考虑 log a \log a loga 部分,因为我们希望模型的预测 a a a 越接近 1 越好。
- 当 y = 0 y = 0 y=0 时,只考虑 log ( 1 − a ) \log (1 - a) log(1−a) 部分,因为我们希望 a a a 越接近 0 越好。
4. 交叉熵损失函数的性质:
- 凸性:交叉熵损失函数是一个凸函数,因此使用梯度下降等优化算法可以找到全局最小值。
- 惩罚错误预测:当模型的预测与真实标签差距较大时,交叉熵损失的值会迅速增大。因此,它可以有效惩罚错误的预测,并推动模型朝着正确预测的方向优化。
5. 交叉熵损失的意义:
交叉熵损失函数在神经网络的训练过程中非常重要,特别是在分类任务中。它结合了模型的预测输出和真实标签,提供了一个衡量预测准确性的标准。在反向传播中,我们通过最小化这个损失函数来调整模型的权重,从而提高模型的预测能力。
举个例子:
假设某个样本的真实标签为 y = 1 y = 1 y=1,而模型的预测为 a = 0.9 a = 0.9 a=0.9:
L ( y , a ) = − [ 1 log 0.9 + ( 1 − 1 ) log ( 1 − 0.9 ) ] = − log 0.9 ≈ 0.105 L(y, a) = -[1 \log 0.9 + (1 - 1) \log (1 - 0.9)] = -\log 0.9 \approx 0.105 L(y,a)=−[1log0.9+(1−1)log(1−0.9)]=−log0.9≈0.105
此时损失比较小,因为模型的预测接近真实值。
如果模型的预测为 a = 0.1 a = 0.1 a=0.1,则:
L ( y , a ) = − [ 1 log 0.1 + ( 1 − 1 ) log ( 1 − 0.1 ) ] = − log 0.1 = 1 L(y, a) = -[1 \log 0.1 + (1 - 1) \log (1 - 0.1)] = -\log 0.1 = 1 L(y,a)=−[1log0.1+(1−1)log(1−0.1)]=−log0.1=1
此时损失较大,说明预测误差大。
总结:
公式 8-11 定义的是交叉熵损失函数,用于衡量模型预测与真实标签之间的差异。通过最小化这个损失函数,我们可以不断调整模型的参数,使得模型的预测更加准确。交叉熵损失函数的特点在于它能够有效地惩罚错误的预测,并且是凸函数,适合用梯度下降进行优化。
相关文章:
解释说明)
交叉熵损失函数(Cross-Entropy Loss Function)解释说明
公式 8-11 的内容如下: L ( y , a ) − [ y log a ( 1 − y ) log ( 1 − a ) ] L(y, a) -[y \log a (1 - y) \log (1 - a)] L(y,a)−[yloga(1−y)log(1−a)] 这个公式表示的是交叉熵损失函数(Cross-Entropy Loss Function)&#…...

和外部机构API交互如何防止外部机构服务不可用拖垮调用服务
引言 在现代的分布式系统和微服务架构中,服务之间的通信往往通过API进行,尤其是在与外部机构或第三方服务进行交互时,更需要通过API实现功能的集成。然而,由于外部服务的可控性较差,其服务的不可用性(如响…...

自动猫砂盆真的有必要吗?买自动猫砂盆不看这四点小心害死猫。
现在越来越多铲屎官选择购买自动猫砂盆来代替自己给猫咪铲屎,可是自动猫砂盆真的有必要吗?要知道,在现在忙碌的生活中,有很多人因为工作上的忙碌而不小心忽视了猫咪,猫咪的猫砂盆堆满粪便,要知道猫砂盆一天…...

国外解压视频素材哪里找?五个海外解压视频素材网站推荐
国外解压视频素材哪里找?五个海外解压视频素材网站推荐 如果你正在寻找国外的解压视频素材,那么今天这篇文章一定能帮助你。无论是修牛蹄、洗地毯,还是切肥皂、玩解压游戏等,下面分享的几个网站都是你找到高质量海外解压视频素材…...
Android一个APP里面最少有几个线程
Android一个APP里面最少有几个线程 参考 https://www.jianshu.com/p/92bff8d6282f https://www.jianshu.com/p/8a820d93c6aa 线程查看 Android一个进程里面最少包含5个线程,分别为: main线程(主线程)FinalizerDaemon线程 终结者守护线程…...

位操作解决数组的花样遍历
文章目录 题目 一、思路: 二、代码 总结 题目 leetcodeT289 https://leetcode.cn/problems/game-of-life/description/ 一、思路: 这题思路很简单,对每个位置按照题目所给规则进行遍历,判断周围网格的活细胞数即可。但是题目要求…...

【面试宝典】深入Python高级:直戳痛点的题目演示(下)
目录 🍔 Python下多线程的限制以及多进程中传递参数的⽅式 🍔 Python是如何进⾏内存管理的? 🍔 Python⾥⾯如何拷⻉⼀个对象? 🍔 Python⾥⾯search()和match()的区别? 🍔 lambd…...

Hive数仓操作(十七)
一、Hive的存储 一、Hive 四种存储格式 在 Hive 中,支持四种主要的数据存储格式,每种格式有其特点和适用场景,不过一般只会使用Text 和 ORC : 1. Text 说明:Hive 的默认存储格式。存储方式:行存储。优点…...

工业和自动化领域常见的通信协议
在工业和自动化领域,有多种常见的通信协议,主要用于设备间的通信、数据传输和控制。 Modbus: 类型:串行通信协议用途:广泛用于工业自动化设备间的通信,如PLC、传感器和执行器。优点:简单、开放且…...

连夜爆肝收藏各大云服务新老用户优惠活动入口地址(内含免费试用1个月的地址),适用于小白,大学生,开发者,小企业老板....
具体请前往:云服务器优惠活动入口大全--收藏各主流云厂商的云服务器等系列产品的优惠活动入口,免费试用1个月活动入口,让新老用户都能根据使用场景和身份快速锁定优惠权益 经济下滑,被优化增多,大学生就业难࿰…...

SpringBoot+Redis+RabbitMQ完成增删改查
各部分分工职责 RabbitMQ负责添加、修改、删除的异步操作 Redis负责数据的缓存 RabbitMQ里面角色职责简单描述 RabbitMQ里面有几个角色要先分清以及他们的对应关系: 交换机、队列、路由键 交换机和队列是一对多 队列和路由键是多对多 然后就是消息的发送者&…...

【系统集成中级】线上直播平台开发项目质量管理案例分析
【系统集成中级】线上直播平台开发项目质量管理案例分析 一、案例二、小林在项目质量管理中存在的问题(一)计划阶段缺失(二)测试用例编制与执行问题(三)质量管理流程问题(四)质量保证…...

浪潮信息领航边缘计算,推动AI与各行业深度融合
在9月20日于安徽盛大召开的浪潮信息边缘计算合作伙伴大会上,浪潮信息指出,未来的计算领域将全面融入AI技术,特别是在企业边缘侧,智能应用特别是生成式人工智能应用正在迅速普及,这一趋势正引领边缘计算向边缘智算的方向…...

Koa2项目实战3 (koa-body,用于处理 HTTP 请求中的请求体)
以用户注册接口为例,需要在请求里携带2个参数:用户名(user_name)和密码(password)。 开发者需要在接口端,解析出user_name 、password。 在使用Koa开发的接口中,如何解析出请求携带…...

复盘20241012
1、 classpath "com.android.tools.build:gradle:8.5.1" 的版本 与distributionUrlhttps\://services.gradle.org/distributions/gradle-8.9-bin.zip的对应规则: Execution failed for task :app:compileDebugKotlin. 解决方案 切换 setting --> ot…...

泊松流负载均衡控制
目录 泊松流负载均衡控制 一、到达率λ 二、服务率μ 三、泊松流负载均衡控制 泊松流负载均衡控制 在探讨泊松流负载均衡控制时,我们主要关注的是到达率λ和服务率μ这两个核心参数。以下是对这两个参数及其在泊松流负载均衡控制中作用的详细解释: 一、到达率λ 定义:…...

3D打印矫形器市场报告:未来几年年复合增长率CAGR为10.8%
3D 打印矫形器是指使用 3D 打印技术制作的定制外部支撑装置。它们有助于稳定、引导、缓解或纠正肌肉骨骼状况,并根据个体患者的解剖结构进行设计,通常使用 3D 扫描和建模技术。3D 打印在矫形器方面的主要优势是能够生产精确适合患者解剖结构的定制装置&a…...
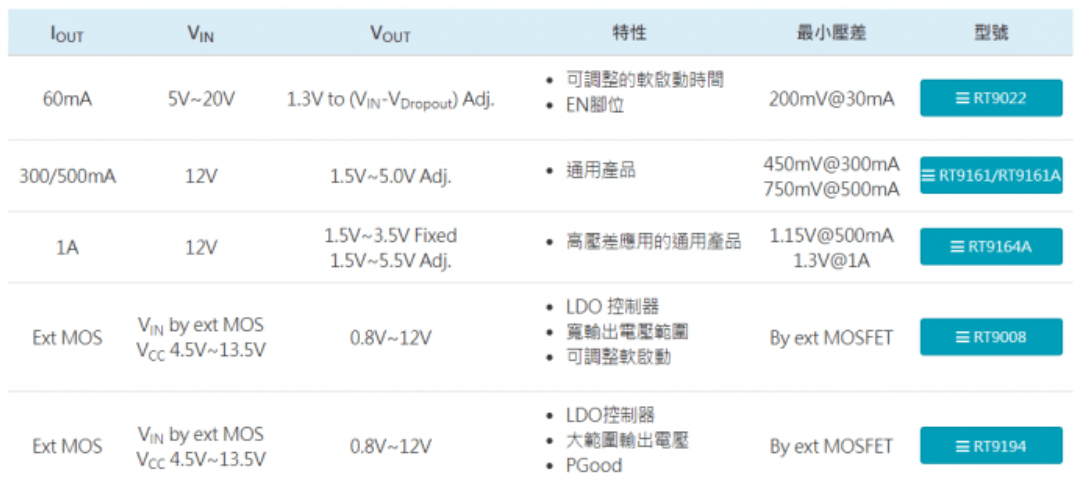
Richtek立锜科技线性稳压器 (LDO) 选型
一、什么是LDO? LDO也可称为低压差线性稳压器,适合从较高的输入电压转换成较低输出电压的应用,这种应用的功率消耗通常不是很大,尤其适用于要求低杂讯、低电流和输入、输出电压差很小的应用环境。 二、LDO的特性 LDO透过控制线性区调整管…...

Leetcode 前 k 个高频元素
使用最小堆算法来解决这道题目:相当于有一个容量固定为K的教室,只能容纳 K 个人,学生们逐个逐个进入该教室,当教室容量达到K人之后,每次进入一个新的学生后,我们将分数最低的学生(类似本题中的频率最低元素…...

[LeetCode] 面试题01.02 判定是否互为字符重拍
题目描述: 给定两个由小写字母组成的字符串 s1 和 s2,请编写一个程序,确定其中一个字符串的字符重新排列后,能否变成另一个字符串。 示例 1: 输入: s1 "abc", s2 "bca" 输出: true 示例 2&am…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...
