太阳能电池特性及其应用
中南民族大学-通信工程2024-大学物理下实验
目录
- 代码实现
- 结果显示
🛠工具使用
MarsCode(插件,集成在PyCharm);
python编程(豆包AI智能体)
💻编程改进
此处是用「Matplotlib」来作图,时间有限未能完全还原老师的要求。后面将尝试用「Seaborn」 。
「Seaborn」 继承了「Matplotlib」 的强大功能,同时提供了更高级的接口和更美观的默认样式;而且易于使用,代码简洁。
代码实现
# 太阳能电池特性
import math
import matplotlib.pyplot as plt
import numpy as np
from scipy import stats# 单晶硅
U = [0.0, 0.5, 1.0, 1.5, 2.0,2.2, 2.4, 2.6, 2.8, 3.0,3.2, 3.4, 3.6]
I1 = [0, 0.011, 0.022, 0.036, 0.051,0.058, 0.066, 0.074, 0.083, 0.094,0.107, 0.124, 0.145]
lnI1 = []
for i in range(len(I1)):if i == 0:continuelnI = math.log(I1[i])lnI1.append(lnI)# print(f'{lnI:.2f}')# 多晶硅
I2 = [0, 0.002, 0.005, 0.012, 0.023,0.029, 0.036, 0.045, 0.055, 0.067,0.082, 0.098, 0.116]
lnI2 = []
for i in range(len(I2)):if i == 0:continuelnI2.append(math.log(I2[i]))# print(# f"i{i+1:<2} = {I2[i]} lnI{i+1:<2} = {lnI:.2f}"# )# 非晶硅
I3 = [0, 0.001, 0.006, 0.050, 0.140,0.245, 0.396, 0.582, 0.807, 1.280,2.7, 6.1, 12.9]
lnI3 = []
for i in range(len(I3)):if i == 0:continuelnI3.append(math.log(I3[i]))# print(# f"i{i+1:<2} = {I3[i]} lnI{i+1:<2} = {lnI:.2f}"# )# 线性拟合求理想因子
# 转换为numpy数组
U = np.array(U[4:])
lnI1 = np.array(lnI1[3:])
lnI2 = np.array(lnI2[3:])
lnI3 = np.array(lnI3[3:])
# 绘制散点图
plt.subplot(3, 2, 2)
plt.scatter(U, lnI1, label='mc-Si')
plt.scatter(U, lnI2, label='pc-Si', marker='s')
plt.scatter(U, lnI3, label='a-Si', marker='^')
# 线性拟合
slope1, intercept1, r_value1, p_value1, std_err1 = stats.linregress(U, lnI1)
slope2, intercept2, r_value2, p_value2, std_err2 = stats.linregress(U, lnI2)
slope3, intercept3, r_value3, p_value3, std_err3 = stats.linregress(U, lnI3)
# 绘制线性拟合曲线
plt.plot(U, slope1 * U + intercept1, color='blue')
plt.plot(U, slope2 * U + intercept2, color='red')
plt.plot(U, slope3 * U + intercept3, color='green', linestyle='--')
plt.plot(U, lnI3, color='green')
# 添加图例和标签
plt.annotate(f"y={slope3:.2f}x{intercept3:.2f}\nR²={r_value3:.2f}", xy=(3.5, 1.6))
plt.annotate(f"y={slope2:.2f}x{intercept2:.2f}\nR²={r_value2:.2f}", xy=(3.5,-4))
plt.annotate(f"y={slope1:.2f}x{intercept1:.2f}\nR²={r_value1:.2f}", xy=(U[1],lnI1[1]))
plt.grid(True)
plt.title('Linear fitting for device\'s ideal factor')
plt.legend()
plt.xlabel('U/V')
plt.ylabel('lnI')
# 显示图形
print(f"Linear Fit Slope: {slope1} n:{26 / slope1}")
print(f"Linear Fit Slope: {slope2} n:{26 / slope2}")
print(f"Linear Fit Slope: {slope3} n:{26 / slope3}")# 太阳能电池暗态伏安特性
# 转换为numpy数组
U = [0.0, 0.5, 1.0, 1.5, 2.0,2.2, 2.4, 2.6, 2.8, 3.0,3.2, 3.4, 3.6]
U = np.array(U)
ax1 = plt.subplot(3, 2, 1)# 创建第一个 y 轴
ax1.scatter(U, I1, label='mc-Si') # 单晶硅
ax1.plot(U, I1) # 单晶硅
ax1.scatter(U, I2, marker='s',label='pc-Si')
ax1.plot(U, I2, ) # 多晶硅
ax1.set_xlabel('U/V')
ax1.set_ylabel('I/mA')# 创建第二个 y 轴
ax2 = plt.twinx()
ax2.scatter(U, I3, color='green', marker='^', label='a-Si')
ax2.plot(U, I3, color='green') # 非晶硅
# 添加箭头
# ax2.annotate("",xy=(3.5,5), xytext=(U[-2],I3[-2]), arrowprops=dict(facecolor='black'))ax1.grid(True)
lines, labels = ax1.get_legend_handles_labels()
lines2, labels2 = ax2.get_legend_handles_labels()
ax2.legend(lines + lines2, labels + labels2, loc='upper left')
plt.title('Solar cell dark state voltage-current characteristic')# 光照下太阳能电池输出特性
# 单晶硅
I11 = [0.061, 0.603, 1.492, 3.0, 5.8,7.2, 9.4, 11.1, 13.5, 16.5,20.0, 20.5, 20.5, 20.6, 20.8,20.9, 21.2, 21.2, 21.3, 21.5]
U11 = [6.11, 6.05, 6.01, 5.95, 5.84,5.77, 5.68, 5.61, 5.43, 5.00,4.02, 2.06, 1.66, 1.25, 0.84,0.43, 0.22, 0.14, 0.03, 0.01]
P1 = []
for i, u in zip(I11, U11):p = i * u# print(f"i = {i:.2f} U = {u:.2f} P = {p:.2f}")P1.append(p)# 多晶硅
I22 = [0.057, 0.573, 1.425, 2.7, 5.0,6.2, 8.0, 9.4, 11.4, 14.4,18.9, 24.3, 24.6, 24.7, 24.7,24.7, 24.6, 24.5, 24.5, 24.4]
U22 = [5.78, 5.77, 5.75, 5.35, 5.07,4.97, 4.82, 4.72, 4.58, 4.34,3.80, 2.46, 1.994, 1.504, 1.01,0.512, 0.264, 0.166, 0.04, 0.018]
P2 = []
for i, u in zip(I22, U22):p = i * u# print(f"i = {i:<5.2f} U = {u:.2f} P = {p:.2f}")P2.append(p)# 非晶硅
I33 = [0.031, 0.306, 0.760, 1.502, 3.0,3.7, 4.8, 5.6, 6.7, 8.2,9.6, 10.5, 10.6, 10.7, 10.6,10.7, 10.6, 10.7, 10.8, 10.8]
U33 = [3.1, 3.08, 3.06, 3.03, 2.97,2.93, 2.87, 2.81, 2.7, 2.47,1.93, 1.06, 0.852, 0.69, 0.428,0.22, 0.113, 0.072, 0.018, 0.008]
P3 = []
for i, u in zip(I33, U33):p = i * u# print(f"i = {i:<5.2f} U = {u:.2f} P = {p:.2f}")P3.append(p)# 输出功率和输出电压的关系
plt.subplot(3, 2, 5)
plt.scatter(U11, P1, label='mc-Si')
plt.plot(U11, P1)
plt.scatter(U22, P2, label='pc-Si', marker='s')
plt.plot(U22, P2)
plt.scatter(U33, P3, label='a-Si', marker='^')
plt.plot(U33, P3)plt.grid(True)
plt.legend()
plt.title('Output power and output voltage relationship')
plt.xlabel('U/V')
plt.ylabel('P/mW')# 光照下的太阳能电池输出特性
plt.subplot(3, 2, 6)
plt.scatter(U11, I11, label='mc-Si')
plt.plot(U11, I11)
plt.scatter(U22, I22, label='pc-Si', marker='s')
plt.plot(U22, I22)
plt.scatter(U33, I33, label='a-Si', marker='^')
plt.plot(U33, I33)plt.grid(True)
plt.legend(loc='upper right')
plt.title('Output characteristics of solar cells under illumination')
plt.xlabel('U/V')
plt.ylabel('I/mA')# 光照强度对开路电压的影响
I = [816, 323, 183, 122, 86, 67, 52, 42, 35, 29]
# 单晶硅
Uoc1 = [6.17, 5.82, 5.56, 5.41, 5.30, 5.22, 5.14, 5.08, 5.01, 4.96]
# 多晶硅
Uoc2 = [6.13, 5.82, 5.57, 5.40, 5.27, 5.18, 5.08, 5.01, 4.93, 4.86]
# 非晶硅
Uoc3 = [3.74, 3.38, 3.29, 3.22, 3.16, 3.11, 3.06, 3.01, 2.97, 2.93]plt.subplot(3, 2, 3)
plt.scatter(I, Uoc1, label='mc-Si')
plt.plot(I, Uoc1)
plt.scatter(I, Uoc2, label='pc-Si', marker='s')
plt.plot(I, Uoc2)
plt.scatter(I, Uoc3, label='a-Si', marker='^')
plt.plot(I, Uoc3)plt.grid(True)
plt.legend()
plt.title('Impact of light intensity on the open-circuit voltage')
plt.xlabel('I/(W/m²)')
plt.ylabel('Uoc/V')# 光照强度对短路电流的影响
# 单晶硅
Isc1 = [53.3, 24.7, 16.8, 9.2, 6.8, 5.1, 4.1, 3.4, 2.9, 2.4]
# 多晶硅
Isc2 = [91.8, 36.3, 22.2, 15.3, 11.2, 8.6, 6.7, 5.4, 4.4, 3.7]
# 非晶硅
Isc3 = [38.4, 19.0, 10.7, 7.0, 5.0, 3.8, 2.9, 2.3, 1.9, 1.6]plt.subplot(3, 2, 4)
plt.scatter(I, Isc1, label='mc-Si')
plt.plot(I, Isc1)
plt.scatter(I, Isc2, label='pc-Si', marker='s')
plt.plot(I, Isc2)
plt.scatter(I, Isc3, label='a-Si', marker='^')
plt.plot(I, Isc3)plt.grid(True)
plt.legend()
plt.title('Impact of light intensity on the short-circuit current')
plt.xlabel('I/(W/m²)')
plt.ylabel('Isc/mA')# 调整子图之间的间距
plt.subplots_adjust(hspace=0.5, wspace=0.3)# 显示图形
plt.show()结果显示

相关文章:

太阳能电池特性及其应用
中南民族大学-通信工程2024-大学物理下实验 目录 代码实现结果显示 🛠工具使用 MarsCode(插件,集成在PyCharm); python编程(豆包AI智能体) 💻编程改进 此处是用「Matplotlib」来作图…...

日语学习零基础生活日语口语柯桥外语学校|股票用日语怎么说?
在日语中,“股票”可以说: • 株(かぶ) 这是最常用的表达方式,直接表示“股票”。 例如: 株を買う - 买股票 株を売る - 卖股票 • 株式(かぶしき) 这个词也是“股票”的意…...
)
第2关:寻找一个序列中的第K小的元素(即第k小元问题)
[TOC]寻找一个序列中的第K小的元素(即第k小元问题) 对于给定的含有n(n<100)元素的无序序列,求这个序列中第k(1≤k≤n)小的元素。 任务描述 本关任务:编写一个能计算数组中的第k小的元素的小程序。 相关…...

docker 搭建 vue3 + vite
vue3发布了,今天就分享一下我使用docker 搭建 vue3 vite 开发环境。至于为什么使用docker搭建,因为多版本可以快速切换,和本地环境避免冲突。好了话不多说我们开始吧。 1. 准备资料 Docker Desktop wsl2 ubuntu 下载地址 : https://www.docker.…...
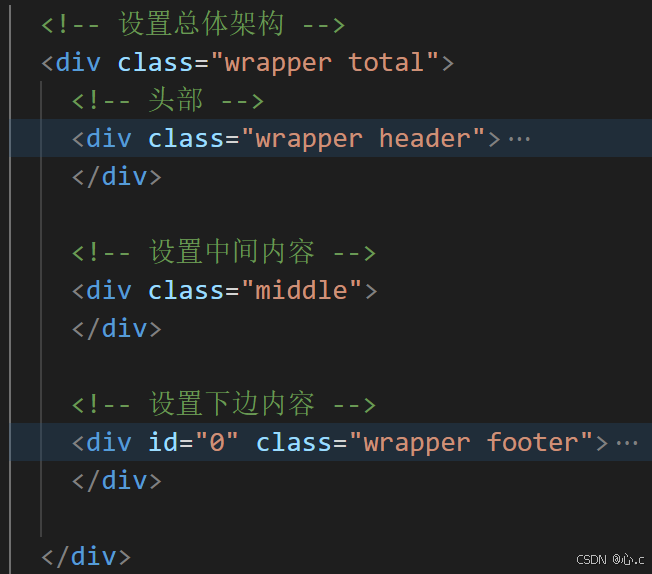
【网易云音乐】--源代码分享
最近写了一个网易云音乐的音乐实现部分,是通过JavaScript和jQuery实现的,具体效果大家可以参照下面的视频 源代码分享 - git地址: 网易云音乐源代码 下面将着重讲解一下音乐实现部分 视频有点模糊,不好意思,在b站上添加视频的时候…...
股市大涨下的会展业创新者
近期,股市涨势强劲有力,各大指数普遍上扬,市场活力空前。与此同时,伴随全球经济逐步复苏及会展行业不断发展,上市展览公司机遇与挑战并存。国内外市场需求持续增长拓展了广阔发展空间,但同时行业竞争愈发激…...
工具篇-完整的 Git 项目管理工具教程(在命令框中使用 Git、在 IDEA 中使用 Git)
🔥博客主页: 【小扳_-CSDN博客】 ❤感谢大家点赞👍收藏⭐评论✍ 文章目录 1.0 Git 概述 2.0 Git 的安装和配置 3.0 获取本地仓库 3.1 基础操作指令 3.2 分支 4.0 Git 远程仓库 4.1 创建远程仓库 4.2 配置 SSH 公钥 4.3 操作远程仓库 5.0 使用…...

关于Amazon Linux 2023的版本及包管理器
在亚马逊上创建EC2实例时,会看到有一个Amazon Linux镜像。 那这个镜像与其他Linux有什么关系和区别呢? 网站是介绍:Amazon Linux 2023 是基于 Linux 的现代化通用操作系统,提供 5 年的长期支持。它针对 AWS 进行了优化࿰…...

Java面向对象编程--高级
目录 一、static关键字 1.1 静态变量 1.2 静态内存解析 1.3 static的应用与练习 二、单例设计模式 2.1 单例模式 2.2 如何实现单例模式 三、代码块 3.1 详解 3.2 练习,测试 四、final关键字 五、抽象类与抽象方法 5.1 abstract 5.2 练习 六、接口 6.…...

Vert.x,Web - 静态资源/模板
静态资源 Vert.x-Web带有开箱即用的处理器(StaticHandler),用于处理静态Web资源(.html, .css, .js, …), 因此可以非常轻松地编写静态Web服务器。 默认静态文件目录为类路径下的webroot目录,对于maven的项目,按规范放在src/main/…...

OpenAI今天Open了一下:开源多智能体框架Swarm
来源 | 机器之心 毫无疑问,多智能体肯定是 OpenAI 未来重要的研究方向之一,前些天 OpenAI 著名研究科学家 Noam Brown还在 X 上为 OpenAI 正在组建的一个新的多智能体研究团队招募机器学习工程师。 就在几个小时前,这个或许还没有组建完成的新…...

车辆重识别(2021NIPS无分类器扩散指南)论文阅读2024/10/08
[1] CLASSIFIER-FREE DIFFUSION GUIDANCE(无分类器扩散指导) (NIPS 2021) 作者:Jonathan Ho & Tim Salimans 单位:Google Research, Brain team(谷歌团队) 摘要: 分类器指导是最近引入的一…...

JavaSE——认识异常
1.概念 在生活中,人有时会生病,在程序中也是一样,程序猿是一帮办事严谨、追求完美的高科技人才。在日常开发中,绞尽脑汁将代码写的尽善尽美,在程序运行过程中,难免会出现一些奇奇怪怪的问题。有时通过代码很…...

嵌入式数据结构中顺序栈用法
第一:嵌入式C语言中栈特点 栈是限制在一端进行插入操作和删除操作的线性表(俗称堆栈),允许进行操作的一端称为“栈顶”,另一固定端称为“栈底”,当栈中没有元素时称为“空栈”。特点 :后进先出(LIFO)。...

PE结构之绑定导入表
打印绑定导入表 //打印 绑定导入表 BOOL PrintBoundImport(__in char* m_fileName) {char* Filebuffer NULL;if (!GetFileBuffer(m_fileName, &Filebuffer)) return FALSE;PIMAGE_DOS_HEADER LPdosHeader NULL;PIMAGE_NT_HEADERS LPntHeader NULL;LPdosHeader (PIMAGE…...

【python学习】1-2 配置python系统环境变量
1.点击“我的电脑”右键,点击属性,点击“高级系统设置”,再点击环境变量。 2.选择“系统变量”中的Path后,点击编辑。 3.点击新建,添加如图两个路径,即是python安装的路径位置后,点击确定。...

日均千万订单的交易平台设计稿
业务背景 平台主要售卖电子商品和少量特定的实物商品。 经营模式,主要分为平台商家和自营店,自营店的流量占整个平台业务的50%以上,我负责自营店交易履约相关业务。 以前的架构,平台交易和履约中心是所有流量共享,在…...
如何在 iPad 上恢复已删除的历史记录?
iPad 配备了一个名为 Safari 的内置网络浏览器。这是一种在旅途中保持联系和浏览网页的强大且便捷的方式。但如果您不小心删除了浏览历史记录,则尝试恢复它可能会很令人沮丧。 幸运的是,您可以通过多种方法在 iPad 上恢复已删除的 Safari 历史记录。您应…...

Haar cascade训练人脸小模型做人脸辨别
代码讲解 1. 导入必要的库 import cv2 import os from pathlib import Path import shutil import numpy as np import loggingcv2: OpenCV 库,用于图像处理和计算机视觉。os: 提供了一种便携的方式使用操作系统依赖的功能。pathlib.Path: 提供了对象导向的路径处…...

DBA | 如何将 .mdf 与 .ldf 的数据库文件导入到SQL Server 数据库中?
[ 知识是人生的灯塔,只有不断学习,才能照亮前行的道路 ] 原文链接:DBA | 如何将 .mdf 与 .ldf 的数据库文件导入到SQL Server 数据库中? 如何将 (.mdf) 和 (.ldf) 的SQL Server 数据库文件导入到当前数据库中? Step 1.登录到 Sql Server 服…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...
