根据传入的文件流链接实现前端下载
后端传入一个下载的url,实现点击按钮,下载文件。
方式一:
通过window.open(“URL”, '_blank') 方式
PS:会打开一个新的页面
import React from 'react';const DownloadButton = () => {// window.open("URL", "_blank") 会在 新标签页 或 新窗口 中打开指定的 URLreturn (<button onClick={() => {window.open("URL","_blank")}}>Download File</button>);
};export default DownloadButton;
方式二:
创建一个标签,设置其href,实现下载:
import React from 'react';const DownloadButton = () => {const handleDownload = () => {const url = 'https://example.com/file-to-download'; // 替换为你的下载链接const a = document.createElement('a');a.href = url;a.download = ''; // 如果提供文件名,可以在这里设置,如 a.download = 'filename.ext';document.body.appendChild(a);a.click();document.body.removeChild(a); // 点击之后删除这个元素};return (<button onClick={handleDownload}>Download File</button>);
};export default DownloadButton;
相关文章:

根据传入的文件流链接实现前端下载
后端传入一个下载的url,实现点击按钮,下载文件。 方式一: 通过window.open(“URL”, _blank) 方式 PS:会打开一个新的页面 import React from react;const DownloadButton () > {// window.open("URL", "_…...

大数据新视界 --大数据大厂之大数据环境下的零信任安全架构:构建可靠防护体系
💖💖💖亲爱的朋友们,热烈欢迎你们来到 青云交的博客!能与你们在此邂逅,我满心欢喜,深感无比荣幸。在这个瞬息万变的时代,我们每个人都在苦苦追寻一处能让心灵安然栖息的港湾。而 我的…...

基于springboot的高校招生系统(含源码+sql+视频导入教程+文档+PPT)
👉文末查看项目功能视频演示获取源码sql脚本视频导入教程视频 1 、功能描述 基于springboot的高校招生系统1拥有两种角色:管理员和用户 管理员:学生管理、专业管理、报名管理、录取通知管理、招生公告管理等 用户:登录注册、报…...

【C++设计模式】行为型模式:观察者模式
文章目录 行为型模式:观察者模式 行为型模式:观察者模式 观察者模式定义了一种一对多的依赖关系:它让一个主题(被观察者)对象关联多个观察者对象,并且当主题对象的状态发生变化时,它会主动通知…...

本篇5K,立志最细,FreeRtos中的信号量Semaphore教程详解!!!
前言:本篇教程,参考韦东山,开发文档,连接放在最后 目录 Semaphore基本概念 二值信号量(Binary Semaphore) 计数信号量(Couting Semaphore) 互斥信号量(Mutex&…...

【Postman】接口测试工具使用
干就完啦 Postman发送get请求案例1: Postman发送post请求案例2 Postman发送其他请求Postman测试实战 学习目标:能够使用Postman发送get/post/put/delete请求并获取响应结果 Postman发送get请求 首先postman是一款接口调试工具,支持win&…...

springboot 整合 rabbitMQ(1)
目录 一、MQ概述 二、MQ的优势和劣势 三、常见的MQ产品 RabbitMQ使用步骤 第一步:确保rabbitmq启动并且可以访问15672 第二步:导入依赖 第三步:配置 auto自动确认 manual手工确认(推荐使用!可以防止消息丢失&a…...
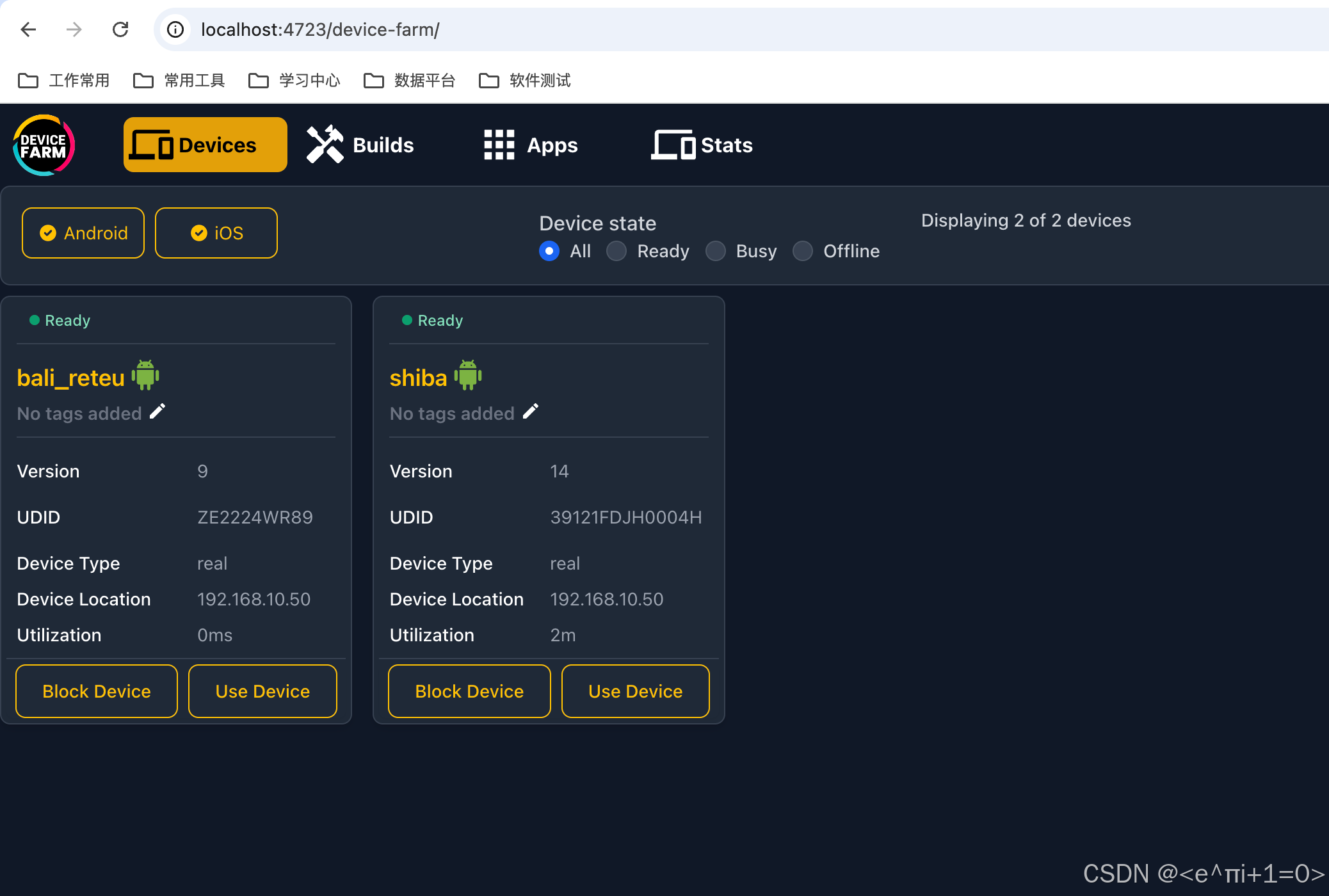
Appium Device Farm安装教程
环境要求:Appium version ≥ 2.4.X 安装appium npm install -g appium2.11.3 如果安装提示如下问题 npm error code EEXIST npm error syscall rename npm error path /Users/wan/.npm/_cacache/tmp/d5787519 npm error dest /Users/wan/.npm/_cacache/content-…...

异常、基类
异常 人生和世界总是充满着意外,争议、冲突和战争似乎是人类必然经历的过程。程序执行也有不满的时候。 不同编程语言的异常 Ada/Modula-3是早期引入异常处理的语言。 C语言没有标准意义的异常,使用goto或setjmp模拟错误或异常发生时的处理流程。 C/Java…...
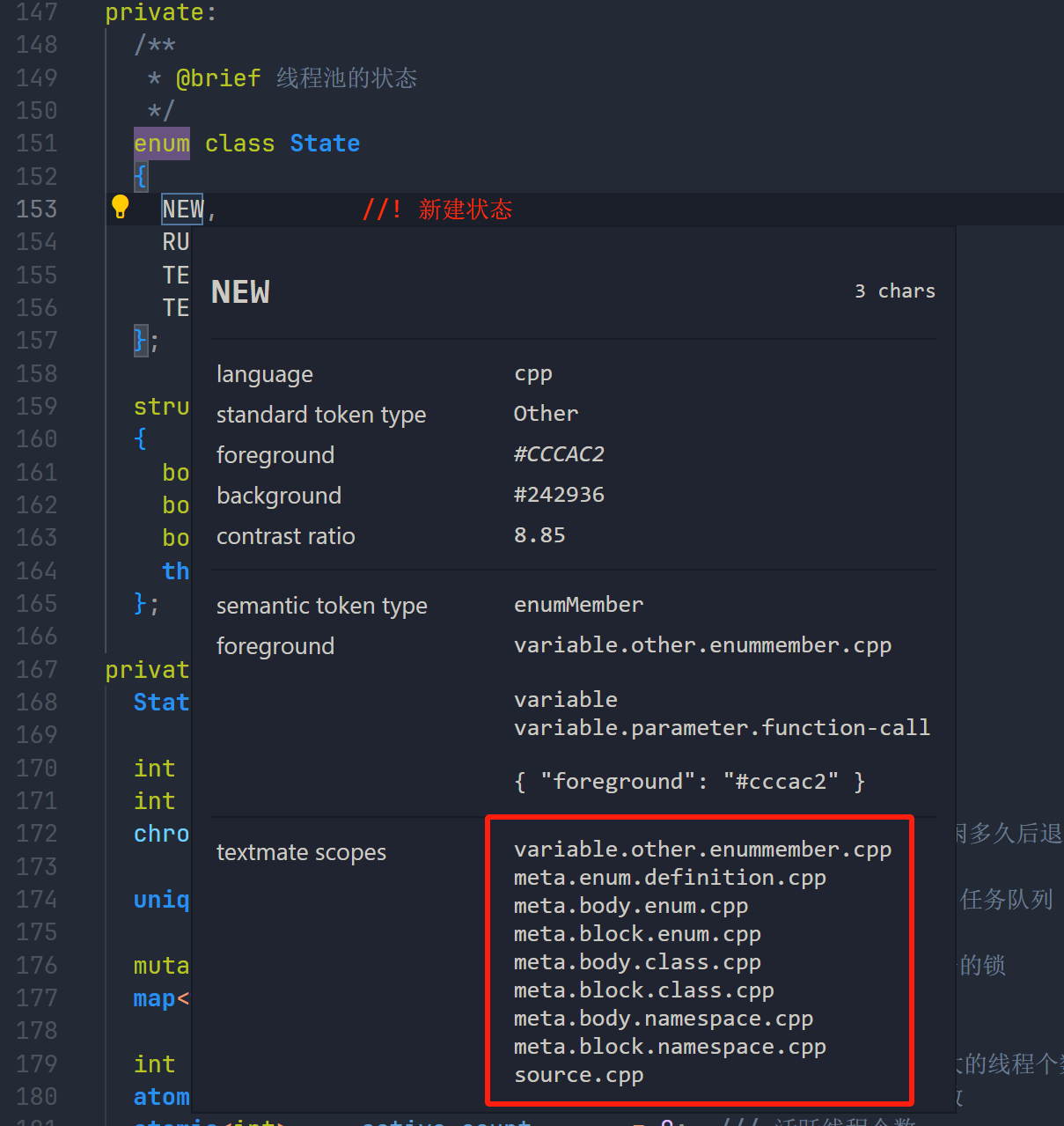
VScode 自定义代码配色方案
vscode是一款高度自定义配置的编辑器, 我们来看看如何使用它自定义配色吧 首先自定义代码配色是什么呢? 看看我的代码界面 简而言之, 就是给你的代码的不同语义(类名, 函数名, 关键字, 变量)等设置不同的颜色, 使得代码的可读性变强. 其实很多主题已经给出了定制好的配色方案…...
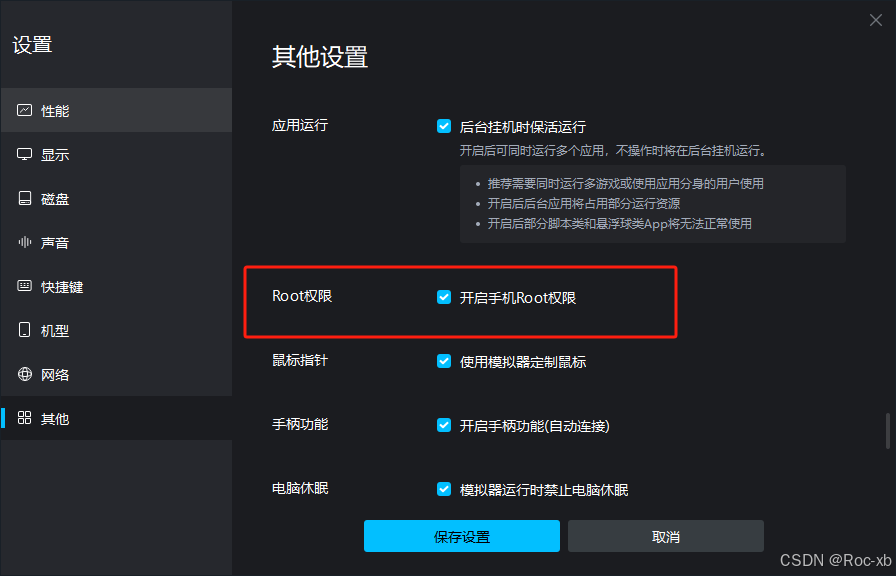
MuMu模拟器12 KitsumeMask安装教程
这里是引用"> 在MuMu模拟器上安装KitsumeMask的时候遇到安装失败的情况。 一、下载APK安装包 如果你没有apk安装包可以通过下面的百度网盘进行下载 通过网盘分享的文件:KitsumeMask 链接: https://pan.baidu.com/s/1yeq3I6BsUD7J6uI-bnk-Vw?pwd=7n3v 提取码: 7n3v 二…...

Perforce静态分析工具2024.2新增功能:Helix QAC全新CI/CD集成支持、Klocwork分析引擎改进和安全增强
Perforce Helix QAC和Klocwork的最新版本对静态分析工具进行了重大改进,通过尽早修复错误、降低开发成本和加快发布速度,使开发团队实现左移。 本文中,我们将概述2024.2版本的新特性和新功能。 CI/CD和左移以实现持续合规性 现代软件开发实…...

太阳能电池特性及其应用
中南民族大学-通信工程2024-大学物理下实验 目录 代码实现结果显示 🛠工具使用 MarsCode(插件,集成在PyCharm); python编程(豆包AI智能体) 💻编程改进 此处是用「Matplotlib」来作图…...

日语学习零基础生活日语口语柯桥外语学校|股票用日语怎么说?
在日语中,“股票”可以说: • 株(かぶ) 这是最常用的表达方式,直接表示“股票”。 例如: 株を買う - 买股票 株を売る - 卖股票 • 株式(かぶしき) 这个词也是“股票”的意…...
)
第2关:寻找一个序列中的第K小的元素(即第k小元问题)
[TOC]寻找一个序列中的第K小的元素(即第k小元问题) 对于给定的含有n(n<100)元素的无序序列,求这个序列中第k(1≤k≤n)小的元素。 任务描述 本关任务:编写一个能计算数组中的第k小的元素的小程序。 相关…...

docker 搭建 vue3 + vite
vue3发布了,今天就分享一下我使用docker 搭建 vue3 vite 开发环境。至于为什么使用docker搭建,因为多版本可以快速切换,和本地环境避免冲突。好了话不多说我们开始吧。 1. 准备资料 Docker Desktop wsl2 ubuntu 下载地址 : https://www.docker.…...
【网易云音乐】--源代码分享
最近写了一个网易云音乐的音乐实现部分,是通过JavaScript和jQuery实现的,具体效果大家可以参照下面的视频 源代码分享 - git地址: 网易云音乐源代码 下面将着重讲解一下音乐实现部分 视频有点模糊,不好意思,在b站上添加视频的时候…...
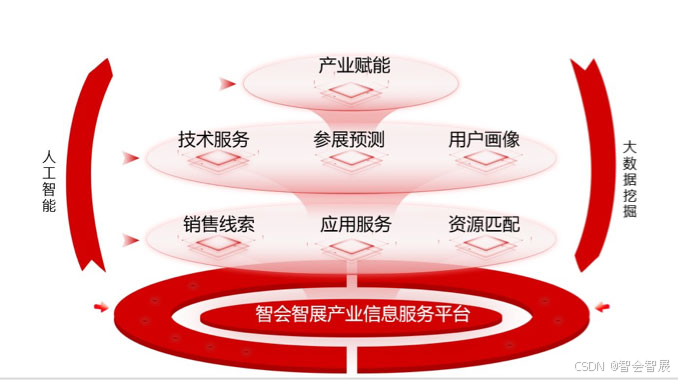
股市大涨下的会展业创新者
近期,股市涨势强劲有力,各大指数普遍上扬,市场活力空前。与此同时,伴随全球经济逐步复苏及会展行业不断发展,上市展览公司机遇与挑战并存。国内外市场需求持续增长拓展了广阔发展空间,但同时行业竞争愈发激…...
工具篇-完整的 Git 项目管理工具教程(在命令框中使用 Git、在 IDEA 中使用 Git)
🔥博客主页: 【小扳_-CSDN博客】 ❤感谢大家点赞👍收藏⭐评论✍ 文章目录 1.0 Git 概述 2.0 Git 的安装和配置 3.0 获取本地仓库 3.1 基础操作指令 3.2 分支 4.0 Git 远程仓库 4.1 创建远程仓库 4.2 配置 SSH 公钥 4.3 操作远程仓库 5.0 使用…...

关于Amazon Linux 2023的版本及包管理器
在亚马逊上创建EC2实例时,会看到有一个Amazon Linux镜像。 那这个镜像与其他Linux有什么关系和区别呢? 网站是介绍:Amazon Linux 2023 是基于 Linux 的现代化通用操作系统,提供 5 年的长期支持。它针对 AWS 进行了优化࿰…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...
