[Halcon矩阵] 通过手眼标定矩阵计算相机旋转角度
- 📢博客主页:https://loewen.blog.csdn.net
- 📢欢迎点赞 👍 收藏 ⭐留言 📝 如有错误敬请指正!
- 📢本文由 丶布布原创,首发于 CSDN,转载注明出处🙉
- 📢现在的付出,都会是一种沉淀,只为让你成为更好的人✨
文章预览:
- 一. 理解手眼标定矩阵
- 二. 拆解手眼标定矩阵
一. 理解手眼标定矩阵
手眼标定矩阵通常是一个齐次变换矩阵,它包含了旋转、平移、缩放和可能的其他变换信息。这个矩阵可以将一个点从机械手坐标系变换到相机坐标系,或者相反。
二. 拆解手眼标定矩阵
1、提取旋转矩阵
-
旋转矩阵是一个正交矩阵,它的行和列都是单位向量且彼此正交。
-
在二维情况下,旋转矩阵(22)通常表示为:[cosθ,-sinθ,sinθ,cosθ](这里不是14矩阵,而是2*2矩阵)
-
可以通过计算手眼标定矩阵的左上角2x2子矩阵[a,b,c,d]的行列式来确定是否包含缩放或剪切变换。
1)如果行列式等于1,即|a,b,c,d| = ab - cd = 1,则矩阵只包含旋转;
2)如果不等于1,即|a,b,c,d| = ab - cd ≠ 1,则矩阵可能还包含缩放或剪切。 -
在没有缩放和剪切的情况下,可以通过对左上角2x2子矩阵进行正交化来提取旋转矩阵。
2、提取缩放矩阵
-
缩放矩阵是一个对角矩阵,它的对角线元素表示了各个方向上的缩放比例。
-
在二维情况下,缩放矩阵通常表示为:S=[Sx,0,0,Sy]
-
可以通过计算手眼标定矩阵的左上角2x2子矩阵的每个元素的绝对值来确定缩放比例。然而,这种方法可能受到旋转和剪切的影响,因此更准确的方法是通过SVD(奇异值分解)或QR分解来提取缩放比例。
3、提取剪切矩阵
- 剪切矩阵表示了坐标轴之间的倾斜程度。
- 在二维情况下,剪切矩阵通常不是对角矩阵,但可以通过计算手眼标定矩阵的左上角2x2子矩阵的非对角线元素来确定剪切程度。
- 然而,剪切变换通常不是手眼标定中的标准变换,因此可能需要额外的步骤来识别和提取剪切矩阵。这通常涉及到更复杂的数学处理,如矩阵的极分解或QR分解。
这也为我们从一个包含缩放和旋转效果的变换矩阵中提取出纯粹的旋转部分,然后计算旋转角度提供思路:可以按照以下步骤进行(假设只考虑旋转和缩放,没有剪切和平移):
三. 实战演练(提取旋转角度)
以该手眼标定矩阵的左上角2x2子矩阵为例:
M = [ M 11 M 12 M 21 M 22 ] = [ − 8.56361 e − 03 2.24152 e − 05 1.07640 e − 05 8.55496 e − 03 ] (1) M = \tag{1} \left [ \begin{matrix} M_{11} & M_{12}\\ M_{21} & M_{22}\\ \end{matrix}\right ] =\left [ \begin{matrix} -8.56361e-03 & 2.24152e-05\\ 1.07640e-05 & 8.55496e-03\\ \end{matrix}\right ] M=[M11M21M12M22]=[−8.56361e−031.07640e−052.24152e−058.55496e−03](1)
1、 很明显可以看出,由于|M11M22 - M12M21| ≠ 1,所以该矩阵还包含缩放或剪切。
2、消除缩放效果(矩阵归一化)*:
1)对于 2×2 矩阵,我们可以选择任一行的范数来作为缩放因子,将旋转矩阵归一化,即将第一列的向量单位化。
这样可以消除矩阵的缩放效果:
S 1 = ( M 11 ) 2 + ( M 21 ) 2 = ( − 8.56361 ∗ 1 0 − 3 ) 2 + ( 1.07640 ∗ 1 0 − 5 ) 2 ≈ 0.00856361 \text{S}_1 = \sqrt{(M_{11})^2 + (M_{21})^2} = \sqrt{(-8.56361 * 10^{-3})^2 + (1.07640* 10^{-5})^2} ≈ 0.00856361 S1=(M11)2+(M21)2=(−8.56361∗10−3)2+(1.07640∗10−5)2≈0.00856361
S 2 = ( M 12 ) 2 + ( M 22 ) 2 = ( 2.24152 ∗ 1 0 − 5 ) 2 + ( 8.55496 ∗ 1 0 − 3 ) 2 ≈ 0.00855496 \text{S}_2 = \sqrt{(M_{12})^2 + (M_{22})^2} = \sqrt{(2.24152 * 10^{-5})^2 + (8.55496* 10^{-3})^2} ≈ 0.00855496 S2=(M12)2+(M22)2=(2.24152∗10−5)2+(8.55496∗10−3)2≈0.00855496
取: S = S 1 + S 2 2 = 0.008559285 (2) S =\tag{2} \frac{S_1+S_2}{2} = 0.008559285 S=2S1+S2=0.008559285(2)
3、归一化矩阵:将矩阵除以缩放因子,消除缩放效果:
M ’ = M S = [ − 8.56361 ∗ 1 0 − 3 / 0.008559285 2.24152 ∗ 1 0 − 5 / 0.008559285 1.0764 ∗ 1 0 − 5 / 0.008559285 8.55496 ∗ 1 0 − 3 / 0.008559285 ] = [ − 1.0005 0.00262 0.00126 0.9995 ] (3) M’ =\frac{M}{S} = \tag{3} \left [\begin{matrix} -8.56361 * 10^{-3} /0.008559285 & 2.24152* 10^{-5} /0.008559285\\ 1.0764* 10^{-5} /0.008559285 & 8.55496 * 10^{-3} /0.008559285\\ \end{matrix}\right] =\left [\begin{matrix} -1.0005 & 0.00262\\ 0.00126 & 0.9995\\ \end{matrix}\right] M’=SM=[−8.56361∗10−3/0.0085592851.0764∗10−5/0.0085592852.24152∗10−5/0.0085592858.55496∗10−3/0.008559285]=[−1.00050.001260.002620.9995](3)
4、由于m12′(0.00262) 与m21′ (0.00126)并不相同,表明矩阵中不仅仅含有旋转矩阵,还包含了剪切矩阵,剪切变换会改变图形的形状,使其在某些方向上拉伸或压缩,但不像缩放那样均匀地影响所有方向。
M ’ = R ⋅ K = [ c o s ( θ ) − s i n ( θ ) s i n ( θ ) c o s ( θ ) ] × [ 1 k x k y 1 ] = [ − 1.0005 0.00262 0.00126 0.9995 ] (4) M’ =\tag{4}R⋅K = \left [ \begin{matrix} cos(\theta) & -sin(\theta) \\ sin(\theta) & cos(\theta)\\ \end{matrix}\right ] × \left[ \begin{matrix} 1 & kx \\ ky & 1\\ \end{matrix}\right ] = \left [\begin{matrix} -1.0005 & 0.00262\\ 0.00126 & 0.9995\\ \end{matrix}\right] M’=R⋅K=[cos(θ)sin(θ)−sin(θ)cos(θ)]×[1kykx1]=[−1.00050.001260.002620.9995](4)
其中,kx表示水平剪切因子,决定了沿y轴的移动量,ky表示垂直剪切因子,决定了沿x轴的移动量。
5、计算旋转角度:
如果忽略剪切带来的影响,可以根据归一化后的矩阵 M′的元素,我们可以计算旋转角度 :
θ = a r c t a n 2 ( m 21 ′ , m 11 ′ ) = a r c t a n 2 ( 0.00126 , − 1.0005 ) = 3.14033 = 179.928 ° (5) θ=\tag{5}arctan2(m_{21}^′,m_{11}^′) = arctan2(0.00126,-1.0005) = 3.14033 = 179.928° θ=arctan2(m21′,m11′)=arctan2(0.00126,−1.0005)=3.14033=179.928°(5)
由m11′为负可知, 机械手坐标系与相机坐标系X方向为相反的关系,所以实际角度偏差为180 - 179.928 = 0.072°
PS:arctan2 函数是计算两个数的商(y/x)的反正切值,但考虑了这两个数所在的象限,(y/x)= (0.00126/-1.0005)在第二象限。
拓展:

| 下雨天,最惬意的事莫过于躺在床上静静听雨,雨中入眠,连梦里也长出青苔。 |
相关文章:

[Halcon矩阵] 通过手眼标定矩阵计算相机旋转角度
📢博客主页:https://loewen.blog.csdn.net📢欢迎点赞 👍 收藏 ⭐留言 📝 如有错误敬请指正!📢本文由 丶布布原创,首发于 CSDN,转载注明出处🙉📢现…...

推荐几本编程入门书目
对于编程入门,推荐以下几本书籍,这些书籍覆盖了不同的编程语言,适合零基础的学习者逐步掌握编程基础: 1. 《Python编程快速上手——让繁琐工作自动化》 特点:以简单易懂的方式介绍了Python的基础知识和编程概念&#…...
- 提升方法)
每天一个数据分析题(五百零五)- 提升方法
提升方法(Boosting),是一种可以用来减小监督式学习中偏差的机器学习算法。基于Boosting的集成学习,其代表算法不包括? A. Adaboost B. GBDT C. XGBOOST D. 随机森林 数据分析认证考试介绍:点击进入 题…...

华为云ECS部署DR模式的LVS
1 概述 LVS是linux内核模块,用于4层的负载均衡,它有多个工作模式,例如NAT模式、DR模式。 DR模式的数据流是这样的: client ---> Director Server(即LVS服务器,带VIP) ---> Real Serve…...
)
如何在 Jupyter Notebook 执行和学习 SQL 语句(上)
在Jupyter Notebook中使用SQL,你可以通过以下步骤创建一个数据库并连接到该数据库: 1. 安装SQLite和SQLAlchemy SQLite 是一个轻量级的数据库系统,适合本地小型项目。SQLAlchemy 是一个强大的数据库连接工具,可以在Jupyter中方便…...

数据结构-5.7.二叉树的层次遍历
一.演示: 1.初始化队列: 2.根结点入队: 3.判断队列是否为空,此时有根结点,说明不为空,则队头结点即根结点出队并访问,再先进它的左结点,最后进它的右结点: 4.之后对进来…...
RISC-V知识点目录
分支预测 分支预测概述https://blog.csdn.net/zhangshangjie1/article/details/136947089?sharetypeblogdetail&sharerId136947089&sharereferPC&sharesourcezhangshangjie1&spm1011.2480.3001.8118分支指令的方向预测https://blog.csdn.net/zhangshangjie1/a…...
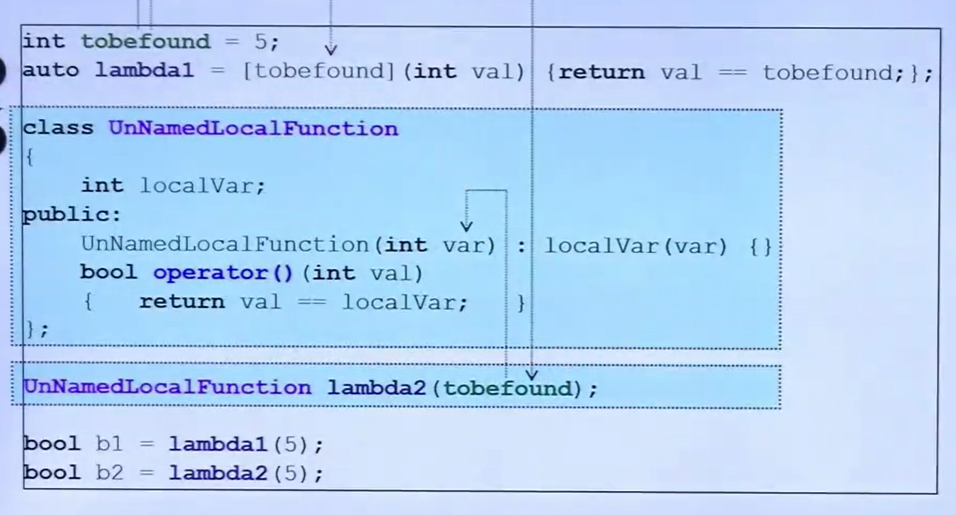
C++11 新特性 学习笔记
C11 新特性 | 侯捷C11学习笔记 笔者作为侯捷C11新特性课程的笔记进行记录,供自己查阅方便 文章目录 C11 新特性 | 侯捷C11学习笔记1.Variadic TemplatesC11支持函数模板的默认模板参数C11在函数模板和类模板中使用可变参数 可变参数模板1) 可变参数函数模板2) 可变…...

Go 语言中的格式化占位符
在 Go 语言中,fmt 包提供了大量的格式化占位符,用于格式化输出不同类型的数据。选择合适的占位符,可以确保输出的内容格式正确、清晰易懂。 常见的占位符: 基本类型 %v:按值的默认格式输出。适用于任何类型。%v&…...
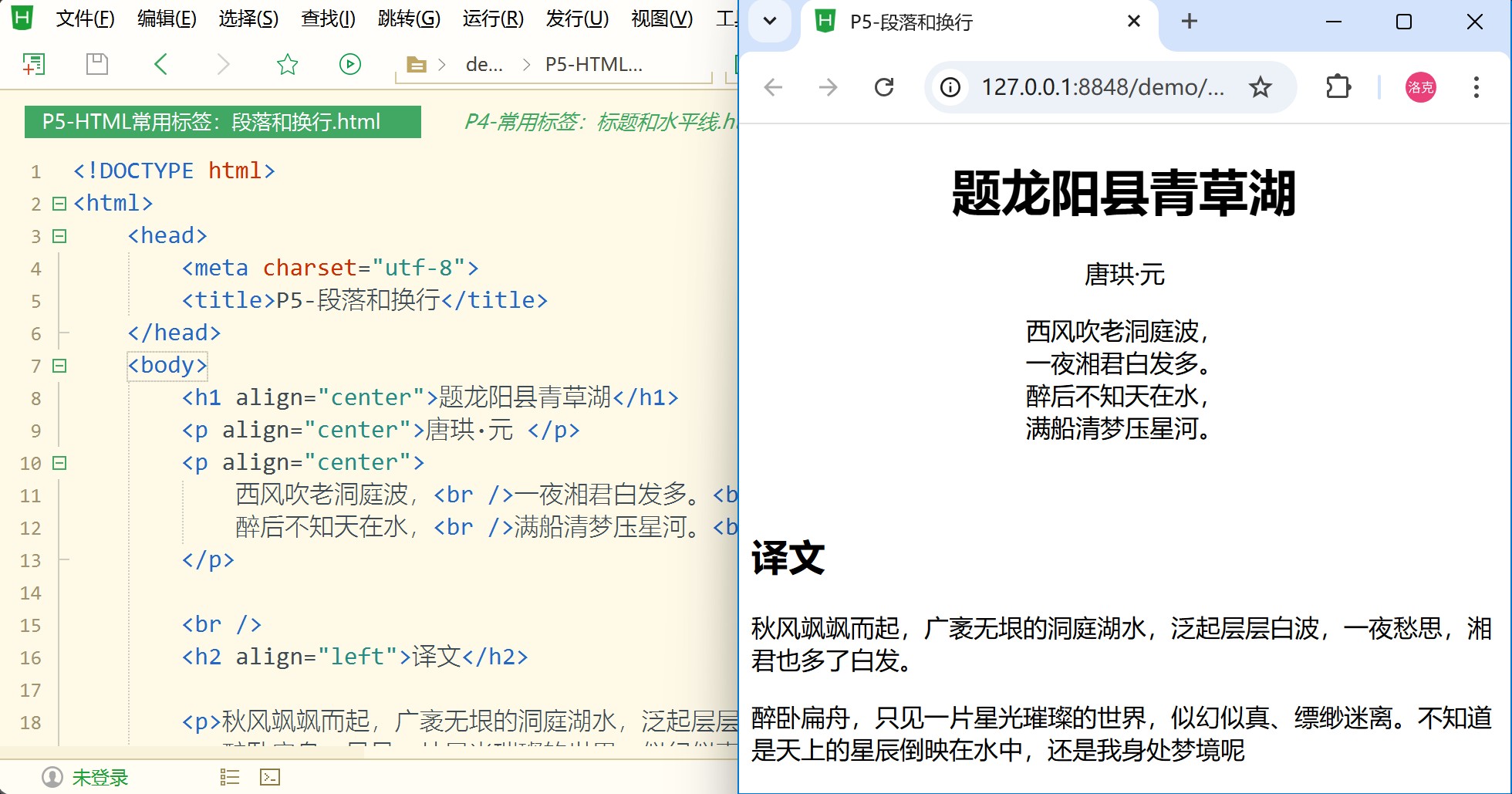
QD1-P5 HTML 段落标签(p)换行标签(br)
本节视频 www.bilibili.com/video/BV1n64y1U7oj?p5 本节学习 HTML 标签: p标签 段落br标签 换行 一、p 标签-段落 1.1 使用 p 标签划分段落 <p>段落文本</p>示例 <!DOCTYPE html> <html><head><meta charset"…...

Django的模板语法
Django的模板语法 1、初步认识2、原理 1、初步认识 本质上:在HTML中写一些占位符,由数据对这些占位符进行替换和处理。 在views.py中用字典(键值对)的形式传参,在html文件中用两个花括号来显示单独的值 列表、元组等数…...

【在Linux世界中追寻伟大的One Piece】信号捕捉|阻塞信号
目录 1 -> 信号捕捉初识 2 -> 阻塞信号 2.1 -> 信号其他相关常见概念 2.2 -> 在内核中的表示 2.3 -> sigset_t 2.4 -> 信号集操作函数 2.5 -> sigprocmask 2.6 -> sigpending 3 -> 捕捉信号 3.1 -> 内核如何实现信号的捕捉 3.2 ->…...

信息系统运维管理方案,运维建设文档,运维平台建设方案,软件硬件中间件运维方案,信息安全管理(原件word,PPT,excel)
建设方案目录: 1、智慧运维系统建设背景 2、智慧运维系统建设目标 3、智慧运维系统建设内容 4、智慧运维系统建设技术 5、智慧运维系统建设流程 6、智慧运维系统建设收益 企业对运维管理的需求: 1、提高运维效率:降低运维成本,提高…...

多元统计实验报告内容
1 实验内容 实验目的: 利用R软件进行一些简单的数学运算,通过对简单统计量函数的操作了解R语言的基本操作过程,从而对R语言形成初步的认识。 实验项目名称: R语言软件的安装。R语言中赋值语句的练习。 在R中<-表示赋值,c()表示数组,X1<-c()即表示将一组数据赋…...

使用机器学习边缘设备的快速目标检测
论文标题:Fast Object Detection with a Machine Learning Edge Device 中文标题:使用机器学习边缘设备的快速目标检测 作者信息: Richard C. Rodriguez, MSDA Information Systems and Cyber Security Department, The University of Tex…...

Anthropic的CEO达里奥·阿莫迪(Dario Amodei)文章传达他对AI未来的乐观展望
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...

Human-M3 多模态姿态估计数据集-初步解读
文章概述(个人总结):该论文重点提出一个用于人体姿态估计的RGB+点云数据集,针对该多模态数据集,作者阐述了数据集的收集、数据标注以及该数据集的特点。并提出了一个简单的多模态3D人体姿态估计算法,对比其他模型,该方法性能较好。最后总结了该数据集和该方法的限制。 …...

python爬虫 - 进阶正则表达式
🌈个人主页:https://blog.csdn.net/2401_86688088?typeblog 🔥 系列专栏:https://blog.csdn.net/2401_86688088/category_12797772.html 目录 前言 一、匹配中文 (一)匹配单个中文字符 (二…...

静态路由和nqa 联动实验
nqa 配置 1 test 断端口 很明显是切换到备机上了...

golang用any类型去接收前端传的数字类型的值,类型断言为float64
在 Go 中,使用 any 类型接收前端传来的数字时,通常会发现其被类型断言为 float64。这是因为在 JSON 解码的过程中,Go 的 encoding/json 包会将数字解析为 float64。但如果你在结构体中指明字段为 int 类型,框架会根据字段类型进行…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...

Python异步编程:深入理解协程的原理与实践指南
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 持续学习,不断…...
