网络流C++
网络流问题及其应用
网络流问题是图论中的一个经典问题,应用于交通调度、物流配送、计算机网络等领域。它通过模型化图中的流量传递过程,解决从源点传递流量到汇点的最优流量分配问题。本文将介绍网络流的基本概念、几种经典算法,并通过一个具体例题来帮助理解。
一、网络流的基本概念
网络流问题通常表示为一个有向图,图中的节点和边构成了一个流动网络。流量从源点(Source)通过有向边流向汇点(Sink),每条边都有一定的容量限制。
- 节点(Vertex):表示网络中的站点,如城市、服务器。
- 边(Edge):节点间的有向线,表示资源的传递方向。
- 容量(Capacity):每条边上的最大流量限制。
基本术语
- 源点(Source):流量的起始点,记为
S。 - 汇点(Sink):流量的终点,记为
T。 - 流量守恒:对于除源点和汇点之外的所有节点,流入的总流量等于流出的总流量。
- 流量限制:流过每条边的流量不能超过其容量。
示例
考虑一个运输网络,城市之间有道路连接,每条道路的运输能力有限。目标是从某个城市(源点)出发,将尽可能多的物资送到另一个城市(汇点)。这个问题可以通过网络流模型求解。
二、经典算法介绍
1. Ford-Fulkerson算法
Ford-Fulkerson算法是求解最大流问题的经典方法,其核心思想是反复找到从源点到汇点的增广路径,并通过这条路径增加流量。
- 增广路径:从源点到汇点的路径,且所有边上都有剩余容量。
- 步骤:
- 找到一条增广路径。
- 沿着这条路径增加流量,更新边的剩余容量。
- 反复进行,直到无法找到增广路径为止。
2. Edmonds-Karp算法
Edmonds-Karp算法是Ford-Fulkerson算法的改进版本,使用**广度优先搜索(BFS)**来寻找增广路径,保证每次找到的都是最短路径。
- 时间复杂度:O(V * E^2),其中
V为节点数,E为边数。
3. Dinic算法
Dinic算法通过构建分层网络,进一步优化了最大流的求解。每次流量增加时,按层次推进,减少增广路径的重复使用。
- 时间复杂度:O(V^2 * E),特别适用于稀疏图。
三、网络流的实际应用
1. 交通网络优化
在交通系统中,最大流算法可以用于计算最大通过量,以避免交通堵塞,优化道路的使用效率。
2. 电力网络
在电力系统中,电流从发电站(源点)流向用户(汇点)。通过最大流模型,可以优化电力输送,提高电网的效率。
3. 数据传输
在计算机网络中,数据包通过有限带宽的链路传输。使用网络流算法可以规划最佳路径,最大化数据流量,避免网络拥堵。
4. 图像分割
网络流算法在计算机视觉领域也有应用,如图像分割问题。通过最大流技术,可以将图像划分为前景和背景,形成清晰的分割结果。
四、例题:最大流问题
题目:
给定一个有向图,包含N个节点和M条边,每条边有一个容量C,求从源点S到汇点T的最大流量。
输入:
- 第一行:两个整数
N(节点数)和M(边数)。 - 接下来
M行:每行三个整数u, v, C,表示从节点u到节点v有一条容量为C的有向边。
输出:
- 从源点
S到汇点T的最大流量。
示例:
输入:
4 5
1 2 40
1 3 20
2 3 10
2 4 25
3 4 30
输出:
40
五、C++代码实现
下面是使用Edmonds-Karp算法实现最大流问题的C++代码:
#include <iostream>
#include <vector>
#include <queue>
#include <climits>
#include <cstring>
using namespace std;const int MAXN = 100; // 假设最多有100个节点
int capacity[MAXN][MAXN]; // 容量矩阵
int flow[MAXN][MAXN]; // 当前流量矩阵
int parent[MAXN]; // 用于记录增广路径
int n, m; // 节点数和边数// 使用BFS查找增广路径
bool bfs(int source, int sink) {memset(parent, -1, sizeof(parent));queue<int> q;q.push(source);parent[source] = source;while (!q.empty()) {int u = q.front();q.pop();for (int v = 0; v < n; v++) {if (parent[v] == -1 && capacity[u][v] - flow[u][v] > 0) {parent[v] = u;if (v == sink) return true;q.push(v);}}}return false;
}// 使用Edmonds-Karp算法求解最大流
int edmonds_karp(int source, int sink) {int max_flow = 0;while (bfs(source, sink)) {int path_flow = INT_MAX;// 找到增广路径上的最小剩余容量for (int v = sink; v != source; v = parent[v]) {int u = parent[v];path_flow = min(path_flow, capacity[u][v] - flow[u][v]);}// 更新路径上每条边的流量for (int v = sink; v != source; v = parent[v]) {int u = parent[v];flow[u][v] += path_flow;flow[v][u] -= path_flow;}// 增加总流量max_flow += path_flow;}return max_flow;
}int main() {cin >> n >> m;memset(capacity, 0, sizeof(capacity));memset(flow, 0, sizeof(flow));// 读取图的边for (int i = 0; i < m; i++) {int u, v, c;cin >> u >> v >> c;u--; v--; // 假设节点编号从1开始,需要转为从0开始capacity[u][v] = c;}// 源点为0,汇点为n-1cout << edmonds_karp(0, n - 1) << endl;return 0;
}
代码说明:
- 使用BFS寻找增广路径。
- 在增广路径上找到最小剩余容量,并更新每条边的流量。
- 使用Edmonds-Karp算法求解最大流,输出结果。
六、总结
网络流问题在多个领域中都有重要应用。通过理解最大流的概念和算法,可以解决复杂的流量调度和优化问题。在本文中,我们介绍了Ford-Fulkerson、Edmonds-Karp等算法,并通过一个例题展示了如何在C++中实现这些算法。
相关文章:

网络流C++
网络流问题及其应用 网络流问题是图论中的一个经典问题,应用于交通调度、物流配送、计算机网络等领域。它通过模型化图中的流量传递过程,解决从源点传递流量到汇点的最优流量分配问题。本文将介绍网络流的基本概念、几种经典算法,并通过一个…...
RTC -
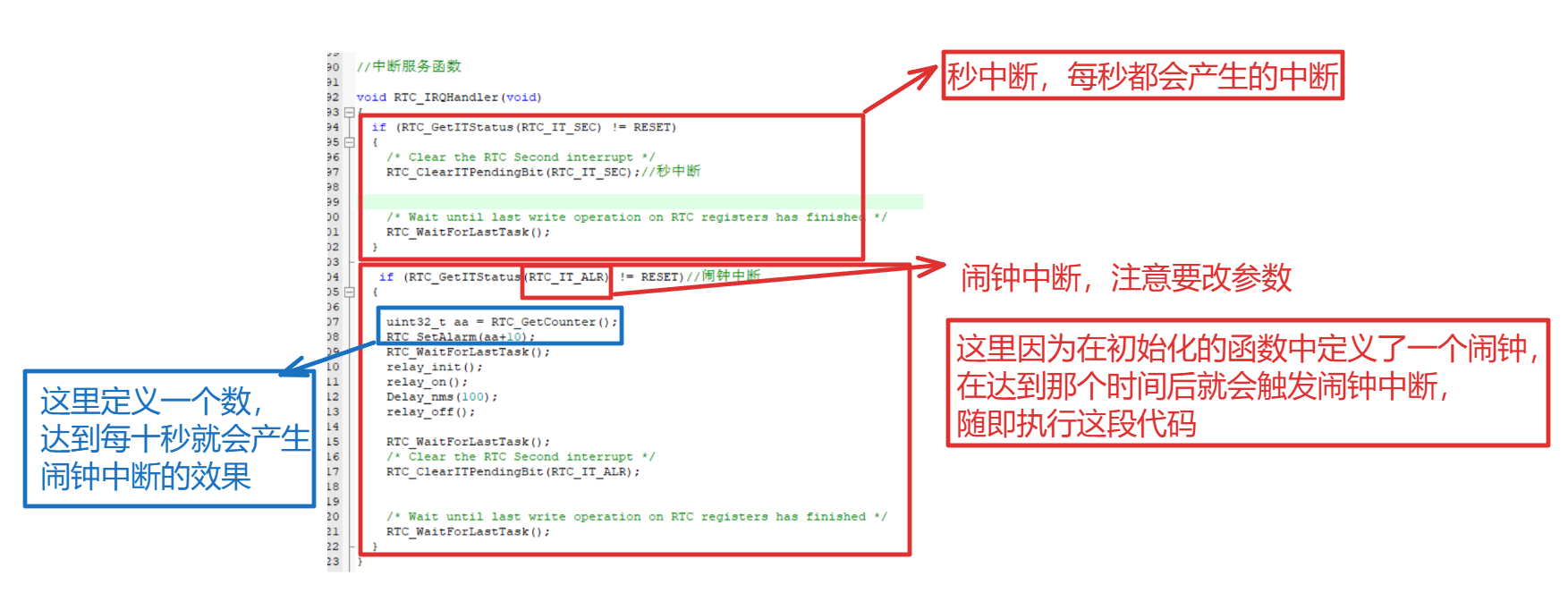
RTC 目录 RTC 回顾 RTC 如何实现RTC制作一个时钟日历 代码编写 rtc.c完整代码 模块开发的步骤: 1、找文档 2、 在文档里面找通信方式,通信过程(协议) 3、代码> -- 前面学的是模块的开发,串口类,I…...

图像处理中常用的统计矩
目录 原点矩中心矩常用的统计矩偏度(Skewness)定义解释 峰度(Kurtosis)定义解释 统计矩的应用MATLAB相关函数 原点矩(Moment about the Origin)和中心矩(Central Moment)是概率论和数…...
Ubuntu 详解| Ubuntu ssh| Ubuntu apt命令大全| Ubuntu性能优化| Ubuntu换镜像源
Ubuntu 是Debian开源linux系统体系下的子分支之一 Debian-ubuntu 和它一样的还有 kali(一款渗透测试软件) Debian-kali 小白参考 :Centos 7.9 安装 图解版 小白必看 最新_centos7.9-CSDN博客文章浏览阅读2.5k次,点赞…...

Linux安全命令(Linux Security Commands)
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 本人主要分享计算机核心技…...

2024最新版安装教程!Python安装+PyCharm安装使用教程!!(非常简单)
Python下载安装 一、进入Python官网首页,下载最新版的Python 官方网址:Download Python | Python.org 鼠标悬浮在Downloads,选择最新版本 注意:由于Python官网服务器设立在国外,所以下载速度非常慢,我这…...

C++:STL:vector类常用函数介绍(附加部分重要函数模拟实现)
cplusplus.com/reference/vector/vector/https://cplusplus.com/reference/vector/vector/ vector在实际中非常的重要,在实际中我们熟悉常见的接口就可以,有了string的基础,vector其实大体使用方法上二者是类似的: 这里我们先给…...

[工程构建] 使用 pkg-config 的 cmake 模板
可执行文件 # 1) cmake basic cmake_minimum_required(VERSION 3.12) #cmake version check set(CXX_STANDARD 17) #c standard version)# 2) project info #auto generated variables as below: #PROJECT_NAME: "hello" #hello_BINARY_DIR: build root dir #hello_…...

MATLAB 注释快捷键
matlab 前言单行注释多行注释 快捷键使用菜单 前言 单行注释 % 这是一个单行注释 x 10; % 这是另一个单行注释多行注释 %{ 这是一个多行注释 它可以包含多行文本 x 10; % 这行代码也会被注释掉 %}快捷键 在 MATLAB 编辑器中,可以使用快捷键来快速注释和取消注…...

8.优化存储过程的性能(8/10)
优化存储过程的性能 1.引言 存储过程是数据库系统中预先编写好的SQL语句集合,它们被保存在数据库服务器上,可以在需要时被调用执行。存储过程的使用可以提高数据库操作的效率,减少网络通信,并且可以封装复杂的逻辑,使…...

Django发送邮件代理服务器配置
根路由下配置 MAIL_BACKEND django.core.mail.backends.smtp.EmailBackend EMAIL_HOST smtp.qq.com EMAIL_HOST_USER 66897079qq.com EMAIL_HOST_PASSWORD aavlzhzvqorbcahcEMAIL_PORT 465 EMAIL_USE_SSL True发送邮件 message "<p>尊敬的用户您好ÿ…...

uniapp__微信小程序使用秋云ucharts折线图双轴
1、子组件 <template><view class"charts-box"><qiun-data-charts type"line":opts"computedOpts":chartData"chartData"/></view> </template><script> export default {props: {chartData: {t…...
)
云原生运维 - 旅程(简约版)
1. 入门阶段 理论学习: 了解云计算和容器技术的基本概念。学习Docker基础知识,包括容器创建、镜像管理等。阅读Kubernetes官方文档的入门部分,了解Kubernetes的核心概念。 实操练习: 安装Docker环境。运行你的第一个Docker容器…...

2014年国赛高教杯数学建模B题创意平板折叠桌解题全过程文档及程序
2014年国赛高教杯数学建模 B题 创意平板折叠桌 某公司生产一种可折叠的桌子,桌面呈圆形,桌腿随着铰链的活动可以平摊成一张平板(如图1-2所示)。桌腿由若干根木条组成,分成两组,每组各用一根钢筋将木条连接…...

PyCharm打开及配置现有工程(详细图解)
本文详细介绍了如何利用Pycharm打开一个现有的工程,其中包括编译器的配置。 PyCharm打开及配置现有工程 1、打开工程2、配置编译器 1、打开工程 双击PyCharm软件,点击左上角 文件 >> 打开(O)… 选中想要打开的项目之后点击“确定” 2、配置编译器…...

CSP-J
CSP那些事儿 OI赛制是啥OI赛制下的CCF-CSPCSP简介CSP-J考试(仅山东)考试时间考试地点考试结构 写在最后有趣的代码: OI赛制是啥 OI赛制,不详细说了,就是一股脑做好几个题,一起提交的比赛(通俗易…...

Linux系统:Linux中ln命令用法
ln命令功能 将一个文件或目录在同一个文件系统或者另一个不同的文件系统的某个位置建立一个链接,类似windows系统中的超链接,这样当我们在链接处访问被链接的目录或文件时就可以通过此链接来访问,不必要再进入要访问的文件系统中。 建立链接…...

在SpringBoot+VUE中 实现登录-RSA的加密解密
步骤-先理清楚在动手 前端首先调用后端的公钥接口,在前端加密密码传输至后端登录接口后端用私钥解密码拿着用户名去数据库查询出来的盐值加密的 密码1用私钥解密密码登录密码加盐值得到 密码2比较密码1与密码2,相同则登录成功,跳转首页|其他页面 前端实…...

基于Android11简单分析audio_policy_configuration.xml
开篇先贴上一个高通的例子,后续基于此文件做具体分析。 1 <?xml version"1.0" encoding"UTF-8" standalone"yes"?> 2 <!-- Copyright (c) 2016-2019, The Linux Foundation. All rights reserved 3 Not a Contribut…...

kafka-manager修改zookeeper端口号后启动仍然连接2181端口
问题描述: zookeeper默认端口号修改为了2182,kafka-manager的配置文件application.conf中也已经修改了zkhosts为新的端口号,然而启动kafka-manger时报错连接连接超时,发现连接的还是2181端口,很奇怪?&…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...
