【数据结构笔记】搜索树
二叉搜索树
任一节点x的左/右子树中,所有非空节点均不大于(不小于)x
- 必须是所有的非空节点,仅左右孩子不够(左孩子的右孩子可能很大)
- 一棵二叉树是二叉搜索树当且仅当中序遍历序列是单调非降序列
两棵二叉搜索树等价当且仅当他们有相同的中序遍历序列(上下可变,左右不乱)
- 换言之,构成两棵二叉搜索树的元素相同
等价变换zig、zag
- zig:右单旋转
- zag:左单旋转
变换后仍保持二叉搜索树的性质

(《算法导论》练习13.2-2)在任何一棵有n个结点的二叉搜索树中,恰有n-1种可能的旋转。
度为2的节点有2种转法,度为1的节点有1种转法,从而每种旋转对应一条边,共n-1条边。
(《算法导论》练习13.2-4)任何一棵含n个结点的二叉搜索树可以通过O(n)次旋转,转变为其他任何一棵含n个结点的二叉搜索树。
对于任何含n个结点的二叉搜索树,若某节点有左孩子,就右旋,如此会消除一个左孩子-父节点关系,而最多只有n-1个上述的左孩子-父节点关系,从而经至多n-1次旋转就能将其变为一条右链,而左右旋都是可逆的,转变只需要以该右链作为中介。
【2014-THU-Fin】由同一组共n个词条构成的任意两棵BST,经O(logn)次zig和zag旋转之后,必可相互转换。(×)
搜索
中序遍历操作
内部变量_hot指向搜索的终止位置的父节点
- 如果命中,就是目标节点的父节点
- 如果未命中,就是目标节点如果存在时的父节点
API返回搜索的终止位置
- 如果命中,就是目标节点
- 如果未命中,就是_hot的子哨兵节点
时间复杂度O(h)
插入
先搜索,让_hot指向将增加孩子的节点,再添加子节点
从插入的节点开始,向上更新节点高度
时间复杂度O(h)
删除
单子节点删除
直接把删除节点换成其以子唯一节点为根的子树
删除时利用搜索接口确定节点位置的过程给出当前_hot,它是向上更新节点高度的起点
双子节点删除
用在右子树中的直接后继替换删除节点,原来直接后继是度不为2的节点,化为单子节点删除
_hot设为原来直接后继的父节点,它是向上更新节点高度的起点
/******************************************************************************************
* BST节点删除算法:初除位置x所指癿节点(全局静态模板函数,适用亍AVL、Splay、RedBlack等各种BST)
* 目标x在此前经查找定位,并确认非NULL,故必删除成功;与searchIn不同,调用之前不必将hot置空
* 返回值指向实际被删除节点的接替者,hot指向实际被删除节点的父亲——二者均有可能是NULL
******************************************************************************************/
template <typename T>
static BinNodePosi(T) removeAt (BinNodePosi(T)& x, BinNodePosi(T)& hot) {BinNodePosi(T) w = x; //实际被摘除的节点,初值同xBinNodePosi(T) succ = NULL; //实际被删除节点的接替者if (!HasLChild(*x)) { //若*x的左子树为空,则可succ = x = x->rc; //直接将*x替换为其右子树}else if (!HasRChild(*x)){ //若右子树为空,则可succ = x = x->lc; //对称地处理——注意:此时succ != NULL}else { //若左右子树均存在,则选择x的直接后继作为实际被摘除节点,为此需要w = w->succ(); //(在右子树中)找到*x的直接后继*wswap(x->data, w->data); //交换*x和*w的数据元素BinNodePosi(T) u = w->parent;succ = w->rc; //w一定无左孩子,化为单节点的仅有右孩子情形((u == x) ? u->rc : u->lc) = succ;//如果u是x,即x是w的父节点,此时w在u的右子树中//若不然,因w是x的直接后继,此时w在u的左子树中}hot = w->parent; //记录实际被删除节点的父亲if (succ) {succ->parent = hot; //并将被删除节点的接替者与hot相联}release(w->data);release(w);return succ; //释放被摘除节点,返回接替者
} //release()负责释放复杂结构,与算法无直接关系,见代码包时间复杂度O(h)
平衡二叉搜索树
理想平衡树:n个节点,树高为⌊log_2n⌋的二叉树
适度平衡:n个节点,树高为渐进O(logn)的二叉树
- 经过单次修改操作,最多只有O(logn)处不再满足适度平衡性条件
- 可在O(logn)时间内,使这些不适度平衡处重新适度平衡
AVL树
节点v的平衡因子balFac(v) = height(lc(v)) - height(rc(v))
AVL条件:AVL树中所有节点满足|balFac(v)| <= 1
高度为h的AVL树至少含fib(h+3)-1个节点,进而n个节点的AVL树树高是O(logn)的。
【2012-THU-Fin】将[1481,1992]区间内的整数逐一插入到空AVL树中,最后该AVL树的高度是(CD)
A.7
B.8
C.9
D.10
E.以上都不对
共512=2^9个元素,至少为9。fib(13)-1=232,也可能是10。
失衡与重平衡
记UT(x)是因对节点x的操作而不满足AVL条件的节点集,下假设调整前UT(x)非空
插入失衡
UT(x)中的元素都是x的祖先,其不低于x的祖父节点,且可能一直失衡到根节点
重平衡自下而上逐个修正


右旋转

左旋转

左-右旋转

右-左旋转

- 如果节点g的X孩子的Y子树插入导致的失衡
- X=Y,在g做X旋转
- X!=Y,先在X孩子做X旋转,再在g做Y旋转
- 如果插入导致了旋转调整,那么本次插入不改变树高
每种旋转都是就地O(1)时间复杂度算法,每次将消除一个节点的失衡,而AVL树树高是O(logn)的,即最多O(logn)次旋转,时间复杂度共计O(logn)
删除失衡
UT(x)只有1个节点,但可能出现节点的替换(自下而上的失衡传播);任何进入UT(x)的节点失衡前后高度不变(要是失衡了,删除部分来自更低的部分,但高度取决于更高的子树)
删除导致的旋转调整不保证不改变树高,树高可能降低
时间复杂度O(logn)
“3+4”平衡重构

单次重构为就地O(1)时间复杂度算法(不计更新高度)
【2014-THU-Fin】设在某新节点插入AVL树后(尚待平衡化时),最低失衡节点为g。若此时g的左、右孩子的平衡因子分别为-1和0,则应通过(C)旋转使之重新恢复平衡。
A.zig
B.zig+zag
C.zag+zig
D.zag
E.不确定
【2016-THU-Fin】若AVL树插入元素的过程中发生了旋转操作,则树高必不变。(√)
【2016-THU-Fin】如果元素理想随机,那么对二叉搜索树做平衡化处理,对改进其渐进时间复杂度并没有什么实质的作用。(×)
伸展树
红黑树
B树
相关文章:

【数据结构笔记】搜索树
二叉搜索树 任一节点x的左/右子树中,所有非空节点均不大于(不小于)x 必须是所有的非空节点,仅左右孩子不够(左孩子的右孩子可能很大)一棵二叉树是二叉搜索树当且仅当中序遍历序列是单调非降序列 两棵二叉…...

如何使用UART(STM32 HAL库)
UART (通用异步收发器)是在 USART (通用同步异步收发器)基础上裁剪掉了同步通信功能,只剩下异步通信功能。关于通信和串口的基本知识,可参见文章《串口通信简介-CSDN博客》和《数据通信的一些基础概念-CSDN…...

星巴克英语
用流利的英文点星巴克 一杯咖啡 英文中文英文中文barista咖啡师coffee maker家用咖啡机cup sleeve杯套coffee stirrer咖啡棒coffee cup lid咖啡杯盖子straw吸管latte art咖啡拉花for here内用to go外带 例句: Could I have a cup sleeve for my coffee , please…...

权重衰减与暂退法——paddle部分
权重衰减与暂退法——paddle部分 本文部分为paddle框架以及部分理论分析,torch框架对应代码可见权重衰减与暂退法torch import paddle print("paddle version:",paddle.__version__)paddle version: 2.6.1当我们谈论机器学习模型的性能时,经…...

golang获取当天最小的时间,以DateTime的string格式返回
推荐学习文档 golang应用级os框架,欢迎stargolang应用级os框架使用案例,欢迎star案例:基于golang开发的一款超有个性的旅游计划app经历golang实战大纲golang优秀开发常用开源库汇总想学习更多golang知识,这里有免费的golang学习笔…...

2025 - 中医学基础 - 考研 - 职称
2025 - 中医学基础 - 考研 - 职称 第1章 中医学导论 1.中医学的指导思想是()( ) [单选] A.阴阳学说 B.五行学说 C.精气学说 D.整体观念 E.辨证论治 正确答案: D 2.中医学的理论核心是&…...

Pandas库
一、安装 Pandas是一个基于Python构建的专门进行数据操作和分析的开源软件库,它提供了高效的数据结构和丰富的数据操作工具。 安装 pip install pandas 二、核心数据结构 Pandas库中最常用的数据类型是Series和DataFrame: Series:一维数…...

Qt网络编程: 构建高效的HTTP文件下载器
文章目录 注意事项调用示例在使用Qt进行HTTP下载时,通常会使用QNetworkAccessManager类来管理HTTP请求和响应。这个类提供了进行网络请求的能力,包括下载文件。下面是使用Qt进行HTTP下载的一个示例,以及在实现时应考虑的一些注意事项。 注意事项 1.错误处理 始终检查QNetwo…...

Python 将Word, Excel, PDF和PPT文档转换为OFD格式
目录 使用工具 Python 将Word文档转换为OFD Python 将Excel文档转换为OFD Python 将PDF文档转换为OFD Python 将PPT文档转换为OFD OFD(Open Fixed-layout Document)是中国国家标准的电子文档格式,主要用于政府、金融等行业的正式文档传输…...
QD1-P21-P22 CSS 基础语法、注释、使用方法
本节学习:CSS 基础语法和注释,以及如何使用CSS定义的样式。 本节视频 https://www.bilibili.com/video/BV1n64y1U7oj?p21 CSS 基本语法 CSS(层叠样式表)的基本语法相对简单,由选择器和一组包含在花括号 {} 中的声…...

您是否也在寻找免费的 PDF 编辑器工具?10个备选PDF 编辑器工具
您是否也在寻找免费的 PDF 编辑器工具? 如果是,那么您在互联网上处于最佳位置! 本指南中提到的所有 10 大免费 PDF 编辑器工具都易于使用,可以允许您添加文本、更改图像、添加图形、填写表格、添加签名等等。 因此,…...
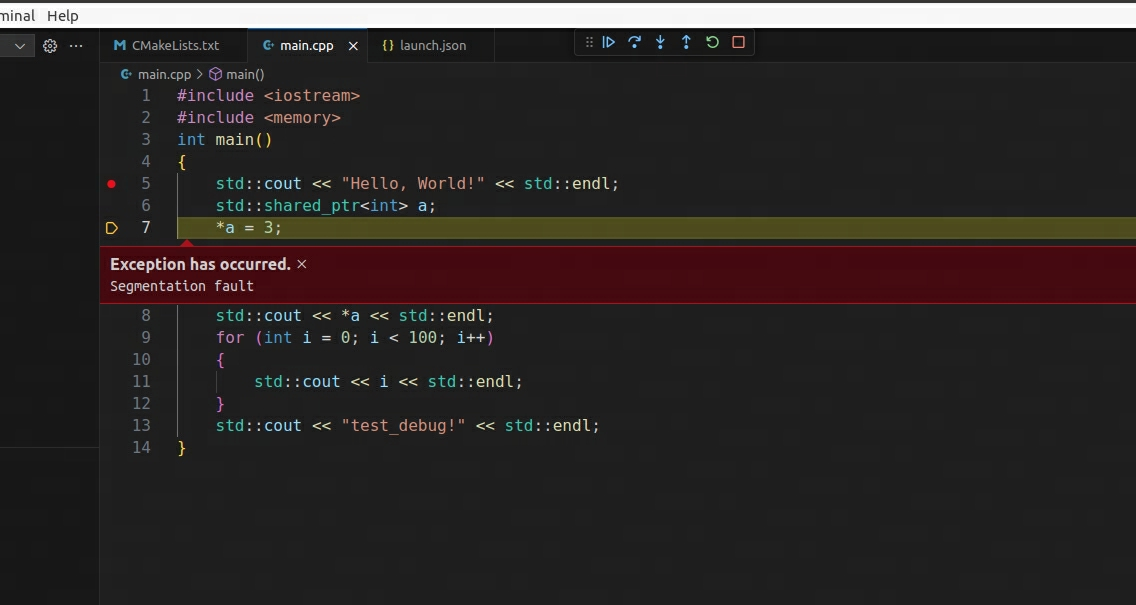
C++调试方法(Vscode)(一) ——本地调试
初学者在调试一段代码的时候,经常出于不明原因,写出bug,导致程序崩溃。但是定位崩溃的地方时,往往采用简单而朴素的方法:即采用cout或者printf进行输出。这种方式既原始,又低效。一个合格的工程师应该是通过…...

C语言 | Leetcode C语言题解之第460题LFU缓存
题目: 题解: /* 数值链表的节点定义。 */ typedef struct ValueListNode_s {int key;int value;int counter;struct ValueListNode_s *prev;struct ValueListNode_s *next; } ValueListNode;/* 计数链表的节点定义。 其中,head是数值链表的头…...
P4-隐性事实查询L2)
【AI论文精读12】RAG论文综述2(微软亚研院 2409)P4-隐性事实查询L2
AI知识点总结:【AI知识点】 AI论文精读、项目、思考:【AI修炼之路】 P1,P2,P3 四、隐性事实查询(L2) 4.1 概述 ps:P2有四种查询(L1,L2,L3,L4&…...

SpringBoot中间件Docker
Docker(属于C/S架构软件) 简介与概述 1.Docker 是一个开源的应用容器引擎,基于 Go 语言 并遵从 Apache2.0 协议开源。 Docker 可以让开发者打包他们的应用以及依赖包到一个轻量级、可移植的容器中,然后发布到任何流行的 Linux …...

计算机毕设选题推荐【大数据专业】
计算机毕设选题推荐【大数据专业】 大数据专业的毕业设计需要结合数据的采集、存储、处理与分析等方面的技能。为帮助同学们找到一个适合且具有实践性的选题,我们为大家整理了50个精选的毕设选题。这些选题涵盖了大数据分析、处理技术、可视化等多个方向࿰…...
Bootstrap 4 多媒体对象
Bootstrap 4 多媒体对象 引言 Bootstrap 4 是目前最受欢迎的前端框架之一,它提供了一套丰富的工具和组件,帮助开发者快速构建响应式和移动设备优先的网页。在本文中,我们将重点探讨 Bootstrap 4 中的多媒体对象(Media Object)组件,这是一种用于构建复杂和灵活布局的强大…...

Springmvc Thymeleaf 标签
Thymeleaf是一个适用于Java的模板引擎,它允许开发者将动态内容嵌入到HTML页面中。在SpringMVC框架中,Thymeleaf可以作为一个视图解析器,使得开发者能够轻松地创建动态网页。以下是关于SpringMVC中Thymeleaf标签的详细介绍: 一、T…...

用java来编写web界面
一、ssm框架整体目录架构 二、编写后端代码 1、编写实体层代码 实体层代码就是你的对象 entity package com.cv.entity;public class Apple {private Integer id;private String name;private Integer quantity;private Integer price;private Integer categoryId;public…...

如何利用Fiddler进行抓包并自动化
首先一般使用Fiddler都是对手机模拟器进行抓包 接下来以MUMU模拟器为例 首先打开Fiddler-->tool-->options-->connection 将要打上的勾都打上,可以看到代理的端口是8888 打开HTTPS选项 把要打的勾打上,这样子才可以接收到HTTPS的包 MUMU打开…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

热门Chrome扩展程序存在明文传输风险,用户隐私安全受威胁
赛门铁克威胁猎手团队最新报告披露,数款拥有数百万活跃用户的Chrome扩展程序正在通过未加密的HTTP连接静默泄露用户敏感数据,严重威胁用户隐私安全。 知名扩展程序存在明文传输风险 尽管宣称提供安全浏览、数据分析或便捷界面等功能,但SEMR…...

Matlab实现任意伪彩色图像可视化显示
Matlab实现任意伪彩色图像可视化显示 1、灰度原始图像2、RGB彩色原始图像 在科研研究中,如何展示好看的实验结果图像非常重要!!! 1、灰度原始图像 灰度图像每个像素点只有一个数值,代表该点的亮度(或…...
EasyRTC音视频实时通话功能在WebRTC与智能硬件整合中的应用与优势
一、WebRTC与智能硬件整合趋势 随着物联网和实时通信需求的爆发式增长,WebRTC作为开源实时通信技术,为浏览器与移动应用提供免插件的音视频通信能力,在智能硬件领域的融合应用已成必然趋势。智能硬件不再局限于单一功能,对实时…...

