【动态规划】子数组系列(上)


1. 最大子数组和
53. 最大子数组和

状态表示:以 i 位置为结尾时的所有子数组中的最大和
状态转移方程:
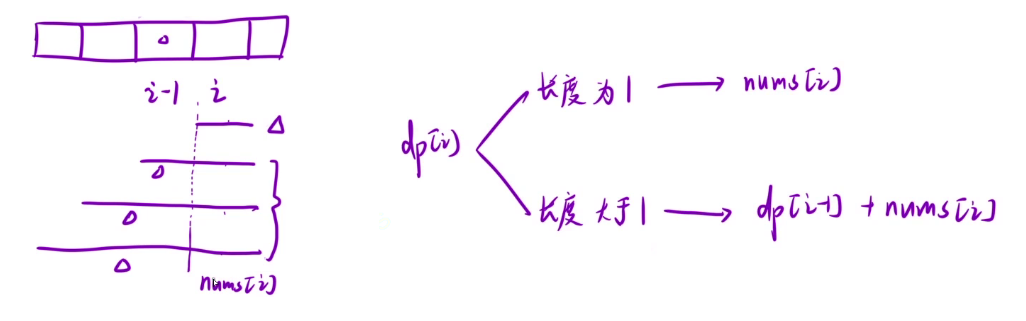
i 位置为结尾的子数组又可以分为长度为 1 的和大于 1 的,长度为 1 就是 nums[i] ,长度不为 1 就是 dp[i - 1] + nums[i],最后取这两个的最大值即可
初始化:可以多开一个元素,为了不影响后续的值默认为 0 即可,也可以单独对 dp[0] 进行初始化,就不用多开一个元素了
填表顺序:从左到右
返回值:整个 dp 表中的最大值,因为结果可能是以任意位置结尾的,如果多开一个元素的话最后取最大值就不能再带上这个值了
class Solution {public int maxSubArray(int[] nums) {int n = nums.length;int[] dp = new int[n + 1];//dp[0] = Math.max(0,nums[0]);int res = -0x3f3f3f;for(int i = 1;i <= n;i++){dp[i] = Math.max(nums[i - 1],dp[i - 1] + nums[i - 1]); res = Math.max(res,dp[i]);}return res;}
}2. 环形子数组的最大和
918. 环形子数组的最大和
这道题和上道题不同的就是是一个环形结构,首尾可以相连,这就会有下面两种情况
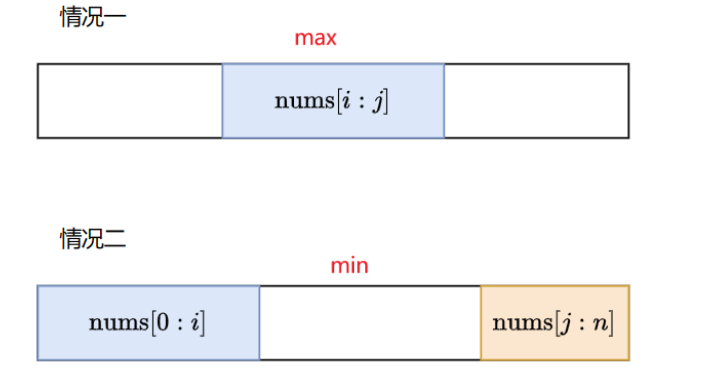
情况一和上一题是一样的,就是正常的求最大的子序列和,情况二就是首尾相连的情况,可以转化为求中间部分最小的子序列和,再用总的数组和减去这部分最小的子序列和就是最大子序列和,这两种情况求最大值就可以了
状态表示和状态转移方程都和上一题是类似的
初始化:求最大子序列和时还是 dp[0] 初始化为 0,不过求最小子序列就不一样了
dp[i] = Math.min(nums[i - 1],dp[i - 1] + nums[i - 1]);
求 dp[1] 时需要让最后的结果等于 num[0],所以 dp[i - 1] 就需要设为 0 或者一个很大的数,不过不能设为 int 的最大值,不然可能会溢出
返回值:返回两种情况的最大值,不过有一种情况需要注意,当数组中全是负数的话,第一种情况求的就是负数,第二种情况求的最小值就是整个数组和,再用数组和减去这个最小值就是 0 ,代表什么都不选,肯定是比第一种情况大的,这个时候还是需要返回第一种情况的值
class Solution {public int maxSubarraySumCircular(int[] nums) {int n = nums.length;int[] dp = new int[n + 1];int ret1 = Integer.MIN_VALUE;int sum = 0;for(int i = 1;i <= n;i++){dp[i] = Math.max(nums[i - 1],dp[i - 1] + nums[i - 1]);ret1 = Math.max(ret1,dp[i]);sum += nums[i - 1];}int ret2 = Integer.MAX_VALUE;dp[0] = 0x3f3f3f;for(int i = 1;i <= n;i++){dp[i] = Math.min(nums[i - 1],dp[i - 1] + nums[i - 1]);ret2 = Math.min(ret2,dp[i]);}if(sum == ret2) return ret1;return Math.max(ret1,sum - ret2);}
}3. 乘积最大子数组
152. 乘积最大子数组

这道题求的是乘积最大的子数组,由于是乘法,就意味着两个负数乘完之后也会变成整数
状态表示:先定义为以 i 位置为结尾时的所有子数组中的最大乘积发现,如果是负数的话也可以乘进来,所以可以定义两个状态
以 i 位置为结尾时的所有子数组中的最大乘积
以 i 位置为结尾时的所有子数组中的最小乘积
状态转移方程:
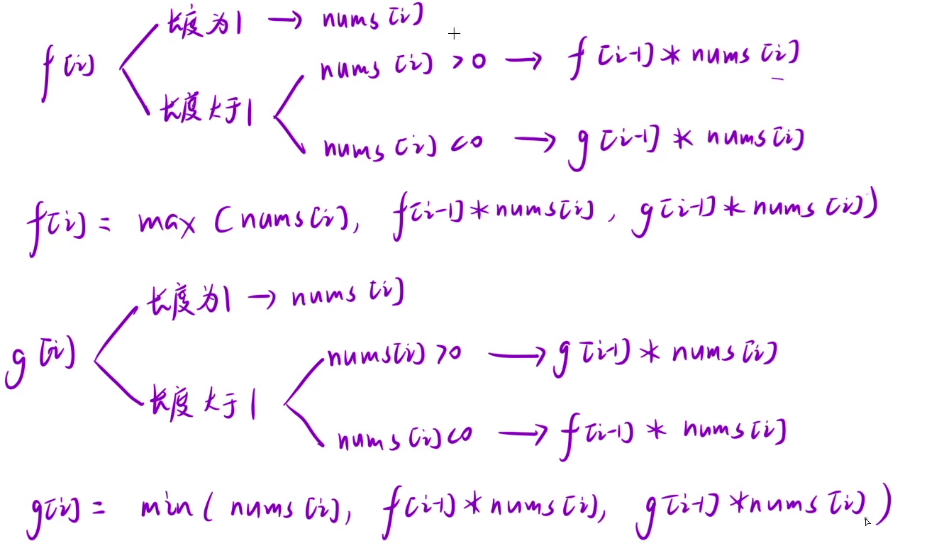
求 f[i] 时,如果说当前元素是一个负数,那么就需要乘上一个最小的负数,也就是 g[i - 1],如果是正数的话正常求前一个状态的最大值再乘当前元素就行,最终确定最大值时需要再加上当前元素,这三个数一起求一个最大值即可
同理,求最小值 g[i] 时,如果说当前元素是一个正数,那么就需要乘上一个最小的负数,也就是 g[i - 1],如果是负数的话就需要找一个最大的正数来乘,最终确定最小值时需要再加上当前元素,这三个数一起求一个最小值即可
初始化:把 f[0] 和 g[0] 设置为 1 就不影响后续的乘积赋值
填表顺序:从左到右
返回值:f 表中的最大值
class Solution {public int maxProduct(int[] nums) {int n = nums.length;int[] f = new int[n + 1];int[] g = new int[n + 1];f[0] = 1;g[0] = 1;int ret = Integer.MIN_VALUE;for(int i = 1;i <= n;i++ ){f[i] = Math.max(Math.max(nums[i - 1], f[i - 1] * nums[i - 1]), g[i - 1] * nums[i - 1]);g[i] = Math.min(Math.min(nums[i - 1], f[i - 1] * nums[i - 1]), g[i - 1] * nums[i - 1]);ret = Math.max(ret,f[i]);}return ret;}
}4. 乘积为正数的最长子数组长度
1567. 乘积为正数的最长子数组长度
状态表示:
f[i]:以 i 位置为结尾的所有子数组中乘积为正数的最长长度
g[i]:以 i 位置为结尾的所有子数组中乘积为负数的最长长度
状态转移方程:
还是和之前一样,可以分为长度为 1 的和长度大于 1 的,当长度为 1 时又可以分为 nums[i] 是正数还是负数两种情况,当是正数时长度就是 1,负数时就是 0,再看长度大于 1 的,也可以分为 nums[i] 是正数还是负数两种情况,当 num[i] 是正数时,就是从以 i - 1 为结尾时数组中的乘积为正数的最长长度加 1 即可,也就是 f[i - 1] + 1,当 num[i] 是负数时,就需要在 i - 1 为结尾时数组中的乘积为负数的长度加上 1,所以需要再定义一个 g[i] 状态数组来表示,也就是 g[i - 1] + 1,但是如果之前找不到一个以 i - 1 为结尾的数组,那么 g[i - 1] 就是 0,此时就不能继续加 1,因为 num[i] 是负数,这个长度不能加
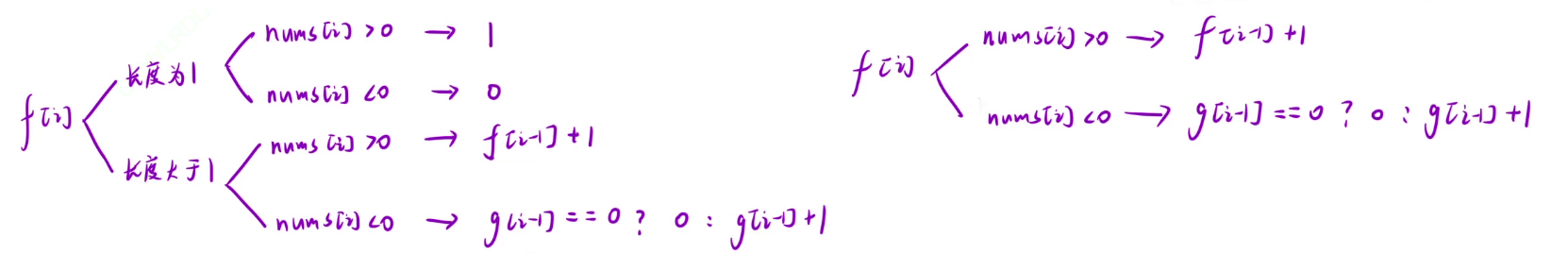
为了简便,长度为 1 时的状态可以和下面长度大于 1 的合并一下,不影响结果
接下来看 g[i] 的状态转移方程:同理,也可以分为长度为 1 和长度大于 1 两种情况,接着二者又可以分为 num[i] 大于 0 和小于 0 两种情况,当 num[i] 大于 0 时,需要找到 i - 1 为结尾的乘积为负数的最长长度,也就是 g[i - 1],然后加 1,这里还是一样的,如果没有找到,那么 g[i - 1] 就是 0,num[i] 为正数,要求的是负数,所以这个 1 需要判断一下才能加,num[i] 小于 0 时,就需要找一个 i - 1 为结尾的乘积为正数的最长长度,也就是 f[i - 1] 再加 1,这时就不需要判断,找不到也没关系,可以直接 + 1
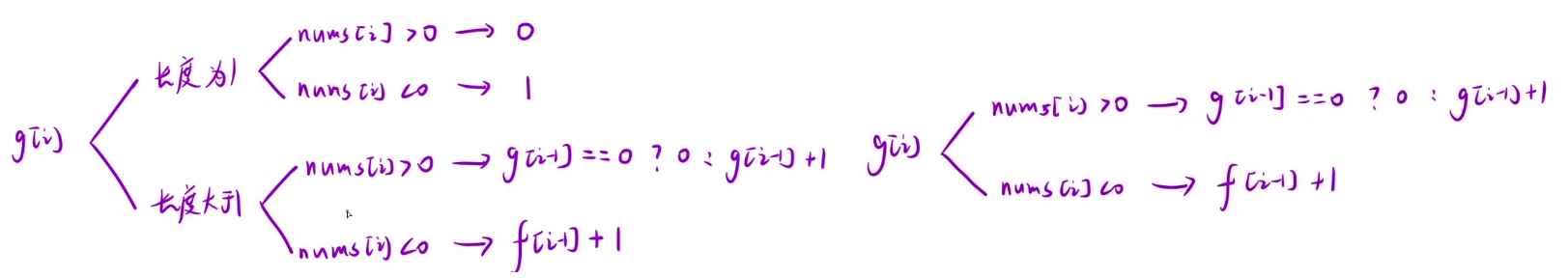
长度为 1 时也可以合并一下,不影响结果
nums[i] 等于 0 的情况直接不考虑就行
初始化:如果 nums[0] 是大于 0 的话,g[1] 应该是 0,也就是 g[0] = 0即可, 如果是小于 0 的话 g[1] 应该是 1,也就是 f[0] 应该是 0
填表顺序:从左到右,两个表一起填
返回值:f 表中的最大值
class Solution {public int getMaxLen(int[] nums) {int n = nums.length;int[] f = new int[n + 1];int[] g = new int[n + 1];int ret = 0;for(int i = 1;i <= n;i++){if(nums[i - 1] > 0){f[i] = f[i - 1] + 1;g[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1;}else if(nums[i - 1] < 0){f[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1;g[i] = f[i - 1] + 1;}ret = Math.max(f[i],ret);}return ret;}
}
相关文章:

【动态规划】子数组系列(上)
1. 最大子数组和 53. 最大子数组和 状态表示:以 i 位置为结尾时的所有子数组中的最大和 状态转移方程: i 位置为结尾的子数组又可以分为长度为 1 的和大于 1 的,长度为 1 就是 nums[i] ,长度不为 1 就是 dp[i - 1] nums[i]&…...

字节青训营入门算法题:飞行棋分组
链接:飞行棋分组🔗🔗 题目 现在有一堆飞行棋棋子,每个棋子上标有数字序号。需要将这些棋子分成若干组,每组包含5个棋子,且组内所有棋子的数字序号必须相同。需要判断是否可以完成这样的分组。 解答 为了…...

# 执行 rpm -qa | grep qq 查询软件安装情况时报错 数据库损坏 db3 error(-30974)
执行 rpm -qa | grep qq 查询软件安装情况时报错 数据库损坏 db3 error(-30974) 一、问题描述: 在 linux 系统上,使用包管理工具 rpm 查询某一个软件安装情况,如:执行 rpm -qa | grep qq 时,报错 数据库损坏 db3 err…...

离线服务器上复现G3SR论文实验
代码地址:https://github.com/AllminerLab/Code-for-G3SR-master 论文地址:https://ieeexplore.ieee.org/abstract/document/9741079/ 因为直接按照作者的方法操作会出现问题,故笔者在这里记录一下的实验过程。 实验环境 python=3.6 pytorch pytorch的下载命令需要自行前往…...

Android 未来可能支持 Linux 应用,Linux 终端可能登陆 Android 平台
近日,根据 android authority 的消息,Google 正在开发适用于 Android 的 Linux 终端应用,而终端应用可以通过开发人员选项启用,并将 Debian 安装在虚拟机中。 在几周前,Google 的工程师开始为 Android 开发新的 Termi…...

PostgreSQL学习笔记十四:PL/Python自定义函数
在 PostgreSQL 中可以使用 PL/Python 语言来创建自定义函数。以下是一个示例步骤: 一、创建自定义函数 连接到 PostgreSQL 数据库,可以使用 psql 命令行工具或者通过数据库管理工具。 执行以下 SQL 语句创建一个简单的 PL/Python 函数: C…...

计算机毕业设计 | springboot商城售后管理系统 购物平台(附源码)
1,绪论 1.1 开发背景 在数字化时代的推动下,产品售后服务管理机构面临着信息化和网络化的挑战。传统的手工管理和纸质档案已经无法满足管理人员和读者的需求。为了提高产品售后服务管理机构的管理效率和服务质量,开发和实现一个基于Java的售…...

(全网独家)面试要懂运维真实案例:HDFS重新平衡(HDFS Balancer)没触发问题排查
在面试时,面试官为了考察面试者是否真的有经验,经常会问运维集群时遇到什么问题,解决具体流程。下面是自己遇到HDFS Balancer没执行,花了半天时间进行排查,全网独家的案例和解决方案。 目录 使用CDH自带重新平衡操作…...

【数据结构笔记】搜索树
二叉搜索树 任一节点x的左/右子树中,所有非空节点均不大于(不小于)x 必须是所有的非空节点,仅左右孩子不够(左孩子的右孩子可能很大)一棵二叉树是二叉搜索树当且仅当中序遍历序列是单调非降序列 两棵二叉…...

如何使用UART(STM32 HAL库)
UART (通用异步收发器)是在 USART (通用同步异步收发器)基础上裁剪掉了同步通信功能,只剩下异步通信功能。关于通信和串口的基本知识,可参见文章《串口通信简介-CSDN博客》和《数据通信的一些基础概念-CSDN…...

星巴克英语
用流利的英文点星巴克 一杯咖啡 英文中文英文中文barista咖啡师coffee maker家用咖啡机cup sleeve杯套coffee stirrer咖啡棒coffee cup lid咖啡杯盖子straw吸管latte art咖啡拉花for here内用to go外带 例句: Could I have a cup sleeve for my coffee , please…...

权重衰减与暂退法——paddle部分
权重衰减与暂退法——paddle部分 本文部分为paddle框架以及部分理论分析,torch框架对应代码可见权重衰减与暂退法torch import paddle print("paddle version:",paddle.__version__)paddle version: 2.6.1当我们谈论机器学习模型的性能时,经…...

golang获取当天最小的时间,以DateTime的string格式返回
推荐学习文档 golang应用级os框架,欢迎stargolang应用级os框架使用案例,欢迎star案例:基于golang开发的一款超有个性的旅游计划app经历golang实战大纲golang优秀开发常用开源库汇总想学习更多golang知识,这里有免费的golang学习笔…...

2025 - 中医学基础 - 考研 - 职称
2025 - 中医学基础 - 考研 - 职称 第1章 中医学导论 1.中医学的指导思想是()( ) [单选] A.阴阳学说 B.五行学说 C.精气学说 D.整体观念 E.辨证论治 正确答案: D 2.中医学的理论核心是&…...

Pandas库
一、安装 Pandas是一个基于Python构建的专门进行数据操作和分析的开源软件库,它提供了高效的数据结构和丰富的数据操作工具。 安装 pip install pandas 二、核心数据结构 Pandas库中最常用的数据类型是Series和DataFrame: Series:一维数…...

Qt网络编程: 构建高效的HTTP文件下载器
文章目录 注意事项调用示例在使用Qt进行HTTP下载时,通常会使用QNetworkAccessManager类来管理HTTP请求和响应。这个类提供了进行网络请求的能力,包括下载文件。下面是使用Qt进行HTTP下载的一个示例,以及在实现时应考虑的一些注意事项。 注意事项 1.错误处理 始终检查QNetwo…...

Python 将Word, Excel, PDF和PPT文档转换为OFD格式
目录 使用工具 Python 将Word文档转换为OFD Python 将Excel文档转换为OFD Python 将PDF文档转换为OFD Python 将PPT文档转换为OFD OFD(Open Fixed-layout Document)是中国国家标准的电子文档格式,主要用于政府、金融等行业的正式文档传输…...
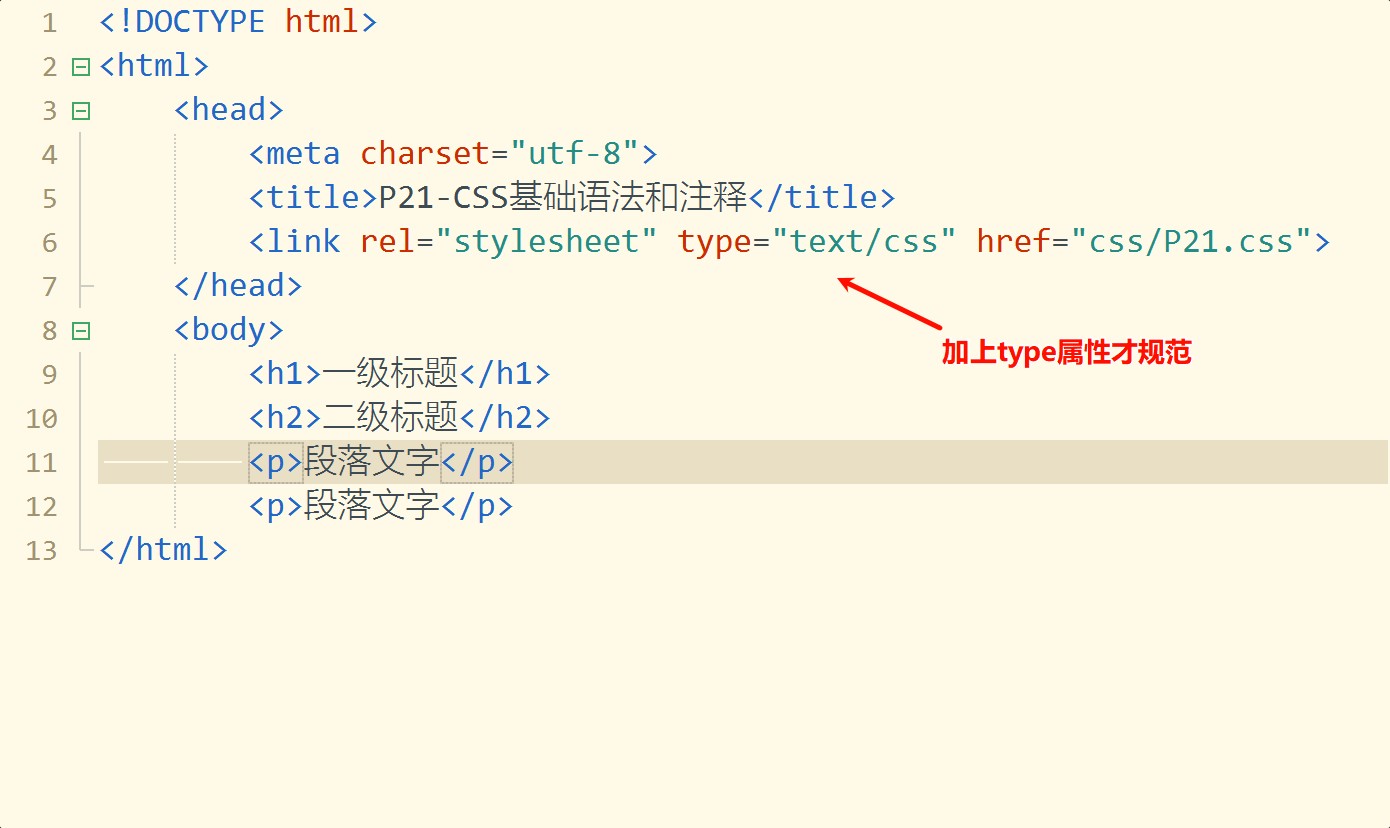
QD1-P21-P22 CSS 基础语法、注释、使用方法
本节学习:CSS 基础语法和注释,以及如何使用CSS定义的样式。 本节视频 https://www.bilibili.com/video/BV1n64y1U7oj?p21 CSS 基本语法 CSS(层叠样式表)的基本语法相对简单,由选择器和一组包含在花括号 {} 中的声…...

您是否也在寻找免费的 PDF 编辑器工具?10个备选PDF 编辑器工具
您是否也在寻找免费的 PDF 编辑器工具? 如果是,那么您在互联网上处于最佳位置! 本指南中提到的所有 10 大免费 PDF 编辑器工具都易于使用,可以允许您添加文本、更改图像、添加图形、填写表格、添加签名等等。 因此,…...
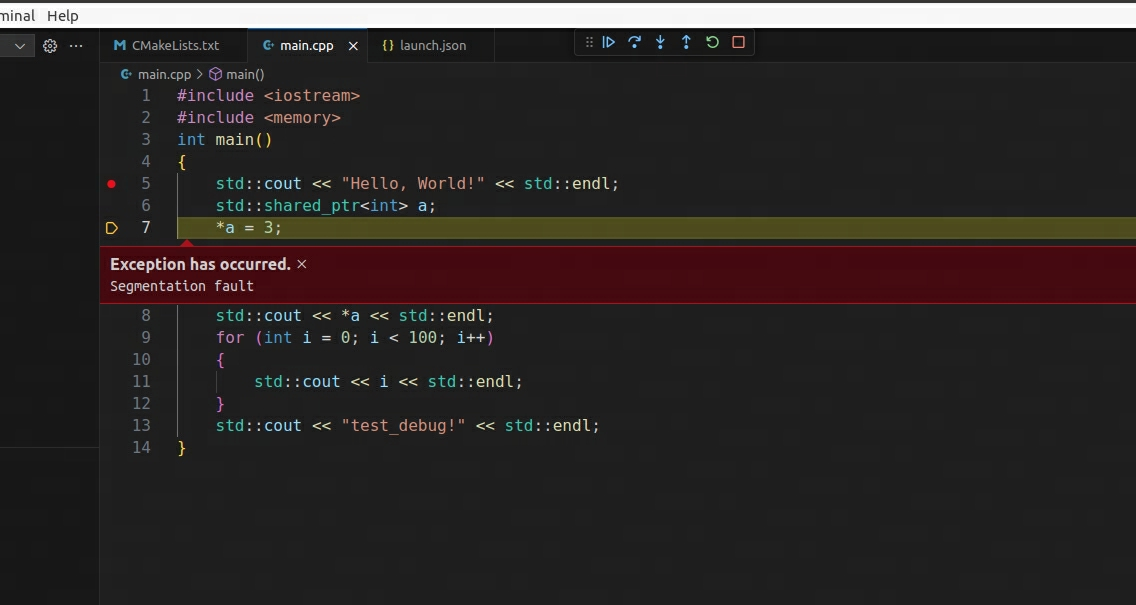
C++调试方法(Vscode)(一) ——本地调试
初学者在调试一段代码的时候,经常出于不明原因,写出bug,导致程序崩溃。但是定位崩溃的地方时,往往采用简单而朴素的方法:即采用cout或者printf进行输出。这种方式既原始,又低效。一个合格的工程师应该是通过…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

游戏开发中常见的战斗数值英文缩写对照表
游戏开发中常见的战斗数值英文缩写对照表 基础属性(Basic Attributes) 缩写英文全称中文释义常见使用场景HPHit Points / Health Points生命值角色生存状态MPMana Points / Magic Points魔法值技能释放资源SPStamina Points体力值动作消耗资源APAction…...

Selenium 查找页面元素的方式
Selenium 查找页面元素的方式 Selenium 提供了多种方法来查找网页中的元素,以下是主要的定位方式: 基本定位方式 通过ID定位 driver.find_element(By.ID, "element_id")通过Name定位 driver.find_element(By.NAME, "element_name"…...

