多元线性回归:机器学习中的经典模型探讨
引言
多元线性回归是统计学和机器学习中广泛应用的一种回归分析方法。它通过分析多个自变量与因变量之间的关系,帮助我们理解和预测数据的行为。本文将深入探讨多元线性回归的理论背景、数学原理、模型构建、技术细节及其实际应用。
一、多元线性回归的背景与发展
1.1 回归分析的定义
回归分析是一种统计技术,用于建模和分析变量之间的关系。多元线性回归是回归分析的一种扩展形式,它考虑多个自变量对因变量的影响。具体来说,它试图找出一个线性方程来描述因变量与多个自变量之间的关系。

1.2 多元线性回归的发展
多元线性回归的研究历史悠久,可以追溯到20世纪初。随着统计学和计算机科学的发展,特别是计算能力的提升,基于最小二乘法的多元线性回归逐渐成为主流方法。近年来,随着机器学习的兴起,多元线性回归被广泛应用于各种数据分析任务,并与其他机器学习模型相结合,成为数据科学中的重要工具。
下表展示了多元线性回归的发展历程:
| 年代 | 技术 | 代表模型 |
|---|---|---|
| 20世纪初 | 经典统计学 | 多元线性回归模型 |
| 20世纪中叶 | 计算机科学兴起 | 多元回归分析 |
| 21世纪 | 机器学习方法 | 结合正则化的多元回归 |
二、多元线性回归的核心理论
2.1 模型定义
多元线性回归模型的数学表达式为:
![]()
- y:因变量
- β0:截距
- β1,β2,...,βn:自变量的系数
- x1,x2,...,xn:自变量
- ϵ:误差项
2.2 最小二乘法
最小二乘法是求解多元线性回归模型参数的常用方法。其基本思想是通过最小化预测值与真实值之间的平方差来找到最佳拟合线。最小化的目标函数为:


2.3 假设检验与模型评估
在多元线性回归中,假设检验用于检验各个自变量的显著性。常用的检验方法包括t检验和F检验。模型评估则主要通过决定系数(R2R^2R2)来衡量模型的拟合优度。R2R^2R2的值介于0到1之间,越接近1表示模型越好地解释了因变量的变异。
三、多元线性回归的实现
3.1 数据准备
首先,我们需要准备数据集。通常,一个数据集应该包含多个特征以及对应的目标变量。我们将使用pandas库来处理数据。
3.2 实现代码
在Python中,可以使用scikit-learn库来实现多元线性回归模型。下面是一个详细的示例代码:
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score# 生成示例数据
np.random.seed(42) # 设置随机种子
data = {'Feature1': np.random.rand(100),'Feature2': np.random.rand(100),'Feature3': np.random.rand(100),'Target': np.random.rand(100) * 100
}
df = pd.DataFrame(data)# 划分训练集和测试集
X = df[['Feature1', 'Feature2', 'Feature3']]
y = df['Target']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 创建多元线性回归模型
model = LinearRegression()
model.fit(X_train, y_train)# 进行预测
y_pred = model.predict(X_test)# 评估模型
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)print(f'Mean Squared Error: {mse:.2f}')
print(f'R² Score: {r2:.2f}')
在这段代码中,我们生成了一些随机数据,创建了一个多元线性回归模型,并评估了其性能。具体步骤如下:
- 数据生成:随机生成特征和目标变量。
- 数据划分:使用
train_test_split将数据分为训练集和测试集。 - 模型训练:使用
LinearRegression类创建模型并训练。 - 预测与评估:进行预测,并使用均方误差和决定系数评估模型性能。
四、多元线性回归的实际应用
4.1 房价预测
多元线性回归在房地产行业中应用广泛。通过考虑面积、卧室数量、地理位置等因素,可以预测房价。这为购房者和投资者提供了重要的决策依据。
应用示例
在一个房价预测模型中,我们可能使用以下特征:
- 房屋面积
- 卧室数量
- 卫生间数量
- 地理位置(可能转化为数值)
4.2 销售预测
在市场营销中,多元线性回归可以帮助企业分析广告支出、市场活动、季节因素等对销售额的影响,从而优化营销策略。
应用示例
销售预测模型可以考虑的特征包括:
- 广告预算
- 产品价格
- 竞争对手活动
4.3 医疗研究
在医疗健康领域,多元线性回归可用于分析各种因素(如年龄、体重、生活习惯等)对疾病发生的影响,为公共健康决策提供依据。
应用示例
可以构建一个模型来分析:
- 年龄
- BMI(身体质量指数)
- 吸烟状态
- 锻炼频率
五、多元线性回归的挑战与未来
5.1 多重共线性
在多元线性回归中,自变量之间存在较强的相关性(多重共线性)时,可能导致模型的不稳定性和解释性降低。可以通过计算自变量的方差膨胀因子(VIF)来检测多重共线性。如果VIF值大于5或10,说明可能存在多重共线性问题。
5.2 过拟合
过拟合是多元线性回归中的常见问题,尤其是在自变量较多时。使用交叉验证和正则化(如岭回归、套索回归)可以有效降低过拟合的风险。
5.3 未来的发展方向
未来,多元线性回归可能会向以下方向发展:
- 模型压缩与高效推理:研究如何压缩模型,使其在设备端也可以运行,从而实现低延迟的应用。
- 跨模态学习:结合视觉、音频等模态,语言模型可以更好地理解和生成多模态内容。
- 自监督学习:通过自监督学习,模型能够更有效地利用无标注数据,降低数据标注成本。
六、结论
多元线性回归作为一种经典的机器学习模型,在数据分析和预测中仍然发挥着重要作用。通过理解其基本原理、实现方法和实际应用,读者可以更有效地运用这一技术解决实际问题。虽然面临着一些挑战,但通过适当的技术手段和方法,我们仍然可以充分发挥多元线性回归的潜力。
希望通过本篇博客,读者能够对多元线性回归有更深入的理解,并能够在各类实际问题中灵活运用这一模型。无论是数据科学家还是研究人员,掌握多元线性回归都将为你的职业发展和科研工作带来巨大的推动力。
相关文章:

多元线性回归:机器学习中的经典模型探讨
引言 多元线性回归是统计学和机器学习中广泛应用的一种回归分析方法。它通过分析多个自变量与因变量之间的关系,帮助我们理解和预测数据的行为。本文将深入探讨多元线性回归的理论背景、数学原理、模型构建、技术细节及其实际应用。 一、多元线性回归的背景与发展…...

域1:安全与风险管理 第1章实现安全治理的原则和策略
---包括OSG 1、2、3、4 章--- 第1章、实现安全治理的原则和策略 1、由保密性、完整性和可用性组成的 CIA 三元组。 保密性原则是指客体不会被泄露给 未经授权的主体。完整性原则是指客体保持真实性且只被经过授权的主体进行有目的的修改。 可用性原则指被授权的主体能实时和…...

【大数据】学习大数据开发应该从哪些技术栈开始学习?
学习大数据开发可以从以下几个技术栈和阶段入手。以下内容按学习顺序和重要性列出,帮助你逐步掌握大数据开发的核心技能: 1. 编程基础 Java:Hadoop 和许多大数据工具(如 Spark、Flink)的核心代码都是用 Java 编写的&…...

CentOS快速配置网络Docker快速部署
CentOS快速配置网络&&Docker快速部署 CentOS裸机Docker部署1.联通外网2.配置CentOS镜像源3.安装Docker4.启动Docker5.CentOS7安装DockerCompose Bug合集ERROR [internal] load metadata for docker.io/library/java:8-alpineError: Could not find or load main class …...

Grounded-SAM Demo部署搭建
目录 1 环境部署 2 Grounded-SAM Demo安装 3 运行Demo 3.1 运行Gradio APP 3.2 Gradio APP操作 1 环境部署 由于SAM建议使用CUDA 11.3及以上版本,这里使用CUDA 11.4版本。 另外,由于整个SAM使用的是Pytorch开发,因此需要Python环境&…...
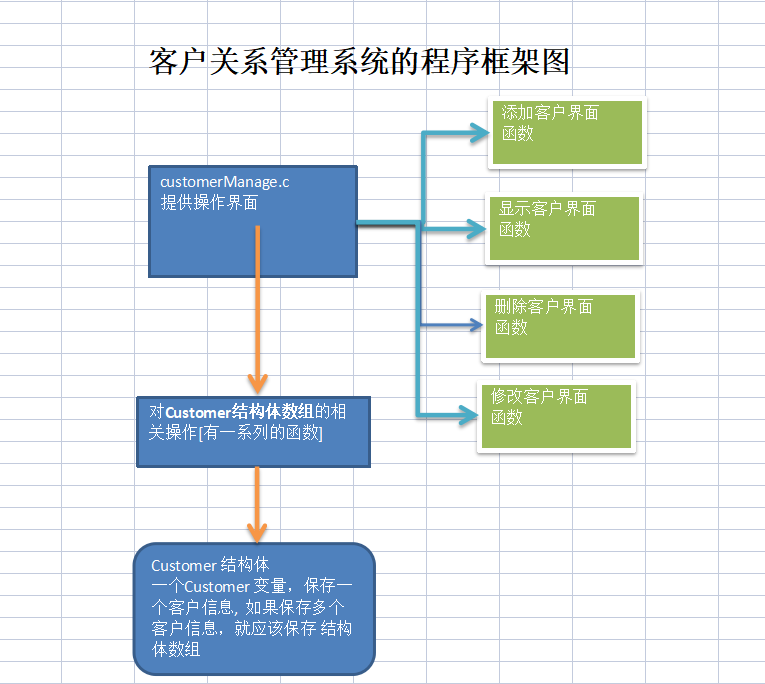
C语言 | 第十六章 | 共用体 家庭收支软件-1
P 151 结构体定义三种形式 2023/3/15 一、创建结构体和结构体变量 方式1-先定义结构体,然后再创建结构体变量。 struct Stu{ char *name; //姓名 int num; //学号 int age; //年龄 char group; //所在学习小组 float score; //成绩 }; struct Stu stu1, stu2; //…...

【论文阅读】Learning a Few-shot Embedding Model with Contrastive Learning
使用对比学习来学习小样本嵌入模型 引用:Liu, Chen, et al. “Learning a few-shot embedding model with contrastive learning.” Proceedings of the AAAI conference on artificial intelligence. Vol. 35. No. 10. 2021. 论文地址:下载地址 论文代码…...

OKHTTP 如何处理请求超时和重连机制
😄作者简介: 小曾同学.com,一个致力于测试开发的博主⛽️,主要职责:测试开发、CI/CD 如果文章知识点有错误的地方,还请大家指正,让我们一起学习,一起进步。 😊 座右铭:不…...

基于Springboot vue的流浪狗领养管理系统设计与实现
博主介绍:专注于Java(springboot ssm 等开发框架) vue .net php python(flask Django) 小程序 等诸多技术领域和毕业项目实战、企业信息化系统建设,从业十五余年开发设计教学工作☆☆☆ 精彩专栏推荐订阅☆☆☆☆☆不然下次找…...

爬虫案例——网易新闻数据的爬取
案例需求: 1.爬取该新闻网站——(网易新闻)的数据,包括标题和链接 2.爬取所有数据(翻页参数) 3.利用jsonpath解析数据 分析: 该网站属于异步加载网站——直接网页中拿不到,需要…...

SpringCloud 2023 Gateway的Filter配置介绍、类型、内置过滤器、自定义全局和单一内置过滤器
目录 1. Filter介绍2. Filter类型3. 内置过滤器3.1 请求头(RequestHeader)相关GatewayFilter Factory3.2 请求参数(RequestParameter)相关GatewayFilter Factory3.3 回应头(ResponseHeader)相关GatewayFilter Factory3.4 前缀和路径相关GatewayFilter Factory3.5 Default Filte…...

从银幕到现实:擎天柱机器人即将改变我们的生活
擎天柱(Optimus)是《变形金刚》系列电影中的主角,如今也成为特斯拉正在开发的通用机器人。2022年10月,特斯拉展示了这一机器人的初始版本,创始人埃隆马斯克表示,希望到2023年能够启动生产。他指出ÿ…...

408算法题leetcode--第33天
509. 斐波那契数 题目地址:509. 斐波那契数 - 力扣(LeetCode) 题解思路:dp 时间复杂度:O(n) 空间复杂度:O(n) 代码: class Solution { public:int fib(int n) {// dp数组含义:dp[i]即i位置…...

OCR模型调研及详细安装
OCR模型调研及详细安装 1 搭建 Tesseract-OCR 环境。 1.1 注意需先手动安装Tesseract-OCR, 下载地址:https://digi.bib.uni-mannheim.de/tesseract/?CM;OD 注意:安装的时候选中中文包(安装时把所有选项都勾上)。 安装磁盘选择…...

C++第六讲:STL--vector的使用及模拟实现
C第六讲:STL--vector的使用及模拟实现 1.vector简介2.vector的常见接口介绍2.1constructor -- 构造2.2destructor -- 析构2.3begin、end2.3.1vector和string的区别、vector<string> 2.4rbegin、rend2.5cbegin、cend2.6crbegin、crend2.7size、max_size、resiz…...

2024年字节抖音前端面经,这次问的很基础!
文章同步在公众号:萌萌哒草头将军,欢迎关注!!! 一面 es6新特性有哪些 新增了let、const关键字替换var声明变量,因为var会导致变量提升,在申明之前可以访问变量。新增了箭头函数,新…...

vscode提交修改Failed to connect to github.com port 443: Timed out
参考内容:timed out 只需3步:设置代理、取消代理、再次提交。👉 2.1 设置代理 $ git config --global https.proxy 1 👉 2.2 取消代理 $ git config --global --unset https.proxy 1之后关闭bash,再去vscode里面pull …...

通过docker镜像安装elasticsearch和kibana
目录 前言安装elasticsearch:7.17.21安装对应版本的kibana 前言 本文主要参考:https://blog.csdn.net/qq_23859799/article/details/138521052,内容基本一致,改动了部分错误 安装elasticsearch:7.17.21 拉取镜像:docker pull d…...

seaCMS v12.9代码审计学习(下半)
文章目录 admin/admin_safe.php任意文件下载CSRF 添加管理员账户CSRF配合XSS弹cookie admin/admin_safe.php任意文件下载 在admin_safe.php文件下有着这么一段代码,他的作用时检查action的值是否为download,如果为download那么将你传入的文件直接打印给…...

麒麟信安CentOS安全加固案例获评中国信通院第三届“鼎新杯”数字化转型应用奖
“鼎新杯”数字化转型应用大赛,由中国通信标准化协会主办、中国信息通信研究院承办,以落实国家“十四五”规划关于“加快数字化发展,建设数字中国”的总体要求为目标,意在打造一批具有产业引领与推广应用效应的企业数字化转型应用…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...
