MRSO算法(JCR2区)
原论文摘要:智能技术的快速发展促使利用自然行为来解决复杂问题的优化算法得以发展。其中,鼠群优化算法(Rat Swarm Optimizer,RSO)受老鼠的社会和行为特征启发,在各个领域已展现出潜力,但其收敛精度和探索能力有限。为解决这些缺点,本研究引入改进的鼠群优化算法(Modified Rat Swarm Optimizer,MRSO),旨在增强探索与开发之间的平衡。MRSO 进行了独特的改进以提高搜索效率和鲁棒性,使其适用于诸如焊接梁、压力容器和齿轮传动设计等具有挑战性的工程问题。通过经典基准函数的广泛测试表明,MRSO 显著提高了性能,在九种多模态函数中的六种以及所有七种固定维度多模态函数中避免了局部最优并实现了更高的精度。在 CEC 2019 基准测试中,MRSO 在十项函数中的六项中优于标准 RSO,展示出卓越的全局搜索能力。当应用于工程设计问题时,MRSO 始终比 RSO 提供更好的平均结果,证明了其有效性。此外,我们使用经典和 CEC-2019 基准将我们的方法与八种近期知名算法进行了比较。MRSO 在 23 个经典基准函数中的六种以及 CEC-2019 基准函数中的四种中优于这些算法中的每一种,这些结果进一步证明了 MRSO 作为工程应用中可靠且高效的优化工具的重大贡献。
function [output] = MRSO(itt,F)for n=1:ittFunction_name=F; % Name of the test function from beanchmark test functions[lb,ub,dim,fobj]=CEC2019(Function_name);ShowIterInfo = true; % Flag for Showing Iteration Information MaxIt = 500; % max Iteration numbersnPop = 30; % Population sizePosition=zeros(1,dim);Score=inf; Positions=init(nPop,dim,ub,lb); %initializationConvergence=zeros(1,MaxIt);l=0; %% Parameters of MRSOx = 1;y = 5;R = floor((y-x).*rand(1,1) + x); % equation No. (3)for it=1:MaxIt
% for i=1:size(Positions,1) Flag4Upper_bound=Positions(i,:)>ub;Flag4Lower_bound=Positions(i,:)<lb;
Positions(i,:)=(Positions(i,:).*(~(Flag4Upper_bound+Flag4Lower_bound)))+ub.*Flag4Upper_bound+lb.*Flag4Lower_bound; fitness=fobj(Positions(i,:));if fitness<Score Score=fitness; Position=Positions(i,:);endendF1=R-l*((R)/MaxIt); % equation No. (6)F2=(1-it*((1)/MaxIt)); % equation No. (7)F3=(2*rand-1*rand); % equation No. (8) Ar=F1*F2*F3; % equation No. (9) for i=1:nPopfor j=1:dim C=2*rand(); % equation No. (4) Positions(i,j)=Position(j)-(Ar*Positions(i,j)+abs(C*((Position(j)-Positions(i,j))))); % equation No. (1)endendl=l+1; Convergence(it)=Score;% Display Iteration Informationif ShowIterInfodisp(['Iteration ' num2str(it) ': Best Cost = ' num2str(Convergence(it))]);endendout.pop = Positions;out.BestSol = Score;out.BestCosts = Convergence;semilogy(Convergence, 'LineWidth', 2);xlabel('Iteration');ylabel('Best Cost');grid on;output = zeros(itt, 1);output1 (n) = Score; % added!output = output1;end
end相关文章:
)
MRSO算法(JCR2区)
原论文摘要:智能技术的快速发展促使利用自然行为来解决复杂问题的优化算法得以发展。其中,鼠群优化算法(Rat Swarm Optimizer,RSO)受老鼠的社会和行为特征启发,在各个领域已展现出潜力,但其收敛…...

最新Spring Boot3框架入门教程,基础知识讲解(参考官方文档),同时基于MybatisPlus+MYSQL搭建后台管理系统基础流程(附源码)
本文所涉及的代码以及相关文件均上传至仓库:GitHub - yang66-hash/XDPropertyManagementSystemDemo: This is a demo template based on SpringBoot3 in the background of property management system. Spring Boot 是由 Pivotal 团队开发的一款开源框架,它可以帮助…...

导数的概念及在模型算法中的应用
一. 导数概念与计算 1. 导数的物理意义: 瞬时速率。一般的,函数yf(x)在x处的瞬时变化率是 2. 导数的几何意义: 曲线的切线,当点趋近于P时,直线 PT 与曲线相切。容易知道,割线的斜率是当点趋近于 P 时&…...

获取首日涨停封盘后第二次交易日上涨/下跌的概率
有许多投资者喜欢在股票涨停封盘后,跟进买入。普通股民会认为一个能在今日涨停封盘的股票,证明其上市公司正有十分重大的利好信息,只需要跟进购买便可以获取短期利益。 我们用数据来看一下在当日涨停封盘后,第二次交易日是上涨还…...

shell $ 用法
Shell脚本中$符号的几种用法小结_linux shell_脚本之家 Shell 传递参数 | 菜鸟教程 $ 符号说明$0Shell 的命令本身1到9表示 Shell 的第几个参数$?显示最后命令的执行情况$#传递到脚本的参数个数$$脚本运行的当前进程 ID 号$*以一个单字符串显示所有向脚本传递的参数$!后台运行…...

如何用支付宝实现靠脸吃饭
还记得上学时,每当下课铃声响起,我们就会像一群脱缰的野马一样,浩浩荡荡地冲向食堂。最令人崩溃的时刻莫过于终于到达打饭窗口前排时,却发现饭卡忘带了!但现在,这种情况将不再发生。许多学校食堂已经配备了…...
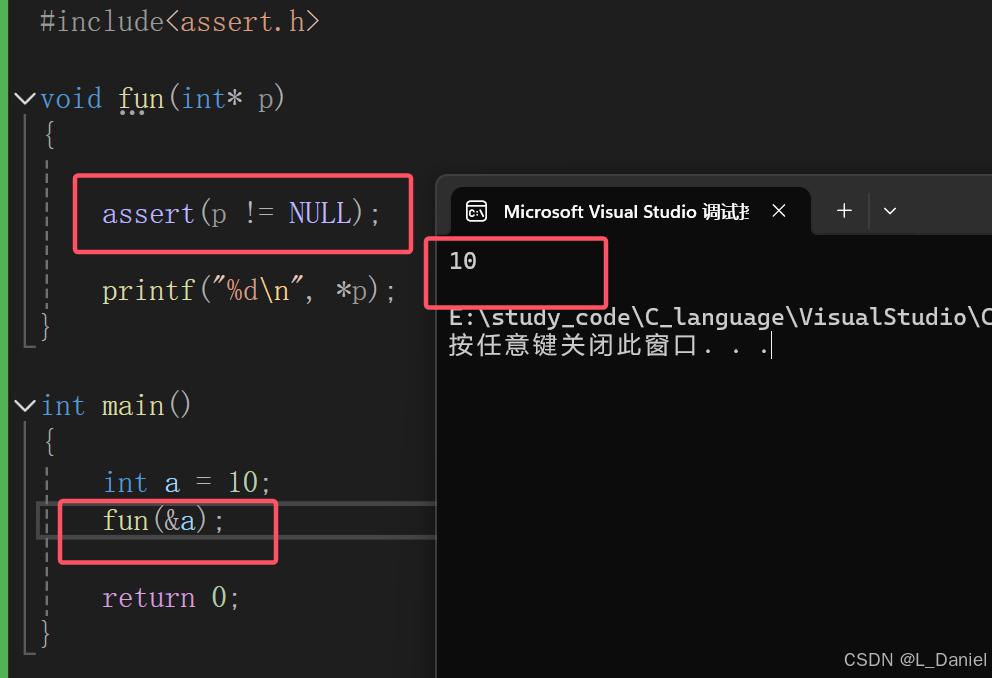
Visual Studio的实用调试技巧总结
对于很多学习编程的老铁们来说,是不是也像下面这张图一样写代码呢? 那当我们这样编写代码的时候遇到了问题?大家又是怎么排查问题的呢?是不是也像下面这张图一样,毫无目的的一遍遍尝试呢? 这篇文章我就以 V…...

graphrag学习总结
学习视频:b站链接 项目链接 GraphRAG 的基本概念 Document(文档):系统中的输入文档。这些文档要么代表CSV中的单独行,要么代表单独的txt文件。 TextUnit(文本块):要分析的文本块。…...
)
专题:贪心算法(已完结)
1.分发饼干 方法一:用最大的胃口 找到最大的饼干(先遍历胃口) class Solution { public:int findContentChildren(vector<int>& g, vector<int>& s) {// 主要思路 用最大的饼干找最大的胃口sort(g.begin(),g.end());so…...

Hadoop的三种运行模式:单机模式、伪分布式模式和完全分布式模式
单机模式 单机模式是Hadoop最简单的运行模式。在单机模式下,所有Hadoop组件都运行在单个机器上,包括HDFS、MapReduce等。由于只有一个节点参与计算,单机模式适用于开发和测试阶段,不适合用于处理大规模数据。在单机模式下…...

JavaScript将array数据下载到Excel中
具体代码如下: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta name"viewport" content"widt…...

【前端】Bootstrap:快速开始
Bootstrap 是一个功能强大且易于使用的前端框架,专门用于创建响应式和移动优先的网页。学习Bootstrap不仅可以帮助你快速构建现代网页,还可以提升你对前端开发流程的理解。本教程将从基础概念开始,逐步引导你掌握Bootstrap,并通过…...

文献阅读(222) VVQ协议死锁
题目:VVQ: Virtualizing Virtual Channel for Cost-Efficient Protocol Deadlock Avoidance时间:2023会议:HPCA研究机构:KAIST request-reply协议死锁如下图所示,每个node收到request之后发送reply,但是想…...

Node.js管理工具NVM
nvm(Node Version Manager)是一个用于管理多个 Node.js 版本的工具。以下是 nvm 的使用方法和一些常见命令: 一、安装 nvm 下载 nvm: 地址:https://github.com/coreybutler/nvm-windows/releases访问 nvm 的 GitHub 仓…...

云原生后端
云原生后端(Cloud-Native Backend)是指在云计算环境中,利用云原生技术(如容器、微服务、服务网格等)构建和部署后端应用程序的一种方法。以下是对云原生后端的详细讲解: 1. 定义 云原生是一种设计和构建应…...

充电宝哪个品牌值得买?2024年五款靠谱充电宝推荐
哪个品牌充电宝值得买?用过这么多款充电宝,个人还是觉得充电快、小巧便携的充电宝使用会更加的方便!在当今快节奏的生活中,手机已成为我们不可或缺的伙伴。然而,随着智能手机功能的日益强大,电池续航问题也…...

YOLOv11对比YOLOV8网络结构变化分析,帮助你真正的理解和学习yolo框架
本文在大佬的文章YOLOv11 | 一文带你深入理解ultralytics最新作品yolov11的创新 | 训练、推理、验证、导出 (附网络结构图)基础上做了一些补充。 一、YOLOv11和YOLOv8对比 二、YOLOv11的网络结构图 下面的图片为YOLOv11的网络结构图。 三、YOLOv11…...

弃用RestTemplate,RestClient真香!
在Spring框架的发展历程中,RestTemplate作为发起HTTP请求的同步API,曾经扮演着举足轻重的角色。然而,随着技术的不断进步和微服务架构的普及,RestTemplate的局限性逐渐显现,尤其是在处理高并发和异步请求时。因此&…...

electron-vite_10electron-updater软件更新
网很多electron-updater更新文章,这里只简单写一下演示代码; 为什么选择 electron-updater插件可以自动更新应用程序,同时支持多个平台;比官方要强; 官方的autoUpdater仅支持macOS 和 Windows 自动更新; 注意是自动,直接更新那种; 脚手架中是…...

React native之全局变量存储AsyncStorage
AsyncStorage是React native中对变量,对象进行全局存储,读取的异步使用对象。以key值进行存储。但是只能存储字符串数据,想存储对象,可把对象JSON进行序列化存储,读取的时候再转成JSON对象。 AsyncStorage.getItem()-…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...
