导数的概念及在模型算法中的应用

一. 导数概念与计算

1.  导数的物理意义：

瞬时速率。一般的，函数y=f(x)在x=处的瞬时变化率是

2.  导数的几何意义：

曲线的切线，当点趋近于P时，直线 PT 与曲线相切。容易知道，割线的斜率是当点趋近于 P 时，函数y=f(x)在x=处的导数就是切线PT的斜率k，即

3.  导函数：当x变化时，便是x的一个函数，我们称它为f（x）的导函数. y=f（x）的导函数有时也记作，即

2. 导数的计算

基本初等函数的导数公式：

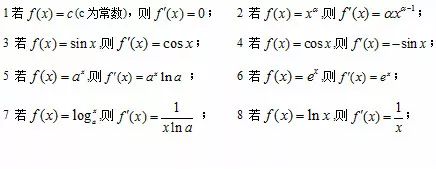
导数的运算法则：

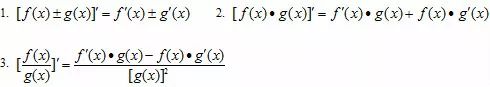
复合函数求导 ：

y=f(u)和u=g(x)，则称y可以表示成为x的函数，即y=f(g(x))为一个复合函数。

3、导数在研究函数中的应用

1.  函数的单调性与导数：  一般的，函数的单调性与其导数的正负有如下关系：

在某个区间（a,b）内

(1) 如果＞0，那么函数y=f(x)在这个区间单调递增；

(2) 如果＜0，那么函数y=f(x)在这个区间单调递减；

2.  函数的极值与导数：极值反映的是函数在某一点附近的大小情况。

 求函数y=f(x)的极值的方法有：

（1）如果在附近的左侧＞0 ，右侧＜0，那么是极大值；

（2）如果在附近的左侧＜0 ，右侧＞0，那么是极小值；

3.  函数的最大(小)值与导数：             

求函数y=f(x)在［a,b］上的最大值与最小值的步骤：

（1）求函数y=f(x)在［a,b］内的极值；

（2） 将函数y=f(x)的各极值与端点处的函数值f(a)，f(b)比较，其中最大的是最大值，最小的是最小值。

4.  推理与证明

（1）合情推理与类比推理根据一类事物的部分对象具有某种性质，推出这类事物的所有对象都具有这种性质的推理，叫做归纳推理,归纳是从特殊到一般的过程，它属于合情推理。根据两类不同事物之间具有某些类似（或一致）性，推测其中一类事物具有与另外一类事物类似的性质的推理，叫做类比推理。

类比推理的一般步骤：

(1)   找出两类事物的相似性或一致性；

(2)   用一类事物的性质去推测另一类事物的性质,得出一个明确的命题（猜想）；

(3)   一般的，事物之间的各个性质并不是孤立存在的,而是相互制约的.如果两个事物在某些性质上相同或相似，那么他们在另一写性质上也可能相同或类似,类比的结论可能是真的；

(4)   一般情况下，如果类比的相似性越多，相似的性质与推测的性质之间越相关，那么类比得出的命题越可靠。

演绎推理（俗称三段论）由一般性的命题推出特殊命题的过程,这种推理称为演绎推理。、（3）数学归纳法1.   它是一个递推的数学论证方法。2.   步骤：A. 命题在 n=1（或）时成立，这是递推的基础；B.假设在 n=k 时命题成立； C. 证明 n=k+1 时命题也成立。

完成这两步，就可以断定对任何自然数（或n≥，且n∈N）结论都成立。证明方法：1、 反证法；2、分析法；3、综合法。

导数在人工智能（AI）和机器学习（ML）领域起着关键性作用，主要体现在优化算法、模型训练、特征选择、深度学习中。比如，在模型训练过程中，导数帮助我们理解模型响应变化的敏感程度，对模型进行调整，以找到损失函数的最小值。这一过程是通过计算损失函数对模型参数的导数（即梯度）并使用这些导数信息来更新模型参数实现的。

二、导数优化算法

优化算法是机器学习和人工智能中最基本且至关重要的一环，其目标是最小化或最大化一个目标函数。导数在这一过程中发挥了核心作用。梯度下降（Gradient Descent）是一个通过导数指导参数更新以最小化损失函数的经典算法。在每一步更新中，我们计算损失函数对参数的偏导数（梯度），然后按照梯度的反方向调整参数，以期减少损失。这是基于导数的一个核心概念——导数给出了函数增长最快的方向。

首先，确定损失函数，它是评价模型好坏的尺度。接着，计算损失函数对每个参数的导数，即梯度。最后，利用这些梯度信息更新模型参数，逐渐逼近最佳模型参数配置。

二、导数模型训练

在模型训练过程中，导数的使用对于模型的学习效果具有决定性影响。通过计算损失函数相对于模型参数的导数，可以确定参数调整的方向和步幅，以有效地减少模型误差。这一过程称为反向传播（Backpropagation），是训练神经网络的关键步骤。

反向传播的基础是链式法则，它允许我们有效计算复杂函数的导数。通过链式法则，我们可以将复杂的函数分解为简单函数的组合，逐步计算每个部分的导数，从而高效计算整个函数的梯度。

三、导数特征选择

在机器学习中，特征选择是挑选出对模型预测最有贡献的特征的过程。导数在此处发挥作用，通过评估特征对模型输出的影响程度，即计算损失函数关于每个特征的导数，帮助选择出最有信息量的特征。这能显著提高模型的训练效率和预测性能。

特征选择不仅能减少模型的复杂度，还能避免过拟合，提高模型的泛化能力。通过剔除不重要的特征，保留最关键的特征，能够让模型更加专注于重要信息，提高训练和预测的效率。

四、深度学习中的导数

在深度学习领域，导数的作用尤为显著。深度学习模型通常包含大量的参数，通过反向传播算法，即通过计算损失函数对各层参数的偏导数来更新这些参数。这一过程要求对每一层的运算都精确计算其梯度，以确保参数在正确的方向上调整。

深度学习模型之所以能处理复杂的非线性问题，得益于其深层结构和非线性激活函数的组合，而导数在激活函数的选择和模型训练过程中起着至关重要的作用。通过精确的导数计算，不仅可以有效训练模型，还可以通过调整网络结构中的超参数来优化模型性能。

五、相关问答FAQs：

什么是导数在人工智能和机器学习中的作用？

导数在人工智能和机器学习中起到了关键的作用。通过计算导数，我们可以衡量目标函数在某个点的斜率，从而确定最优解的方向和速度。

导数如何在人工智能和机器学习中应用？

在人工智能和机器学习中，导数被用于优化算法。例如，在梯度下降算法中，我们利用导数来更新模型参数，以逐步接近最优解。

举例说明导数在人工智能和机器学习中的具体应用场景。

      导数在人工智能和机器学习中广泛应用于各种任务中。例如，在图像识别中，我们可以通过计算图像像素值的导数来检测边缘和纹理。在自然语言处理中，导数可以用来优化语言模型的参数，提高文本生成的质量。在强化学习中，导数可以帮助我们确定最优动作策略，从而让机器智能地与环境交互。总之，导数在人工智能和机器学习中扮演着重要的角色，能够帮助我们优化模型和算法，取得更好的效果。

导数作用结论

    通过对导数在人工智能和机器学习中多个方面的作用进行了详细阐述，我们可以看到导数不仅在理论上具有重要意义，而且在实际应用中发挥着至关重要的作用。它是优化算法的基石，是模型训练过程中不可或缺的工具，是特征选择的依据，也是深度学习实现复杂非线性拟合的关键。因此，深入理解和掌握导数的应用，对于在人工智能和机器学习领域取得成功至关重要。