第2讲 数据库系统的结构抽象与演变
基本内容
- 数据库系统的标准结构?
- 数据模型?
- 数据库系统的演变与发展?
重难点
- 一组概念的区分：三级模式两层映像，物理独立性和逻辑独立性
- 一组概念的区分：数据→模式→数据模型
- 几种数据模型的差异：网状/层次模型→关系模型→数据模型
数据库系统的标准结构
(1)数据库系统的分层抽象
- DBMS管理数据的三个层次
- External Level = User Level
- 某一用户能够看到与处理的数据, 全局数据中的某一部分
- Conceptual Level = Logic level
- 从全局角度理解/管理的数据, 含相应的关联约束
- Internal Level = Physical level
- 存储在介质上的数据，含存储路径、存储方式、索引方式等
(2)数据(视图)与模式
模式(Schema)
- 对数据库中数据所进行的一种结构性的描述
- 所观察到数据的结构信息
视图(View)/数据(Data)
- 某一种表现形式下表现出来的数据库中的数据
(3)三级模式两层映像
三级模式
- External Schema ---- (External) View
- 某一用户能够看到与处理的数据的结构描述
- (Conceptual) Schema ---- Conceptual View
- 从全局角度理解/管理的数据的结构描述, 含相应的关联约束
- 体现在数据之间的内在本质联系
- Internal Schema ---- Internal View
- 存储在介质上的数据的结构描述，含存储路径、存储方式、索引方式等
两层映像
- E-C Mapping：External Schema-Conceptual Schema Mapping
- 将外模式映射为概念模式，从而支持实现数据概念视图向外部视图的转换
- 便于用户观察和使用
- C-I Mapping：Conceptual Schema-Internal Schema Mapping
- 将概念模式映射为内模式，从而支持实现数据概念视图向内部视图的转换
- 便于计算机进行存储和处理
(4)数据库系统的标准结构 --> 三层模式两层映像
(5)两个
相关文章：
第2讲 数据库系统的结构抽象与演变
基本内容 数据库系统的标准结构?数据模型?数据库系统的演变与发展?重难点 一组概念的区分：三级模式两层映像，物理独立性和逻辑独立性一组概念的区分：数据→模式→数据模型几种数据模型的差异：网状/层次模型→关系模型→数据模型数据库系统的标准结构 (1)数据库系统的分…...
Git创建开发分支命名规则
git checkout -b feature/branchname 和 git checkout -b branchname 这两条命令的主要区别在于新分支的命名。 主要区别 分支命名： git checkout -b feature/branchname：新分支的名字是 feature/branchname，表示该分支属于一个特性开发&…...
【纯前端excel导出】vue2纯前端导出excel，使用xlsx插件，修改样式、合并单元格
一、使用第三方插件 1、安装 npm install xlsx-js-style 2、引入 import xlsx from xlsx-js-style xlsx插件是基础的导出，不可以修改样式，直接xlsx-style插件式修改样式的，所以这里直接用二者合体插件即可 二、页面使用 1、数据源 [{"…...
如何在极速浏览器中实现谷歌浏览器的扩展功能
在当今数字化时代，浏览器扩展功能极大地增强了我们的在线体验。尤其是谷歌浏览器，以其丰富的扩展生态而闻名。但是，如果你想在极速浏览器中使用这些谷歌浏览器的扩展功能，该怎么办呢？本文将为你详细解析如何实现这一目…...
Web安全 - 跨站点请求伪造CSRF（Cross Site Request Forgery）
文章目录 OWASP 2023 TOP 10CSRF 导图CSRF的基本概念CSRF的工作原理常见CSRF攻击模式CSRF防御策略补充建议应用场景实战防御策略选择1. CSRF Token（首选）2. SameSite Cookie属性3. 验证Referer和Origin4. 多因素认证 实现方案CSRF Token实现SameSite Coo…...
C++游戏开发完整学习路径
C游戏开发完整学习路径 引言 随着游戏行业的迅速发展，C作为主要的游戏开发语言，因其高效性和灵活性，依然受到广泛欢迎。C不仅在大型游戏开发中被广泛使用，而且在游戏引擎的构建、性能优化和复杂算法的实现中也扮演着关键角色。本…...
vue3之 shallowRef、markRaw
shallowRef 用于创建一个浅层响应式引用，只对顶层属性进行响应式处理。 markRaw 用于标记一个对象，使其完全跳过 Vue 的响应式系统。 这两者都可以用于优化性能，避免不必要的响应式开销，特别是在处理大型对象或第三方库对象时。 …...
影刀RPA实战：操作Mysql数据库
1.摘要 影刀RPA（Robotic Process Automation）是一种软件自动化工具，它可以模拟人类用户执行各种重复性任务，其中包括对数据库的操作。 我们可以使用软件自动化指令，通过获取数据库窗口对象来操作数据库，也…...
【c++】c++11多线程开发
2 C多线程 本文是参考爱编程的大丙c多线程部分内容，按照自己的理解对其进行整理的一篇学习笔记，具体一些APi的详细说明请参考大丙老师教程。 代码性能的问题主要包括两部分的内容，一个是前面提到资源的获取和释放，另外一个就是多…...
PW37R_V1 产品规格书
概述 PW37R_V1是一款采用3.7英寸黑白红三色电子纸显示的电子标签，采用一种先进的无线自动更新系统，实现无线传输。 通过http，mqtt协议更新数据和控制该款电子标签的显示等操作，显示内容可自定义。内置电池供电，可Typ…...
android11 usb摄像头添加多分辨率支持
部分借鉴于：https://blog.csdn.net/weixin_45639314/article/details/142210634 目录 一、需求介绍 二、UVC介绍 三、解析 四、补丁修改 1、预览的限制主要存在于hal层和framework层 2、添加所需要的分辨率： 3、hal层修改 4、frameworks 5、备…...
【开源免费】基于SpringBoot+Vue.JS房屋租赁系统（JAVA毕业设计）
本文项目编号 T 020 ，文末自助获取源码 \color{red}{T020，文末自助获取源码} T020，文末自助获取源码 目录 一、系统介绍二、演示录屏三、启动教程四、功能截图五、文案资料5.1 选题背景5.2 国内外研究现状5.3 可行性分析 六、核心代码6.1 查…...
JavaScript全面指南(二)
🌈个人主页：前端青山 🔥系列专栏：Javascript篇 🔖人终将被年少不可得之物困其一生 依旧青山,本期给大家带来JavaScript篇专栏内容:JavaScript全面指南(二) 目录 21、说明如何使用JavaScript提交表单？ 2…...
Nginx：Linux配置Nginx
目录 一、环境安装1.1 GCC编译器1.2 PCRE1.3 Zlib1.4 OpenSSL1.5 快速下载 二、Nginx源码简单安装2.1 下载安装包2.2 解压2.3 进入资源文件中2.4 编译、安装 三、Yum安装四、Nginx源码复杂安装4.1 参数介绍4.2 参数配置 五、卸载Nginx5.1 关闭Nginx进程5.2 将安装的Nginx删除5.…...
WebRTC音频 04 - 关键类
WebRTC音频01 - 设备管理 WebRTC音频 02 - Windows平台设备管理 WebRTC音频 03 - 实时通信框架 WebRTC音频 04 - 关键类(本文) 一、前言： 在WebRTC音频代码阅读过程中，我们发现有很多关键的类比较抽象，搞不清楚会导致代码阅读一脸懵逼。比如…...
Elasticsearch：Redact（编辑） processor
Redact 处理器使用 Grok 规则引擎来隐藏输入文档中与给定 Grok 模式匹配的文本。该处理器可用于隐藏个人身份信息 (Personal Identifying Information - PII)，方法是将其配置为检测已知模式，例如电子邮件或 IP 地址。与 Grok 模式匹配的文本将被替换为可…...
O2OA结合备份脚本和定时任务进行数据库的备份，我们以MySQL数据库为例
概述 系统运行一段时间后，可能发生各种情况导致数据丢失，如硬件故障、人为错误、软件错误、病毒攻击等。定期备份可以帮助您保护数据免受这些风险的影响，以便在需要时能够恢复数据。 O2OA应用本身可以通过dump配置每天自定备份数据ÿ…...
Python自动化办公：批量提取PDF中的表格到Excel
在现代办公环境中，处理大量的PDF文件并提取其中的表格数据是一项常见而繁琐的任务。手动复制粘贴不仅耗时耗力，还容易出错。Python作为一种功能强大的编程语言，提供了丰富的工具包，可以高效地解决这一问题。本文将介绍如何使用Pyt…...
selenium有多个frame页时的操作方法（5）
之前文章我们提到，在webdriver.WebDriver类有一个switch_to方法，通过switch_to.frame()可以切换到不同的frame页然后才再定位某个元素做一些输入/点击等操作。 比如下面这个测试网站有2个frame页：http://www.sahitest.com/demo/framesTest.h…...
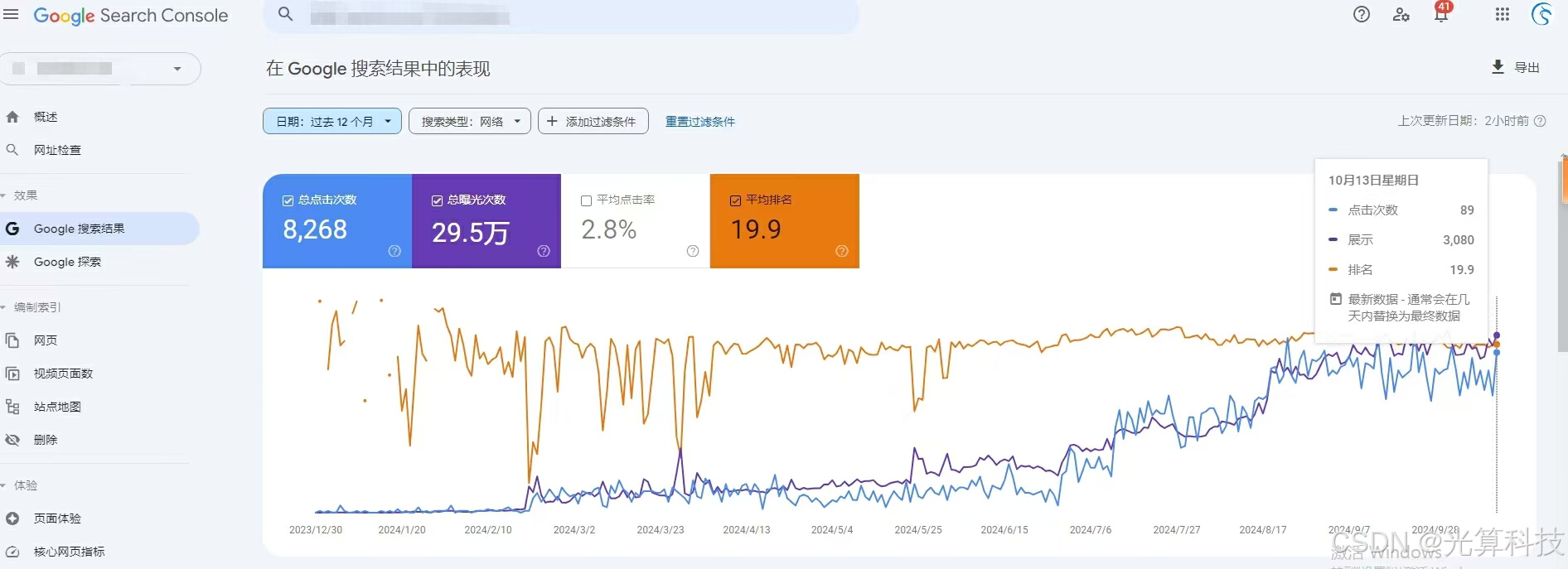
谷歌外链的周期性维护！
外链建设不是一次性的工作，它需要长期的维护和更新，才能持续为网站带来稳定的流量和SEO提升。很多网站在初期通过短期内大规模获取外链的方式，确实能看到排名的提升，但这种方法往往难以维持长期的效果。谷歌更喜欢自然、持续增长的…...
观成科技：隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具，该工具基于TUN接口实现其功能，利用反向TCP/TLS连接建立一条隐蔽的通信信道，支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式，适应复杂网…...
eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明： 想象一下，你正在用eNSP搭建一个虚拟的网络世界，里面有虚拟的路由器、交换机、电脑（PC）等等。这些设备都在你的电脑里面“运行”，它们之间可以互相通信，就像一个封闭的小王国。 但是&#…...
聊聊 Pulsar：Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台，以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中，Producer（生产者） 是连接客户端应用与消息队列的第一步。生产者…...
P3 QT项目----记事本（3.8）
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...
React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store： 我们在使用异步的时候理应是要使用中间件的，但是configureStore 已经自动集成了 redux-thunk，注意action里面要返回函数 import { configureS…...
JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念，确保一个租户（在这个系统中可能是一个公司或一个独立的客户）的数据对其他租户是不可见的。在 RuoYi 框架（您当前项目所使用的基础框架）中，这通常是通过在数据表中增加一个…...
中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学？传统医学奠基期（远古 - 17 世纪）近代医学转型期（17 世纪 - 19 世纪末）现代医学成熟期（20世纪至今） 中医的源远流长和一脉相承远古至…...
PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...
处理vxe-table 表尾数据是单独一个接口，表格tableData数据更新后，需要点击两下，表尾才是正确的
修改bug思路： 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑：async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...
三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值，最大值左侧的数值严格单调递增，最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值，最小值左侧的数值严格单调递减，最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...