【优选算法】——双指针(上篇)!

🌈个人主页:秋风起,再归来~
🔥系列专栏:C++刷题算法总结
🔖克心守己,律己则安
目录
前言:双指针
1. 移动零(easy)
2. 复写零(easy)
3. 快乐数(medium)
4. 盛⽔最多的容器(medium)
5. 完结散花
前言:双指针
常⻅的双指针有两种形式,⼀种是对撞指针,⼀种是左右指针。
对撞指针:⼀般⽤于顺序结构中,也称左右指针。
• 对撞指针从两端向中间移动。⼀个指针从最左端开始,另⼀个从最右端开始,然后逐渐往中间逼 近。
• 对撞指针的终⽌条件⼀般是两个指针相遇或者错开(也可能在循环内部找到结果直接跳出循 环),也就是:
◦ left == right (两个指针指向同⼀个位置)
◦ left > right (两个指针错开)
快慢指针:⼜称为⻳兔赛跑算法,其基本思想就是使⽤两个移动速度不同的指针在数组或链表等序列 结构上移动。
这种⽅法对于处理环形链表或数组⾮常有⽤。
其实不单单是环形链表或者是数组,如果我们要研究的问题出现循环往复的情况时,均可考虑使⽤快 慢指针的思想。 快慢指针的实现⽅式有很多种,
最常⽤的⼀种就是:
• 在⼀次循环中,每次让慢的指针向后移动⼀位,⽽快的指针往后移动两位,实现⼀快⼀慢。
1. 移动零(easy)
「数组分两块」是⾮常常⻅的⼀种题型,主要就是根据⼀种划分⽅式,将数组的内容分成左右两部 分。这种类型的题,⼀般就是使⽤「双指针」来解决。
题目链接![]() https://leetcode.cn/problems/move-zeroes/
https://leetcode.cn/problems/move-zeroes/
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
示例 1:
输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]
示例 2:输入: nums = [0]
输出: [0]
进阶:你能尽量减少完成的操作次数吗?
解题思路:
1、我们先定义两个指针cur和pre。
2、我们用cur来扫描整个数组。
a、如果cur位置为0,我们不进行处理,cur++。
b、如果cur位置不为0,我们让cur位置和pre位置的元素交换,pre++,cur++。
3、通过以上的操作,我们把该数组进行了区域划分:[0,pre)区域的元素是非零的,[pre,cur)区域的元素是0,而[cur,len)区域是没有判断的区域。
4、循环以上的操作,当cur走到数组末尾时,结束循环。
具象图
抽象图
 解题代码:
解题代码:
class Solution {
public:void moveZeroes(vector<int>& nums) {int len=nums.size();for(int cur=0,pre=0;cur<len;cur++){if(nums[cur]!=0) swap(nums[cur],nums[pre++]);}}
};2. 复写零(easy)
题目链接![]() https://leetcode.cn/problems/duplicate-zeros/description/
https://leetcode.cn/problems/duplicate-zeros/description/
给你一个长度固定的整数数组 arr ,请你将该数组中出现的每个零都复写一遍,并将其余的元素向右平移。
注意:请不要在超过该数组长度的位置写入元素。请对输入的数组 就地 进行上述修改,不要从函数返回任何东西。
示例 1:
输入:arr = [1,0,2,3,0,4,5,0]
输出:[1,0,0,2,3,0,0,4]
解释:调用函数后,输入的数组将被修改为:[1,0,0,2,3,0,0,4]
示例 2:输入:arr = [1,2,3]
输出:[1,2,3]
解释:调用函数后,输入的数组将被修改为:[1,2,3]
解题思路:
1、我们先定义两个指针cur=-1,des=1。
2、cur扫描数组:
a、cur位置为0,des走两步
b、cur位置不为0,des走一步
3、当des大于等于len-1位置时结束循环
4、cur的作用是走到最终被重写的元素,而des的作用是找到我们从后往前复写开始的位置
5、如果我们从前往后复写的话,有可能会把我们需要复写的元素覆盖!

int cur = -1;int des = -1;int len = arr.size();while (des < len-1){cur++;if (arr[cur] == 0)des += 2;elsedes++;}6、处理边界情况,如果最后一个要复写的元素是0,那么des的位置会走到len(即数组的长度不够我们复写两个0),这时我们要单独处理这种情况,提前复写一个0即可。

if (des == len){cur--;arr[des - 1] = 0;des -= 2;}7、从前往后复写
while (cur >= 0){if (arr[cur] == 0){arr[des--] = 0;arr[des--] = 0;}else arr[des--] = arr[cur];cur--;}解题代码:
class Solution
{
public:void duplicateZeros(vector<int>& arr){int cur = -1;int des = -1;int len = arr.size();//找到最后一个数while (des < len-1){cur++;if (arr[cur] == 0)des += 2;elsedes++;}//处理边界情况if (des == len){cur--;arr[des - 1] = 0;des -= 2;}//从后往前复写while (cur >= 0){if (arr[cur] == 0){arr[des--] = 0;arr[des--] = 0;}else arr[des--] = arr[cur];cur--;}}
};3. 快乐数(medium)
题目链接![]() https://leetcode.cn/problems/happy-number/description/
https://leetcode.cn/problems/happy-number/description/
编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」 定义为:
对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。
然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。
如果这个过程 结果为 1,那么这个数就是快乐数。
如果 n 是 快乐数 就返回 true ;不是,则返回 false 。示例 1:
输入:n = 19
输出:true
解释:
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1
示例 2:输入:n = 2
输出:false
解题思路:


1、通过分析以上两个例子,我们会发现当数字为快乐数时,它其实是在1当中死循环,当数字不是快乐数时,它其实是以自己初识位置为起点,但不能变化为一,最后进入一个死循环的过程。
2、而我们只要找到这个过程当中刚进入循环的数字是否为1即可判断该数字是否是快乐数。
3、我们可以快速的联想到链表当中的一个经典题型,这题也是如此,我们只要用快慢指针的思想就可以解决这个问题!
思考:为什么数字的变化一定只有这两种情况呢?
1、变为1后进入死循环。
2、最后没有变为1进入死循环。
还有一种情况:一直变化,不进入循环。(可能吗?)
题目说明了n的最大值是2^31-1即2,147,483,647。取最大值的每一位的平方和为260,所以n变化所得结果的范围在1~260之间。假设n从开始非常不幸经过了260次变化,恰好1~260之间的数字都变化得到过,那在261次变化时,其结果一定是1~260之间的某个元素,所以这个过程中一定会进入循环!(鸽巢原理)
4. 盛⽔最多的容器(medium)
题目链接![]() https://leetcode.cn/problems/container-with-most-water/description/
https://leetcode.cn/problems/container-with-most-water/description/
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明:你不能倾斜容器。
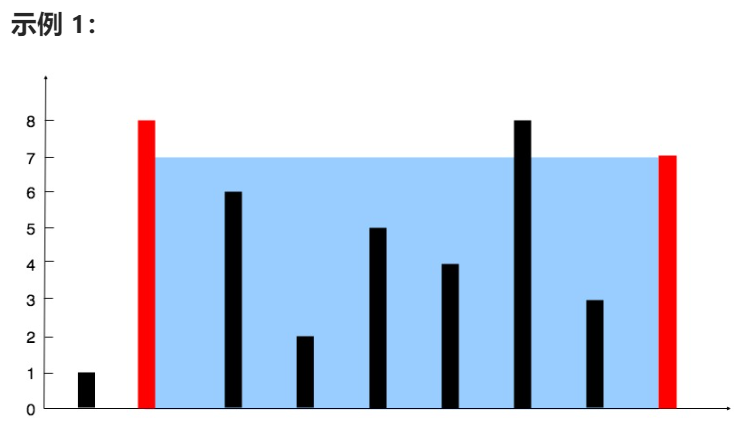
输入:[1,8,6,2,5,4,8,3,7]
输出:49
解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例 2:输入:height = [1,1]
输出:1
解题思路:
1、暴力枚举:这种题目我们最先想到的就是暴力枚举所有的面积,然后不断更新结果,找到最大的面积即可。不过这种n^2的算法一般在leetcode中等题型上提交都会超出时间的限制。
class Solution {
public:int maxArea(vector<int>& height) {int len=height.size();int ret=0;for(int left=0;left<len-1;left++){for(int right=1;right<len;right++){int tmp=(right-left)*min(height[left],height[right]);ret=max(tmp,ret);}}return ret;}
};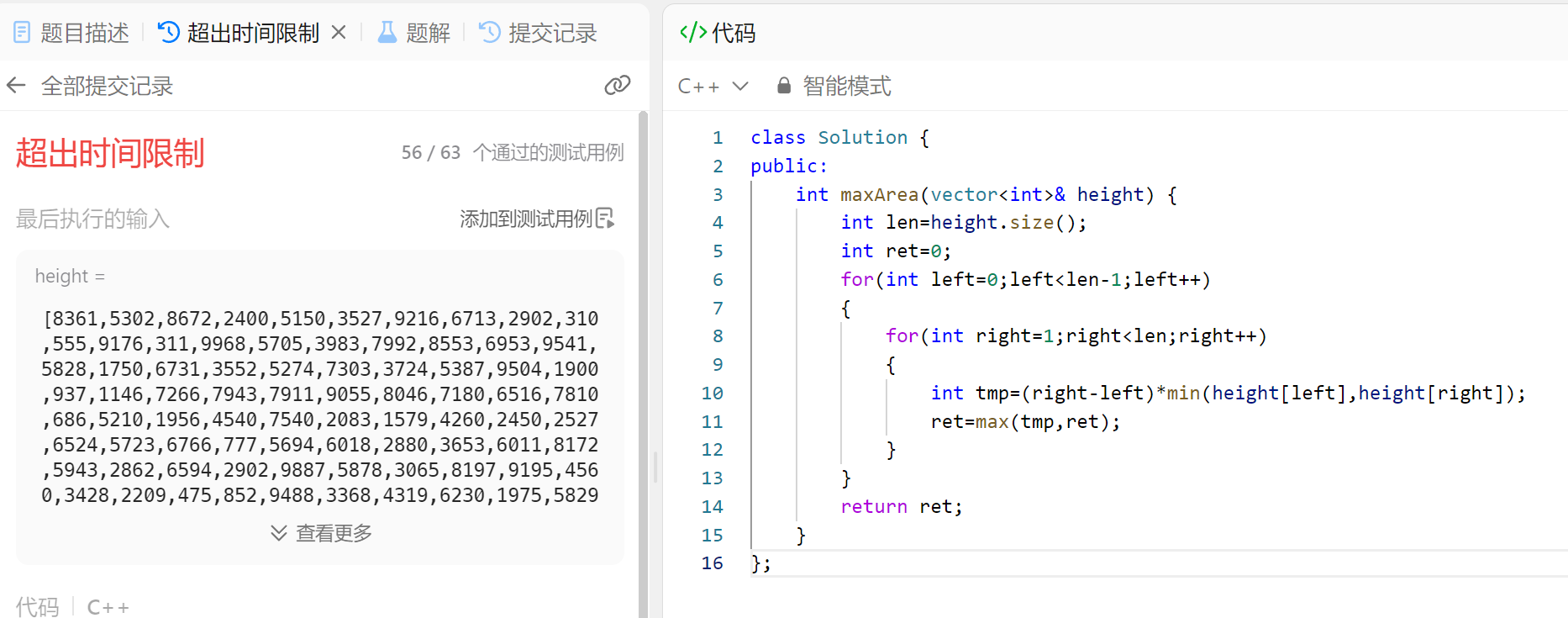
2、不过尽管如此,暴力解决问题的算法还是有其意义的,我们一般很难直接想到最优解法,所以我们可以在暴力解法的基础上去不断进行优化!
更优解法:
3、我可以定义left在数组的开头,right在数组的结尾。记录此时的面积,然后比较这两个位置的数值大小。
a.我们先固定数值较小(假设是left)的位置,然后移动数值较大(right)的一侧。这时我们会发现移动数值较大一侧元素时,枚举的所有情况的面积都是减小的!原因在于:首先宽是不断减小的,如果高right减小,总高度减小,如果增大,高度不变。这也就意味着固定left(较小一侧)位置所枚举的最大值就是当前位置,此时right就不再需要左移去,枚举其他情况(没有意义)!而此时固定较小端的所有情况就相当于枚举完了。
b.接着我们就让较小端的一侧++或--,循环知道left==right。此时所有情况都以枚举完成,我们只要将最大的结果记录下来就完了。

解题代码:
class Solution {
public:int maxArea(vector<int>& height) {int len=height.size();int left=0,right=len-1,ret=0;while(left<right){//更新结果int tmp=(right-left)*min(height[left],height[right]);ret=max(ret,tmp);//if(height[left]<height[right]) left++;else right--;}return ret;}
};5. 完结散花
好了,这期的分享到这里就结束了~
如果这篇博客对你有帮助的话,可以用你们的小手指点一个免费的赞并收藏起来哟~
如果期待博主下期内容的话,可以点点关注,避免找不到我了呢~
我们下期不见不散~~


相关文章:

【优选算法】——双指针(上篇)!
🌈个人主页:秋风起,再归来~🔥系列专栏:C刷题算法总结🔖克心守己,律己则安 目录 前言:双指针 1. 移动零(easy) 2. 复写零(easy) 3…...
【C语言】数据输出格式控制
数据的输出格式修饰 常用两种: 整型中,输出数据左对齐、右对齐、占m位、不足m位前补0。浮点型中,默认通过四舍五入保留小数点后6位,通过参数设置保留小数点后n位。 #include <stdio.h> #define PI 3.14159 /* 功能&#x…...

Qt-界面优化选择器的用法(70)
目录 描述 使用 类型选择器 ID 选择器 并集选择器 子控件选择器 伪控制器 描述 QSS 的选择器⽀持以下⼏种 选择器⽰例说明全局选择器*选择所有的 widget.类型选择器 (type selector)QPushButton选择所有的 QPushButton 和其⼦类的控件.类选择器 (class selector).QPus…...
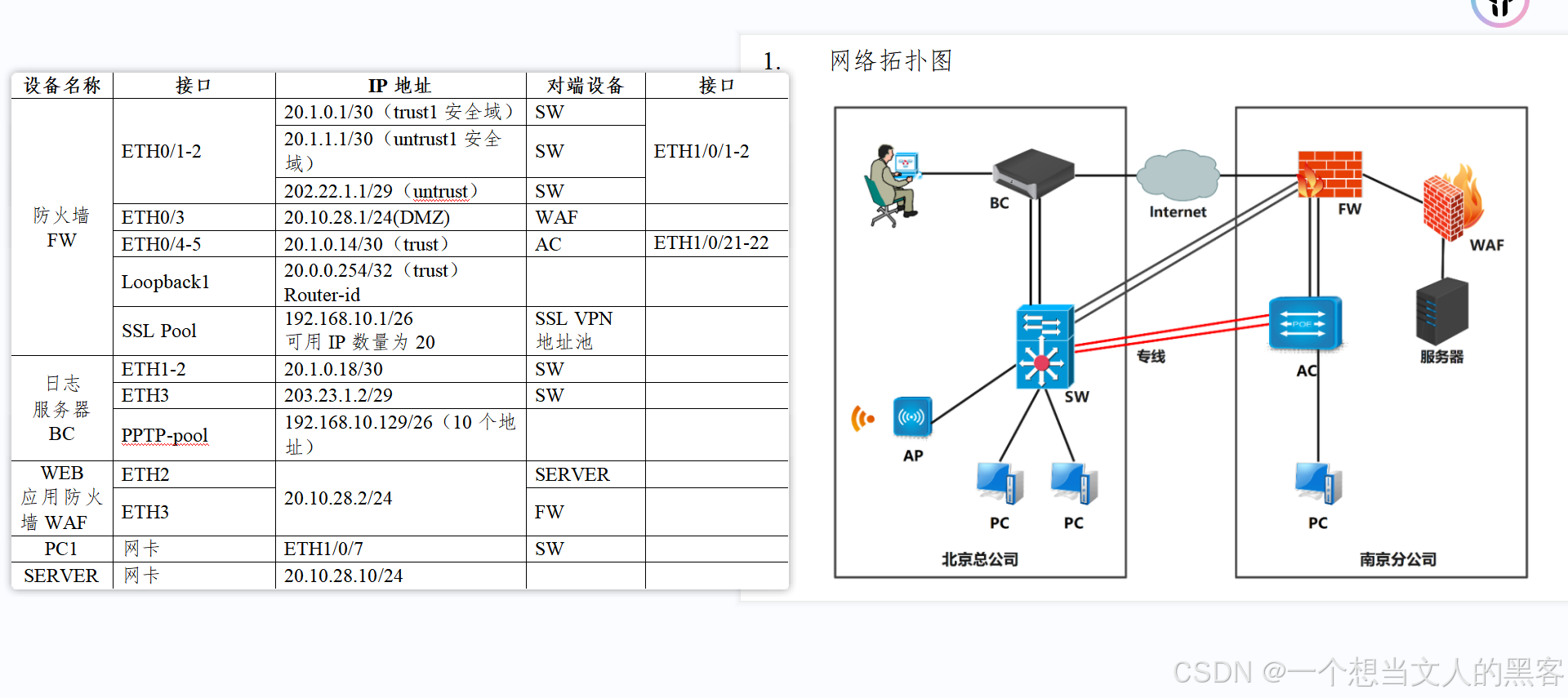
全国职业技能大赛——信息安全管理与评估第一阶段BC、FW、WAF题目详细解析过程
💗需要职业技能大赛环境+WP,请联系我!🍬 博主介绍 👨🎓 博主介绍:大家好,我是 一个想当文人的黑客 ,很高兴认识大家~ ✨主攻领域:【渗透领域】【应急响应】 【edusrc漏洞挖掘】 【VulnHub靶场复现】【面试分析】 🎉欢迎关注💗一起学习👍一起讨论⭐️一起…...
基于Vite创建项目
vite 是新一代前端构建工具,官网地址:https://vitejs.cn,vite的优势如下: 轻量快速的热重载(HMR),能实现极速的服务启动。对 TypeScript、JSX、CSS 等支持开箱即用。真正的按需编译,…...

面试题:在 React 中如何绑定事件
在 React 中绑定事件处理器(event handlers)是一个常见的任务,通常涉及以下几个步骤: 定义一个事件处理器函数:在组件的类或者函数组件内部定义一个处理事件的函数。 在 JSX 中绑定事件处理器:在渲染 JSX 时,使用 on 前缀加上事件名称(如 onClick, onChange, onSubmit …...

前端将JSON或者table直接导出为excel
一、引入Sheetjs或者npm直接下载 <script lang"javascript" src"https://cdn.sheetjs.com/xlsx-0.20.3/package/dist/xlsx.full.min.js"></script> 二、页面中使用 //json导出为excel <button onclick"exportExcel()">导出…...

算法之排序
概述 记录排序算法。 1 选择排序 *** 选择排序* 思路:遍历数组,找出(选择)最小的元素,然后和最左边的元素交换。接下来,再从第二个元素开始遍历整个数组。再找到最小的元素,再和第二个元素交换…...

深度学习:LSTM循环神经网络实现评论情感分析
目录 一、任务介绍 1.任务要求 2.信息内容 3.待思考问题 二、问题解决 1.将评论内容转换成语料库 2.获取每条评论的词向量、标签和长度 3.数据打包 4.建立LSTM循环神经网络模型 1.主程序代码 2.模型代码 5.建立训练集函数和测试集函数 一、任务介绍 1.任务要求 项…...

基于Arduino的环境监测装置
基于Arduino的环境监测装置 引言痛点功能前期准备软件硬件 项目开发硬件开发软件开发 功能演示更多精彩,欢迎关注 引言 本项目使用机智云Gokit2.0开发板,实现基于Arduino的环境监测装置,解决目前大多数人对环境数据要求逐渐增高的痛点。 痛…...
详解)
深度学习:模型攻击(Model Attack)详解
模型攻击(Model Attack)详解 模型攻击通常指在机器学习和人工智能领域中,故意设计的行为或方法,旨在操纵或欺骗机器学习模型的输出。这类攻击可能导致模型做出错误的决策或泄露敏感信息,对于安全性至关重要的应用&…...

CesiumLab介绍
软考鸭小程序 学软考,来软考鸭! 提供软考免费软考讲解视频、题库、软考试题、软考模考、软考查分、软考咨询等服务 CesiumLab是一个围绕Cesium平台设计的完整易用的数据预处理工具集,它旨在最大化提升三维数据可视化效率。本文将详细介绍CesiumLab的安装、主要功能…...

PyQt 入门教程(3)基础知识 | 3.2、加载资源文件
文章目录 一、加载资源文件1、PyQt5加载资源文件2、PyQt6加载资源文件 一、加载资源文件 常见的资源文件有图像与图标,下面分别介绍下加载资源文件的常用方法 1、PyQt5加载资源文件 2、PyQt6加载资源文件 PyQt6版本暂时没有提供pyrcc工具,下面介绍下在不…...

老照片修复工作流教程:用 ComfyUI 轻松还原历史记忆
你是否有过这样的遗憾? 那些珍贵的老照片因为时间的流逝,早已失去了当年的色彩,变得模糊、褪色,甚至破损? 今天带你了解如何使用 ComfyUI 的老照片修复工作流,通过简单的几步操作,在短短十几秒…...

ESP-IDF Blink实例学习
文章目录 一、引言二、工程创建1、打开vscode点击ESP-IDF资源管理器2、选择ESP-IDF框架3、选择Show Examples4、选择blink5、点击Create project using example blink ,选择创建目录6、创建完成 三、硬件电路LED管脚分配四、修改menuconfig五、编译和下载运行 一、引言 Blink实…...

QT QML 练习8-Simple Transformations
简单的转换(Simple Transformations) 转换操作改变了一个对象的几何状态。QML元素对象通常能够被平移,旋转,缩放。下面我们将讲解这些简单的操作和一些更高级的用法。 我们先从一个简单的转换开始。用下面的场景作为我们学习的开始…...

低空产业园搭建技术详解
低空产业园的搭建技术是一个复杂而系统的工程,涉及多个方面的技术和策略。以下是对低空产业园搭建技术的详细解析: 一、规划与设计 1. 总体规划:低空产业园的规划需要结合地方经济发展、产业基础、政策导向等因素,制定科学合理的…...

Python网络爬虫从入门到实战
目录 引言 一、网络爬虫的概念 二、 网络爬虫的基本工作流程 (一)过程: (二)安装requests模块和beautifulsoup4模块 (三)requests库的使用 1、requests库的基本介绍 2、导入requests库的…...

探索Theine:Python中的AI缓存新贵
文章目录 探索Theine:Python中的AI缓存新贵背景:为何选择Theine?Theine是什么?如何安装Theine?简单的库函数使用方法场景应用场景一:Web应用缓存场景二:分布式系统中的数据共享场景三࿱…...

js拼图(神鹰黑手哥)
直接上代码 再解释 这是最终效果图 css代码如下 * {margin: 0;padding: 0;}body {height: 800px;width: 100%;background-color: blanchedalmond;display: flex;justify-content: space-around;align-items: center;position: relative;}.img-box {display: flex;flex-wrap: w…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...