【高等数学】多元微分学(二)
隐函数的偏导数
二元方程的隐函数
F ( x , y ) = 0 F(x,y)=0 F(x,y)=0
推出隐函数形式 y = y ( x ) y=y(x) y=y(x). 欲求 d y d x \frac{d y}{d x} dxdy 需要对 F = 0 F=0 F=0 两边同时对 x x x 求全导
0 = d d x F ( x , y ( x ) ) = ∂ F ∂ x d x d x + ∂ F ∂ y d y d x = ∂ F ∂ x d x d x + ∂ F ∂ y d y d x 0 = \frac{d}{dx} F(x,y(x))= \frac{\partial F}{\partial x} \frac{dx}{dx}+\frac{\partial F}{\partial y} \frac{dy}{dx}=\frac{\partial F}{\partial x} \frac{dx}{dx}+\frac{\partial F}{\partial y} \frac{dy}{dx} 0=dxdF(x,y(x))=∂x∂Fdxdx+∂y∂Fdxdy=∂x∂Fdxdx+∂y∂Fdxdy
求出 d y d x = − ∂ F ∂ x ∂ F ∂ y \frac{dy}{dx}= -\frac{\frac{\partial F}{\partial x}}{\frac{\partial F}{\partial y}} dxdy=−∂y∂F∂x∂F
三元方程(组)的隐函数
三元方程
F ( x , y , z ) = 0 F(x,y,z)=0 F(x,y,z)=0,
推出隐函数形式 z = z ( x , y ) z=z(x,y) z=z(x,y). 欲求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z 需要对 F = 0 F=0 F=0 两边同时对 x x x 求偏导
0 = ∂ F ∂ x + ∂ F ∂ z ∂ z ∂ x 0=\frac{\partial F}{\partial x} +\frac{\partial F}{\partial z} \frac{\partial z}{\partial x} 0=∂x∂F+∂z∂F∂x∂z
求出 ∂ z ∂ x = − ∂ F ∂ x ∂ F ∂ z \frac{\partial z}{\partial x}= -\frac{\frac{\partial F}{\partial x}}{\frac{\partial F}{\partial z}} ∂x∂z=−∂z∂F∂x∂F
两个三元方程
F ( x , y , z ) = 0 F(x,y,z)=0 F(x,y,z)=0, G ( x , y , z ) = 0 G(x,y,z)=0 G(x,y,z)=0
推出隐函数形式 z = z ( x ) , y = y ( x ) z=z(x), y=y(x) z=z(x),y=y(x) 欲求 d z d x \frac{d z}{dx} dxdz 需要对 F = 0 , G = 0 F=0,G=0 F=0,G=0 两边同时对 x x x 求全导
0 = ∂ F ∂ x + ∂ F ∂ y d y d x + ∂ F ∂ z d z d x 0=\frac{\partial F}{\partial x}+\frac{\partial F}{\partial y}\frac{dy}{dx}+\frac{\partial F}{\partial z}\frac{dz}{dx} 0=∂x∂F+∂y∂Fdxdy+∂z∂Fdxdz
0 = ∂ G ∂ x + ∂ G ∂ y d y d x + ∂ G ∂ z d z d x 0=\frac{\partial G}{\partial x}+\frac{\partial G}{\partial y}\frac{dy}{dx}+\frac{\partial G}{\partial z}\frac{dz}{dx} 0=∂x∂G+∂y∂Gdxdy+∂z∂Gdxdz
根据克拉姆法则,
J = ∂ ( F , G ) ∂ ( y , z ) = ∣ ∂ F ∂ y ∂ F ∂ z ∂ G ∂ y ∂ G ∂ z ∣ J=\frac{\partial (F,G)}{\partial(y,z)}= \left|\begin{array}{c c} \frac{\partial F}{\partial y} &\frac{\partial F}{\partial z} \\\\ \frac{\partial G}{\partial y} &\frac{\partial G}{\partial z}\end{array}\right| J=∂(y,z)∂(F,G)= ∂y∂F∂y∂G∂z∂F∂z∂G
d y d x = − 1 J ∂ ( F , G ) ∂ ( x , z ) \frac{d y}{d x} = -\frac{1}{J} \frac{\partial (F, G)}{\partial (x,z)} dxdy=−J1∂(x,z)∂(F,G) d z d x = − 1 J ∂ ( F , G ) ∂ ( y , x ) \frac{d z}{d x} = -\frac{1}{J} \frac{\partial (F, G)}{\partial (y,x)} dxdz=−J1∂(y,x)∂(F,G)
四元方程(组)的隐函数
四元函数方程
F ( x , y , z , w ) = 0 F(x,y,z,w)=0 F(x,y,z,w)=0,
推出隐函数形式 w = w ( x , y , z ) w=w(x,y,z) w=w(x,y,z)
0 = ∂ F ∂ x + ∂ F ∂ w ∂ w ∂ x 0= \frac{\partial F}{\partial x}+\frac{\partial F}{\partial w} \frac{\partial w}{\partial x} 0=∂x∂F+∂w∂F∂x∂w 求出
∂ w ∂ x = − ∂ F ∂ x ∂ F ∂ w \frac{\partial w}{\partial x}= - \frac{\frac{\partial F}{\partial x}}{\frac{\partial F}{\partial w}} ∂x∂w=−∂w∂F∂x∂F 类似的
∂ w ∂ y = − ∂ F ∂ y ∂ F ∂ w \frac{\partial w}{\partial y}= - \frac{\frac{\partial F}{\partial y}}{\frac{\partial F}{\partial w}} ∂y∂w=−∂w∂F∂y∂F ∂ w ∂ z = − ∂ F ∂ z ∂ F ∂ w \frac{\partial w}{\partial z}= - \frac{\frac{\partial F}{\partial z}}{\frac{\partial F}{\partial w}} ∂z∂w=−∂w∂F∂z∂F
两个四元函数方程组
F ( x , y , z , w ) = 0 F(x,y,z,w)=0 F(x,y,z,w)=0, G ( x , y , z , w ) = 0 G(x,y,z,w)=0 G(x,y,z,w)=0 推出隐函数形式 z = z ( x , y ) z=z(x,y) z=z(x,y), w = w ( x , y ) w=w(x,y) w=w(x,y)
0 = ∂ F ∂ x + ∂ F ∂ z ∂ z ∂ x + ∂ F ∂ w ∂ w ∂ x 0=\frac{\partial F}{\partial x}+\frac{\partial F}{\partial z} \frac{\partial z}{\partial x}+\frac{\partial F}{\partial w} \frac{\partial w}{\partial x} 0=∂x∂F+∂z∂F∂x∂z+∂w∂F∂x∂w
0 = ∂ G ∂ x + ∂ G ∂ z ∂ z ∂ x + ∂ G ∂ w ∂ w ∂ x 0=\frac{\partial G}{\partial x}+\frac{\partial G}{\partial z} \frac{\partial z}{\partial x}+\frac{\partial G}{\partial w} \frac{\partial w}{\partial x} 0=∂x∂G+∂z∂G∂x∂z+∂w∂G∂x∂w
根据克拉姆法则, J = ∂ ( F , G ) ∂ ( z , w ) = ∣ ∂ F ∂ z ∂ F ∂ w ∂ G ∂ z ∂ G ∂ w ∣ J=\frac{\partial (F,G)}{\partial(z,w)}= \left|\begin{matrix}\frac{\partial F}{\partial z} &\frac{\partial F}{\partial w}\\\\\frac{\partial G}{\partial z} &\frac{\partial G}{\partial w}\end{matrix}\right| J=∂(z,w)∂(F,G)= ∂z∂F∂z∂G∂w∂F∂w∂G
∂ z ∂ x = − 1 J ∂ ( F , G ) ∂ ( x , w ) \frac{\partial z}{\partial x} = -\frac{1}{J} \frac{\partial (F, G)}{\partial (x,w)} ∂x∂z=−J1∂(x,w)∂(F,G) ∂ w ∂ x = − 1 J ∂ ( F , G ) ∂ ( z , x ) \frac{\partial w}{\partial x} = -\frac{1}{J} \frac{\partial (F, G)}{\partial (z,x)} ∂x∂w=−J1∂(z,x)∂(F,G)
类似的由 0 = ∂ F ∂ y + ∂ F ∂ z ∂ z ∂ y + ∂ F ∂ w ∂ w ∂ y 0=\frac{\partial F}{\partial y}+\frac{\partial F}{\partial z} \frac{\partial z}{\partial y}+\frac{\partial F}{\partial w} \frac{\partial w}{\partial y} 0=∂y∂F+∂z∂F∂y∂z+∂w∂F∂y∂w 0 = ∂ G ∂ y + ∂ G ∂ z ∂ z ∂ y + ∂ G ∂ w ∂ w ∂ y 0=\frac{\partial G}{\partial y}+\frac{\partial G}{\partial z} \frac{\partial z}{\partial y}+\frac{\partial G}{\partial w} \frac{\partial w}{\partial y} 0=∂y∂G+∂z∂G∂y∂z+∂w∂G∂y∂w 得到
∂ z ∂ y = − 1 J ∂ ( F , G ) ∂ ( y , w ) \frac{\partial z}{\partial y} = -\frac{1}{J} \frac{\partial (F, G)}{\partial (y,w)} ∂y∂z=−J1∂(y,w)∂(F,G) ∂ w ∂ y = − 1 J ∂ ( F , G ) ∂ ( z , y ) \frac{\partial w}{\partial y} = -\frac{1}{J} \frac{\partial (F, G)}{\partial (z,y)} ∂y∂w=−J1∂(z,y)∂(F,G)
三个四元函数方程组
F ( x , y , z , w ) = 0 F(x,y,z,w)=0 F(x,y,z,w)=0, G ( x , y , z , w ) = 0 G(x,y,z,w)=0 G(x,y,z,w)=0, H ( x , y , z , w ) = 0 H(x,y,z,w)=0 H(x,y,z,w)=0.
推出隐函数形式 y = y ( x ) , z = z ( x ) , w = w ( x ) y=y(x), z=z(x), w=w(x) y=y(x),z=z(x),w=w(x)
0 = ∂ F ∂ x + ∂ F ∂ y d y d x + ∂ F ∂ z d z d x + ∂ F ∂ w d w d x 0=\frac{\partial F}{\partial x}+\frac{\partial F}{\partial y} \frac{d y}{d x}+\frac{\partial F}{\partial z} \frac{d z}{d x}+\frac{\partial F}{\partial w} \frac{d w}{d x} 0=∂x∂F+∂y∂Fdxdy+∂z∂Fdxdz+∂w∂Fdxdw
0 = ∂ G ∂ x + ∂ G ∂ y d y d x + ∂ G ∂ z d z d x + ∂ G ∂ w d w d x 0=\frac{\partial G}{\partial x}+\frac{\partial G}{\partial y} \frac{d y}{d x}+\frac{\partial G}{\partial z} \frac{d z}{d x}+\frac{\partial G}{\partial w} \frac{d w}{d x} 0=∂x∂G+∂y∂Gdxdy+∂z∂Gdxdz+∂w∂Gdxdw
0 = ∂ H ∂ x + ∂ H ∂ y d y d x + ∂ H ∂ z d z d x + ∂ H ∂ w d w d x 0=\frac{\partial H}{\partial x}+\frac{\partial H}{\partial y} \frac{d y}{d x}+\frac{\partial H}{\partial z} \frac{d z}{d x}+\frac{\partial H}{\partial w} \frac{d w}{d x} 0=∂x∂H+∂y∂Hdxdy+∂z∂Hdxdz+∂w∂Hdxdw
由克拉姆法则,
J = ∂ ( F , G , H ) ∂ ( y , z , w ) = ∣ ∂ F ∂ y ∂ F ∂ z ∂ F ∂ w ∂ G ∂ y ∂ G ∂ z ∂ G ∂ w ∂ H ∂ y ∂ H ∂ z ∂ H ∂ w ∣ J= \frac{\partial(F, G, H)}{\partial (y,z,w)} = \left| \begin{array}{c c c} \frac{\partial F}{\partial y} &\frac{\partial F}{\partial z} & \frac{\partial F}{\partial w} \\\\ \frac{\partial G}{\partial y}&\frac{\partial G}{\partial z} &\frac{\partial G}{\partial w} \\\\ \frac{\partial H}{\partial y}&\frac{\partial H}{\partial z} &\frac{\partial H}{\partial w}\end{array}\right| J=∂(y,z,w)∂(F,G,H)= ∂y∂F∂y∂G∂y∂H∂z∂F∂z∂G∂z∂H∂w∂F∂w∂G∂w∂H
d y d x = − 1 J ∂ ( F , G , H ) ∂ ( x , z , w ) \frac{d y}{d x}=-\frac{1}{J} \frac{\partial (F,G,H)}{\partial (x,z,w)} dxdy=−J1∂(x,z,w)∂(F,G,H) d z d x = − 1 J ∂ ( F , G , H ) ∂ ( y , x , w ) \frac{d z}{d x}=-\frac{1}{J} \frac{\partial (F,G,H)}{\partial (y,x,w)} dxdz=−J1∂(y,x,w)∂(F,G,H) d w d x = − 1 J ∂ ( F , G , H ) ∂ ( y , z , x ) \frac{d w}{d x}=-\frac{1}{J} \frac{\partial (F,G,H)}{\partial (y,z,x)} dxdw=−J1∂(y,z,x)∂(F,G,H)
五元方程
两个五元方程
F ( x , y , z , u , v ) = 0 F(x,y,z,u,v)=0 F(x,y,z,u,v)=0, G ( x , y , z , u , v ) = 0 G(x,y,z,u,v)=0 G(x,y,z,u,v)=0
推出隐函数形式 u = u ( x , y , z ) , v = v ( x , y , z ) u=u(x,y,z), v=v(x,y,z) u=u(x,y,z),v=v(x,y,z), 对 F = 0 , G = 0 F=0, G=0 F=0,G=0 同时对 x x x 求偏微分
0 = ∂ F ∂ x + ∂ F ∂ u ∂ u ∂ x + ∂ F ∂ v ∂ v ∂ x 0= \frac{\partial F}{\partial x} + \frac{\partial F}{\partial u}\frac{\partial u}{\partial x} + \frac{\partial F}{\partial v}\frac{\partial v}{\partial x} 0=∂x∂F+∂u∂F∂x∂u+∂v∂F∂x∂v 0 = ∂ G ∂ x + ∂ G ∂ u ∂ u ∂ x + ∂ G ∂ v ∂ v ∂ x 0= \frac{\partial G}{\partial x} + \frac{\partial G}{\partial u}\frac{\partial u}{\partial x} + \frac{\partial G}{\partial v}\frac{\partial v}{\partial x} 0=∂x∂G+∂u∂G∂x∂u+∂v∂G∂x∂v
由克拉姆法则 J = ∂ ( F , G ) ∂ ( u , v ) J=\frac{\partial(F,G)}{\partial (u,v)} J=∂(u,v)∂(F,G), ∂ u ∂ x = − 1 J ∂ ( F , G ) ∂ ( x , v ) \frac{\partial u}{\partial x}=-\frac{1}{J}\frac{\partial(F,G)}{\partial(x,v)} ∂x∂u=−J1∂(x,v)∂(F,G) ∂ v ∂ x = − 1 J ∂ ( F , G ) ∂ ( u , x ) \frac{\partial v}{\partial x}=-\frac{1}{J}\frac{\partial(F,G)}{\partial(u,x)} ∂x∂v=−J1∂(u,x)∂(F,G)
类似的
∂ u ∂ y = − 1 J ∂ ( F , G ) ∂ ( y , v ) \frac{\partial u}{\partial y}=-\frac{1}{J}\frac{\partial(F,G)}{\partial(y,v)} ∂y∂u=−J1∂(y,v)∂(F,G) ∂ u ∂ y = − 1 J ∂ ( F , G ) ∂ ( u , y ) \frac{\partial u}{\partial y}=-\frac{1}{J}\frac{\partial(F,G)}{\partial(u,y)} ∂y∂u=−J1∂(u,y)∂(F,G)
∂ u ∂ z = − 1 J ∂ ( F , G ) ∂ ( z , v ) \frac{\partial u}{\partial z}=-\frac{1}{J}\frac{\partial(F,G)}{\partial(z,v)} ∂z∂u=−J1∂(z,v)∂(F,G) ∂ u ∂ z = − 1 J ∂ ( F , G ) ∂ ( u , z ) \frac{\partial u}{\partial z}=-\frac{1}{J}\frac{\partial(F,G)}{\partial(u,z)} ∂z∂u=−J1∂(u,z)∂(F,G)
三个五元方程
F ( x , y , z , u , v ) = 0 F(x,y,z,u,v)=0 F(x,y,z,u,v)=0, G ( x , y , z , u , v ) = 0 G(x,y,z,u,v)=0 G(x,y,z,u,v)=0, H ( x , y , z , u , v ) = 0 H(x,y,z,u,v)=0 H(x,y,z,u,v)=0
推出隐函数形式 z = z ( x , y ) , u = u ( x , y ) , v = v ( x , y ) z=z(x,y), u=u(x,y), v=v(x,y) z=z(x,y),u=u(x,y),v=v(x,y)
0 = ∂ F ∂ x + ∂ F ∂ z ∂ z ∂ x + ∂ F ∂ u ∂ u ∂ x + ∂ F ∂ v ∂ v ∂ x 0= \frac{\partial F}{\partial x} +\frac{\partial F}{\partial z}\frac{\partial z}{\partial x}+ \frac{\partial F}{\partial u}\frac{\partial u}{\partial x} + \frac{\partial F}{\partial v}\frac{\partial v}{\partial x} 0=∂x∂F+∂z∂F∂x∂z+∂u∂F∂x∂u+∂v∂F∂x∂v
0 = ∂ G ∂ x + ∂ G ∂ z ∂ z ∂ x + ∂ G ∂ u ∂ u ∂ x + ∂ G ∂ v ∂ v ∂ x 0= \frac{\partial G}{\partial x} +\frac{\partial G}{\partial z}\frac{\partial z}{\partial x}+ \frac{\partial G}{\partial u}\frac{\partial u}{\partial x} + \frac{\partial G}{\partial v}\frac{\partial v}{\partial x} 0=∂x∂G+∂z∂G∂x∂z+∂u∂G∂x∂u+∂v∂G∂x∂v
0 = ∂ H ∂ x + ∂ H ∂ z ∂ z ∂ x + ∂ H ∂ u ∂ u ∂ x + ∂ H ∂ v ∂ v ∂ x 0= \frac{\partial H}{\partial x} +\frac{\partial H}{\partial z}\frac{\partial z}{\partial x}+ \frac{\partial H}{\partial u}\frac{\partial u}{\partial x} + \frac{\partial H}{\partial v}\frac{\partial v}{\partial x} 0=∂x∂H+∂z∂H∂x∂z+∂u∂H∂x∂u+∂v∂H∂x∂v
由克拉姆法则 J = ∂ ( F , G , H ) ∂ ( z , u , v ) J=\frac{\partial(F,G,H)}{\partial (z,u,v)} J=∂(z,u,v)∂(F,G,H),
∂ z ∂ x = − 1 J ∂ ( F , G , H ) ∂ ( x , u , v ) \frac{\partial z}{\partial x}=-\frac{1}{J}\frac{\partial(F,G,H)}{\partial(x,u,v)} ∂x∂z=−J1∂(x,u,v)∂(F,G,H) ∂ u ∂ x = − 1 J ∂ ( F , G , H ) ∂ ( z , x , v ) \frac{\partial u}{\partial x}=-\frac{1}{J}\frac{\partial(F,G,H)}{\partial(z,x,v)} ∂x∂u=−J1∂(z,x,v)∂(F,G,H) ∂ v ∂ x = − 1 J ∂ ( F , G , H ) ∂ ( z , u , x ) \frac{\partial v}{\partial x}=-\frac{1}{J}\frac{\partial(F,G,H)}{\partial(z,u,x)} ∂x∂v=−J1∂(z,u,x)∂(F,G,H)
类似的 ∂ z ∂ y = − 1 J ∂ ( F , G , H ) ∂ ( y , u , v ) \frac{\partial z}{\partial y}=-\frac{1}{J}\frac{\partial(F,G,H)}{\partial(y,u,v)} ∂y∂z=−J1∂(y,u,v)∂(F,G,H) ∂ u ∂ y = − 1 J ∂ ( F , G , H ) ∂ ( z , y , v ) \frac{\partial u}{\partial y}=-\frac{1}{J}\frac{\partial(F,G,H)}{\partial(z,y,v)} ∂y∂u=−J1∂(z,y,v)∂(F,G,H) ∂ v ∂ y = − 1 J ∂ ( F , G , H ) ∂ ( z , u , y ) \frac{\partial v}{\partial y}=-\frac{1}{J}\frac{\partial(F,G,H)}{\partial(z,u,y)} ∂y∂v=−J1∂(z,u,y)∂(F,G,H)
(选看) 反函数的偏导数
一元一维函数 y = f ( x ) y=f(x) y=f(x)
反函数为 x = f − 1 ( y ) = ϕ ( y ) x=f^{-1}(y)=\phi(y) x=f−1(y)=ϕ(y)
ϕ ′ ( y ) = d x d y = 1 d y d x = 1 f ′ ( x ) = 1 f ′ ( ϕ ( y ) ) \phi'(y)=\frac{dx }{dy}=\frac{1}{\frac{dy}{dx}}=\frac{1}{f'(x)}=\frac{1}{f'(\phi(y))} ϕ′(y)=dydx=dxdy1=f′(x)1=f′(ϕ(y))1
二元二维函数 u ( x , y ) , v ( x , y ) u(x,y), v(x,y) u(x,y),v(x,y)
若在 x 0 , y 0 x_0,y_0 x0,y0 处满足 雅可比行列式 ∂ ( u , v ) ∂ ( x , y ) ≠ 0 \frac{\partial (u,v)}{\partial (x,y)}\neq 0 ∂(x,y)∂(u,v)=0, 则存在反函数 x = x ( u , v ) , y = y ( u , v ) x=x(u,v), y=y(u,v) x=x(u,v),y=y(u,v),
反函数的雅可比矩阵是原函数雅可比矩阵的逆
令
F ( x , y , u , v ) = x − x ( u ( x , y ) , v ( x , y ) ) = 0 F(x,y,u,v)=x-x(u(x,y),v(x,y))=0 F(x,y,u,v)=x−x(u(x,y),v(x,y))=0
G ( x , y , u , v ) = y − y ( u ( x , y ) , v ( x , y ) ) = 0 G(x,y,u,v)=y-y(u(x,y),v(x,y))=0 G(x,y,u,v)=y−y(u(x,y),v(x,y))=0
对 F = 0 F=0 F=0 G = 0 G=0 G=0 同时对 x x x 求偏导
1 = ∂ x ∂ u ∂ u ∂ x + ∂ x ∂ v ∂ v ∂ x 1= \frac{\partial x}{\partial u}\frac{\partial u}{\partial x}+\frac{\partial x}{\partial v}\frac{\partial v}{\partial x} 1=∂u∂x∂x∂u+∂v∂x∂x∂v
0 = ∂ y ∂ u ∂ u ∂ x + ∂ y ∂ v ∂ v ∂ x 0= \frac{\partial y}{\partial u}\frac{\partial u}{\partial x}+\frac{\partial y}{\partial v}\frac{\partial v}{\partial x} 0=∂u∂y∂x∂u+∂v∂y∂x∂v
对 F = 0 F=0 F=0 G = 0 G=0 G=0 同时对 y y y 求偏导
0 = ∂ x ∂ u ∂ u ∂ y + ∂ x ∂ v ∂ v ∂ y 0= \frac{\partial x}{\partial u}\frac{\partial u}{\partial y}+\frac{\partial x}{\partial v}\frac{\partial v}{\partial y} 0=∂u∂x∂y∂u+∂v∂x∂y∂v
1 = ∂ y ∂ u ∂ u ∂ y + ∂ y ∂ v ∂ v ∂ y 1= \frac{\partial y}{\partial u}\frac{\partial u}{\partial y}+\frac{\partial y}{\partial v}\frac{\partial v}{\partial y} 1=∂u∂y∂y∂u+∂v∂y∂y∂v
J = ∂ ( x , y ) ∂ ( u , v ) J=\frac{\partial (x,y)}{\partial (u,v)} J=∂(u,v)∂(x,y)
因此
∂ u ∂ x = 1 J ∂ y ∂ v \frac{\partial u}{\partial x}=\frac{1}{J}\frac{\partial y}{\partial v} ∂x∂u=J1∂v∂y
∂ v ∂ x = − 1 J ∂ y ∂ u \frac{\partial v}{\partial x}=-\frac{1}{J}\frac{\partial y}{\partial u} ∂x∂v=−J1∂u∂y
∂ u ∂ y = − 1 J ∂ x ∂ v \frac{\partial u}{\partial y}=-\frac{1}{J}\frac{\partial x}{\partial v} ∂y∂u=−J1∂v∂x
∂ v ∂ y = 1 J ∂ x ∂ u \frac{\partial v}{\partial y}=\frac{1}{J}\frac{\partial x}{\partial u} ∂y∂v=J1∂u∂x
用线性代数矩阵的乘法表示
[ ∂ x ∂ u ∂ x ∂ v ∂ y ∂ u ∂ y ∂ v ] [ ∂ u ∂ x ∂ u ∂ y ∂ v ∂ x ∂ v ∂ y ] = [ 1 0 0 1 ] \left[\begin{matrix}\frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{matrix}\right]\left[\begin{matrix} \frac{\partial u}{\partial x} & \frac{\partial u}{\partial y} \\ \frac{\partial v}{\partial x} & \frac{\partial v}{\partial y} \end{matrix}\right] =\left[\begin{matrix} 1 & 0\\ 0& 1 \end{matrix}\right] [∂u∂x∂u∂y∂v∂x∂v∂y][∂x∂u∂x∂v∂y∂u∂y∂v]=[1001]
三元三维函数 u = ( x , y , z ) , v ( x , y , z ) , w ( x , y , z ) u=(x,y,z), v(x,y,z), w(x,y,z) u=(x,y,z),v(x,y,z),w(x,y,z)
类似地
[ ∂ x ∂ u ∂ x ∂ v ∂ x ∂ w ∂ y ∂ u ∂ y ∂ v ∂ y ∂ w ∂ z ∂ u ∂ z ∂ v ∂ z ∂ w ] [ ∂ u ∂ x ∂ u ∂ y ∂ u ∂ z ∂ v ∂ x ∂ v ∂ y ∂ v ∂ z ∂ w ∂ x ∂ w ∂ y ∂ w ∂ z ] = [ 1 0 0 0 1 0 0 0 1 ] \left[\begin{matrix}\frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} & \frac{\partial x}{\partial w}\\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} & \frac{\partial y}{\partial w}\\ \frac{\partial z}{\partial u} & \frac{\partial z}{\partial v} & \frac{\partial z}{\partial w}\\ \end{matrix}\right]\left[\begin{matrix} \frac{\partial u}{\partial x} & \frac{\partial u}{\partial y} &\frac{\partial u}{\partial z}\\ \frac{\partial v}{\partial x} & \frac{\partial v}{\partial y} &\frac{\partial v}{\partial z}\\ \frac{\partial w}{\partial x} & \frac{\partial w}{\partial y} &\frac{\partial w}{\partial z}\\ \end{matrix}\right] =\left[\begin{matrix} 1 & 0& 0\\ 0& 1 &0\\ 0& 0 &1 \end{matrix}\right] ∂u∂x∂u∂y∂u∂z∂v∂x∂v∂y∂v∂z∂w∂x∂w∂y∂w∂z ∂x∂u∂x∂v∂x∂w∂y∂u∂y∂v∂y∂w∂z∂u∂z∂v∂z∂w = 100010001
(选看) 参数方程的微分
二维单参数方程 (一元二维)
x = x ( t ) x=x(t) x=x(t), y = y ( t ) y=y(t) y=y(t),
d y d x = d y d t d x d t \frac{d y}{d x}= \frac{\frac{d y}{d t}}{\frac{dx}{dt}} dxdy=dtdxdtdy
三维单参数方程 (一元三维)
x = x ( t ) x=x(t) x=x(t), y = y ( t ) y=y(t) y=y(t), z = z ( t ) z=z(t) z=z(t)
d y d x = d y d t d x d t \frac{d y}{d x}= \frac{\frac{d y}{d t}}{\frac{dx}{dt}} dxdy=dtdxdtdy
d z d x = d z d t d x d t \frac{d z}{d x}= \frac{\frac{d z}{d t}}{\frac{dx}{dt}} dxdz=dtdxdtdz
d z d y = d z d t d y d t \frac{d z}{d y}= \frac{\frac{d z}{d t}}{\frac{dy}{dt}} dydz=dtdydtdz
三维双参数方程 (二元三维)
x = x ( s , t ) x=x(s,t) x=x(s,t), y = y ( s , t ) y=y(s,t) y=y(s,t), z = z ( s , t ) z=z(s,t) z=z(s,t), 求解 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z, ∂ z ∂ y \frac{\partial z}{\partial y} ∂y∂z
推出隐函数 s = s ( x , y ) s=s(x,y) s=s(x,y), t = t ( x , y ) t=t(x,y) t=t(x,y)
z = z ( s , t ) = z ( s ( x , y ) , t ( x , y ) ) z=z(s,t)=z(s(x,y), t(x,y)) z=z(s,t)=z(s(x,y),t(x,y)),
∂ z ∂ x = ∂ z ∂ s ∂ s ∂ x + ∂ z ∂ t ∂ t ∂ x \frac{\partial z}{\partial x}= \frac{\partial z}{\partial s}\frac{\partial s}{\partial x}+ \frac{\partial z}{\partial t}\frac{\partial t}{\partial x} ∂x∂z=∂s∂z∂x∂s+∂t∂z∂x∂t
∂ z ∂ y = ∂ z ∂ s ∂ s ∂ y + ∂ z ∂ t ∂ t ∂ y \frac{\partial z}{\partial y}= \frac{\partial z}{\partial s}\frac{\partial s}{\partial y}+\frac{\partial z}{\partial t}\frac{\partial t}{\partial y} ∂y∂z=∂s∂z∂y∂s+∂t∂z∂y∂t
结合二元二维反函数
记 J = ∂ ( x , y ) ∂ ( s , t ) J=\frac{\partial (x,y)}{\partial (s,t)} J=∂(s,t)∂(x,y)
∂ s ∂ x = 1 J ∂ y ∂ t \frac{\partial s}{\partial x}=\frac{1}{J}\frac{\partial y}{\partial t} ∂x∂s=J1∂t∂y
∂ t ∂ x = − 1 J ∂ y ∂ s \frac{\partial t}{\partial x}=-\frac{1}{J}\frac{\partial y}{\partial s} ∂x∂t=−J1∂s∂y
∂ s ∂ y = − 1 J ∂ x ∂ t \frac{\partial s}{\partial y}=-\frac{1}{J}\frac{\partial x}{\partial t} ∂y∂s=−J1∂t∂x
∂ t ∂ y = 1 J ∂ x ∂ s \frac{\partial t}{\partial y}=\frac{1}{J}\frac{\partial x}{\partial s} ∂y∂t=J1∂s∂x
∂ z ∂ x = 1 J ∂ ( z , x ) ∂ ( s , t ) \frac{\partial z}{\partial x} = \frac{1}{J} \frac{\partial (z,x)}{\partial (s,t)} ∂x∂z=J1∂(s,t)∂(z,x)
∂ z ∂ y = 1 J ∂ ( x , z ) ∂ ( s , t ) \frac{\partial z}{\partial y} = \frac{1}{J} \frac{\partial (x,z)}{\partial (s,t)} ∂y∂z=J1∂(s,t)∂(x,z)
相关文章:
)
【高等数学】多元微分学(二)
隐函数的偏导数 二元方程的隐函数 F ( x , y ) 0 F(x,y)0 F(x,y)0 推出隐函数形式 y y ( x ) yy(x) yy(x). 欲求 d y d x \frac{d y}{d x} dxdy 需要对 F 0 F0 F0 两边同时对 x x x 求全导 0 d d x F ( x , y ( x ) ) ∂ F ∂ x d x d x ∂ F ∂ y d y d x ∂ F…...
和WCF(Windows Communication Foundation))
.NET 中的 Web服务(Web Services)和WCF(Windows Communication Foundation)
一、引言 在当今数字化时代,不同的软件系统和应用程序之间需要进行高效、可靠的通信与数据交换。.NET 框架中的 Web 服务和 WCF(Windows Communication Foundation)为此提供了强大的技术支持。它们在构建分布式应用程序、实现跨平台通信以及…...

Linux小知识2 系统的启动
我们在上文中介绍了文件系统,提到了Linux的文件系统存在一个块的概念,其中有一个特殊的块:引导块。这和我们这里要讲的系统启动有关。 BIOS 基本输入输出系统,基本上是一个操作系统最早实现也是最早运行的第一个程序。是一个比较…...
Oracle-19g数据库的安装
简介 Oracle是一家全球领先的数据库和云解决方案提供商。他们提供了一套完整的技术和产品,包括数据库管理系统、企业级应用程序、人工智能和机器学习工具等。Oracle的数据库管理系统是业界最受欢迎和广泛使用的数据库之一,它可以管理和存储大量结构化和…...
Dubbo快速入门(二):第一个Dubbo程序(附源码)
文章目录 一、生产者工程0.目录结构1.依赖2.配置文件3.启动类4.生产者服务 二、消费者工程0.目录结构1.依赖2.配置文件3.启动类4.服务接口5.controller接口 三、测试代码 本博客配套源码:gitlab仓库 首先,在服务器上部署zookeeper并运行,可以…...

不同数据类型转换与转义的对比差异
(Owed by: 春夜喜雨 http://blog.csdn.net/chunyexiyu) 在C和C语言中,类型转换与转义是有点像的,有时可能被误解,这块需要仔细辨别。 类型转换形如,把不同字节数或相同字节数的类型值进行转换,强调的是数值转换过去&…...
Kylin系统安装VMwareTools工具
如下图所示,安装好Kylin系统之后,还未安装VMwareTools工具,导致系统画面无法填充虚拟机 正常安装了VMwareTools工具后的系统画面 所以,接下来我们介绍一下如何在Kylin系统下安装VMwareTools工具 首先,点击VMware工具栏…...

uni-app 拍照图片添加水印
获取图片信息 uni.chooseImage({count: 6, //默认9sizeType: ["original", "compressed"], //可以指定是原图还是压缩图,默认二者都有sourceType: ["camera"], //从相册选择success: async function (result: any) {if (!props.isMar…...

Docker-registry私有镜像仓库的安装
Docker-registry私有镜像仓库的安装 我在这里的镜像仓库搭建在ip为192.168.3.23的虚机中。 安装docker-registry 1.拉取镜像 # docker pull registry 2.查看镜像 # docker images REPOSITORY TAG IMAGE ID CREATE…...

在vue3中实现祖组件给后代组件传参,可以跨域几层。
使用provide和inject就可以 下面是祖组件代码: //这是祖组件// 引入provide import { provide } from "vue";//定义数据 const projectId ref("");// 给后代组件传参 provide("projectId", projectId); 下面是后代组件代码&#…...

【优选算法】——双指针(上篇)!
🌈个人主页:秋风起,再归来~🔥系列专栏:C刷题算法总结🔖克心守己,律己则安 目录 前言:双指针 1. 移动零(easy) 2. 复写零(easy) 3…...
【C语言】数据输出格式控制
数据的输出格式修饰 常用两种: 整型中,输出数据左对齐、右对齐、占m位、不足m位前补0。浮点型中,默认通过四舍五入保留小数点后6位,通过参数设置保留小数点后n位。 #include <stdio.h> #define PI 3.14159 /* 功能&#x…...

Qt-界面优化选择器的用法(70)
目录 描述 使用 类型选择器 ID 选择器 并集选择器 子控件选择器 伪控制器 描述 QSS 的选择器⽀持以下⼏种 选择器⽰例说明全局选择器*选择所有的 widget.类型选择器 (type selector)QPushButton选择所有的 QPushButton 和其⼦类的控件.类选择器 (class selector).QPus…...
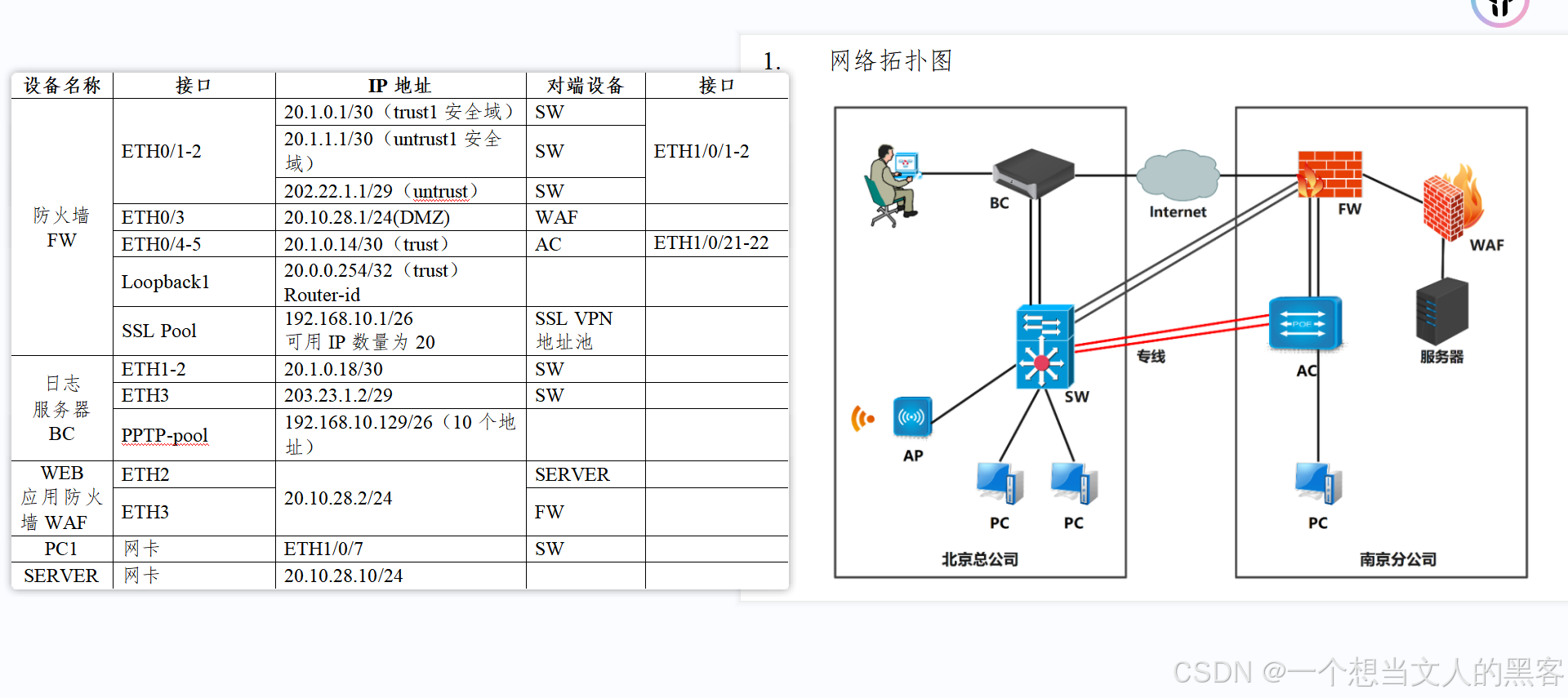
全国职业技能大赛——信息安全管理与评估第一阶段BC、FW、WAF题目详细解析过程
💗需要职业技能大赛环境+WP,请联系我!🍬 博主介绍 👨🎓 博主介绍:大家好,我是 一个想当文人的黑客 ,很高兴认识大家~ ✨主攻领域:【渗透领域】【应急响应】 【edusrc漏洞挖掘】 【VulnHub靶场复现】【面试分析】 🎉欢迎关注💗一起学习👍一起讨论⭐️一起…...
基于Vite创建项目
vite 是新一代前端构建工具,官网地址:https://vitejs.cn,vite的优势如下: 轻量快速的热重载(HMR),能实现极速的服务启动。对 TypeScript、JSX、CSS 等支持开箱即用。真正的按需编译,…...

面试题:在 React 中如何绑定事件
在 React 中绑定事件处理器(event handlers)是一个常见的任务,通常涉及以下几个步骤: 定义一个事件处理器函数:在组件的类或者函数组件内部定义一个处理事件的函数。 在 JSX 中绑定事件处理器:在渲染 JSX 时,使用 on 前缀加上事件名称(如 onClick, onChange, onSubmit …...

前端将JSON或者table直接导出为excel
一、引入Sheetjs或者npm直接下载 <script lang"javascript" src"https://cdn.sheetjs.com/xlsx-0.20.3/package/dist/xlsx.full.min.js"></script> 二、页面中使用 //json导出为excel <button onclick"exportExcel()">导出…...

算法之排序
概述 记录排序算法。 1 选择排序 *** 选择排序* 思路:遍历数组,找出(选择)最小的元素,然后和最左边的元素交换。接下来,再从第二个元素开始遍历整个数组。再找到最小的元素,再和第二个元素交换…...

深度学习:LSTM循环神经网络实现评论情感分析
目录 一、任务介绍 1.任务要求 2.信息内容 3.待思考问题 二、问题解决 1.将评论内容转换成语料库 2.获取每条评论的词向量、标签和长度 3.数据打包 4.建立LSTM循环神经网络模型 1.主程序代码 2.模型代码 5.建立训练集函数和测试集函数 一、任务介绍 1.任务要求 项…...

基于Arduino的环境监测装置
基于Arduino的环境监测装置 引言痛点功能前期准备软件硬件 项目开发硬件开发软件开发 功能演示更多精彩,欢迎关注 引言 本项目使用机智云Gokit2.0开发板,实现基于Arduino的环境监测装置,解决目前大多数人对环境数据要求逐渐增高的痛点。 痛…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...
