买卖股票的最佳时机 题解
买卖股票的最佳时机
问题描述
给定一个数组 prices,其中 prices[i] 表示第 i 天的股票价格。你只能选择某一天买入股票,并选择未来的某一天卖出股票,设计一个算法来计算你所能获取的最大利润。
-
限制条件:
- 只能进行一次交易:也就是说,最多只能买入和卖出各一次。
- 买入必须在卖出之前:不能在买入之前卖出股票。
-
目标:返回可以获得的最大利润。如果无法获取任何利润,返回
0。
示例
-
示例 1:
输入:prices = [7,1,5,3,6,4] 输出:5 解释:在第 2 天(价格为 1)买入,在第 5 天(价格为 6)卖出,利润为 6 - 1 = 5。 -
示例 2:
输入:prices = [7,6,4,3,1] 输出:0 解释:在这种情况下,没有交易完成,所以最大利润为 0。
解题思路
为了求最大利润,我们需要在买入价格最低的时候买入,并在之后价格最高的时候卖出。然而,由于我们只能遍历一次数组,并且需要在买入之后才能卖出,因此我们需要一种高效的方法来计算最大利润。
核心思想:
- 维护一个当前为止的最低买入价格
minPrice。 - 计算当前价格与最低买入价格之间的差值,即当前可获得的利润
price - minPrice。 - 维护一个最大利润值
maxProfit,在遍历过程中更新它。
算法步骤
-
初始化:
minPrice = Infinity:表示当前遇到的最低价格,初始为正无穷大。maxProfit = 0:表示当前计算的最大利润,初始为 0。
-
遍历价格数组:
对于每个价格
price,执行以下操作:-
更新最低价格:
- 如果
price < minPrice,则更新minPrice = price。
- 如果
-
计算当前利润并更新最大利润:
- 计算当前利润
profit = price - minPrice。 - 如果
profit > maxProfit,则更新maxProfit = profit。
- 计算当前利润
-
-
返回结果:
- 遍历完成后,
maxProfit即为所能获得的最大利润。
- 遍历完成后,
代码详解
function maxProfit(prices: number[]): number {let minPrice = Infinity; // 初始化最低价格为无穷大let maxProfit = 0; // 初始化最大利润为 0for (let price of prices) {if (price < minPrice) {minPrice = price; // 更新最低价格} else if (price - minPrice > maxProfit) {maxProfit = price - minPrice; // 更新最大利润}}return maxProfit;
}
-
变量初始化:
minPrice:用于记录当前为止的最低买入价格。maxProfit:用于记录当前为止的最大利润。
-
遍历数组:
for (let price of prices) {... }-
更新最低价格:
if (price < minPrice) {minPrice = price; }- 如果当前价格比之前记录的最低价格还低,更新最低价格。
-
更新最大利润:
else if (price - minPrice > maxProfit) {maxProfit = price - minPrice; }- 如果当前价格与最低价格的差值(利润)大于之前的最大利润,更新最大利润。
-
-
返回结果:
return maxProfit;- 返回计算得到的最大利润。
示例演示
以示例 1 为例,prices = [7,1,5,3,6,4]:
-
初始状态:
minPrice = InfinitymaxProfit = 0
-
遍历过程:
-
price = 7:7 < Infinity,更新minPrice = 7。- 没有更新
maxProfit,因为price - minPrice = 0。
-
price = 1:1 < 7,更新minPrice = 1。- 没有更新
maxProfit,因为price - minPrice = 0。
-
price = 5:5 > 1,计算利润5 - 1 = 4。4 > 0,更新maxProfit = 4。
-
price = 3:3 > 1,计算利润3 - 1 = 2。2 < 4,maxProfit不变。
-
price = 6:6 > 1,计算利润6 - 1 = 5。5 > 4,更新maxProfit = 5。
-
price = 4:4 > 1,计算利润4 - 1 = 3。3 < 5,maxProfit不变。
-
-
结果:
- 最终
maxProfit = 5。
- 最终
时间和空间复杂度分析
-
时间复杂度:O(n),其中 n 是数组
prices的长度。我们只需要遍历一次数组。 -
空间复杂度:O(1),只使用了常数级别的额外空间。
边界情况处理
-
价格单调递减:
- 例如
prices = [7,6,4,3,1],在这种情况下,无法获得正利润。 - 算法会始终更新
minPrice,但maxProfit保持为 0。 - 最终返回 0。
- 例如
-
只有一个价格:
- 当
prices.length == 1时,无法完成交易,利润为 0。
- 当
测试代码
function testMaxProfit() {const testCases = [{ prices: [7, 1, 5, 3, 6, 4], expected: 5 },{ prices: [7, 6, 4, 3, 1], expected: 0 },{ prices: [1, 2], expected: 1 },{ prices: [2, 4, 1], expected: 2 },{ prices: [3], expected: 0 },];for (let { prices, expected } of testCases) {const result = maxProfit(prices);console.assert(result === expected, `测试失败:输入 ${prices},期望输出 ${expected},实际输出 ${result}`);}console.log("所有测试用例通过!");
}testMaxProfit();
总结
- 核心思想:在一次遍历中,找到最低的买入价格和最高的卖出价格(在买入之后)。
- 算法优势:时间复杂度低,只需要遍历一次数组,空间复杂度为 O(1)。
- 注意事项:在更新
minPrice时,只更新更低的价格;在计算利润时,必须确保当前价格是在minPrice之后的。
相关文章:

买卖股票的最佳时机 题解
买卖股票的最佳时机 问题描述 给定一个数组 prices,其中 prices[i] 表示第 i 天的股票价格。你只能选择某一天买入股票,并选择未来的某一天卖出股票,设计一个算法来计算你所能获取的最大利润。 限制条件: 只能进行一次交易&…...

微信小程序路由跳转的区别及其常见的使用场景
在微信小程序中,页面路由跳转的实现有几种常用方式,不同的跳转方式适用于不同的使用场景。下面是几种跳转方法的区别及其在实际项目中的应用场景。 1. wx.navigateTo 简介:保留当前页面并跳转到指定页面,最多保留10个页面的历史记…...
麒麟桌面版v10 SP1以docker方式安装达梦数据库
安装docker 0.切换root用户(可以不切换,但要注意权限问题,我是用root) ymym-pc:~/桌面$ whoami ym ymym-pc:~/桌面$ sudo -i rootym-pc:~# whoami root rootym-pc:~# 1.查看系统版本 [rootlocalhost opt]# cat /etc/os-release…...

KNN的 k 设置的过大会有什么问题
在KNN(K-Nearest Neighbors)算法中,K值的选择对模型的性能和预测结果有着重要影响。如果K值设置得过大,可能会出现以下问题: 欠拟合:当K值过大时,模型会考虑过多的邻近点实例,甚至会…...

Star Tower:智能合约的安全基石与未来引领者
在区块链技术的快速发展中,智能合约作为新兴的应用形式,正逐渐成为区块链领域的重要组成部分。然而,智能合约的可靠性问题一直是用户最为关心的焦点之一。为此,Star Tower以其强大的技术实力和全面的安全保障措施,为智…...
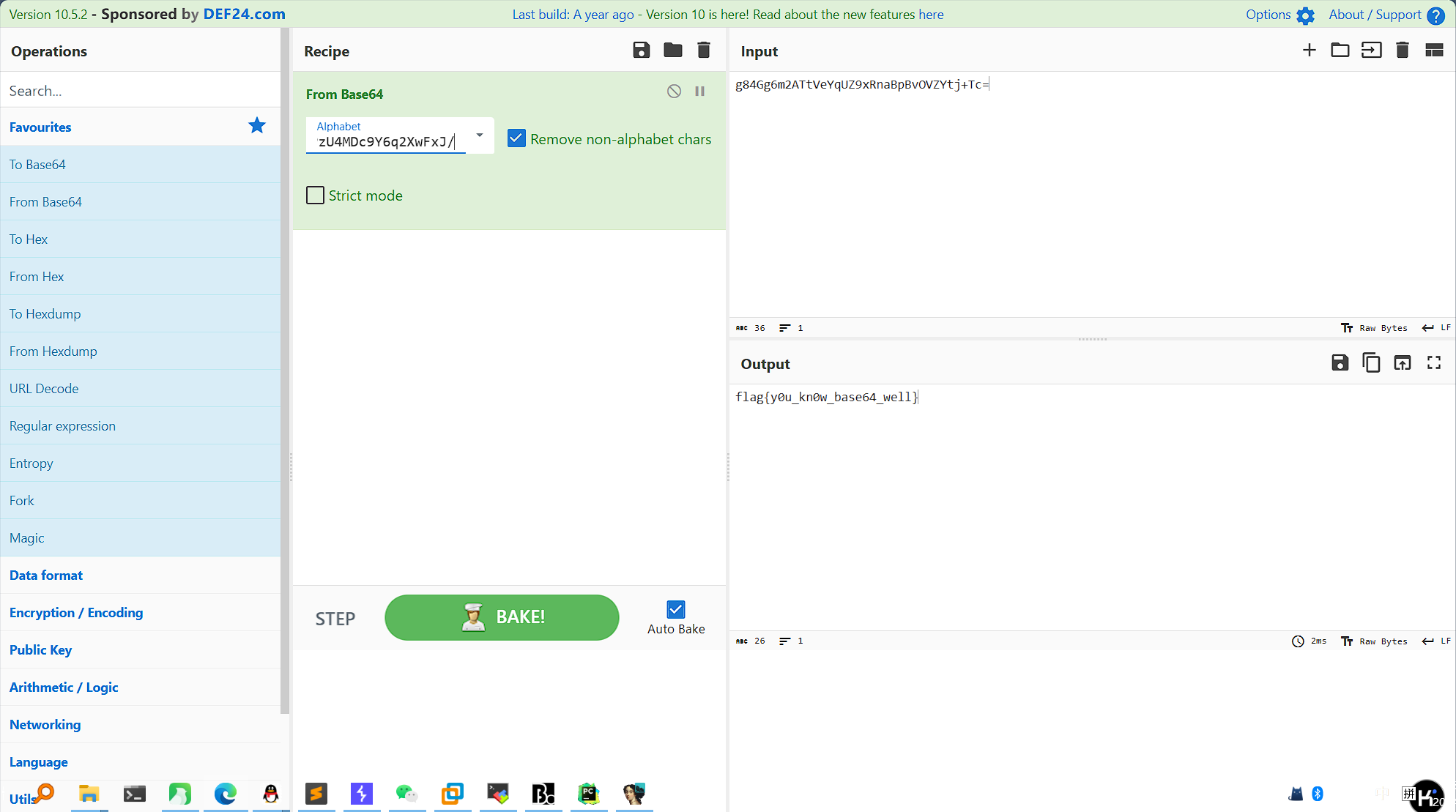
2024-NewStarCTF-WEEK1
web headach3 提示head,抓包查看响应头,得到flag flag值:flag{You_Ar3_R3Ally_A_9ooD_d0ctor} 会赢吗 第一段:源码里找到第一段flag,ZmxhZ3tXQTB3 第二段:分析可知需要在控制台调用revealFlag函数向服务…...

大数据面试题整理——Zookeeper
系列文章目录 大数据面试题专栏点击进入 文章目录 系列文章目录大数据面试题专栏点击进入 1. 什么是 Zookeeper?2. Zookeeper 的特点有哪些?3. Zookeeper 的数据模型是怎样的?4. Zookeeper 的工作流程是怎样的?5. Zookeeper 如何…...

图书库存管理:Spring Boot驱动的进销存系统
1系统概述 1.1 研究背景 随着计算机技术的发展以及计算机网络的逐渐普及,互联网成为人们查找信息的重要场所,二十一世纪是信息的时代,所以信息的管理显得特别重要。因此,使用计算机来管理图书进销存管理系统的相关信息成为必然。开…...
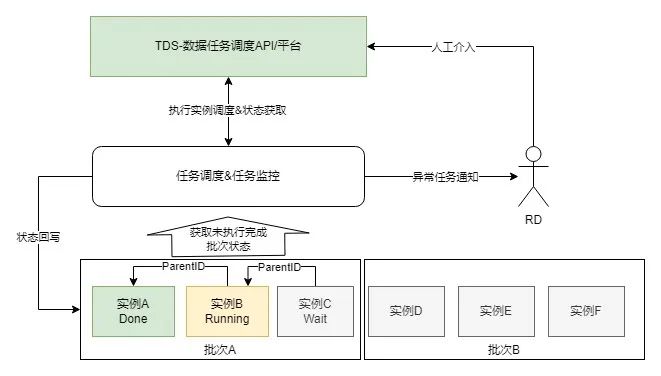
用增结算数仓化改造:在/离线调度系统的构建与应用
导读 移动运营推广平台(OPS)承载着百度内部移动应用/移动搜索业务的用户增长预算的全流程结算线上化管控功能,为了解决用增业务发展规模扩大、原有技术架构老旧、无离线数仓系统等一系列的问题,针对全域结算数据启动了整体的架构…...

施磊C++高级进阶课程 | 学习笔记 | 博客汇总
施磊C高级进阶课程 | 学习笔记 | 博客汇总 施磊C | 进阶学习笔记 | 1.对象的应用优化、右值引用的优化-CSDN博客 施磊C | 进阶学习笔记 | 2.智能指针-CSDN博客 施磊C | 进阶学习笔记 | 3.绑定器和函数对象、lambda表达式-CSDN博客 施磊C | 进阶学习笔记 | 4.c11内容汇总、多…...

学习threejs,拉伸几何体THREE.TubeGeometry管道
👨⚕️ 主页: gis分享者 👨⚕️ 感谢各位大佬 点赞👍 收藏⭐ 留言📝 加关注✅! 👨⚕️ 收录于专栏:threejs gis工程师 文章目录 一、🍀前言1.1 ☘️拉伸几何体THREE.TubeGeome…...

day01-Qt5入门
day01-Qt5入门 窗体应用 1.1 窗体基类说明 创建项目在details中编辑器提供了三个基类,分别是 QMainWindows、Qwidget、QDialog 1、 QMainWindow QMainWindow 类提供一个有菜单条、锚接窗口(例如工具条)和一个状态条的主应用 程序窗口。…...

AnaTraf | 利用多点关联数据分析和网络关键KPI监控提升IT运维效率
目录 什么是多点关联数据分析? 多点关联数据分析的运用场景 监控网络关键KPI的重要性 典型的网络关键KPI 案例分析:利用多点关联数据分析和KPI监控解决网络性能问题 结语 AnaTraf 网络性能监控系统NPM | 全流量回溯分析 | 网络故障排除工具AnaTraf…...

图书库存控制:Spring Boot进销存系统的应用
2相关技术 2.1 MYSQL数据库 MySQL是一个真正的多用户、多线程SQL数据库服务器。 是基于SQL的客户/服务器模式的关系数据库管理系统,它的有点有有功能强大、使用简单、管理方便、安全可靠性高、运行速度快、多线程、跨平台性、完全网络化、稳定性等,非常…...

Python 工具库每日推荐 【pyspider 】
文章目录 引言网络爬虫的重要性今日推荐:pyspider 网络爬虫框架主要功能:使用场景:安装与配置快速上手示例代码代码解释实际应用案例案例:爬取新闻网站的文章案例分析高级特性使用代理处理 JavaScript 渲染的页面扩展阅读与资源优缺点分析优点:缺点:总结【 已更新完 Type…...
网络编程 - <sys/socket.h> 和 <netinet/in.h>)
【C语言教程】【常用类库】(十五)网络编程 - <sys/socket.h> 和 <netinet/in.h>
15. 网络编程 - <sys/socket.h> 和 <netinet/in.h> 网络编程在C语言中是通过套接字来实现的,套接字提供了进程间通信的端点。C语言的网络编程涉及到创建套接字、绑定地址、监听和接收数据。以下是网络编程的关键概念和基本实现方法。 15.1. 套接字基础…...

正点原子讲解SPI学习,驱动编程NOR FLASH实战
配置SPI传输速度时,需要先失能SPI,__HAL_SPI_DISABLE,然后操作SPI_CR1中的波特率设置位,再使能SPI, NM25Q128驱动步骤 myspi.c #include "./BSP/MYSPI/myspi.h"SPI_HandleTypeDef g_spi1_handler; /* SPI句柄 */void spi1_init(void) {g_spi…...

低代码开发助力中小企业数字化转型难度持续降低
随着信息技术的飞速发展,数字化转型已成为企业持续发展的关键驱动力。对于中小企业而言,数字化转型不仅意味着提升效率、降低成本,更是实现业务模式创新和市场竞争力提升的重要途径。然而,传统软件开发模式的高成本、长周期和复杂…...

【Linux】:线程控制
朋友们、伙计们,我们又见面了,本期来给大家带来线程控制相关代码和知识点,如果看完之后对你有一定的启发,那么请留下你的三连,祝大家心想事成! C 语 言 专 栏:C语言:从入门到精通 数…...

大数据-174 Elasticsearch Query DSL - 全文检索 full-text query 匹配、短语、多字段 详细操作
点一下关注吧!!!非常感谢!!持续更新!!! 目前已经更新到了: Hadoop(已更完)HDFS(已更完)MapReduce(已更完&am…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...
