【算法篇】动态规划类(2)——01背包+完全背包(笔记)
目录
一、理论基础
1. 问题类型
2. 01背包问题
3. 完全背包问题
4. 解题步骤
(1)确定dp数组(dp table)以及下标的含义。
(2)确定递推公式。
(3)dp数组如何初始化。
(4)确定遍历顺序。
(5)举例推导dp数组。
二、Leetcode 题目
1. 分割等和子集
2. 最后一块石头的重量II
3. 目标和
4. 一和零
5. 零钱兑换II
6. 组合总和 Ⅳ
7. 零钱兑换
8. 完全平方数
9. 单词拆分
三、总结
1. 01背包问题
2. 完全背包问题
一、理论基础
1. 问题类型


2. 01背包问题


使用二维数组,其中有两个维度需要分别表示:物品 和 背包容量。
这里 i 来表示物品、j 表示背包容量。(如果想用 j 表示物品,j 表示背包容量都可以的)
改进:如果把 dp[i - 1] 那一层拷贝到 dp[i] 上,表达式完全可以是:dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]); 与其把 dp[i - 1] 这一层拷贝到 dp[i] 上,不如只用一个一维数组了,只用 dp[j](一维数组,也可以理解是一个滚动数组)。
3. 完全背包问题
完全背包 和 01背包问题 唯一不同的地方就是,每种物品有无限件。
- 如果求组合数就是外层 for 循环遍历物品,内层 for 遍历背包。
- 如果求排列数就是外层 for 遍历背包,内层 for 循环遍历物品。
4. 解题步骤
(1)确定dp数组(dp table)以及下标的含义。
(2)确定递推公式。
(3)dp数组如何初始化。
(4)确定遍历顺序。
(5)举例推导dp数组。
二、Leetcode 题目
1. 分割等和子集
https://leetcode.cn/problems/partition-equal-subset-sum/description/![]() https://leetcode.cn/problems/partition-equal-subset-sum/description/
https://leetcode.cn/problems/partition-equal-subset-sum/description/
给你一个 只包含正整数 的 非空 数组
nums。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
示例 1:
输入:nums = [1,5,11,5]
输出:true
解释:数组可以分割成 [1, 5, 5] 和 [11] 。示例 2:
输入:nums = [1,2,3,5]
输出:false
解释:数组不能分割成两个元素和相等的子集。理解:
① dp[j] 表示 背包总容量(所能装的总重量)是 j,放进物品后,背的最大重量为 dp[j]。那么如果背包容量为 target, dp[target] 就是装满 背包之后的重量,所以 当 dp[target] == target 的时候,背包就装满了。
② 递推公式为:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); 本题,相当于背包里放入数值,那么 物品 i 的 重量是 nums[i],其价值也是 nums[i]。
③ dp[0] 一定是 0。
class Solution {
public:bool canPartition(vector<int>& nums) {int sum = 0;for (int i = 0; i < nums.size(); i++) {sum += nums[i];}if (sum % 2 == 1) return false;int target = sum / 2;vector<int> dp(10001, 0);for (int i = 0; i < nums.size(); i++) {for (int j = target; j >= nums[i]; j--) {dp[j] = max(dp[j], nums[i] + dp[j - nums[i]]);}}if (dp[target] == target) return true;return false;}
};
2. 最后一块石头的重量II
https://leetcode.cn/problems/last-stone-weight-ii/description/![]() https://leetcode.cn/problems/last-stone-weight-ii/description/
https://leetcode.cn/problems/last-stone-weight-ii/description/
有一堆石头,用整数数组
stones表示。其中stones[i]表示第i块石头的重量。每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为
x和y,且x <= y。那么粉碎的可能结果如下:
- 如果
x == y,那么两块石头都会被完全粉碎;- 如果
x != y,那么重量为x的石头将会完全粉碎,而重量为y的石头新重量为y-x。最后,最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下,就返回
0。
示例 1:
输入:stones = [2,7,4,1,8,1]
输出:1
解释:
组合 2 和 4,得到 2,所以数组转化为 [2,7,1,8,1],
组合 7 和 8,得到 1,所以数组转化为 [2,1,1,1],
组合 2 和 1,得到 1,所以数组转化为 [1,1,1],
组合 1 和 1,得到 0,所以数组转化为 [1],这就是最优值。示例 2:
输入:stones = [31,26,33,21,40]
输出:5理解:
① 本题中,石头的重量是 stones[i],石头的价值也是 stones[i] ,可以 “最多可以装的价值为 dp[j]” == “最多可以背的重量为dp[j]”
② 本题为:dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);
③ 提示中给出 1 <= stones.length <= 30,1 <= stones[i] <= 100,所以最大重量就是 30 * 100 。所以 dp 数组开到 1500 大小就可以了。
class Solution {
public:int lastStoneWeightII(vector<int>& stones) {vector<int> dp(3001, 0);int sum = 0;for (int i = 0; i < stones.size(); i++) {sum += stones[i];}int target = sum / 2; // 将石头分成两堆,计算两堆的最小差for (int i = 0; i < stones.size(); i++) {for (int j = target; j >= stones[i]; j--) {dp[j] = max(dp[j], stones[i] + dp[j - stones[i]]);}}return sum - dp[target] - dp[target];}
};
3. 目标和
https://leetcode.cn/problems/target-sum/description/![]() https://leetcode.cn/problems/target-sum/description/
https://leetcode.cn/problems/target-sum/description/
给你一个非负整数数组
nums和一个整数target。向数组中的每个整数前添加'+'或'-',然后串联起所有整数,可以构造一个 表达式 :
- 例如,
nums = [2, 1],可以在2之前添加'+',在1之前添加'-',然后串联起来得到表达式"+2-1"。返回可以通过上述方法构造的、运算结果等于
target的不同 表达式 的数目。
示例 1:
输入:nums = [1,1,1,1,1], target = 3
输出:5
解释:一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3示例 2:
输入:nums = [1], target = 1
输出:1理解:
① dp[i][j]:使用 下标为 [0, i] 的 nums[i] 能够凑满 j(包括 j)这么大容量的包,有 dp[i][j] 种方法。
② 本题中,物品i的容量是 nums[i],价值也是 nums[i]。
不放物品 i:即背包容量为 j,里面不放 物品 i,装满有 dp[i - 1][j] 中方法。
放物品 i: 即:先空出物品i的容量,背包容量为( j - 物品 i 容量),放满背包有 dp[i - 1][j - 物品i容量] 种方法。
递推公式:dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i]];
class Solution {
public:int findTargetSumWays(vector<int>& nums, int target) {int sum = 0;for (int i = 0; i < nums.size(); i++) {sum += nums[i];}if (abs(target) > sum || (target + sum) % 2 == 1) return 0;int bagsum = (target + sum) / 2;vector<int> dp(bagsum + 1, 0);dp[0] = 1;for (int i = 0; i < nums.size(); i++) {for (int j = bagsum; j >= nums[i]; j--) {dp[j] += dp[j - nums[i]];}}return dp[bagsum];}
};
4. 一和零
https://leetcode.cn/problems/ones-and-zeroes/description/![]() https://leetcode.cn/problems/ones-and-zeroes/description/
https://leetcode.cn/problems/ones-and-zeroes/description/
给你一个二进制字符串数组
strs和两个整数m和n。请你找出并返回strs的最大子集的长度,该子集中 最多 有m个0和n个1。如果x的所有元素也是y的元素,集合x是集合y的 子集 。
示例 1:
输入:strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
输出:4
解释:最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ,因此答案是 4 。
其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意,因为它含 4 个 1 ,大于 n 的值 3 。示例 2:
输入:strs = ["10", "0", "1"], m = 1, n = 1
输出:2
解释:最大的子集是 {"0", "1"} ,所以答案是 2 。理解:
① dp[i][j]:最多有 i 个 0 和 j 个 1 的 strs 的最大子集的大小为 dp[i][j]。
② dp[i][j] 可以由前一个 strs 里的字符串推导出来,strs 里的字符串有 zeroNum 个 0,oneNum 个 1。dp[i][j] 就可以是 dp[i - zeroNum][j - oneNum] + 1。然后我们在遍历的过程中,取 dp[i][j] 的最大值。
所以递推公式:dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
③ dp 数组初始化为 0
class Solution {
public:int findMaxForm(vector<string>& strs, int m, int n) {// 多重背包问题(m:0. n:1)vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));for (string str: strs) {int oneNum = 0, zeroNum = 0;for (int i = 0; i < str.size(); i++) {if (str[i] == '0') zeroNum++;else oneNum++;}for (int i = m; i >= zeroNum; i--) {for (int j = n; j >= oneNum; j--) {dp[i][j] = max(dp[i][j], 1 + dp[i - zeroNum][j - oneNum]);}}}return dp[m][n];}
};
5. 零钱兑换II
https://leetcode.cn/problems/coin-change-ii/description/![]() https://leetcode.cn/problems/coin-change-ii/description/
https://leetcode.cn/problems/coin-change-ii/description/
给你一个整数数组
coins表示不同面额的硬币,另给一个整数amount表示总金额。请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回
0。假设每一种面额的硬币有无限个。
题目数据保证结果符合 32 位带符号整数。
示例 1:
输入:amount = 5, coins = [1, 2, 5]
输出:4
解释:有四种方式可以凑成总金额:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1示例 2:
输入:amount = 3, coins = [2]
输出:0
解释:只用面额 2 的硬币不能凑成总金额 3 。示例 3:
输入:amount = 10, coins = [10]
输出:1理解:
① dp[j]:凑成总金额j的货币组合数为 dp[j]。
② dp[j] 就是所有的 dp[j - coins[i]](考虑 coins[i] 的情况)相加。所以递推公式:dp[j] += dp[j - coins[i]];
③ dp[0] 一定要为 1。
class Solution {
public:int change(int amount, vector<int>& coins) {vector<int> dp(amount + 1, 0);dp[0] = 1;for (int i = 0; i < coins.size(); i++) { // 遍历物品for (int j = coins[i]; j <= amount; j++) { // 遍历背包if (dp[j] < INT_MAX - dp[j - coins[i]]) {dp[j] += dp[j - coins[i]];}}}return dp[amount];}
};
6. 组合总和 Ⅳ
https://leetcode.cn/problems/combination-sum-iv/description/![]() https://leetcode.cn/problems/combination-sum-iv/description/
https://leetcode.cn/problems/combination-sum-iv/description/
给你一个由 不同 整数组成的数组
nums,和一个目标整数target。请你从nums中找出并返回总和为target的元素组合的个数。题目数据保证答案符合 32 位整数范围。
示例 1:
输入:nums = [1,2,3], target = 4
输出:7
解释:
所有可能的组合为:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
请注意,顺序不同的序列被视作不同的组合。示例 2:
输入:nums = [9], target = 3
输出:0理解:
① dp[i]: 凑成目标正整数为i的排列个数为 dp[i]
② dp[i](考虑 nums[j])可以由 dp[i - nums[j]](不考虑 nums[j]) 推导出来。因为只要得到 nums[j],排列个数 dp[i - nums[j]],就是 dp[i] 的一部分。
③ 因为递推公式 dp[i] += dp[i - nums[j]] 的缘故,dp[0] 要初始化为 1。
class Solution {
public:int combinationSum4(vector<int>& nums, int target) {vector<int> dp(target + 1, 0);dp[0] = 1;for (int i = 0; i <= target; i++) {for (int j = 0; j < nums.size(); j++) {if (i - nums[j] >= 0 && dp[i] < INT_MAX - dp[i - nums[j]]) {dp[i] += dp[i - nums[j]];}}}return dp[target];}
};
7. 零钱兑换
https://leetcode.cn/problems/coin-change/description/![]() https://leetcode.cn/problems/coin-change/description/
https://leetcode.cn/problems/coin-change/description/
给你一个整数数组
coins,表示不同面额的硬币;以及一个整数amount,表示总金额。计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回
-1。你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1示例 2:
输入:coins = [2], amount = 3
输出:-1示例 3:
输入:coins = [1], amount = 0
输出:0理解:
① dp[j]:凑足总额为 j 所需钱币的最少个数为 dp[j]
② 凑足总额为 j - coins[i] 的最少个数为 dp[j - coins[i]],那么只需要加上一个钱币coins[i] 即 dp[j - coins[i]] + 1就是 dp[j](考虑 coins[i])所以 dp[j] 要取所有 dp[j - coins[i]] + 1 中最小的。
递推公式:dp[j] = min(dp[j - coins[i]] + 1, dp[j]);
③ 凑足总金额为 0 所需钱币的个数一定是 0,那么 dp[0] = 0;
// 写法一:(背包在外层循环)
class Solution {
public:int coinChange(vector<int>& coins, int amount) {vector<int> dp(amount + 1, INT_MAX);dp[0] = 0; // 0 可以被 0 填充for (int i = 1; i <= amount; i++) {for (int j = 0; j < coins.size(); j++) {if (i - coins[j] >= 0 && dp[i - coins[j]] != INT_MAX) {dp[i] = min(dp[i - coins[j]] + 1, dp[i]);}}}if (dp[amount] == INT_MAX) return -1;return dp[amount];}
};// 写法二:(物品在外层循环)
class Solution {
public:int coinChange(vector<int>& coins, int amount) {vector<int> dp(amount + 1, INT_MAX);dp[0] = 0; // 0 可以被 0 填充for (int i = 0; i < coins.size(); i++) {for (int j = coins[i]; j <= amount; j++) {if (dp[j - coins[i]] != INT_MAX) {dp[j] = min(dp[j], dp[j - coins[i]] + 1);}}}if (dp[amount] == INT_MAX) return -1;return dp[amount];}
};
8. 完全平方数
https://leetcode.cn/problems/perfect-squares/description/![]() https://leetcode.cn/problems/perfect-squares/description/
https://leetcode.cn/problems/perfect-squares/description/
给你一个整数
n,返回 和为n的完全平方数的最少数量 。完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,
1、4、9和16都是完全平方数,而3和11不是。
示例 1:
输入:n = 12
输出:3
解释:12 = 4 + 4 + 4示例 2:
输入:n = 13
输出:2
解释:13 = 4 + 9理解:
① dp[j]:和为 j 的完全平方数的最少数量为 dp[j]。
② dp[j] 可以由 dp[j - i * i] 推出, dp[j - i * i] + 1 便可以凑成 dp[j]。此时我们要 选择最小的 dp[j],所以递推公式:dp[j] = min(dp[j - i * i] + 1, dp[j]);
③ dp[0] 表示 和为 0 的完全平方数的 最小数量,那么 dp[0] 一定是 0。非 0 下标的 dp[j]一定要初始为最大值,这样 dp[j] 在递推的时候才不会被初始值覆盖。
// 写法一:(现遍历背包)
class Solution {
public:int numSquares(int n) {vector<int> dp(n + 1, INT_MAX);dp[0] = 0;for (int i = 0; i <= n; i++) { // 遍历背包for (int j = 1; j * j <= i; j++) { // 遍历物品dp[i] = min(dp[i], dp[i - j * j] + 1);}}return dp[n];}
};// 写法二:(现遍历物品)
class Solution {
public:int numSquares(int n) {vector<int> dp(n + 1, INT_MAX);dp[0] = 0;for (int i = 1; i * i <= n; i++) { // 遍历物品for (int j = i * i; j <= n; j++) { // 遍历背包dp[j] = min(dp[j - i * i] + 1, dp[j]);}}return dp[n];}
};
9. 单词拆分
https://leetcode.cn/problems/word-break/description/![]() https://leetcode.cn/problems/word-break/description/
https://leetcode.cn/problems/word-break/description/
给你一个字符串
s和一个字符串列表wordDict作为字典。如果可以利用字典中出现的一个或多个单词拼接出s则返回true。注意:不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。
示例 1:
输入: s = "leetcode", wordDict = ["leet", "code"]
输出: true
解释: 返回 true 因为 "leetcode" 可以由 "leet" 和 "code" 拼接成。示例 2:
输入: s = "applepenapple", wordDict = ["apple", "pen"]
输出: true
解释: 返回 true 因为 "applepenapple" 可以由 "apple" "pen" "apple" 拼接成。注意,你可以重复使用字典中的单词。示例 3:
输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
输出: false理解:
① dp[i] : 字符串长度为 i 的话,dp[i] 为 true,表示可以拆分为 一个或多个 在字典中出现的单词。
② 如果确定 dp[j] 是 true,且 [j, i] 这个区间的子串出现在字典里,那么 dp[i] 一定是true。( j < i )。所以递推公式是 if([j, i] 这个区间的子串出现在字典里 && dp[j] 是 true) 那么 dp[i] = true。
③ dp[i] 的状态依靠 dp[j] 是否为 true,那么 dp[0] 就是递推的根基,dp[0] 一定要为true。
class Solution {
public:bool wordBreak(string s, vector<string>& wordDict) {unordered_set<string> wordSet(wordDict.begin(), wordDict.end());vector<bool> dp(s.size() + 1, false);dp[0] = true;for (int i = 1; i <= s.size(); i++) { // 遍历背包for (int j = 0; j < i; j++) { // 遍历物品string word = s.substr(j, i - j); // 从 j 开始的 i-j 个字符if (wordSet.find(word) != wordSet.end() && dp[j]) {dp[i] = true;}}}return dp[s.size()];}
};
三、总结
1. 01背包问题

2. 完全背包问题

相关文章:

【算法篇】动态规划类(2)——01背包+完全背包(笔记)
目录 一、理论基础 1. 问题类型 2. 01背包问题 3. 完全背包问题 4. 解题步骤 (1)确定dp数组(dp table)以及下标的含义。 (2)确定递推公式。 (3)dp数组如何初始化。 &#x…...

基于SpringBoot的“社区医院管理服务系统”的设计与实现(源码+数据库+文档+PPT)
基于SpringBoot的“社区医院管理服务系统”的设计与实现(源码数据库文档PPT) 开发语言:Java 数据库:MySQL 技术:SpringBoot 工具:IDEA/Ecilpse、Navicat、Maven 系统展示 系统首页界面图 用户注册界面图 医生界面…...

二进制漏洞利用 | 整数溢出探究
什么是整数溢出? 整数溢出是指当算术运算的结果超出用于存储该结果的数据类型的容量时发生的现象。简单来说,就是当一个数值变得过大(对于有符号整数来说,也可能是过小),无法被正常存储,从而导…...

10种经典的螺栓防松设计
螺栓防松在机械设计中至关重要,不同方式的螺栓防松有哪些特点一起来看一下。 01双螺母 双螺母防松也称对顶螺母防松,当两个对顶螺母拧紧后,两个对顶的螺母之间始终存在相互作用的压力,两螺母中有任何一个要转动都需要克服旋合螺纹…...

开放式蓝牙耳机哪个品牌好用?开放式耳机排行榜测评!
开放式耳机,因其特殊的不入耳佩戴模式,让使用者在享受音乐或者进行通话的过程中,依然可以对外界声音保持敏感。在户外运动场景下,这种特性优势尽显,既保证了耳机佩戴的稳定和舒适,又提高了运动的安全性。为…...

新能源行业必会基础知识---电力现货问答---第5问---何为电力中长期市场?与电力现货市场之间有何关系?国内试点地区如何衔接?国外有哪些经验值得借鉴?
新能源行业必会基础知识-----电力现货问答-----主目录-----持续更新https://blog.csdn.net/grd_java/article/details/142909208 虽然这本书已经出来有几年了,现货市场已经产生了一定变化,但是原理还是相通的。还是推荐大家买来这本书进行阅读观看&#…...

如何将数据从 AWS S3 导入到 Elastic Cloud - 第 2 部分:Elastic Agent
作者:来自 Elastic Hemendra Singh Lodhi 了解将数据从 AWS S3 提取到 Elastic Cloud 的不同选项。 这是多部分博客系列的第二部分,探讨了将数据从 AWS S3 提取到 Elastic Cloud 的不同选项。 在本博客中,我们将了解如何使用 Elastic Agent…...

DTL698电表数据 转 profinet IO协议项目案例
目录 1 案例说明 1 2 VFBOX网关工作原理 1 3 准备工作 2 4 配置VFBOX网关 2 5 用PROFINET IO协议转发数据 4 6 其他说明 6 7 案例总结 7 1 案例说明 设置网关采集DLT698电表数据数据把采集的数据转成profinet IO协议转发给其他系统。 2 VFBOX网关工作原理 VFBOX网关是协议转…...

CSS @规则(At-rules)系列详解___@font-face规则使用方法
CSS 规则(At-rules)系列详解 ___font-face规则使用方法 本文目录: 零、时光宝盒 一、CSSfont-face规则定义和用法 二、font-face语法 三、font-face使用方法例子 3.1、指定一种字体 3.2、font-face 里添加文本的描述符 3.3、设置多个 font-face 规则。 3.4…...

如何通过CDN优化网站服务器访问速度?
CDN,即内容分发网络(Content Delivery Network),在现代互联网中起着重要作用。它可以显著提升网站服务器的访问速度。以下是CDN在加速网站访问方面的主要优势及其工作原理。 1. 全球分布的服务器节点 CDN通过在全球范围内布设多个…...

JAVA学习-练习试用Java实现“自定义函数之字符反转”
问题: 写一函数,使输入的一个字符串按反序存放,在主函数中输入并输出反序后的字符串(不包含空格)。 示例 :输入一行字符123456abcdef,输出逆序后的字符串fedcba654321。 解答思路: …...

大衍数列——考研408考试科目之数据算法——未来之窗学习通
一、大衍数列 中国古代文献中,曾记载过“大衍数列”, 主要用于解释中国传统文化中的太极衍生原理。 它的前几项是:0、2、4、8、12、18、24、32、40、50 … 其规律是:对偶数项,是序号平方再除2,奇数项,是…...

JVM(HotSpot):直接内存及其使用建议
文章目录 一、什么是直接内存?二、特点三、使用案例四、直接内存的管理 一、什么是直接内存? Direct Memory:系统内存 普通IO,运行原理图 磁盘到系统内存,系统内存到jvm内存。 NIO,运行原理图 划分了一块…...

centos7安装mysql5.7
1. 更新系统软件包 首先,确保您的系统是最新的。打开终端并运行: sudo yum update -y 2. 安装MySQL 5.7的YUM仓库 MySQL提供了自己的YUM仓库,您可以通过下载并安装官方提供的RPM包来添加这个仓库。 wget https://dev.mysql.com/get/mysql57-c…...
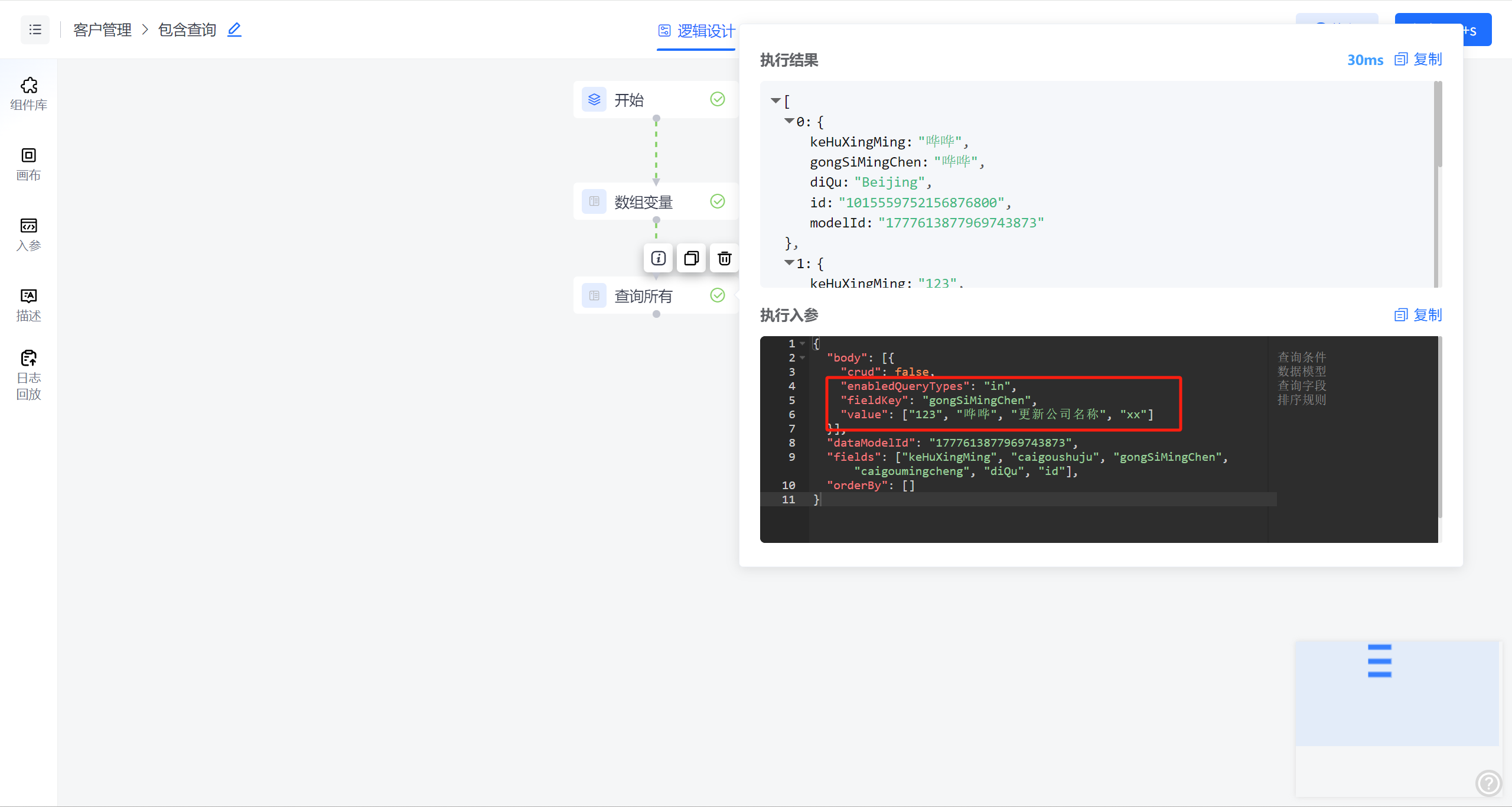
如何在JVS逻辑引擎中巧妙运用包含查询功能?
在实际业务场景中,数据查询是不可或缺的一环,包含查询在实际业务场景中经常用到,被广泛应用于各类业务系统中。当我们需要查询状态为指定几种状态的数据时,类似SQL语句中的IN查询就显得尤为重要。为了满足这一需求,在J…...

Spring Boot视频网站:安全与可扩展性设计
4 系统设计 4.1系统概要设计 视频网站系统并没有使用C/S结构,而是基于网络浏览器的方式去访问服务器,进而获取需要的数据信息,这种依靠浏览器进行数据访问的模式就是现在用得比较广泛的适用于广域网并且没有网速限制要求的B/S结构,…...

深入理解 Flutter 鸿蒙版的 Stack 布局:适配屏幕与层叠样式布局
目录 写在前面 什么是 Stack 布局? Stack 的基本用法 Stack 布局的核心概念 屏幕适配与 Stack 布局 使用 MediaQuery 获取屏幕尺寸 使用 LayoutBuilder 进行自适应布局 高级层叠样式布局示例 1. 照片展示与文字描述 2. 动态调整层叠布局 写在最后 写在前…...

JavaScript中Number相关特性
目录 非 VIP 用户可前往公众号“前端基地”进行免费阅读 数值范围 小数注意问题 NaN isNaN()判断是不是NaN JavaScript可以表示的进制 数值扩展 非 VIP 用户可前往公众号“前端基地”进行免费阅读 数值范围 数字类型主要涵盖整数与小数。在数值范围方面,存在特…...

Redis中String类型数据扩容原理分析
大家好,我是 V 哥。在 Java 中,我们有动态数组ArrayList,当插入新元素空间不足时,会进行扩容,好奇 Redis 中的 String 类型,C 语言又是怎样的实现策略,带着疑问,咱们来了解一下。 最…...

智能码二维码zhinengma.cn在供应链管理中有哪些优势?
智能码二维码在供应链管理中具有以下优势: 一、提高信息透明度 通过为每个产品或包装分配唯一的二维码,可以实现供应链各环节信息的实时共享。这有助于提高供应链的信息透明度,让各方都能及时了解产品的状态和位置。 二、加强追溯能力 智…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...
