【数据结构与算法】线性表顺序存储结构
文章目录
- 一.顺序表的存储结构定义
- 1.1定义
- 1.2 图示
- 1.3结构代码
- *C语言的内存动态分配
- 二.顺序表基本运算
- *参数传递
- 2.1建立
- 2.2初始化(InitList(&L))
- 2.3销毁(DestroyList(&L))
- 2.4判断线性表是否为空表(ListEmpty(L))
- 2.5求线性表的长度(ListLength(L))
- 2.6输出线性表(DispList(L))
- 2.7查找元素的操作(GetElem与LocateElem)
- 2.7.1按序号(GetElem(L,i,&e))
- 2.7.2按元素(LocateElem(L,e))
- 2.8插入数据元素(ListInsert(&L,i,e))
- 2.9删除数据元素(ListDelet(&L,i,&e))
- 三.顺序表优缺点
一.顺序表的存储结构定义
1.1定义
线性表的顺序表示又称为顺序存储结构或顺序映像,称为顺序表,其逻辑结构与存储结构一致:用一段地址连续的存储单元依次存储线性表的数据元素。
设顺序表的每个元素占用
c个存储单元,则第i个元素的存储地址为:所以,只要确定了存储顺序表的起始地址(即基地址```a1```),计算任意一个元素的存储地址的时间是相等的。
1.2 图示

如图可见顺序表的特点:地址连续,依次存放,随机存取和类型相同(即以物理位置相邻表示逻辑关系,任一元素均可随机存取),我们通常用一维数组表示顺序表,也就是把线性表中相邻元素存储在数组中相邻位置,从而导致数据元素的序号和存放它的数组下标之间具有一一对应的关系。
注意:
C语言中数组的下标是从0开始的,而顺序表中元素的序号是从1开始的,即线性表中第i个元素存储在数组中下标为i-1的位置。
1.3结构代码
#define LIST INIT SIZE 100 //线性表存储空间的初始分配量
typedef struct{ElemType elem[LIST_INIT_SIZE];//存放顺序表中的元素的一个数组,可以替换,事先定义int length; //当前长度
}SqList; //SqList是存放ElemType类型元素的顺序表,指针指向第一个元素的地址
从上面代码我们可以看到,这里我们封装了一个结构,事实上就是对数组进行封装,增加了个当前长度的变量罢了。(通过sqlist这个结构对数组进行封装,多了一个length的变量)
总结一下:顺序存储结构封装需要三个属性。
- 存储空间的起始位置,数组data,它的存储位置就是线性表存储空间的存储位置。(类似队伍的第一个同学找到自己的位置)
- 线性表的最大存储容量,数组长度maxsize(也就是我们总共买了多少张票)
- data三个含义:首地址,地址常量,&data[0]
- 线性表的当前长度:length(也就是总共来了多少人)
注意:数组的长度与线性表的当前长度需要区分一下:数组的长度是存放线性表的存储空间的总长度,一般初始化后不变。而线性表的当前长度是线性表中元素的个数,是会变化的。由于线性表中可以进行插入操作,所以数组长度要大于当前线性表的长度。
*C语言的内存动态分配
由上诉内容可知,[MaxSize]是固定的,存放地址也固定,下面我们介绍动态内存分配,可以重建或修改数组
- 获得这个根数组中基地址(第一个元素的地址),其他地址用下标来操作。
//先定义指针,用内存分配函数,动态分配内存定义空间
typedef struct{ElemType *elem;int length;
}SqList;//顺序表类型
L.elem=(ElemType*)malloc(sizeof(ElemType)*MAXSIZE);//分配MaxSize个ElemType类型的空间
//返回值类型是void*,所以要强转
//要保存这个地址到data中就要把malloc返回值强转为L.data的类型
二.顺序表基本运算
*参数传递
在学习顺序表基本运算之前,我们先了解一下相关的知识点——C++中的参数传递
-
函数调用时传送给形参表的实参必须与形参三个一致:类型,个数,顺序
-
参数传递有两种方式:传值方式(参数为整型,实型和字符型等)和传地址
-
传地址有三种:参数为指针变量,参数为引用类型,参数为数组名
注意:当指针变量做参数时,形参变化不影响实参(栈的创建和销毁)
#include<iostream.h> void swap(float *m,float *n){float *t;t=m;m=n;n=t; } void main(){float a,b,*p1,*p2;cin>>a>>b;p1=&a;p2=&b;//即交换p1和p2的值不会影响a和b的值swap(p1,p2); } cout<<a<<endl<<b<<endl;-
数组名作参数
-
数组可以看成const指针(特殊的指针),定义后不可修改
-
传递的是数组的首地址
-
对形参数组所做的任何改变都将反映到实参数组中
-
//用数组做函数的参数,求10个整数的最大数 #include<iostream.h> #define N 10//定义常量N为10 int max(int b[]){//定义计算数组中最大数的函数int i,n;n=b[0];for(i=1;i<N;i++)if(n<b[i])n=b[i];return n; } int max(int a[]); void main(){int a[10];int i,m;for(i=0;i<N;i++)cin>>a[i];m=max(a);cout<<"the max number is:"<<m; }-
引用类型做参数
-
引用,它用来给一个对象提供一个替代的名字
-
传递引用参数给函数与传递指针的效果是一样的,形参变化实参也发生变化。
引用类型做形参,在内存中并没有产生实参的副本,它直接对实参操作;而一般变量做参数,形参与实参就占用不同的存储单元,所以形参变量的值是实参变量的副本。因此,当参数传递的数据量较大时,用引用比用一般变量传递参数的时间和空间效率都好。
- 指针参数虽然也能达到与使用引用的效果,但在被调函数中需要重复使用“*指针变量名”的形式进行运算,这很容易产生错误且程序的阅读性交差;另一方面,在主函数的调用点处,必须用变量的地址作为实参。
#include<iostream.h> void main(){int i=5;int &j=i;//j是一个引用类型,代表i的一个替代名i值改变时,j值也跟着改变,所以会输出i=7,j=7i=7;cout<<"i="<<i<<"j="<<j; }#include<iostream.h> void swap(float &m,float &n){float temp;temp=m;m=n;n=temp; } void main(){float a,b;cin>>a>>b;swap(a,b);cout<<a<<endl<<b<<endl; } -
-
-
形参
&L和L的区别:带&的是引用型参数,它是地址传递,其实参会随着形参的改变而改变;不带&的参数是一般参数,是值传递,其实参不会随着形参的改变而改变。所以,结构改变,并且需要传回这种改变的要用引用型参数,否则用一般参数。
- 引用
L->length等同于(*L)length
2.1建立
这里介绍整体创建顺序表,即由数组元素a[0…n-1]创建顺序表L。其方法是将数组a中的每个元素依次放入顺序表中,并将n赋给顺序表的长度域。算法如下:
void CreatList(SqList *&L,ElemType a[],int n){//由a中的n个元素建立顺序表int i=0,k=0;//k表示L中元素的个数,初始值为0L=(SqList*)malloc(sizeof(SqList));//分配存放线性表的空间while(i<n){//i扫描数组a的元素L->data[k]=a[i];//将元素a[i]存放到L中k++;i++;}L->length=k;//设置L的长度K
}
调用上述算法创建好L所指的顺序表之后,需要回传给对应的实参,也就是说L是输出型参数,所以在形参L的前面需要加上引用符"&".
2.2初始化(InitList(&L))
该运算功能是构造一个空的线性表L,实际上只需分配线性表的存储空间并将length域设置为0即可。算法如下:
void InitList(SqList *&L){L=(SqList*)malloc(sizeof(SqList));//分配存放线性表的空间L->length=0;;//置空线性表的长度为0
}
本算法的时间复杂度为O(1)。
2.3销毁(DestroyList(&L))
该运算功能是释放线性表L占用的内存空间。算法如下:
void DestroyList(SqList *&L){free(L);//释放L所指的顺序表空间
}
本节的顺序表是通过malloc函数分配存储空间的,当不再需要顺序表时务必调用DestroyList基本运算释放其存储空间;否则,尽管系统会自动释放顺序表的指针变量L,但不会自动释放L指向的存储空间,如此可能会造成内存泄漏,本算法的时间复杂度为O(1).
2.4判断线性表是否为空表(ListEmpty(L))
该运算返回一个布尔值表示L是否为空表。若L为空表,返回true,否则返回false。算法如下:
bool ListEmpty(SqList *L){return(L->length==0);
}
2.5求线性表的长度(ListLength(L))
该运算返回顺序表L的长度,实际上只需返回length域的值即可。算法如下:
bool ListEmpty(SqList *L){return(L->length==0)
}
2.6输出线性表(DispList(L))
该运算依次输入L中各元素的值。算法如下:
void DispList(SqList *L){for(int i=0;i<L->length;i++)printf("%d",L->data[i]);printf("\n");
}
本算法中的基本操作为for循环中的printf语句,故时间复杂度为O(n)
2.7查找元素的操作(GetElem与LocateElem)
2.7.1按序号(GetElem(L,i,&e))
实现GetElem的具体操作,即将线性表L中的第i个位置元素值返回。就程序而言,我们只需要把数组第i-1下标的值返回即可。
bool GetElem(SqList *L,ElemType e){int i=0;while(i<1||i>L->length)return false;//参数i错误时返回falsee=L->data[i-1];//取元素的值return true;//成功找到元素时返回true
}
本算法的时间复杂度为O(1)
2.7.2按元素(LocateElem(L,e))
按运算顺序查找第一个值为e的元素的逻辑符号,若这样的元素不存在,则返回为0.算法如下:
int LocateElem(SqList *L,ElemType e){int i=0;while(i<L->length && L->data[i]!=e)i++;//查找元素eif(i>=L->length)return 0;//未找到时返回0elsereturn i+1;//找到后返回其逻辑符号
}
该算法的时间复杂度为O(n)
2.8插入数据元素(ListInsert(&L,i,e))
刚才我们提到过排队的问题,如果这时候有一个人要回到队列当中,我们应该怎么做,我们会找到他要插入位置的那个同学,让他以及它后面的同学全部往后移动一个位置,再将新同学安排在这个位置里面。所以我们插入算法的思路如下:
- 如果插入位置不合理,抛出异常;
- 如果线性表长度大于等于数组长度,则抛出异常或动态增加数组容量;
- 从最后一个元素开始向前遍历到第i个位置,分别将他们都向后移动一个位置;
- 将要插入元素填入位置i处;
- 线性表长度+1;
算法如下:
Status ListInsert(SqList *L,int i,ElemType e){int k;if(L->length==MAXSIZE){//顺序线性表已经满了return ERROR;}if(i<1||i>L->length+1){//当i不在范围内时return ERROR;}if(i<=L->length){//若插入数据位置不在表尾//将要插入位置后数据元素向后移动一位for(k=L->length-1;k>=i;k--){L->data[k+1]=L->data[k];}}L->data[i-1]=e;//将新元素插入L->length++;return true;
}
时间复杂度为O(n)
2.9删除数据元素(ListDelet(&L,i,&e))
我们完全可以借鉴前面插入数据元素的算法,得到删除数据算法的思路:
-
如果删除位置不合理,抛出异常;
-
取出删除元素
-
从删除元素位置开始遍历到最后一个元素位置,分别将它们都向前移动一个位置;
-
表长-1
算法如下:
Status ListDelet(SqList *L,int i,ElemType *e){int k;if(L->length==0){return ERROR;}if(i<1||i>L->length){return ERROR;}*e=L->data[i-1];if(i<L->length){for(k=i;k<L->length;k++){L->data[k-1]=L->data[k];}}L->length--;return true;
}
三.顺序表优缺点
线性表的顺序存储结构,在存、读数据时,不管是哪个位置,时间复杂度都是O(1)。而在插入或删除数据时,时间复杂度都是O(n)。这就说明,它比较适合元素个数比较稳定,不经常插入和删除元素,而更多的操作是存取数据的应用。那么我们可以得出它的优缺点:
优点:
- 无需为表示表中元素之间的逻辑关系而增加额外的存储空间。
- 可以快速地存取表中任意位置的元素。
缺点:
- 插入和删除操作需要移动大量元素。
- 当线性表长度变化较大时,难以确定存储空间的容量。
- 容易造成存储空间的“碎片”(因为申请空间的时候是一整块一整块地申请的,那么两块地的中间就会有一小块碎片的地方被浪费)
相关文章:

【数据结构与算法】线性表顺序存储结构
文章目录 一.顺序表的存储结构定义1.1定义1.2 图示1.3结构代码*C语言的内存动态分配 二.顺序表基本运算*参数传递2.1建立2.2初始化(InitList(&L))2.3销毁(DestroyList(&L))2.4判断线性表是否为空表(ListEmpty(L))2.5求线性表的长度(ListLength(L))2.6输出线性表(DispLi…...
Unix Standardization and Implementations
Unix标准化 在Unix未制定较为完备的标准时,各个平台的系统调用方式各异,所开发出的应用程序存在可移植性差的特点,因此人们呼吁指定一套Unix标准来规范接口,增加应用程序的可移植性。所谓Unix标准即适用于Unix环境下的一系列函数…...

Windows 与 Java 环境下的 Redis 利用分析
1 前言 在最近的一次攻防演练中,遇到了两个未授权访问的 Redis 实例。起初以为可以直接利用,但后来发现竟然是Windows Java (Tomcat)。因为网上没有看到相关的利用文章,所以在经过摸索,成功解决之后决定简单写一写。 本文介绍了…...
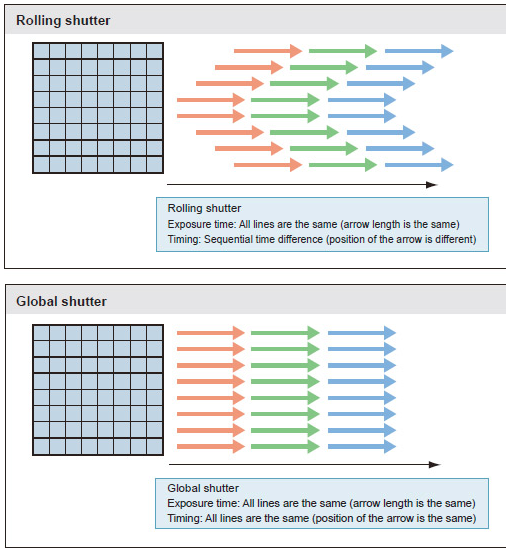
机器视觉系统硬件组成之工业相机篇
工业相机是一种非常重要的机器视觉器件,它能够将被采集的图像信息通过电路转换成电信号,再通过模数转换器(ADC)将其转化为数字信号,最后以标准的视频信号输出。工业相机在机器视觉领域得到了广泛应用,包括质…...
离线安装bitnami-gitlab8.8.4+汉化
注意: 常规安装gitlab需要联网,而按装bitnami-gitlab无需联网(bitnami-gitlab用于内网环境无法联网时安装gitlab,两者是一个东西只是名字不一样)bitnami-gitlab-8.8.4版本可以汉化成功新用户注册账户无需激活也可以直接登录,因为…...
亚马逊日本站推出AI日语listing功能,Listing一键发布,轻松无忧!
随着大数据与人工智能技术的成熟,AI在电商的应用也越来越多,各大电商平台都在陆续引进AI人工智能,有客服方面的,也有发布Listing方面的。 10月17日消息,亚马逊日本站近日宣布推出一项支持日语的人工智能listing功能&am…...

Golang | Leetcode Golang题解之第475题供暖器
题目: 题解: func findRadius(houses, heaters []int) (ans int) {sort.Ints(houses)sort.Ints(heaters)j : 0for _, house : range houses {dis : abs(house - heaters[j])for j1 < len(heaters) && abs(house-heaters[j]) > abs(house-…...
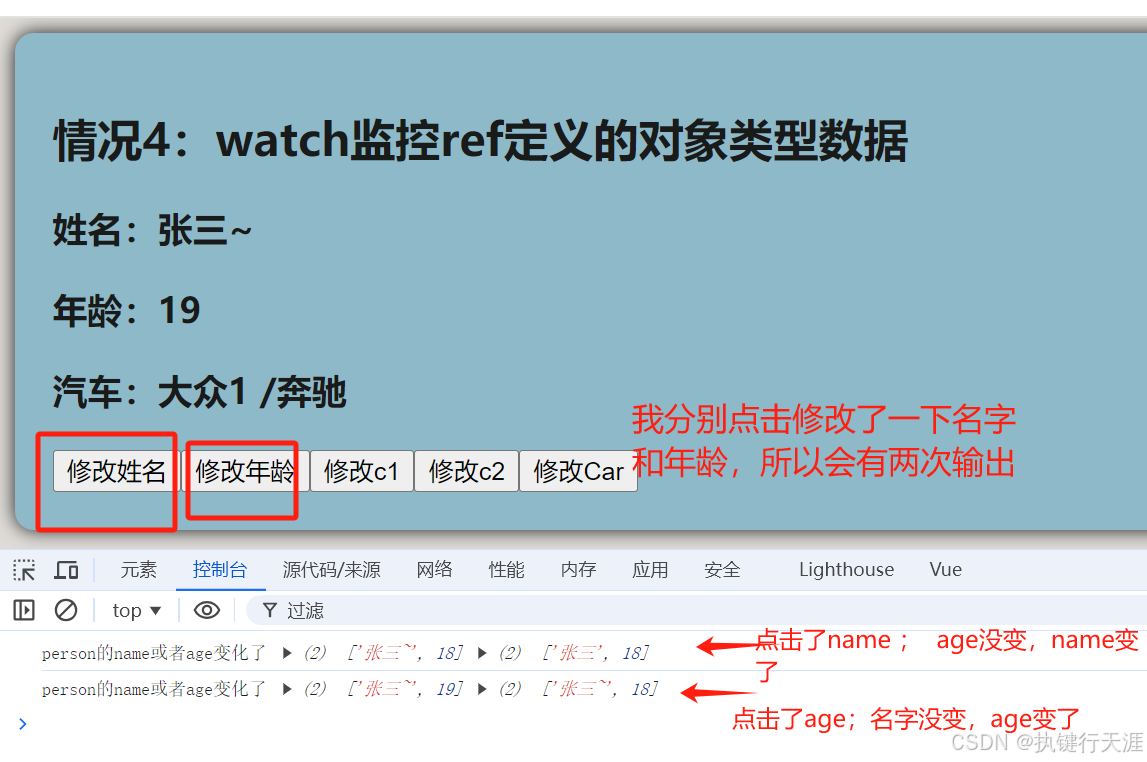
【Vue】Vue3.0 (十二)、watchEffect 和watch的区别及使用
上篇文章: 【Vue】Vue3.0 (十二)、watch对ref定义的基本类型、对象类型;reactive定义的对象类型的监视使用 🏡作者主页:点击! 🤖Vue专栏:点击! ⏰️创作时间&…...

PHP-laravel框架
laravel框架 laravel 搭建与路由基础 基本路由与视图路由 视图使用控制器模板分配变量...
永恒之蓝漏洞
MS17-010是微软于2017年3月发布的一个安全补丁,旨在修复Windows操作系统中的一个严重漏洞,该漏洞被称为“永恒之蓝”(EternalBlue)。这个漏洞影响了Windows的Server Message Block(SMB)协议,允许…...
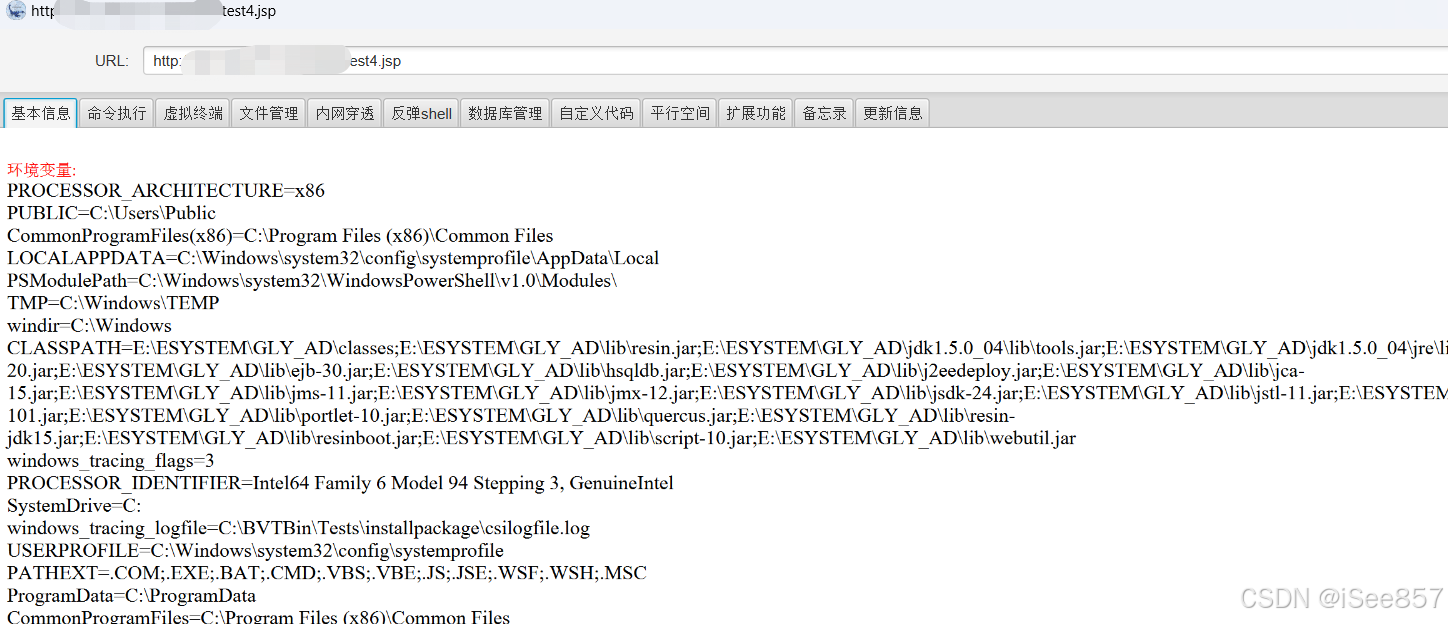
Eking管理易 Html5Upload 前台任意文件上传漏洞复现
0x01 产品描述: Eking管理易是一款专为广告制品制作企业量身定制的管理软件产品,旨在帮助企业实现规范化、科学化管理,提升运营效率和降低运营成本。 该软件由广州易凯软件技术有限公司开发,基于JAVA企业版技术研发࿰…...
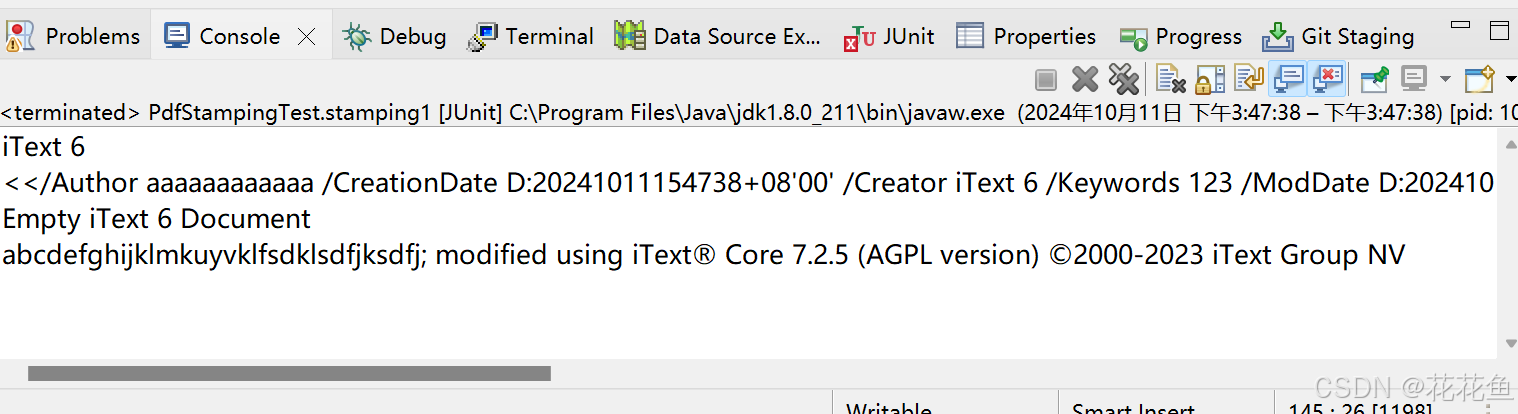
spring boot itext7 修改生成文档的作者、制作者、标题,并且读取相关的信息。
1、官方的example文件:iText GitHub itext-java-7.2.5\kernel\src\test\java\com\itextpdf\kernel\pdf\PdfStampingTest.java 2、修改代码: Testpublic void stamping1() throws IOException {String filename1 destinationFolder "stamping1_…...
LeetCode题练习与总结:灯泡开关--319
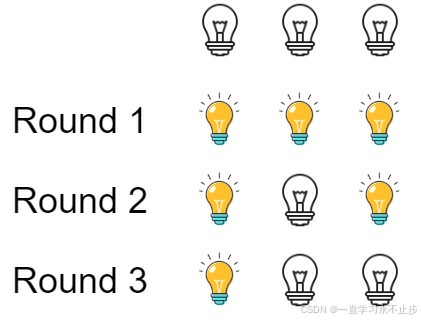
一、题目描述 初始时有 n 个灯泡处于关闭状态。第一轮,你将会打开所有灯泡。接下来的第二轮,你将会每两个灯泡关闭第二个。 第三轮,你每三个灯泡就切换第三个灯泡的开关(即,打开变关闭,关闭变打开&#x…...
ClickFix攻击活动升级:可通过虚假谷歌会议画面传播恶意软件
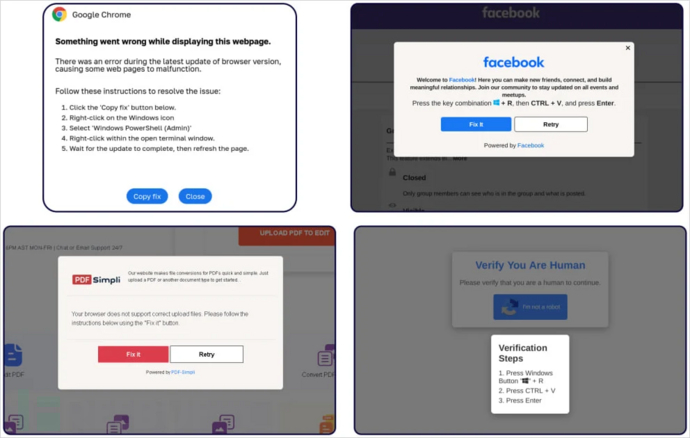
最近,研究人员报告了一种新的 ClickFix 攻击活动,主要通过诱骗用户访问显示虚假连接错误的欺诈性 谷歌会议的页面,继而借此传播信息窃取恶意软件,主要针对 Windows 和 macOS 操作系统。 ClickFix是网络安全公司Proofpoint在5月份…...

迷茫!能走出迷茫?
我今年40有余,因资质平庸,及特殊的个人经历,仍奋斗在一线。上班近二十年,两件事对我人生走向影响最大,编程和炒股。 下个月要去一家新公司上班。今天算是在现公司工作交接的最后时段。在这家公司干了接近一年ÿ…...

6.2 遍历重定位表
本节我们将编写一个遍历重定位表的示例程序,打印重定位表。 本节必须掌握的知识点: 遍历重定位表 6.2.1 遍历重定位表 实验四十三:遍历重定位表 以下代码实现打印"c:\\notepad64.exe"进程重定位表的所有信息。 /*--------------…...

面对服务器掉包的时刻困扰,如何更好的解决
在数字化时代,服务器的稳定运行是企业业务连续性的基石。然而,服务器“掉包”现象,即数据包在传输过程中丢失或未能正确到达目的地的情况,却时常成为IT运维人员头疼的问题。它不仅影响用户体验,还可能导致数据不一致、…...
RTSP流图片采样助手(yolov5)
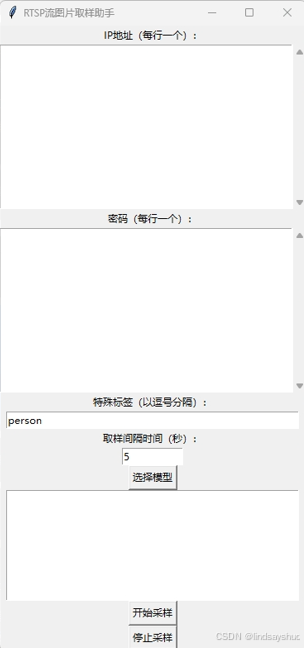
在监控和视频分析领域,实时采样视频流中的图像数据是十分重要的。本文将介绍一个基于Python和Tkinter构建的RTSP流图片采样助手的设计与实现,旨在简化RTSP流的采样过程,并支持根据用户定义的特殊标签进行筛选。 项目概述 该项目的主要功能包…...

MySQL、MariaDB、OceanBase远程异地定时备份脚本
问题背景 公司需要在异地机房远程备份数据库,以防止数据丢失,同时要支持MySQL、MariaDB和OceanBase。由于MariaDB和OceanBase支持MySQL语法,所以可以直接用MySQL Client进行备份。 安装MySQL客户端 yum install mysql编写脚本 编写/backu…...
【远程监控新体验】OpenObserve结合内网穿透无公网IP远程访问全攻略
文章目录 前言1. 安装Docker2. Docker镜像源添加方法3. 创建并启动OpenObserve容器4. 本地访问测试5. 公网访问本地部署的OpenObserve5.1 内网穿透工具安装5.2 创建公网地址6. 配置固定公网地址前言 本文主要介绍如何在Linux系统使用Docker快速本地化部署OpenObserve云原生可观…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...
