《Vue3 踩坑》expose 和 defineExpose 暴露属性或方法注意事项
选项式写法
使用 选项式API - 状态选项 - expose 一定要注意:

接下来,进一步看示例说明:
设置 expose
- 仅显示列出的属性/方法才能被父组件调用;
- 代码第 2 行,父组件可访问属性
a和 方法myFunc01,不可访问属性b和 方法myFunc02;
export default {expose: ['a', 'myFunc01'],data() {return {a: 1,b: 2}},methods: {myFunc01(){//...},myFunc02(){//...}}
}
</script>
不设置expose
- 默认全部属性/方法都可被父组件调用;
- 父组件可访问
a、b、myFunc01,myFunc02等全部属性/方法!我就在这里犯错了…
export default {data() {return {a: 1,b: 2}},methods: {myFunc01(){//...},myFunc02(){//...}}
}
组合式写法
设置 defineExpose
- 组合式写法默认所有属性和方法都是私有的,需要使用 defineExpose 宏显示暴露;
- 代码 15-18 行,父组件只能调用属性
a和方法myFunc01; defineExpose无需引入,在<script setup>中可直接使用;
<script setup>
import { ref } from 'vue'const a = ref(1)
const b = ref(2)function myFunc01(){//...
}function myFunc02(){//...
}defineExpose({a,myFunc01
})
</script>
相关文章:

《Vue3 踩坑》expose 和 defineExpose 暴露属性或方法注意事项
选项式写法 使用 选项式API - 状态选项 - expose 一定要注意: 接下来,进一步看示例说明: 设置 expose 仅显示列出的属性/方法才能被父组件调用;代码第 2 行,父组件可访问属性 a 和 方法 myFunc01,不可访…...

10.13论文阅读
通过联合学习检测和描述关键点增强可变形局部特征 摘要 局部特征提取是计算机视觉中处理图像匹配和检索等关键任务的常用方法。大多数方法的核心理念是图像经历仿射变换,忽略了诸如非刚性形变等更复杂的效果。此外,针对非刚性对应的新兴工作仍然依赖于…...

六西格玛黑带项目:TBX-02无人机飞行稳定性提升——张驰咨询
一、项目背景与问题定义 TBX-02是该公司最新发布的消费级无人机,面向摄影爱好者和户外探险者。产品上市后,通过客户反馈和实际测试数据发现,该无人机在复杂飞行环境中,如强风或快速移动时,存在明显的飞行抖动和稳定性…...

git clone 国内镜像
比如 git clone https://github.com/HKUST-Aerial-Robotics/A-LOAM.git 改成 git clone https://gitclone.com/github.com/HKUST-Aerial-Robotics/A-LOAM.git...

【服务器虚拟化】
服务器虚拟化是一种将一台物理服务器划分为多个虚拟服务器的技术,每个虚拟服务器都可以独立运行操作系统和应用程序。下面是一个详细的教程,以KVM虚拟化为例,介绍了具体的操作步骤和执行命令。 准备工作 a. 确保你的服务器支持虚拟化技术&…...
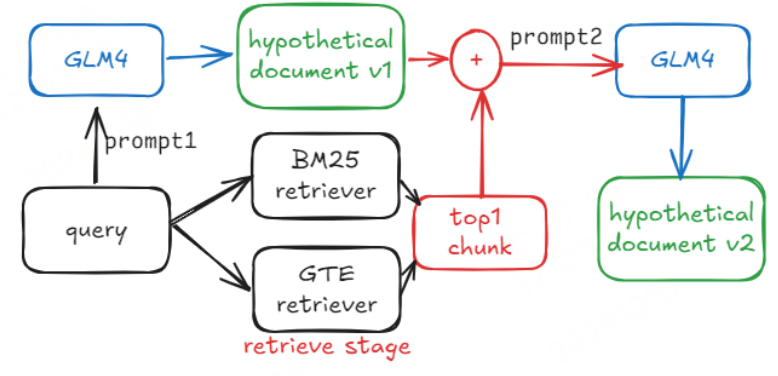
【RAG】aiops第一名方案-EasyRAG:自动网络运营的高效检索增强生成框架
来看一个RAG比赛方案,提出了一个名为EasyRAG的框架,用于自动化网络操作的检索增强生成。该框架旨在解决网络操作中信息检索和生成效率低、准确性差的问题。研究难点包括:如何在保证准确性的前提下提高检索和生成的效率;如何实现简…...
3款备受好评的电脑数据恢复软件,赶紧收藏以备不时之需
在日常工作和生活中,电脑数据丢失是许多人都会遇到的问题。无论是误删文件、硬盘格式化,还是系统崩溃,都可能导致重要数据的丢失。所以,好用的数据恢复软件必不可少。 但在如今的市场上数据恢复软件琳琅满目,它们在恢复…...

.net core 实现多线程方式有哪些
在 .NET Core 中,有多种方式可以实现多线程编程。这些方式包括使用 Thread 类、Task 和 Parallel 类库。每种方法都有其适用场景和优缺点。下面我将通过代码示例来展示这些不同的多线程实现方式。 1. 使用 Thread 类 Thread 类是 .NET 中最基本的多线程实现方式。…...

《Linux从小白到高手》综合应用篇:深入理解Linux磁盘及IO优化
1. 前言 其实磁盘优化和IO优化,我在前面的其他Linux调优博文中已经讲述过或者涉及过了,但是太过零碎,所以本篇就来集中深入讨论下Linux磁盘和IO调优。 2.磁盘调优 结合我多年的经验,本人认为磁盘调优最重要的是读写性能的提升和…...

【Linux】内存文件系统的I/O、重定向
文章目录 1. 系统中的文件2. 回顾C中的文件接口3. 文件类的系统调用3.1 open3.2 文件描述符 4. IO的基本过程5.重定向5.1 引入重定向5.2 系统中的重定向接口 6. 缓冲区问题7. 简单版shell的实现 1. 系统中的文件 在学习完Linux权限后,我们清楚的知道:文…...

力扣10.18
1463. 摘樱桃 II 给你一个 rows x cols 的矩阵 grid 来表示一块樱桃地。 grid 中每个格子的数字表示你能获得的樱桃数目。 你有两个机器人帮你收集樱桃,机器人 1 从左上角格子 (0,0) 出发,机器人 2 从右上角格子 (0, cols-1) 出发。 请你按照如下规则…...

cs木马图形化界面出现问题处理
一个月多月没用cs木马了,发现打开客户端之后显示不出图形化界面,且出现下面这样的报错。 、 最后发现是java版本的问题,kali的java自动更新了。把原来的openjdk11改到了openjdk23。 解决方法: 输入: sudo update-…...

数据结构与算法 - 树 #数的概念 #二叉树 #堆 - 堆的实现/堆排序/TOP-K问题
文章目录 前言 一、树 (一)、概念 1、树的定义 (二)、树的定义 1、树为什么是递归定义的? 2、如何定义树(如何表达一棵树) 解决方案一:假设我们得知该树的度 解决方案二:顺序表 解决方案三:左孩子右兄弟表示法 二、二叉…...

Git推送被拒
今天开发完成一个新的需求,将自己的分支合并到test分支后,推送到远程仓库,结果显示推送被拒: 原因是因为有人更新了test分支的代码,我在合并之前没有拉取最新的test分支代码,所以他提示我“推送前需要合并…...
Jmeter进行http接口测试
🍅 点击文末小卡片 ,免费获取软件测试全套资料,资料在手,涨薪更快 本文主要针对http接口进行测试,使用jmeter工具实现。 Jmeter工具设计之初是用于做性能测试的,它在实现对各种接口的调用方面已经做的比较…...

工业相机详解及选型
工业相机相对于传统的民用相机而言,具有搞图像稳定性,传输能力和高抗干扰能力等,目前市面上的工业相机大多数是基于CCD(Charge Coupled Device)或CMOS(Complementary Metal Oxide Semiconductor)芯片的相机。 一,工业相机的分类 …...

RAID 矩阵
在架构设计中,RAID矩阵(RAID Log)是一个用于项目管理和风险管理的工具,帮助团队有效管理和跟踪项目中可能影响成功交付的关键因素。与存储技术中的 RAID 不同,这里的 RAID 是一个缩写,代表: R:…...

详细分析Redisson分布式锁中的renewExpiration()方法
目录 一、Redisson分布式锁的续期 整体分析 具体步骤和逻辑分析 为什么需要递归调用? 定时任务的生命周期? 一、Redisson分布式锁的续期 Redisson是一个基于Redis的Java分布式锁实现。它允许多个进程或线程之间安全地共享资源。为了实现这一点&…...

实验3,网络地址转换
实验3:网络地址转换 实验目的及要求: 通过实验,掌握NAT技术的工作原理,了解三种不同类型NAT技术的主要作用以及各自的主要应用环境。能够完成静态NAT和复用NAT技术的应用,并熟练掌握NAT技术相关的配置命令。 实验设…...

Java 中的 String 字符串是不可变的
文章目录 什么是不可变字符串?举个例子直观理解 不可变的原理1. 内部实现2. 字符串常量池3. 线程安全 为什么要设计成不可变?什么时候用可变字符串?示例 总结推荐阅读文章 在 Java 编程中,字符串(String)是…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...
