牛客小白月赛102:最短?路径(分层bfs)
链接:登录—专业IT笔试面试备考平台_牛客网
来源:牛客网
题目描述
给定一个 nnn 个点 mmm 条边的无向图,LH 打算从点 111 出发去点 nnn。
假如 LH 到达了一个点 iii,那么他可以选择在这个点花费 aia_iai 的时间休息后继续赶路,或者不休息然后花费 111 的时间简单整顿后继续赶路。
LH 不能连续超过 kkk 个节点不休息,问从 111 到 nnn 的最短时间。
注意:假如 LH 到达了点 nnn 也需要选择休息或者不休息。
输入描述:
第一行输入一个整数 T(1≤T≤104)T(1\le T\le 10^4)T(1≤T≤104),表示测试用例组数。接下来是 TTT 个测试用例。每个测试用例第一行包含三个整数 n,m,k(2≤n≤2×105,1≤m≤3×105,0≤k≤10)n,m,k(2\le n\le 2\times 10^5,1\le m\le 3\times 10^5,0\le k\le 10)n,m,k(2≤n≤2×105,1≤m≤3×105,0≤k≤10)。 第二行输入 nnn 个整数 ai(0≤ai≤109)a_i(0\le a_i\le 10^9)ai(0≤ai≤109),表示在第 iii 个点休息需要花费的时间。随后 mmm 行每行两个整数 u,vu ,vu,v,表示 uuu 和 vvv 之间有一条无向边。
保证输入的图联通,没有重边和自环。
保证所有测试用例 nnn 的和不超过 2×1052\times 10^52×105,mmm 的和不超过 3×1053\times 10^53×105。
输出描述:
对于每个测试用例,输出一个整数,表示 LH 从 111 到 nnn 的最短时间。
示例1
输入
复制1 5 6 2 7 7 3 6 4 4 5 1 3 3 4 5 2 2 4 1 4
1 5 6 2 7 7 3 6 4 4 5 1 3 3 4 5 2 2 4 1 4
输出
复制6
6
说明
一种可能的最优方案为 1−>4−>51->4->51−>4−>5。其中点 111 和点 444 不休息,在点 555 休息,总时间为 1+1+a5=61+1+a_5=61+1+a5=6。
示例2
输入
复制2 20 30 8 9 10 2 8 1 6 7 10 6 10 7 0 0 3 4 0 7 9 4 3 18 4 8 10 17 6 11 3 7 4 7 14 3 8 10 19 16 8 11 4 13 14 17 14 4 15 12 5 12 17 16 9 5 20 7 2 1 4 10 5 14 15 3 5 17 8 16 6 9 10 16 17 4 2 17 20 10 7 16 1 20 30 3 2 0 2 2 9 6 7 2 5 3 7 1 8 8 8 3 1 0 8 9 1 17 11 8 17 16 14 19 7 6 3 4 10 15 4 9 14 18 20 5 7 8 18 10 3 6 7 1 5 14 13 5 14 3 15 2 12 13 7 3 6 18 2 10 9 3 1 14 11 4 3 17 14 10 7 14 13 8 6 5
2 20 30 8 9 10 2 8 1 6 7 10 6 10 7 0 0 3 4 0 7 9 4 3 18 4 8 10 17 6 11 3 7 4 7 14 3 8 10 19 16 8 11 4 13 14 17 14 4 15 12 5 12 17 16 9 5 20 7 2 1 4 10 5 14 15 3 5 17 8 16 6 9 10 16 17 4 2 17 20 10 7 16 1 20 30 3 2 0 2 2 9 6 7 2 5 3 7 1 8 8 8 3 1 0 8 9 1 17 11 8 17 16 14 19 7 6 3 4 10 15 4 9 14 18 20 5 7 8 18 10 3 6 7 1 5 14 13 5 14 3 15 2 12 13 7 3 6 18 2 10 9 3 1 14 11 4 3 17 14 10 7 14 13 8 6 5
输出
复制3 5
3 5
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e5+10;
int n,m,k,a[N];
int vis[N][20],dis[N][20];
struct ty{int dis,x,k;bool operator < (const ty &a) const{return dis>a.dis;}
};
void solved(){cin>>n>>m>>k;for(int i=1;i<=n;i++) cin>>a[i];for(int i=1;i<=n;i++){for(int j=0;j<=k;j++){vis[i][j]=0;dis[i][j]=0x3f3f3f3f3f3f3f3f;}}vector<int> g[n+1];for(int i=1;i<=m;i++){int u,v;cin>>u>>v;g[u].push_back(v);g[v].push_back(u);}priority_queue<ty> q;q.push({a[1],1,0});//休息dis[1][0]=a[1];if(k!=0){q.push({1,1,1});dis[1][1]=1;}while(q.size()){ty tmp=q.top();q.pop();if(vis[tmp.x][tmp.k]) continue;vis[tmp.x][tmp.k]=1;for(auto x:g[tmp.x]){if(tmp.k==k){if(dis[x][0]>dis[tmp.x][tmp.k]+a[x]){//休息dis[x][0]=dis[tmp.x][tmp.k]+a[x];q.push({dis[x][0],x,0});}continue;}if(dis[x][0]>dis[tmp.x][tmp.k]+a[x]){//休息dis[x][0]=dis[tmp.x][tmp.k]+a[x];q.push({dis[x][0],x,0});}if(dis[x][tmp.k+1]>dis[tmp.x][tmp.k]+1){dis[x][tmp.k+1]=dis[tmp.x][tmp.k]+1;q.push({dis[x][tmp.k+1],x,tmp.k+1});}}}int ans=0x3f3f3f3f3f3f3f3f;for(int i=0;i<=k;i++){ans=min(ans,dis[n][i]);}cout<<ans<<endl;}
signed main(){cin.tie(0);ios::sync_with_stdio(0);int t;cin>>t;while(t--){solved();}
}相关文章:
)
牛客小白月赛102:最短?路径(分层bfs)
链接:登录—专业IT笔试面试备考平台_牛客网 来源:牛客网 题目描述 给定一个 nnn 个点 mmm 条边的无向图,LH 打算从点 111 出发去点 nnn。 假如 LH 到达了一个点 iii,那么他可以选择在这个点花费 aia_iai 的时间休息后继续赶…...

JSON字符串转成java的Map对象
要将这个JSON字符串转换成Java对象,你可以定义一个Element类来表示每个要素,然后使用一个Map来存储这些要素。以下是具体的实现步骤: 步骤 1: 定义 Element 类 首先,定义一个Element类来表示每个要素的结构: public…...
-为什么巴比伦塔会失败?(Why Did the Tower of Babel Fail?))
重读《人月神话》(8)-为什么巴比伦塔会失败?(Why Did the Tower of Babel Fail?)
据《创世纪》记载,巴比伦塔是人类继诺亚方舟之后的第二大工程壮举,但巴比伦塔同时也是第一个彻底失败的工程。 巴比伦塔的管理教训 这个项目具备了几乎所有成功的先决条件: 有清晰的目标,尽管目标理想化到了近乎不可实现的地步&…...
STL源码剖析:Hashtable
hashtable 概述 哈希表是一种数据结构,它提供了快速的数据插入、删除和查找功能。它通过使用哈希函数将键(key)映射到表中的一个位置来实现这一点,这个位置称为哈希值或索引。哈希表使得这些操作的平均时间复杂度为常数时间&…...

spring-boot学习(2)
上次学习截止到拦截器 1.构建RESfun服务 PathVariable通过url路径获取url传递过来的信息 2.MyBatisPlus 第三行的mydb要改为自己的数据库名 第四,五行的账号密码改成自己的 MaooerScan告诉项目自己的这个MyBatisPlus是使用在哪里的,包名 实体类的定义…...

《案例》—— OpenCV 实现2B铅笔填涂的答题卡答案识别
文章目录 一、案例介绍二、代码解析 一、案例介绍 下面是一张使用2B铅笔填涂选项后的答题卡 使用OpenCV 中的各种方法进行真确答案识别,最终将正确填涂的答案用绿色圈出,错误的答案不圈出,用红色圈出错误题目的正确答案最终统计正确的题目数…...
新员工入职流程指南_完整入职流程解析
文章介绍了新员工入职流程的重要性、步骤及持续时间,并推荐ZohoPeople软件自动化管理入职流程,提升新员工入职体验,减少离职率,确保合规性,提升公司品牌形象。 一、新员工入职流程是怎样的? 入职流程是指一…...

mysql查看和修改默认配置
1.查看最大连接数 SELECT max_connections; 或者 SHOW VARIABLES LIKE max_connections;2.查看当前连接的客户端 SHOW PROCESSLIST;2.临时设置最大连接数 SET GLOBAL max_connections 500;3.临时设置连接客户端交互超时时间 SET GLOBAL interactive_timeout 1800;4.永久生…...

海外云手机:出海电商养号智能化方案
随着出海电商的迅猛发展,使用海外云手机进行养号已经成为越来越多商家的新选择。尤其在社交电商推广和短视频引流方面,海外云手机不仅提高了流量的精准度,还助力商家实现业务的快速增长。本文将探讨海外云手机养号相较于传统模式的优势&#…...
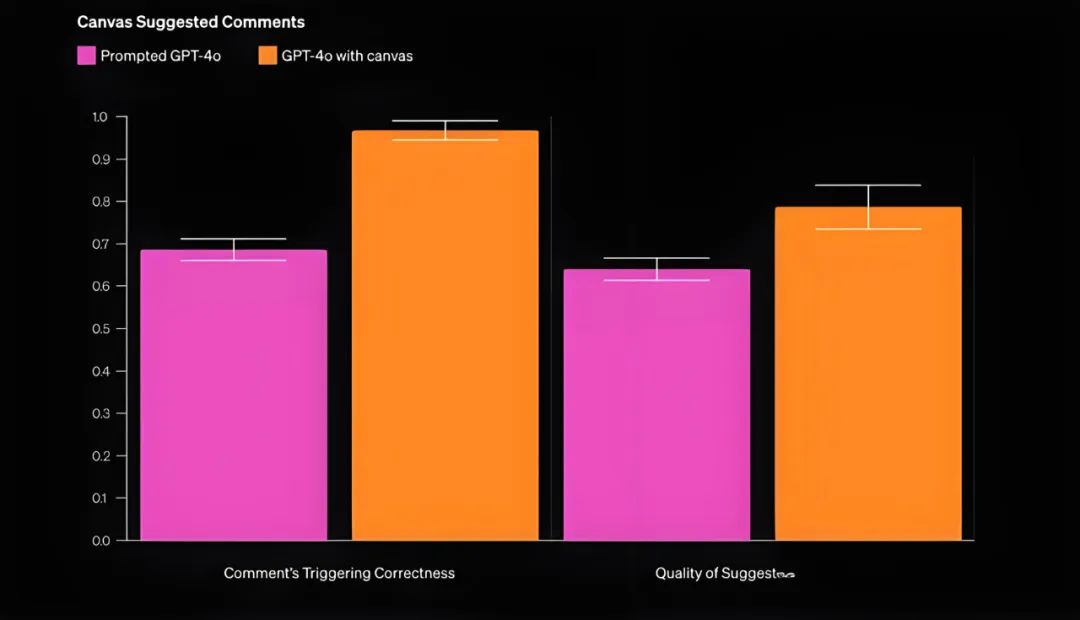
OpenAI Canvas用户反馈:并不如外界传言般“炸裂”,更不是“AGI的终极交互形态” | LeetTalk Daily...
“LeetTalk Daily”,每日科技前沿,由LeetTools AI精心筛选,为您带来最新鲜、最具洞察力的科技新闻。 Canvas作为一个独立的界面,通过与ChatGPT的结合来提升用户的协作能力和创作效率。尽管用户对其独立性与现有工具的整合存在不同…...

RiproV9.0主题wordpress主题免扩展可二开PJ版/WordPress博客主题Ripro全解密无后门版本
🔥🎉 全新RiPro9.0开源版发布 —— 探索无限可能🚀🌐 今天,我很高兴能与大家分享一个重磅资源——RiPro9.0开源版!这不是一个普通的版本,而是一个经过精心打磨、全面解密的力作。🔍…...

[LeetCode] 515. 在每个树行中找最大值
题目描述: 给定一棵二叉树的根节点 root ,请找出该二叉树中每一层的最大值。 示例1: 输入: root [1,3,2,5,3,null,9] 输出: [1,3,9]示例2: 输入: root [1,2,3] 输出: [1,3]提示: 二叉树的节点个数的范围是 [0,10…...

【分布式微服务云原生】《微服务架构大揭秘:流行框架与服务治理攻略》
标题:《微服务架构大揭秘:流行框架与服务治理攻略》 摘要:本文深入探讨了流行的微服务架构框架,包括 Spring Cloud、Docker Kubernetes、Dubbo、Service Mesh 和 Serverless 架构,详细介绍了它们的关键组件和服务治理…...

uniapp uni.uploadFile errMsg: “uploadFile:fail
uniapp 上传后一直显示加载中 1.检查前后端上传有无问题 2.检查失败信息 await uni.uploadFile({url,filePath,name,formData,header,timeout: 30000000, // 自定义上传超时时间fail: async function(err) {$util.hideAll()// 失败// err 返回 {errMsg: "uploadFile:fai…...

一个常见问题:TCP和UDP是否可以使用一个端口
TCP(传输控制协议)和UDP(用户数据报协议)做为两种被广泛使用的协议,它们在处理数据时采用不同的机制,那么有一个问题,在同一系统内,TCP和UDP的服务是否可以使用同一个端口呢…...
)
前端报错:‘vue-cli-service‘ 不是内部或外部命令,也不是可运行的程序(node_modules下载不下来)
原因:Vue CLI 没有被正确安装,或者其安装路径没有被添加到你的系统环境变量中。 一、确认 Vue CLI 是否已安装: 打开命令行工具(例如 CMD、PowerShell、Terminal),输入以下命令来检查 Vue CLI 是否已安装…...

白日门【鬼服无限刀】win服务端+安卓客户端+教程+GM后台
演示系统:Windows Server 2012 -------------------------------------------------------------------------------------------------------------------------- 把服务端上传解压缩到服务器D盘根目录:D:\【解压完成后检查路径是否正确:D:\】 安装基础运行环境&…...

如何迅速的了解一个人
目录 社会经济背景 生活满意度 爱心和同情心 如果你想迅速地了解一个人,问他问题是最快捷的方法。不论你是相亲、工作、而试、看医生还是为孩子找个学校,事先设计好你想提出的问题,想好你究竟要搜罗对方哪一方面的信息这样做会实现许多目…...

Window和Linux远程调度kettle
在windows和linux分别安装kettle,我的是pdi-ce-8.2.0.0-342版本,在windows中配置好之后,直接放到虚拟机的目录下 在cmd窗口中到kettle根目录下执行 (carte ip 端口 ),出现如下提示即启动成功 在远程端…...

设定义结构变量
在C语言中,可以使用struct关键字来定义结构变量。结构变量是由多个不同类型的成员变量组成的数据类型,可以在一个变量中存储多个相关的数据。 定义结构变量的语法如下: struct 结构名 {数据类型 成员1;数据类型 成员2;... };例如࿰…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...
