复合泊松过程
复合泊松过程的均值、方差与特征函数

复合泊松过程的定义
复合泊松过程 ( Y(t) ) 是一种常见的随机过程,通常定义为:
Y ( t ) = ∑ k = 1 N ( t ) X k Y(t) = \sum_{k=1}^{N(t)} X_k Y(t)=k=1∑N(t)Xk
其中:
- ( N(t) ) 是一个强度为 ( \lambda ) 的泊松过程,表示在时间 ( t ) 内发生的事件个数;
- ( X_k ) 是一组独立同分布的随机变量,表示每次事件的独立增量。
均值推导
为了推导复合泊松过程的均值 ( \mathbb{E}[Y(t)] ),我们首先利用泊松过程和条件期望的性质。
泊松过程的均值:
泊松过程 ( N(t) ) 的均值为:
E [ N ( t ) ] = λ t \mathbb{E}[N(t)] = \lambda t E[N(t)]=λt
复合泊松过程的均值:
复合泊松过程的均值通过以下公式计算:
E [ Y ( t ) ] = E [ ∑ k = 1 N ( t ) X k ] \mathbb{E}[Y(t)] = \mathbb{E}\left[ \sum_{k=1}^{N(t)} X_k \right] E[Y(t)]=E k=1∑N(t)Xk
由于 ( X_k ) 是独立同分布的,因此可以利用条件期望的性质:
E [ Y ( t ) ] = E [ N ( t ) ] ⋅ E [ X k ] \mathbb{E}[Y(t)] = \mathbb{E}[N(t)] \cdot \mathbb{E}[X_k] E[Y(t)]=E[N(t)]⋅E[Xk]
我们需要知道随机变量 ( X_k ) 的均值 ( \mathbb{E}[X_k] )。假设 ( X_k ) 的概率密度函数 ( f(x) ) 已知,那么我们可以通过以下积分计算期望:
E [ X k ] = ∫ a b x f ( x ) d x \mathbb{E}[X_k] = \int_{a}^{b} x f(x) dx E[Xk]=∫abxf(x)dx
在本例中,假设 ( f(x) ) 为均匀分布,计算结果为:
E [ X k ] = 1500 \mathbb{E}[X_k] = 1500 E[Xk]=1500
因此,复合泊松过程的均值为:
E [ Y ( t ) ] = 7500 t \mathbb{E}[Y(t)] = 7500t E[Y(t)]=7500t
方差推导
复合泊松过程的方差公式为:
Var ( Y ( t ) ) = E [ N ( t ) ] ⋅ Var ( X k ) \text{Var}(Y(t)) = \mathbb{E}[N(t)] \cdot \text{Var}(X_k) Var(Y(t))=E[N(t)]⋅Var(Xk)
我们已经知道泊松过程的期望 ( E [ N ( t ) ] = 5 t ( \mathbb{E}[N(t)] = 5t (E[N(t)]=5t)。接下来,我们需要计算 ( X_k ) 的方差。
随机变量 ( X_k ) 的方差:
复合泊松过程的方差为:
Var [ Y ( t ) ] = λ t E [ X 2 ] . \text{Var}[Y(t)] = \lambda t \mathbb{E}[X^2]. Var[Y(t)]=λtE[X2].
$$
具体推导可以看我的另一篇文章。
接下来计算 E [ X 2 ] \mathbb{E}[X^2] E[X2]
E [ X 2 ] = ∫ a b x 2 f ( x ) d x \mathbb{E}[X^2] = \int_{a}^{b} x^2 f(x) dx E[X2]=∫abx2f(x)dx
什么是特征函数?
特征函数(Characteristic Function)是描述随机变量分布的一种工具,它可以捕捉随机变量的全部统计信息。特征函数定义为:
φ X ( t ) = E [ e i t X ] \varphi_X(t) = \mathbb{E}[e^{itX}] φX(t)=E[eitX]
其中,( t ) 是实数,( i ) 是虚数单位 ( i = − 1 ( i = \sqrt{-1} (i=−1),而 ( X ) 是一个随机变量。
特征函数的重要性质
-
唯一性:特征函数唯一确定一个随机变量的分布。如果两个随机变量的特征函数相同,它们的分布也是相同的。
-
求和性质:若 ( X_1 ) 和 ( X_2 ) 是两个独立随机变量,则它们和的特征函数为:
φ X 1 + X 2 ( t ) = φ X 1 ( t ) ⋅ φ X 2 ( t ) \varphi_{X_1 + X_2}(t) = \varphi_{X_1}(t) \cdot \varphi_{X_2}(t) φX1+X2(t)=φX1(t)⋅φX2(t)
-
期望与方差:特征函数的导数可以用于计算期望和方差。若特征函数在 ( t = 0 ) 处可导,则:
- 期望: E [ X ] = i d d t φ X ( t ) ∣ t = 0 \mathbb{E}[X] = i \frac{d}{dt} \varphi_X(t) \Big|_{t=0} E[X]=idtdφX(t) t=0
- 方差: Var ( X ) = − d 2 d t 2 φ X ( t ) ∣ t = 0 \text{Var}(X) = -\frac{d^2}{dt^2} \varphi_X(t) \Big|_{t=0} Var(X)=−dt2d2φX(t) t=0
-
总是存在:无论随机变量的分布是什么,它的特征函数总是存在,因为对于任意 ( X ), ( e i t X ( e^{itX} (eitX) 的期望是有限的。
特征函数的例子
-
正态分布的特征函数:对于均值为 ( μ ( \mu (μ) ,方差为 ( σ 2 ( \sigma^2 (σ2) 的正态分布 ( X ∼ N ( μ , σ 2 ) ( X \sim \mathcal{N}(\mu, \sigma^2) (X∼N(μ,σ2)),特征函数为:
φ X ( t ) = exp ( i t μ − 1 2 σ 2 t 2 ) \varphi_X(t) = \exp\left(it\mu - \frac{1}{2}\sigma^2 t^2\right) φX(t)=exp(itμ−21σ2t2)
-
泊松分布的特征函数:对于参数为 ( λ ( \lambda (λ) 的泊松分布 ( X ∼ Poisson ( λ ) ( X \sim \text{Poisson}(\lambda) (X∼Poisson(λ)),特征函数为:
φ X ( t ) = exp ( λ ( e i t − 1 ) ) \varphi_X(t) = \exp\left(\lambda (e^{it} - 1)\right) φX(t)=exp(λ(eit−1))
应用
特征函数在概率论中有广泛的应用:
- 求解独立随机变量和的分布:通过特征函数的乘积性质,可以很方便地计算独立随机变量的和的分布。
- 极限理论:在证明中心极限定理时,特征函数是一个非常有用的工具。
- 简化复杂计算:特征函数在处理随机变量的卷积或变换时,提供了简洁的计算方式。
总结
通过复合泊松过程的均值和方差推导,我们可以更清晰地理解这一随机过程的统计性质。特征函数作为概率论中的重要工具,不仅能帮助我们描述随机变量的分布,还可以通过它的性质简化许多复杂的概率计算。了解这些概念对于深入掌握概率论中的随机过程非常有帮助。
相关文章:

复合泊松过程
复合泊松过程的均值、方差与特征函数 复合泊松过程的定义 复合泊松过程 ( Y(t) ) 是一种常见的随机过程,通常定义为: Y ( t ) ∑ k 1 N ( t ) X k Y(t) \sum_{k1}^{N(t)} X_k Y(t)k1∑N(t)Xk 其中: ( N(t) ) 是一个强度为 ( \lambd…...

[week1] newstar ctf ezAndroidStudy
本题主要考查对 APK 基本结构的掌握 查看 AndroidManifest.xml 可以发现 activity 只有 Homo 和 MainActivity 我们用 Jadx 打开 work.pangbai.ezandroidstudy.Homo 就可以获得 flag1 打开 resources.arsc/res/value/string.xml 搜索 flag2 即可 按描述到 /layout/activity_ma…...

TCP——Socket
应用进程只借助Socket API发和收但是不关心他是怎么进行传和收的 数据结构 图示Socket连接 捆绑属于隐式捆绑...
)
OpenStack服务Swift重启失效(已解决)
案例分析Swift重启失效 1. 报错详情 在重新启动 VMware 虚拟机后,我们发现 OpenStack 的 Swift 服务出现了 503 Service Unavailable 错误。经过排查,问题根源在于 Swift 服务所使用的存储挂载是临时挂载,而非永久挂载。 Swift 服务依赖于…...

System.Text.Json类库进行json转化时ValueKind:Object问题
当你的使用的Json库是System.Text.Json,而不是Newtonsoft.Json库的时候,你可能遇到以下问题及其解决办法。通常的解决办法是进行一些对应的配置。此外就需要根据情况使用自定义转换器实现你的需求。以下是通常遇到的使用自定义转换器解决的例子: Q1.当遇…...

免费Excel工作表同类数据合并工具
下载地址:https://pan.quark.cn/s/81b1aeb45e4c 在 Excel 表格里,当我们试图手动将多行同类数据合并为一行时,会遭遇诸多棘手的困难以及繁杂的操作流程。在确定哪些数据属于可合并的同类数据时,单纯依靠人工进行对比,极…...

如何在算家云搭建Video-Infinity(视频生成)
一、模型介绍 Video-Infinity是一个先进的视频生成模型,使用多个 GPU 快速生成长视频,无需额外训练。它能够基于用户提供的文本或图片提示,创造出高质量、多样化的视频内容。 二、模型搭建流程 1.大模型 Video-Infinity 一键使用 基础环境…...

LeetCode搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 示例 1: 输入: nums [1,3,5,6], target 5 输出: 2 …...

UE5学习笔记24-添加武器弹药
一、给角色的武器添加弹药 1.创建界面,根据笔记23的界面中添加 2.绑定界面控件 UPROPERTY(meta (Bindwidget))UTextBlock* WeaponAmmoAmount;UPROPERTY(meta (Bindwidget))UTextBlock* CarriedAmmoAmount; 3.添加武器类型枚举 3.1创建武器类型枚举头文件 3.2创建文…...

限制游客在wordpress某分类下阅读文章的数量
在WordPress中实现某个分类下的内容限制游客只能阅读前5篇文章,注册用户可以阅读更多文章的功能,可以通过以下步骤来完成: 1. 安装和激活插件 首先,你可以使用一个插件来简化这个过程。一个常用的插件是 “MemberPress” 或 “R…...

Oracle云主机申请和使用教程:从注册到SSH连接的全过程
今天我要和大家分享如何成功申请Oracle云主机,并进行基本的配置和使用。我知道很多同行的朋友在申请Oracle云主机时都遇到了困难(疑惑abc错误),可能试了很多次都没有成功。现总结一下这些年来的一些注册流程经验,或许你们也能成功申请到自己的…...

芯知识 | NVH-FLASH语音芯片支持平台做语音—打造音频IC技术革新
随着科技的飞速发展,人们对于电子产品的音频性能要求越来越高。在这种背景下,NVH-FLASH系列语音芯片应运而生,作为音频IC领域的一次重大技术革新,NVH-FLASH系列语音芯片凭借其卓越的性能与灵活的支持平台,正逐步引领着…...

机器学习——解释性AI与可解释性机器学习
解释性AI与可解释性机器学习: 理解机器学习模型背后的逻辑 随着人工智能技术的广泛应用,机器学习模型越来越多地被用于决策过程。然而,这些模型,尤其是深度学习模型,通常被视为“黑箱”,难以理解其背后的决策逻辑。解…...

中国全国省市区县汇总全国省市区json省市区数据2024最新
简介 包含全国省市区县数据,共3465个。 全国总共有23个省、5个自治区、4个直辖市、2个特别行政区。 ——更新于2024年10月16日,从2017年开始,已经更新坚持7年 从刚开始1000个左右的城市json,到现在全国省市区县3465个。 本人感觉应该是目前最完善的~ 每年都在更新中,…...
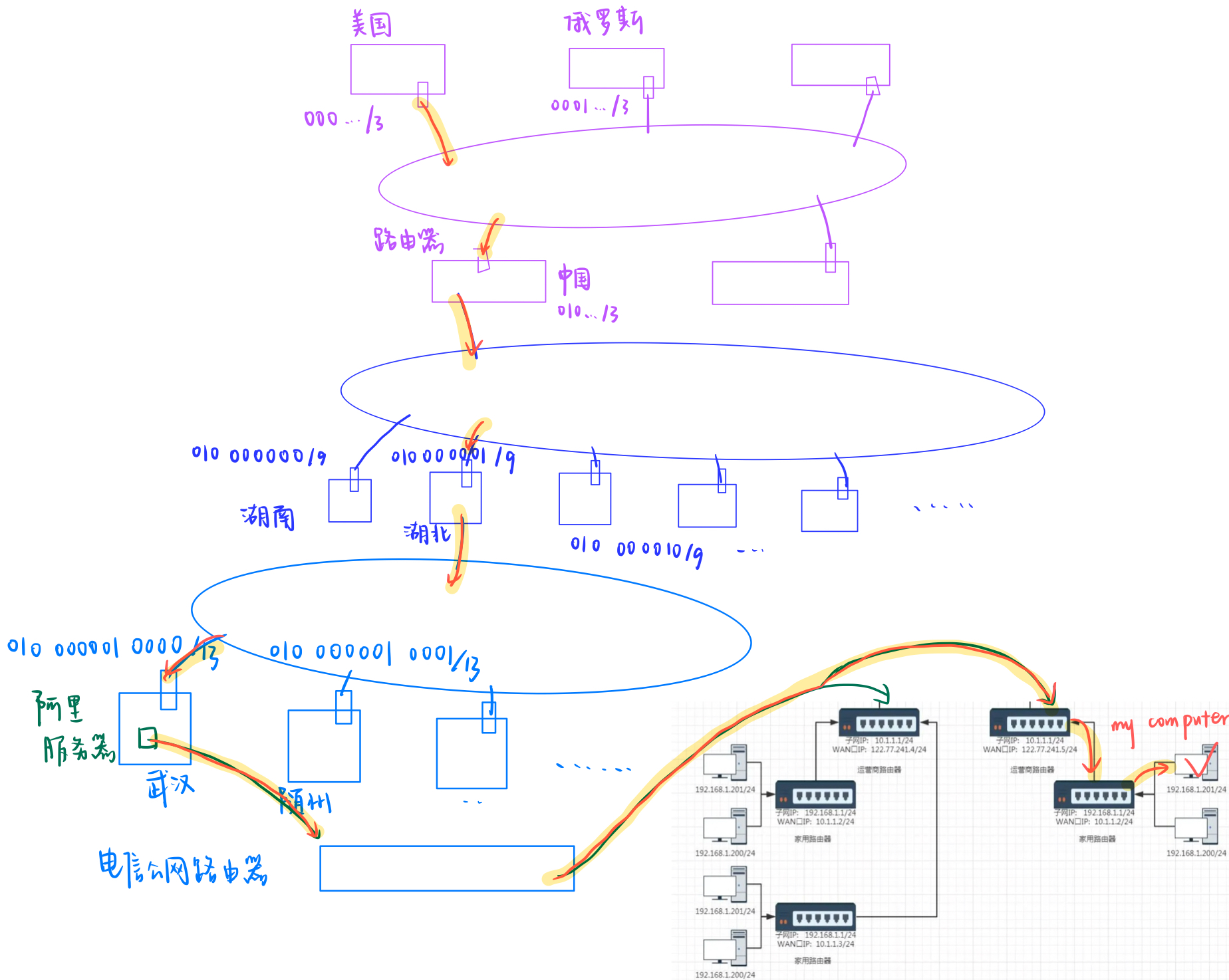
[Linux#67][IP] 报头详解 | 网络划分 | CIDR无类别 | DHCP动态分配 | NAT转发 | 路由器
目录 一. IP协议头格式 学习任何协议前的两个关键问题 IP 报头与有效载荷分离 分离方法 为什么需要16位总长度 如何交付 二. 网络通信 1.IP地址的划分理念 2. 子网管理 3.网络划分 CIDR(无类别域间路由) 目的IP & 当前路由器的子网掩码 …...

路由器原理和静态路由配置
一、路由器的工作原理 根据路由表转发数据 接收数据包→查看目的地址→与路由表进行匹配找到转发端口→转发到该端口 二、路由表的形成 它是路由器中维护的路由条目的集合,路由器根据路由表做路径选择,里面记录了网段ip地址和对应下一跳接口的接口号。…...

UE5 使用Animation Budget Allocator优化角色动画性能
Animation Budget Allocator是UE内置插件,通过锁定动画系统所占CPU的预算,在到达预算计算量时对动画进行限制与优化。 开启Animation Budget Allocator需要让蒙皮Mesh使用特定的组件,并进行一些编辑器设置即可开启。 1.开启Animation Budget…...

Element UI 组件库详解:从入门到精通
在追求统一且流畅的用户体验时,开发者们常常选择使用 UI 组件库来加快开发速度。Element UI,这个基于 Vue.js 的组件库,提供了大量界面组件,极大地提升了前端开发的效率。本文将指导您如何开始使用 Element UI 组件库,…...

JavaScript 事件循环(EventLoop) —— 浏览器 Node
一、事件循环的本质 本质:运行时对 JS 脚本的调度方式就叫做事件循环. 对于 浏览器 而言,需要考虑用户交互、UI渲染、脚本运行、网络请求等操作,这些操作必然都依赖于事件去执行,因此,为了协调事件必须要使用事件循环…...

【ROS2】订阅手柄数据,发布运动命令
1、相关消息 sensor_msgs::msg::Joy:用来描述手柄控制器数据 geometry_msgs::msg::Twist :用来描述物体运动时的线速度和角速度 参见博客: 【ROS2】geometry_msgs::msg::Twist和sensor_msgs::msg::Joy 2、订阅和发布 2.1 定义、创建订阅者和发布者 订阅手柄的按键、摇杆…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...
