算法题总结（十四）——贪心算法（上）

贪心算法

什么是贪心

贪心的本质是选择每一阶段的局部最优，从而达到全局最优。

贪心的套路（什么时候用贪心）

刷题或者面试的时候，手动模拟一下感觉可以局部最优推出整体最优，而且想不到反例，那么就试一试贪心

455、分发饼干

假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。

对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

示例 1:

输入: g = [1,2,3], s = [1,1]
输出: 1
解释: 
你有三个孩子和两块小饼干，3个孩子的胃口值分别是：1,2,3。
虽然你有两块小饼干，由于他们的尺寸都是1，你只能让胃口值是1的孩子满足。
所以你应该输出1。

大尺寸的饼干既可以满足胃口大的孩子也可以满足胃口小的孩子，那么就应该优先满足胃口大的。

这里的局部最优就是大饼干喂给胃口大的，充分利用饼干尺寸喂饱一个，全局最优就是喂饱尽可能多的小孩。

class Solution {// 思路1：优先考虑饼干，小饼干先喂饱小胃口，因为如果大饼干先喂大胃口，则不能尽可能多的喂public int findContentChildren(int[] g, int[] s) {Arrays.sort(g);Arrays.sort(s);int start = 0; //胃口序号int count = 0;for (int i = 0; i < s.length && start < g.length; i++) {if (s[i] >= g[start]) {start++;count++;}}return count;}
}

class Solution {// 思路2：优先考虑胃口，先喂饱大胃口public int findContentChildren(int[] g, int[] s) {Arrays.sort(g);Arrays.sort(s);int count = 0;int start = s.length - 1;// 遍历胃口for (int index = g.length - 1; index >= 0; index--) {if(start >= 0 && g[index] <= s[start]) {start--;count++;}}return count;}
}

376、摆动序列

如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为 摆动序列 。第一个差（如果存在的话）可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。

• 例如， [1, 7, 4, 9, 2, 5] 是一个 摆动序列 ，因为差值 (6, -3, 5, -7, 3) 是正负交替出现的。
• 相反，[1, 4, 7, 2, 5] 和 [1, 7, 4, 5, 5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。

子序列 可以通过从原始序列中删除一些（也可以不删除）元素来获得，剩下的元素保持其原始顺序。

给你一个整数数组 nums ，返回 nums 中作为 摆动序列 的 最长子序列的长度 。

示例 1：

输入：nums = [1,7,4,9,2,5]
输出：6
解释：整个序列均为摆动序列，各元素之间的差值为 (6, -3, 5, -7, 3) 。

示例 2：

输入：nums = [1,17,5,10,13,15,10,5,16,8]
输出：7
解释：这个序列包含几个长度为 7 摆动序列。
其中一个是 [1, 17, 10, 13, 10, 16, 8] ，各元素之间的差值为 (16, -7, 3, -3, 6, -8) 。

局部最优：删除单调坡度上的节点（不包括单调坡度两端的节点），那么这个坡度就可以有两个局部峰值。

整体最优：整个序列有最多的局部峰值，从而达到最长摆动序列。

实际操作上，其实连删除的操作都不用做，因为题目要求的是最长摆动子序列的长度，所以只需要统计数组的峰值数量就可以了（相当于是删除单一坡度上的节点，然后统计长度）

这就是贪心所贪的地方，让峰值尽可能的保持峰值，然后删除单一坡度上的节点

所以我们只需要统计峰值的数目就可以的。

在计算是否有峰值的时候，大家知道遍历的下标 i ，计算 prediff（nums[i] - nums[i-1]） 和 curdiff（nums[i+1] - nums[i]），如果prediff < 0 && curdiff > 0 或者 prediff > 0 && curdiff < 0 此时就有波动就需要统计。

这是我们思考本题的一个大题思路，但本题要考虑三种情况：

1. 情况一：上下坡中有平坡
2. 情况二：数组首尾两端
3. 情况三：单调坡中有平坡

情况一：上下坡中有平坡

例如 [1,2,2,2,1]这样的数组，如图：

如图，可以统一规则，删除左边的三个 2：

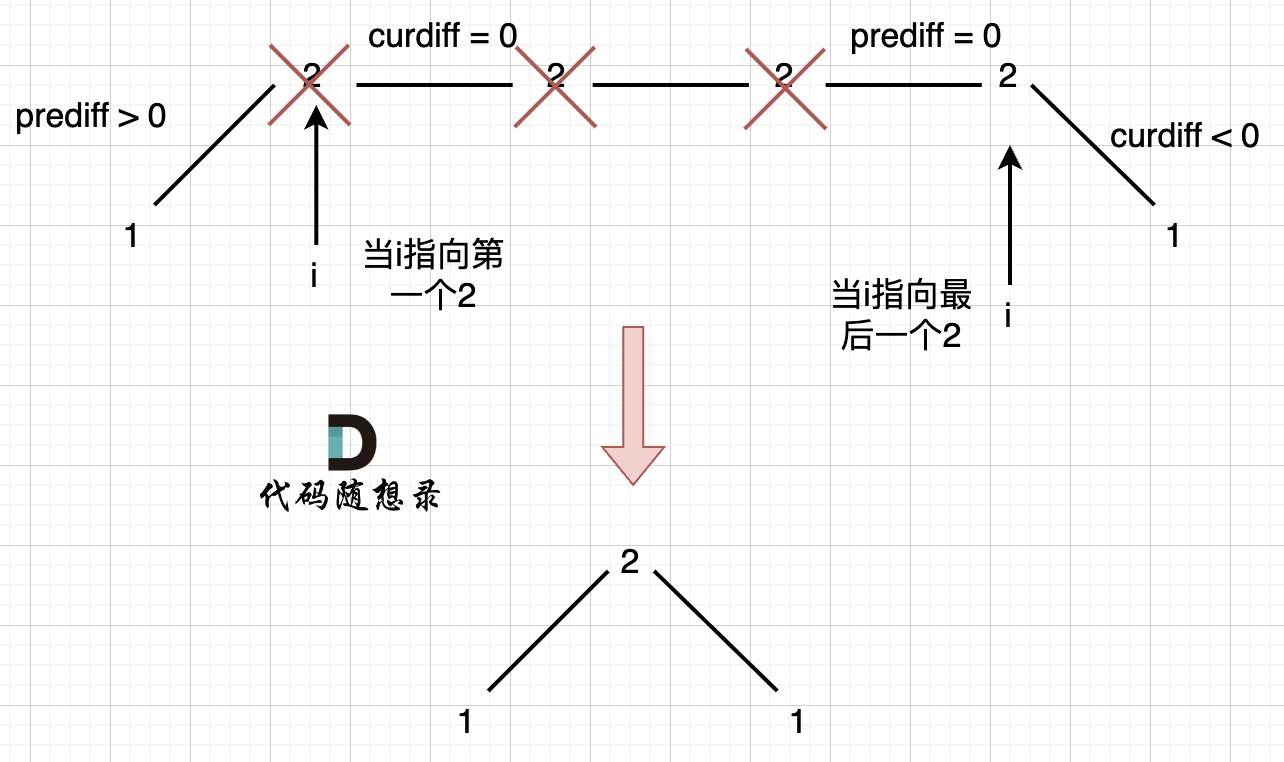
如果我们采用，删左面三个 2 的规则，那么 当 prediff = 0 && curdiff < 0 也要记录一个峰值，因为他是把之前相同的元素都删掉留下的峰值。

所以我们记录峰值的条件应该是： (preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)，为什么这里允许 prediff == 0 ，就是为了 上面我说的这种情况。

情况二：数组首尾两端

针对数组中只有两个数字的怎么计算？

利用 prediff的初始值为0，result 初始为 1（默认最右面有一个峰值），这样就可以利用(preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)来判断，那么 result++（计算了左面的峰值），最后得到的 result 就是 2（峰值个数为 2 即摆动序列长度为 2）

情况三：单调坡度有平坡

在版本一中，我们忽略了一种情况，即 如果在一个单调坡度上有平坡，例如[1,2,2,2,3,4]，如图：

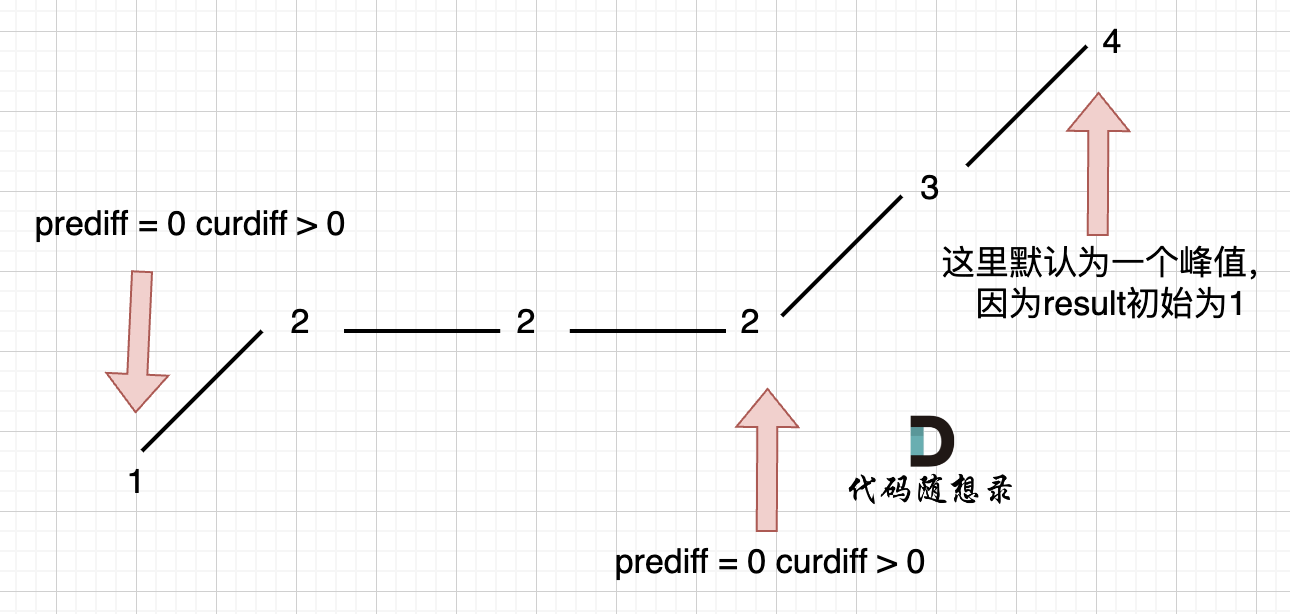
图中，我们可以看出，版本一的代码在三个地方记录峰值，但其实结果因为是 2，因为 单调中的平坡 不能算峰值（即摆动）。

之所以版本一会出问题，是因为我们实时更新了 prediff。

那么我们应该什么时候更新 prediff 呢？

我们只需要在 这个坡度 摆动变化的时候，更新 prediff 就行，这样 prediff 在 单调区间有平坡的时候 就不会发生变化，造成我们的误判。

class Solution {public int wiggleMaxLength(int[] nums) {if (nums.length <= 1) {return nums.length;}//当前差值int curDiff = 0;//上一个差值int preDiff = 0;   //默认差值int count = 1;    //默认最右端有一个峰值for (int i = 1; i < nums.length; i++) {//得到当前差值curDiff = nums[i] - nums[i - 1];//如果当前差值和上一个差值为一正一负//等于0的情况表示初始时的preDiffif ((preDiff>=0&&curDiff<0)|| (preDiff<=0&&curDiff>0)) {count++;preDiff = curDiff;}}return count;}
}

时间复杂度O（n）

思路 2（动态规划）

考虑用动态规划的思想来解决这个问题。

很容易可以发现，对于我们当前考虑的这个数，要么是作为山峰（即 nums[i] > nums[i-1]），要么是作为山谷（即 nums[i] < nums[i - 1]）。

• 设 dp 状态dp[i][0]，表示考虑前 i 个数，第 i 个数作为山峰的摆动子序列的最长长度
• 设 dp 状态dp[i][1]，表示考虑前 i 个数，第 i 个数作为山谷的摆动子序列的最长长度

则转移方程为：

• dp[i][0] = max(dp[i][0], dp[j][1] + 1)，其中0 < j < i且nums[j] < nums[i]，表示将 nums[i]接到前面某个山谷后面，作为山峰。
• dp[i][1] = max(dp[i][1], dp[j][0] + 1)，其中0 < j < i且nums[j] > nums[i]，表示将 nums[i]接到前面某个山峰后面，作为山谷。

初始状态：

由于一个数可以接到前面的某个数后面，也可以以自身为子序列的起点，所以初始状态为：dp[0][0] = dp[0][1] = 1。

// DP
class Solution {public int wiggleMaxLength(int[] nums) {// 0 i 作为波峰的最大长度// 1 i 作为波谷的最大长度int dp[][] = new int[nums.length][2];dp[0][0] = dp[0][1] = 1;for (int i = 1; i < nums.length; i++){//i 自己可以成为波峰或者波谷dp[i][0] = dp[i][1] = 1;   //即dp最小值就是1for (int j = 0; j < i; j++){if (nums[j] > nums[i]){// i 是波谷dp[i][1] = Math.max(dp[i][1], dp[j][0] + 1);}if (nums[j] < nums[i]){// i 是波峰dp[i][0] = Math.max(dp[i][0], dp[j][1] + 1);}}}return Math.max(dp[nums.length - 1][0], dp[nums.length - 1][1]);}
}

53、最大子数组和

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组 是数组中的一个连续部分。

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

示例 2：

输入：nums = [1]
输出：1

贪心贪的是哪里呢？

如果 -2 1 在一起，计算起点的时候，一定是从 1 开始计算，因为负数只会拉低总和，这就是贪心贪的地方！

局部最优：当前“连续和”为负数的时候立刻放弃，从下一个元素重新计算“连续和”，因为负数加上下一个元素 “连续和”只会越来越小。

全局最优：选取最大“连续和”

局部最优的情况下，并记录最大的“连续和”，可以推出全局最优。

从代码角度上来讲：遍历 nums，从头开始用 count 累积，如果 count 一旦加上 nums[i]变为负数，那么就应该从 nums[i+1]开始从 0 累积 count 了，因为已经变为负数的 count，只会拖累总和。区间终止位置，其实就是用sum来记录了最大值。

累加，并记录累加的和，一旦count变成负数，就应该重新计算。

class Solution {public int maxSubArray(int[] nums) {if (nums.length == 1){return nums[0];}int sum = Integer.MIN_VALUE;int count = 0;for (int i = 0; i < nums.length; i++){count += nums[i];sum = Math.max(sum, count); // 取区间累计的最大值（相当于不断确定最大子序终止位置）//每次都要先判断sum，然后再判断count。比如-1，-1，-1，-1，-1if (count <= 0){count = 0; // 相当于重置最大子序起始位置，因为遇到负数一定是拉低总和}}return sum;}
}

动态规划方法：

// DP 方法
class Solution {public int maxSubArray(int[] nums) {int ans = Integer.MIN_VALUE;int[] dp = new int[nums.length];  //表示以i结尾的 子序列的最大和dp[0] = nums[0];ans = dp[0];    //记录最大值for (int i = 1; i < nums.length; i++){dp[i] = Math.max(dp[i-1] + nums[i], nums[i]);ans = Math.max(dp[i], ans);}return ans;}
}

121、买卖股票的最佳时机

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

示例 1：

输入：[7,1,5,3,6,4]
输出：5
解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

示例 2：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 没有交易完成, 所以最大利润为 0。

提示：

• 1 <= prices.length <= 105
• 0 <= prices[i] <= 104

本题注意，这一支股票只能买卖一次！所以要选取最大的差值。

所以使用贪心算法，遍历一次，分别找前面的最小值，和最大的差值！

class Solution {public int maxProfit(int[] prices) {int min=Integer.MAX_VALUE;int result=0;for(int i=0;i<prices.length;i++){min=Math.min(min,prices[i]);  //寻找前面的最小值result=Math.max(result,prices[i]-min);  //最大差值}return result;}
}

动态规划：

class Solution {public int maxProfit(int[] prices) {int len =prices.length;//dp[i][0]代表第i天的时候持有股票，的最大收益//dp[i][1]代表第i天不持有股票的最大收益int[][] dp=new int[len][2];dp[0][0]=-prices[0];dp[0][1]=0;for(int i=1;i<len;i++){dp[i][0]=Math.max(dp[i-1][0],-prices[i]);dp[i][1]=Math.max(dp[i-1][0]+prices[i],dp[i-1][1]);}return dp[len-1][1];}
}

122、买卖股票的最佳时机 II

给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。

在每一天，你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买，然后在 同一天 出售。

返回 你能获得的 最大 利润 。

示例 1：

输入：prices = [7,1,5,3,6,4]
输出：7
解释：在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3 。总利润为 4 + 3 = 7 。

示例 2：

输入：prices = [1,2,3,4,5]
输出：4
解释：在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。总利润为 4 。

此题与上一题不同的就是 这一支股票可以买卖多次！，然后算出来总利润！

如果想到其实最终利润是可以分解的，那么本题就很容易了！

如何分解呢？

假如第 0 天买入，第 3 天卖出，那么利润为：prices[3] - prices[0]。

相当于(prices[3] - prices[2]) + (prices[2] - prices[1]) + (prices[1] - prices[0])。

此时就是把利润分解为每天为单位的维度，而不是从 0 天到第 3 天整体去考虑！

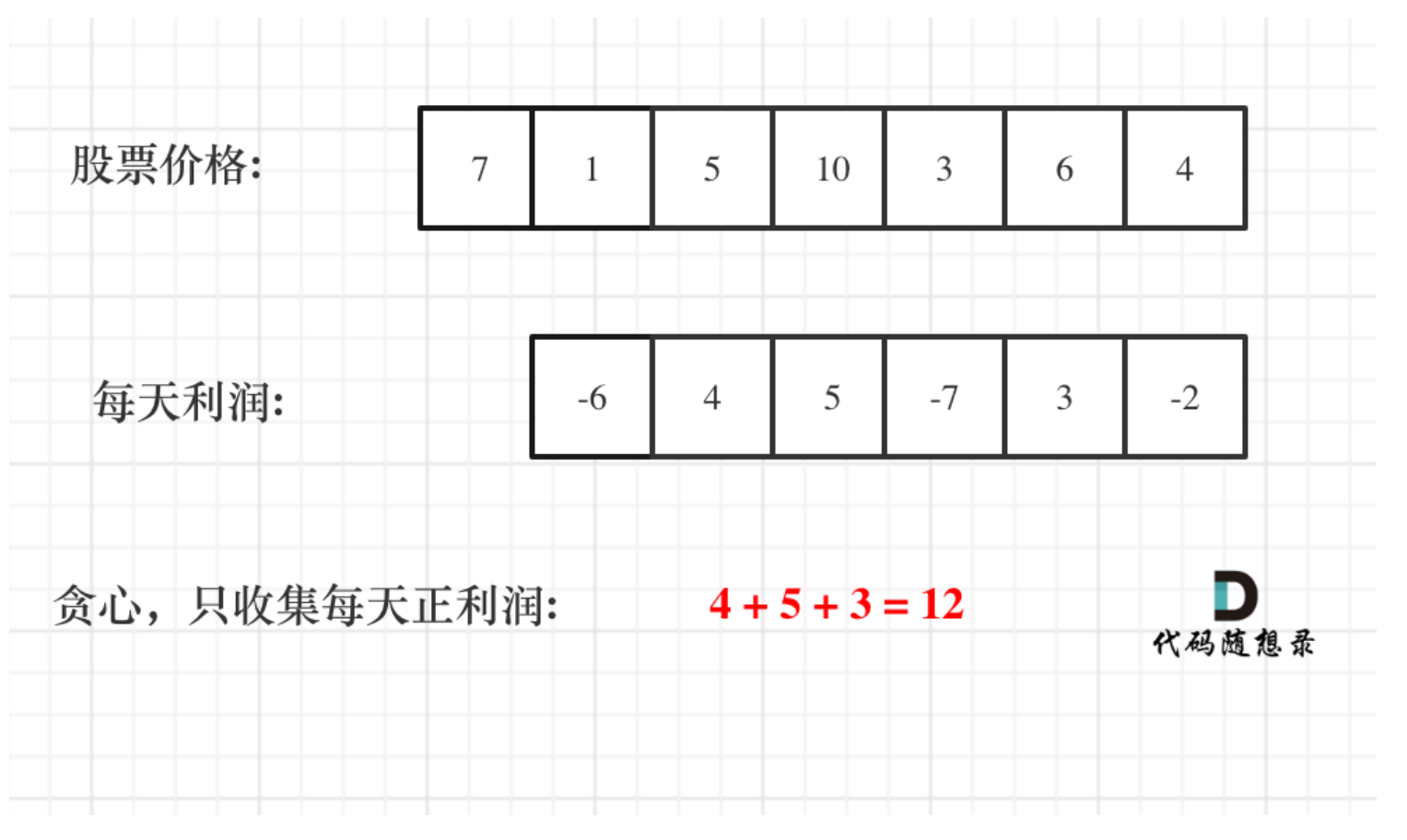
局部最优：收集每天的正利润，全局最优：求得最大利润。

因为可以当天卖出后又买入，相当于没有卖出。

class Solution {public int maxProfit(int[] prices) {//数组记录利润int[] profit=new int[prices.length-1];int result=0;for(int i=0;i<prices.length-1;i++){profit[i]=prices[i+1]-prices[i];}for(int i=0;i<profit.length;i++){if(profit[i]>0)result+=profit[i];}return result;}
}

55、跳跃游戏

给你一个非负整数数组 nums ，你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个下标，如果可以，返回 true ；否则，返回 false 。

示例 1：

输入：nums = [2,3,1,1,4]
输出：true
解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。

示例 2：

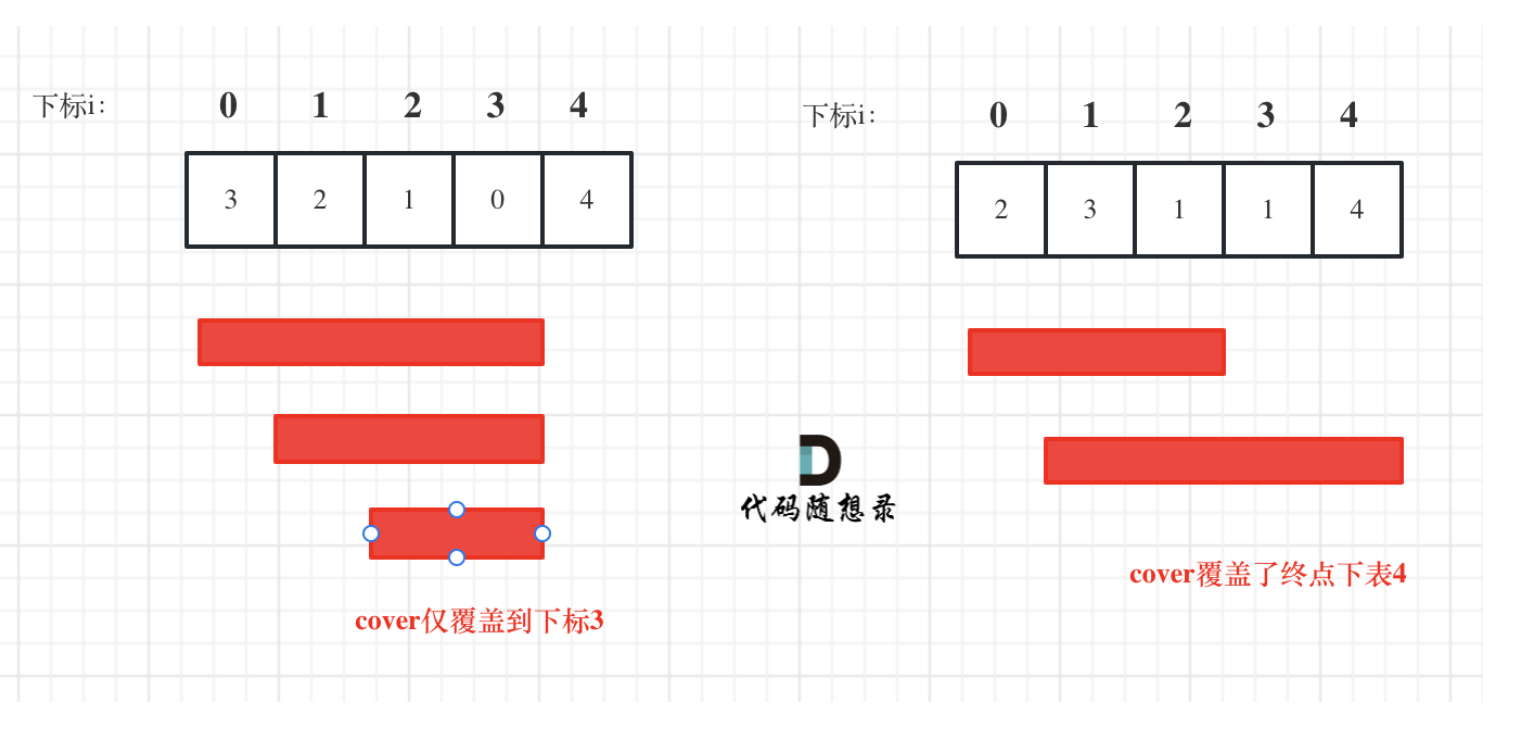
输入：nums = [3,2,1,0,4]
输出：false
解释：无论怎样，总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 ， 所以永远不可能到达最后一个下标。

其实跳几步无所谓，关键在于可跳的覆盖范围！

那么这个问题就转化为跳跃覆盖范围究竟可不可以覆盖到终点！

贪心算法局部最优解：每次取最大跳跃步数（取最大覆盖范围），整体最优解：最后得到整体最大覆盖范围，看是否能到终点。

class Solution {public boolean canJump(int[] nums) {if(nums.length==1)return true;//初试覆盖范围int coverRange=nums[0];//在覆盖范围内更新最大的覆盖范围for(int i=0;i<=coverRange;i++)   //for循环中的最大覆盖范围是一个变量{coverRange=Math.max(coverRange,i+nums[i]);if(coverRange>=nums.length-1)return true;}return false;}
}

45、跳跃游戏 II

给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。

每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说，如果你在 nums[i] 处，你可以跳转到任意 nums[i + j] 处:

• 0 <= j <= nums[i]
• i + j < n

返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。

示例 1:

输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。

示例 2:

输入: nums = [2,3,0,1,4]
输出: 2

本题和55思路是相似的，还是要看最大覆盖范围。

即局部最优：当前覆盖范围内尽可能多走，如果还没到终点，步数再加一。整体最优：一步尽可能多走，从而达到最少步数。

即看每步的最大覆盖范围，每个覆盖范围是一步。

class Solution {public int jump(int[] nums) {if(nums.length==1)return 0;//根据覆盖范围来计算 每个范围是一步int coverRange = nums[0];   //当前这一步的覆盖范围int count=1;int maxRange=nums[0];     //从当前范围再走一步能到的最大范围，即下一步的最大覆盖for(int i=0;i<=coverRange;i++){maxRange=Math.max(maxRange,i+nums[i]); //不断更新下一步的最大覆盖if(coverRange>=nums.length-1)  //如果当前覆盖距离能到{return count;}if(maxRange>=nums.length-1)   //下一个范围才能覆盖到{count++;return count;}if(i==coverRange)   //在此范围内的最大距离到不了终点，即走到了这一步范围的终点{coverRange=maxRange;  //coverRange更新后不会跳出循环count++;}}return count;}
}