python 不相交集简介(并查集算法)【Introduction to Disjoint Set (Union-Find Algorithm)】

什么是不相交集数据结构?
如果两个集合没有任何共同元素,则它们被称为不相交集,集合的交集为空集。
存储不重叠或不相交元素子集的数据结构称为不相交集合数据结构。不相交集合数据结构支持以下操作:
1、将新集合添加到不相交集合中。
2、使用联合操作将不相交集合并为单个不相交集。
3、使用“查找”操作查找不相交集的代表。
4、检查两个集合是否不相交。
考虑这样一个情况,有许多人需要执行以下任务:
1、添加新的友谊关系,即一个人 x 成为另一个人 y 的朋友,即向集合中添加新元素。
2、判断个体x 是否是个体 y 的朋友(直接或间接朋友)
例子:
我们有 10 个人,比如 a、b、c、d、e、f、g、h、i、j
以下是需要添加的关系:
a <-> b
b <-> d
c <-> f
c <-> i
j <-> e
g <-> j
给定查询,例如 a 是否是 d 的朋友。我们基本上需要创建以下 4 个组,并在组项之间保持快速访问的连接:
G1 = {a, b, d}
G2 = {c, f, i}
G3 = {e, g, j}
G4 = {h}
判断 x 和 y 是否属于同一组,即判断 x 和 y 是否是直接/间接朋友。
根据个体所属的组别,将个体划分为不同的集合。此方法称为不相交集合并集,它维护不相交集合的集合,每个集合由其成员之一表示。
要回答上述问题,需要考虑两个关键点:
1、如何解析集合?最初,所有元素都属于不同的集合。在处理给定的关系后,我们选择一个成员作为代表。选择代表的方法有很多种,一种简单的方法是选择最大的索引。
2、检查两个人是否在同一组中?如果两个人的代表相同,那么他们就会成为朋友。
使用的数据结构包括:
数组:整数数组称为Parent[]。如果我们处理N 个项目,则数组的第 i 个元素代表第 i 个项目。更准确地说,Parent[] 数组的第 i 个元素是第 i 个项目的父级。这些关系创建一个或多个虚拟树。
树:它是一个不相交集。如果两个元素在同一棵树中,那么它们就在同一个不相交集。每棵树的根节点(或最顶端节点)称为集合的代表。每个集合始终有一个唯一的代表。识别代表的一个简单规则是,如果“i”是集合的代表,则Parent[i] = i。如果 i 不是其集合的代表,则可以通过沿树向上移动直到找到代表来找到它。
不相交集合数据结构上的操作:
查找
联合
1. 查找:
可以通过递归遍历父数组直到找到其自身的父节点来实现。
# Finds the representative of the set
# that i is an element of
def find(i):
# If i is the parent of itself
if (parent[i] == i):
# Then i is the representative of
# this set
return i
else:
# Else if i is not the parent of
# itself, then i is not the
# representative of his set. So we
# recursively call Find on its parent
return find(parent[i])
# The code is contributed by Nidhi goel
时间复杂度:这种方法效率低下,在最坏的情况下可能需要 O(n) 时间。
2. 联合:
它以两个元素作为输入,并使用查找操作找到它们的集合的代表,最后将其中一棵树(代表集合)放在另一棵树的根节点下。
# Unites the set that includes i
# and the set that includes j
def union(parent, rank, i, j):
# Find the representatives
# (or the root nodes) for the set
# that includes i
irep = find(parent, i)
# And do the same for the set
# that includes j
jrep = find(parent, j)
# Make the parent of i’s representative
# be j’s representative effectively
# moving all of i’s set into j’s set)
parent[irep] = jrep
时间复杂度:这种方法效率低下,在最坏的情况下可能导致长度为 O(n)的树。
优化(按等级/大小合并和路径压缩):
效率在很大程度上取决于哪棵树连接到另一棵树。有两种方法可以实现。第一种是按等级联合,它将树的高度视为一个因素;第二种是按大小联合,它将树的大小视为一个因素,同时将一棵树连接到另一棵树。此方法与路径压缩一起提供了几乎恒定时间的复杂性。
路径压缩(对 Find() 的修改):
它通过压缩树的高度来加速数据结构。这可以通过在Find操作中插入一个小的缓存机制来实现。查看代码了解更多详细信息:
# Finds the representative of the set that i
# is an element of.
def find(i):
# If i is the parent of itself
if Parent[i] == i:
# Then i is the representative
return i
else:
# Recursively find the representative.
result = find(Parent[i])
# We cache the result by moving i’s node
# directly under the representative of this
# set
Parent[i] = result
# And then we return the result
return result
# The code is contributed by Arushi Jindal.
时间复杂度:平均每次调用为 O(log n)。
按等级合并:
首先,我们需要一个新的整数数组,名为rank[] 。此数组的大小与父数组Parent[]相同。如果 i 代表一个集合,则rank[i]就是代表该集合的树的高度。 现在回想一下,在 Union 操作中,将两棵树中的哪一棵移动到另一棵之下并不重要。现在我们要做的是最小化结果树的高度。如果我们要合并两棵树(或集合),我们将它们称为左和右,那么这一切都取决于左的等级和右的等级。
1、如果左边的等级小于右边的等级,那么最好将左边移到右边的下方,因为这不会改变右边的等级(而将右边移到左边的下方会增加高度)。同样,如果右边的等级小于左边的等级,那么我们应该将右边移到左边的下方。
2、如果等级相等,那么哪棵树位于另一棵树之下并不重要,但结果的等级始终比树的等级大一。
class DisjointSet:
def __init__(self, size):
self.parent = [i for i in range(size)]
self.rank = [0] * size
# Function to find the representative (or the root node) of a set
def find(self, i):
# If i is not the representative of its set, recursively find the representative
if self.parent[i] != i:
self.parent[i] = self.find(self.parent[i]) # Path compression
return self.parent[i]
# Unites the set that includes i and the set that includes j by rank
def union_by_rank(self, i, j):
# Find the representatives (or the root nodes) for the set that includes i and j
irep = self.find(i)
jrep = self.find(j)
# Elements are in the same set, no need to unite anything
if irep == jrep:
return
# Get the rank of i's tree
irank = self.rank[irep]
# Get the rank of j's tree
jrank = self.rank[jrep]
# If i's rank is less than j's rank
if irank < jrank:
# Move i under j
self.parent[irep] = jrep
# Else if j's rank is less than i's rank
elif jrank < irank:
# Move j under i
self.parent[jrep] = irep
# Else if their ranks are the same
else:
# Move i under j (doesn't matter which one goes where)
self.parent[irep] = jrep
# Increment the result tree's rank by 1
self.rank[jrep] += 1
def main(self):
# Example usage
size = 5
ds = DisjointSet(size)
# Perform some union operations
ds.union_by_rank(0, 1)
ds.union_by_rank(2, 3)
ds.union_by_rank(1, 3)
# Find the representative of each element
for i in range(size):
print(f"Element {i} belongs to the set with representative {ds.find(i)}")
# Creating an instance and calling the main method
ds = DisjointSet(size=5)
ds.main()
按大小合并:
同样,我们需要一个新的整数数组,名为size[] 。此数组的大小与父数组Parent[]相同。如果 i 代表一个集合,则size[i]是代表该集合的树中元素的数量。 现在我们将两棵树(或集合)合并起来,我们将它们称为左树和右树,在这种情况下,一切都取决于左树(或集合)的大小和右树(或集合)的大小。
1、如果左边的尺寸小于右边的尺寸,那么最好将左边移到右边下方,并将右边的尺寸增加左边的尺寸。同样,如果右边的尺寸小于左边的尺寸,那么我们应该将右边移到左边下方,并将左边的尺寸增加右边的尺寸。
2、如果尺寸相等,那么哪棵树位于另一棵树下都没有关系。
# Python program for the above approach
class UnionFind:
def __init__(self, n):
# Initialize Parent array
self.Parent = list(range(n))
# Initialize Size array with 1s
self.Size = [1] * n
# Function to find the representative (or the root node) for the set that includes i
def find(self, i):
if self.Parent[i] != i:
# Path compression: Make the parent of i the root of the set
self.Parent[i] = self.find(self.Parent[i])
return self.Parent[i]
# Unites the set that includes i and the set that includes j by size
def unionBySize(self, i, j):
# Find the representatives (or the root nodes) for the set that includes i
irep = self.find(i)
# And do the same for the set that includes j
jrep = self.find(j)
# Elements are in the same set, no need to unite anything.
if irep == jrep:
return
# Get the size of i’s tree
isize = self.Size[irep]
# Get the size of j’s tree
jsize = self.Size[jrep]
# If i’s size is less than j’s size
if isize < jsize:
# Then move i under j
self.Parent[irep] = jrep
# Increment j's size by i's size
self.Size[jrep] += self.Size[irep]
# Else if j’s size is less than i’s size
else:
# Then move j under i
self.Parent[jrep] = irep
# Increment i's size by j's size
self.Size[irep] += self.Size[jrep]
# Example usage
n = 5
unionFind = UnionFind(n)
# Perform union operations
unionFind.unionBySize(0, 1)
unionFind.unionBySize(2, 3)
unionFind.unionBySize(0, 4)
# Print the representative of each element after unions
for i in range(n):
print("Element {}: Representative = {}".format(i, unionFind.find(i)))
# This code is contributed by Susobhan Akhuli
输出
元素 0:代表 = 0
元素 1:代表 = 0
元素 2:代表 = 2
元素 3:代表 = 2
元素 4:代表 = 0
时间复杂度:O(log n),无路径压缩。
下面是具有路径压缩和按等级合并的不相交集的完整实现。
# Python3 program to implement Disjoint Set Data
# Structure.
class DisjSet:
def __init__(self, n):
# Constructor to create and
# initialize sets of n items
self.rank = [1] * n
self.parent = [i for i in range(n)]
# Finds set of given item x
def find(self, x):
# Finds the representative of the set
# that x is an element of
if (self.parent[x] != x):
# if x is not the parent of itself
# Then x is not the representative of
# its set,
self.parent[x] = self.find(self.parent[x])
# so we recursively call Find on its parent
# and move i's node directly under the
# representative of this set
return self.parent[x]
# Do union of two sets represented
# by x and y.
def Union(self, x, y):
# Find current sets of x and y
xset = self.find(x)
yset = self.find(y)
# If they are already in same set
if xset == yset:
return
# Put smaller ranked item under
# bigger ranked item if ranks are
# different
if self.rank[xset] < self.rank[yset]:
self.parent[xset] = yset
elif self.rank[xset] > self.rank[yset]:
self.parent[yset] = xset
# If ranks are same, then move y under
# x (doesn't matter which one goes where)
# and increment rank of x's tree
else:
self.parent[yset] = xset
self.rank[xset] = self.rank[xset] + 1
# Driver code
obj = DisjSet(5)
obj.Union(0, 2)
obj.Union(4, 2)
obj.Union(3, 1)
if obj.find(4) == obj.find(0):
print('Yes')
else:
print('No')
if obj.find(1) == obj.find(0):
print('Yes')
else:
print('No')
# This code is contributed by ng24_7.
输出
Yes
No
时间复杂度:创建 n 个单项集的时间为 O(n)。两种技术(路径压缩和按等级/大小合并)的时间复杂度将达到接近常数时间。事实证明,最终的 摊销时间复杂度为 O(α(n)),其中 α(n) 是逆阿克曼函数,其增长非常稳定(当 n<10 600 ![]() 时,它甚至不会超过)。
时,它甚至不会超过)。
空间复杂度: O(n),因为我们需要在不相交集数据结构中存储 n 个元素。
相关文章:
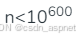
python 不相交集简介(并查集算法)【Introduction to Disjoint Set (Union-Find Algorithm)】
什么是不相交集数据结构? 如果两个集合没有任何共同元素,则它们被称为不相交集,集合的交集为空集。 存储不重叠或不相交元素子集的数据结构称为不相交集合数据结构。不相交集合数据结构支持以下操作: 1、将新集合添加到不相交集合…...
23种设计模式之工厂方法模式
文章目录 1. 简介2. 代码2.1 抽象类:Course.java2.2 产品A:JavaCourse.java2.3 产品B:PythonCourse.java2.4 工厂抽象类:CourseFactory.java2.5 产品A的工厂A:JavaCourseFactory.java2.6 产品B的工厂B:PyCo…...
Redis——事务
文章目录 Redis 事务Redis 的事务和 MySQL 事务的区别:事务操作MULTIEXECDISCARDWATCHUNWATCHwatch的实现原理 总结 Redis 事务 什么是事务 Redis 的事务和 MySQL 的事务 概念上是类似的. 都是把⼀系列操作绑定成⼀组. 让这⼀组能够批量执行 Redis 的事务和 MySQL 事务的区别:…...

Redis非关系型数据库操作命令大全
以下是 Redis 的常用操作命令大全,涵盖了键值操作、字符串、哈希、列表、集合、有序集合、发布/订阅、事务等多个方面的操作。 1. 通用键命令 命令说明SET key value设置指定 key 的值GET key获取指定 key 的值DEL key删除指定的 keyEXISTS key检查 key 是否存在E…...

基于SpringBoot+Vue+uniapp微信小程序的澡堂预订的微信小程序的详细设计和实现
项目运行截图 技术框架 后端采用SpringBoot框架 Spring Boot 是一个用于快速开发基于 Spring 框架的应用程序的开源框架。它采用约定大于配置的理念,提供了一套默认的配置,让开发者可以更专注于业务逻辑而不是配置文件。Spring Boot 通过自动化配置和约…...
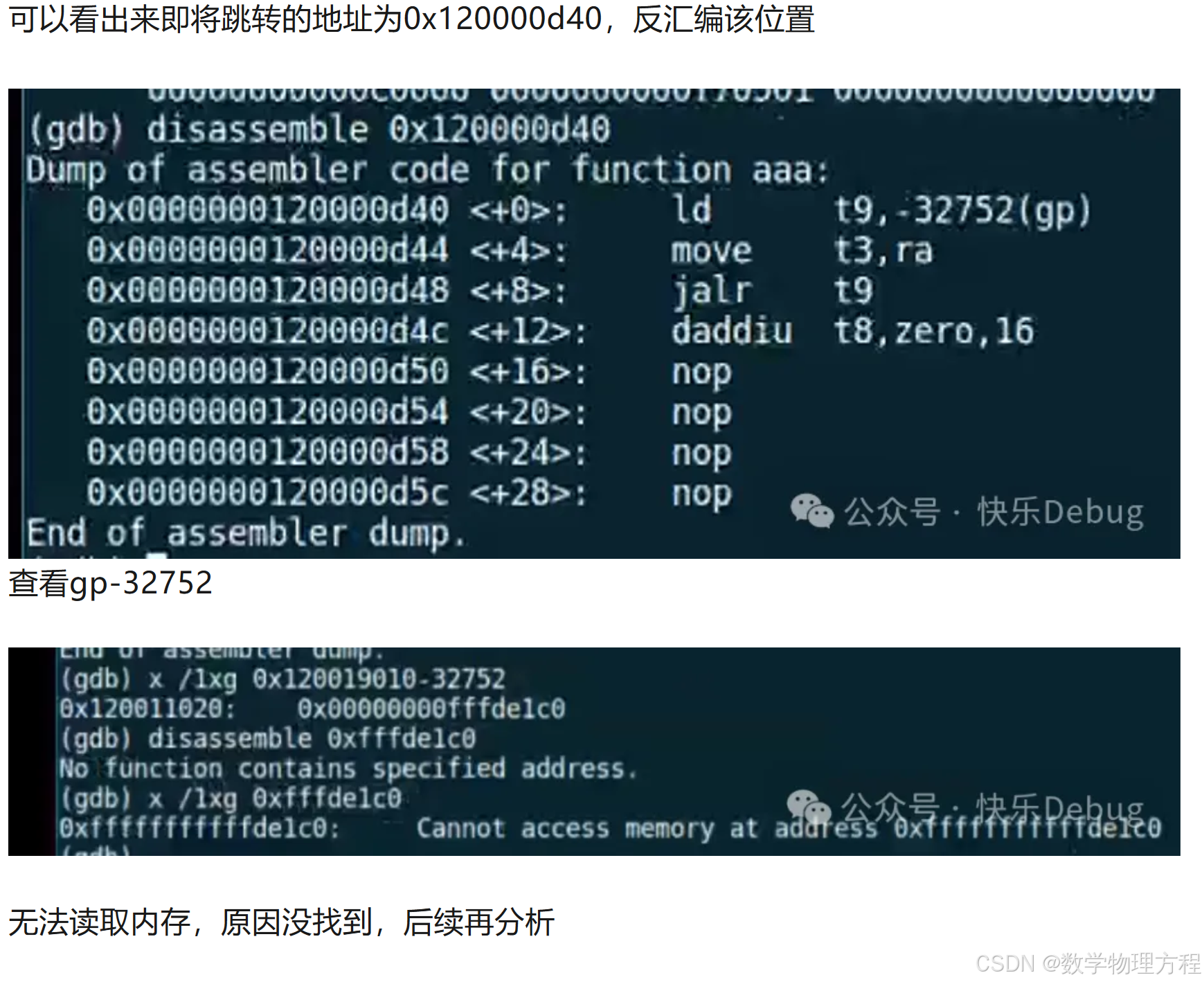
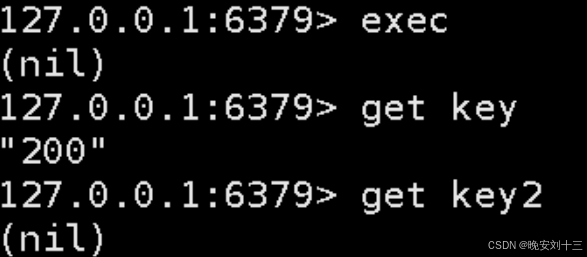
Linux mips架构链接库函数调用plt表汇编代码分析
linux调用共享库中的函数时通过plt表和got表实现位置无关代码,过程中涉及到lazy binding,即在第一调用外部函数时解析被调用的函数地址并将地址写入到got表,后续调用则不需要解析函数地址。这一部分和硬件架构有关,具体的是和cpu指…...
python 作业1
任务1: python为主的工作是很少的 学习的python的优势在于制作工具,制作合适的工具可以提高我们在工作中的工作效率的工具 提高我们的竞争优势。 任务2: 不换行 换行 任务3: 安装pycharm 进入相应网站Download PyCharm: The Python IDE for data science and we…...

Apache 出现 “403 forbidden“ 排查方法
1、检查运行 Apache 进程的用户没有对目录具备读取权限 如果该用户没有对 Directory 指定的目录具备适当的读取权限,就会导致 403 错误。 例如:使用用户apache启动Apache进程,但是apache用户对 Directory 指定的目录没有读取权限 2、检查…...

vue video播放m3u8监控视频
很关键的问题 vite创建的项目不需要import ‘videojs-contrib-hls’ 导入就报错 直接添加如下代码即可 html5: {vhs: {overrideNative: true},nativeVideoTracks: false,nativeAudioTracks: false,nativeTextTracks: false} 下面是完整组件示例 <template><div>…...
uniapp 获取签名证书 SHA1 自有证书签名打包
1.登录你的Dcloud 账户 2.找到我的应用菜单 3.点开某个应用 4.查看证书详情,里面有SHA1 和别名,密码,下载证书用于云打包,可以选择自有证书,输入别名,密码打包...
)
Open3d开发点云标注工具问题总结(二)
前面我们介绍了使用AABB方式来框选点云,但这种方式还是不够直观,我们的构想是设计一个和o3d.visualization.VisualizerWithEditing的点云框选方法一样的软件,因此,博主想到利用投影的形式进行解决: 具体的,…...
【FreeRTOS】
报错: 使用STM32cubemx自动生成freertos选项V2报错,V1不报错 …/Middlewares/Third_Party/FreeRTOS/Source/CMSIS_RTOS_V2/freertos_os2.h(31): 解决 修改cubemx配置,将V1.8.6改选为V1.8.5后编译不再报错...

洛谷 P4995:跳跳! ← 贪心算法
【题目来源】https://www.luogu.com.cn/problem/P4995【题目描述】你是一只小跳蛙,你特别擅长在各种地方跳来跳去。 这一天,你和朋友小 F 一起出去玩耍的时候,遇到了一堆高矮不同的石头,其中第 i 块的石头高度为 hi,地…...

代理 IP 在 AI 爬虫中的关键应用
现如今,人工智能(AI)的发展日新月异,而数据作为驱动 AI 发展的关键要素,其重要性不言而喻。AI 爬虫作为获取大量数据的重要工具,在数据收集过程中发挥着至关重要的作用。而代理 IP 在 AI 爬虫中有着广泛而重…...

【Vercel】Vercel静态部署踩坑
背景 在现代的软件开发中,自动化部署是一个不可或缺的环节。Vercel作为一个流行的前端部署平台,提供了与GitHub的无缝集成,使得开发者能够在每次提交代码后自动触发部署流程。然而,自动化部署过程中可能会遇到一些挑战࿰…...

【Spring】关于Spring中aware相关接口的作用
Aware 接口的回调方法是在 Bean 实例化之后调用的。具体来说,这些回调方法是在依赖注入完成后,但在 Bean 完全初始化之前调用的。这是 Spring 容器管理 Bean 生命周期的一部分 完成了属性赋值之后,Spring会执行一些回调,包括&…...

动态内存管理及RAII的简单应用
目录 一.程序启动所关联的内存分区 二.动态内存的申请和释放 三.将RAII思想融入代码 四.RAII思想的简单应用 一.程序启动所关联的内存分区 .dll文件是Dynamic Link Library(动态链接库)文件的缩写,它是一种共享库文件,包含…...
7、Vue2(一)
1.认识Vue 官网地址:https://v2.cn.vuejs.org/v2/guide/ Vue.js 是一套构建用户界面的渐进式框架。 Vue 2 是在2016年发布使用,2020是 vue3 才刚发布,时隔一年左右就已经将 vue3 作为了默认版本 尤雨溪,Vue.js和Vite的作者&…...

Chapter11
11.3 #include <stdio.h> #include <string.h> #define NUM_STUDENTS 40 #define NUM_SUBJECTS 3 // 学生结构体 typedef struct { int id; char name[50]; float scores[NUM_SUBJECTS]; float average; } Student; void inputData(Student studen…...
-----预训练)
LLAMA2入门(一)-----预训练
Llama 2 是预训练和微调的LLM系列,Llama 2 和 Llama 2-Chat 模型的参数规模达到 70B。Llama 2-Chat 模型专门为对话场景进行了优化。 这是一个系列的文章,会分别从LLAMA2的预训练,微调,安全性等方面进行讲解。 1.数据来源 数据…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...
