BF 算法
目录
BF算法
算法思路
完整代码
时间复杂度
查找所有起始位置
BF算法
BF算法:即暴力(Brute Force)算法,是一种模式匹配算法,将目标串 S 的第一个字符与模式串 T 的第一个字符进行匹配,若相等,则继续比较 S 的第二个字符和 T 的第二个字符;若不相等,则比较 S 的第二个字符和 T 的第一个字符,依次比较下去,直到得出最后的匹配结果
例如:
给定字符串S :"abcdef" 作为主串,给定字符串T: "cd" 作为子串,此时,就需要在主串中查找是否出现子串,若出现,则返回主串中第一个匹配字符的下标;若未出现,则返回 -1
接下来,我们就来看 BF 算法是如何在主串中查找子串的,也就是 BF 算法的思路
算法思路
我们通过一个具体的例子来看:

定义 i 指向主串的 0 下标,j 指向子串的 0 下标
以主串的 0 下标位置作为起始位置开始匹配:

判断 i 位置的字符是否和 j 位置的字符相等, i 位置和 j 位置字符都为 a,相等,则这两个字符匹配成功,i 和 j 向后移动,继续匹配

继续判断 i 位置字符 是否与 j 位置字符相等, i 位置和 j 位置字符都为 b,相等,这两个字符也匹配成功,i 和 j 继续向后移动,进行匹配

继续判断 i 位置字符 是否与 j 位置字符相等,i 位置字符为 c,j 位置字符为 e,不相等,说明以 a(0 下标位置) 为起始位置匹配子串匹配失败
此时,需要将 i 进行回退,由于 a(0下标)作为起始位置匹配失败,因此,继续以 b (1下标)作为起始位置开始尝试匹配,也就是以 原起始位置 + 1 作为新的起始位置开始重新匹配
同样,j 也需要回退,需要将 j 回退到 0 下标位置,与下一个起始位置重新开始匹配

由于 i 向前移动,当匹配失败时,我们该如何确定起始位置呢?
由于当 i 和 j 匹配成功时,两者会同时向后移动,因此,通过 j 就可以知道 i 向前移动了多少步
i - j 就是本次匹配的起始位置,而 i - j + 1 也就是新的起始位置
以 1 下标为起始位置继续匹配:

i 位置字符为 b,j 位置字符为 a,不相等,说明以 b 为起始位置匹配子串匹配失败,再次回退,由于 i = 1,j = 0,因此,新的起始位置为 2,j 的位置为 0

继续匹配, i 位置字符为 c,j 位置字符为 a,不相等,说明以 c 为起始位置匹配子串匹配失败,再次回退,由于 i = 2,j = 0,因此,新的起始位置为 3,j 的位置为 0

继续匹配, i 位置和 j 位置字符都为 a,相等,这两个字符匹配成功,i 和 j 向后移动

继续匹配, i 位置和 j 位置字符都为 b,相等,这两个字符也匹配成功,i 和 j 向后移动

继续匹配, i 位置和 j 位置字符都为 e,相等,这两个字符也匹配成功,i 和 j 向后移动

此时,子串已经遍历完了,也就说明 子串 中的所有字符都与 主串 中的字符相匹配,在主串中找到了子串,此时,就可以直接返回主串中本次匹配的起始位置,也就是 i - j
而若是主串先遍历完成,也就说明 主串 中没有与 子串 中字符完全匹配的字符串,找不到,此时,就需要返回 -1
总结一下上述过程:
1. 定义 i 指向主串的 0 下标,j 指向子串的 0 下标
2. 判断 i 位置字符与 j 位置字符是否相同,若相同,i 和 j 同时向后移动(i++ 且 j++);若不同,则i 和 j 都需要进行回退(i = i - j + 1,j = 0)
3. 重复 2 过程,直到遍历完 主串 或 子串,若子串先遍历完,说明在主串中找到了子串,匹配成功,返回起始位置(i - j);若主串先遍历完,说明主串中找不到子串,匹配失败,返回 -1
在分析了 BF 算法的思路之后,我们就来尝试编写代码
完整代码
/*** 判断主串中是否含有子串* @param str 主串* @param target 子串* @return 主串中含有子串,返回主串中子串第一次出现的起始下标;若不含有,返回 -1*/public int BF(String str, String target) {// 处理特殊情况if (str == null || target == null) {return -1;}int strLen = str.length();int targetLen = target.length();if (strLen == 0 || strLen < targetLen) {return -1;}// 开始判断int i = 0, j = 0;while (i < strLen && j < targetLen) {// 判断 str 中 i 位置字符是否与 target 中j 位置字符相同if (str.charAt(i) == target.charAt(j)) {// 相同,i 和 j 都向后移动i++;j++;} else {// 不相同,i 和 j 都进行回退i = i - j + 1;j = 0;}}// 子串先遍历完if (j >= targetLen) {return i - j;} else {// 主串先遍历完return -1;}}接下来,我们来分析 BF 算法的时间复杂度
时间复杂度
假设主串长度为 M,子串长度为 N
在最坏情况下,
在主串的前 M - N 个位置,每一次匹配时,都要比较到子串的最后一个字符(比较 N 次),才发现匹配不成功,然后再将 i 和 j 退回,继续比较,一共比较了 (M - N) * N
在 主串的最后 N 个位置,也分别匹配了 N、N - 1、N - 2...次,也就是 (N + 1)(N) / 2
因此,时间复杂度为 O(M*N)
上述我们查找的是主串中子串第一次出现时的起始位置,那么, 若我们想要查找主串中与子串相同的字符串的所有起始位置,该如何实现呢?
查找所有起始位置
与查找 主串中子串第一次出现的起始位置 思路相同
但是,当我们找到第一个起始位置(也就是 j 第一次遍历完子串时)时,不能直接返回,而是要继续在主串中查找
例如:

j 第一次遍历完子串:

以 0 下标为起始的字符串与子串匹配成功,将 0 下标存储起来,然后继续查找
此时,以 i + 1 为起始位置的字符串可能与字符相同,因此需要将 i 进行回退,继续查找
同时,也需要将 j 回退到 0 下标位置,重新开始匹配

总结一下上述过程:
1. 定义 i 指向主串的 0 下标,j 指向子串的 0 下标
2. 判断 i 位置字符与 j 位置字符是否相同,若相同,i 和 j 同时向后移动(i++ 且 j++);若不同,则i 和 j 都需要进行回退(i = i - j + 1,j = 0)
3. 判断 j 是否遍历完子串,若遍历完,则存储起始位置(i - j),再将 i 和 j 进行回退(i = i - j + 1,j = 0)
4. 重复 2、3 直到主串遍历完成
代码实现:
/*** 查找主串中与子串相同的字符串的所有起始位置* @param str 主串* @param target 子串* @return 查询结果集*/public List<Integer> BF(String str, String target) {List<Integer> ret = new ArrayList<>();// 处理特殊情况if (str == null || target == null) {return ret;}int strLen = str.length();int targetLen = target.length();if (strLen == 0 || strLen < targetLen) {return ret;}// 开始判断int i = 0, j = 0;while (i < strLen) {// 判断 str 中 i 位置字符是否与 target 中j 位置字符相同if (str.charAt(i) == target.charAt(j)) {// 相同,i 和 j 都向后移动i++;j++;} else {// 不相同,i 和 j 都进行回退i = i - j + 1;j = 0;}// 判断子串是否遍历完成if (j >= targetLen) {ret.add(i - j);i = i - j + 1;j = 0;}}return ret;}相关文章:

BF 算法
目录 BF算法 算法思路 完整代码 时间复杂度 查找所有起始位置 BF算法 BF算法:即暴力(Brute Force)算法,是一种模式匹配算法,将目标串 S 的第一个字符与模式串 T 的第一个字符进行匹配,若相等,则继续比较 S 的第二…...

SHOW-O——一款结合多模态理解和生成的单一Transformer
1.前言 大型语言模型 (LLM) 的重大进步激发了多模态大型语言模型 (MLLM) 的发展。早期的 MLLM 工作,例如 LLaVA、MiniGPT-4 和 InstructBLIP,展示了卓越的多模态理解能力。为了将 LLM 集成到多模态领域,这些研究探索了将预训练的模态特定编码…...

缓存框架JetCache源码解析-缓存变更通知机制
为什么需要缓存变更通知机制?如果我们使用的是本地缓存或者多级缓存(本地缓存远程缓存),当其中一个节点的本地缓存变更之后,为了保证缓存尽量的一致性,此时其他节点的本地缓存也需要去变更,这时…...

Android 设置特定Activity内容顶部显示在状态栏底部,也就是状态栏的下层 以及封装一个方法修改状态栏颜色
推荐:https://github.com/gyf-dev/ImmersionBar 在 Android 中要实现特定 Activity 内容顶部显示在状态栏底部以及封装方法修改状态栏颜色,可以通过以下步骤来完成: 一、让 Activity 内容显示在状态栏底部 在 AndroidManifest.xml 文件中,为特…...
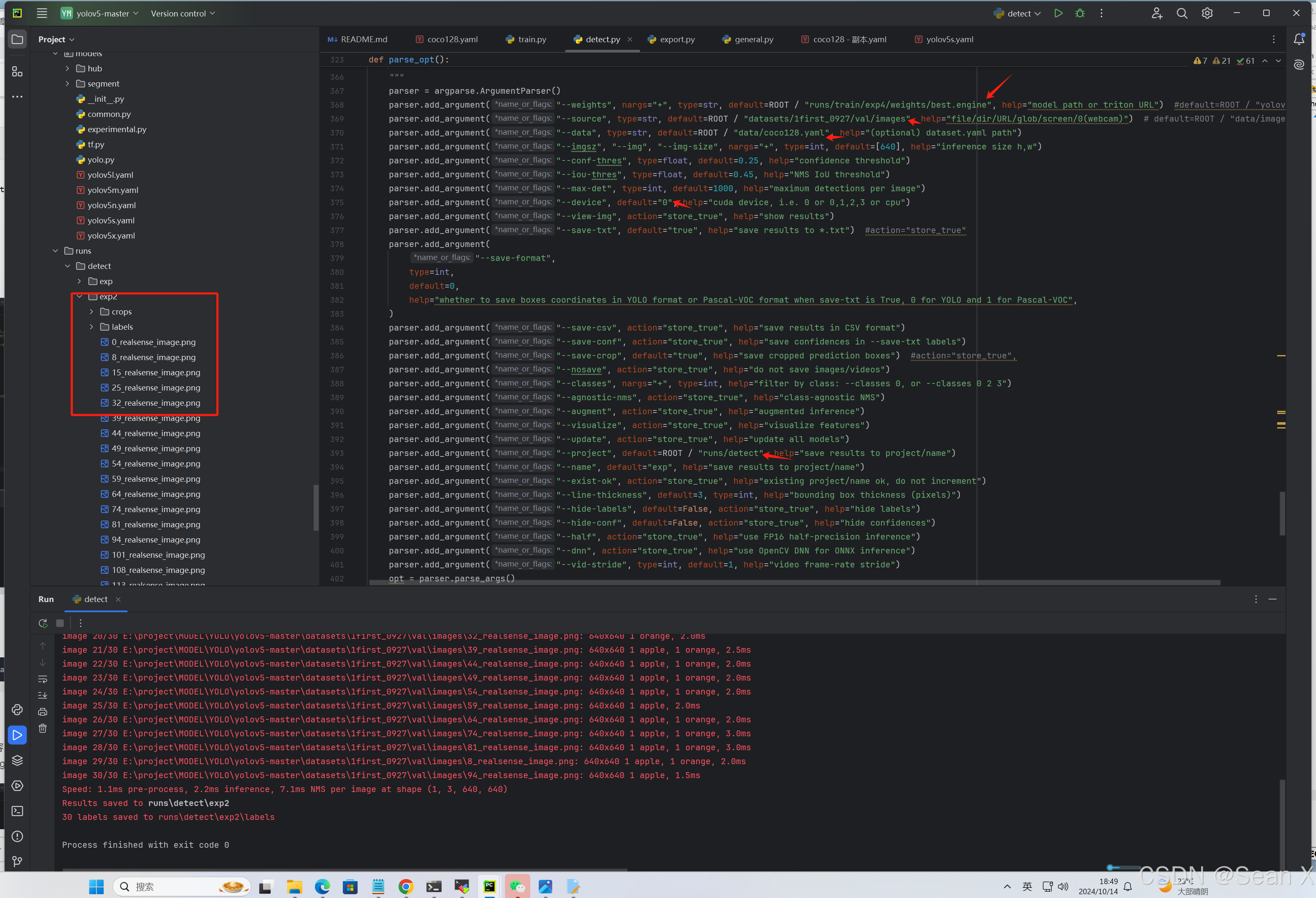
用自己的数据集复现YOLOv5
yolov5已经出了很多版本了,这里我以目前最新的版本为例,先在官网下载源码:GitHub - ultralytics/yolov5: YOLOv5 🚀 in PyTorch > ONNX > CoreML > TFLite 然后下载预训练模型,需要哪个就点击哪个模型就行&am…...

如何在博客中插入其他的博客链接(超简单)最新版
如何在博客中插入其他的博客链接 1.复制自己要添加的网址(组合键:Ctrlc)2. 点击超链接按钮3. 粘贴自己刚才复制的网址(组合键:Ctrlv)并点击确定即可4.让博客链接显示中文5.点击蓝字即可打开 1.复制自己要添…...

JS通过递归函数来剔除树结构特定节点
最近在处理权限类问题过程中,遇到多次需要过滤一下来列表的数据,针对不同用户看到的数据不同。记录一下 我的数据大致是这样的: class UserTree {constructor() {this.userTreeData [// 示例数据{ nodeid: "1", nodename: "R…...

javayufa
1.变量、运算符、表达式、输入输出 编写一个简单的Java程序–手速练习 public class Main { public static void main(String[] args) { System.out.println("Hello World"); } } 三、语法基础 变量 变量必须先定义,才可以使用。不能重名。 变量定义的方…...

软考-高级系统分析师知识点-补充篇
云计算 云计算的体系结构由5部分组成,分别为应用层,平台层,资源层,用户访问层和管理层,云计算的本质是通过网络提供服务,所以其体系结构以服务为核心。 系统的可靠性技术---容错技术---冗余技术 容错是指系…...

JavaScript全面指南(四)
🌈个人主页:前端青山 🔥系列专栏:JavaScript篇 🔖人终将被年少不可得之物困其一生 依旧青山,本期给大家带来JavaScript篇专栏内容:JavaScript全面指南 目录 61、如何防止XSRF攻击 62、如何判断一个对象是否为数组&…...

2024年诺贝尔物理学奖的创新之举
对于2024年诺贝尔物理学奖的这一创新之举,我的观点可以从以下几点展开: 跨学科融合的里程碑:将诺贝尔物理学奖颁发给机器学习与神经网络领域的研究者,标志着科学界对跨学科合作和融合的认可达到新高度。这不仅体现了理论物理与计算…...

FileLink内外网文件交换——致力企业高效安全文件共享
随着数字化转型的推进,企业之间的文件交流需求日益增加。然而,传统的文件传输方式往往无法满足速度和安全性的双重要求。FileLink作为一款专注于跨网文件交换的工具,致力于为企业提供高效、安全的文件共享解决方案。 应用场景一:项…...

使用Python在Jupyter Notebook中显示Markdown文本
使用Python在Jupyter Notebook中显示Markdown文本 引言1. 导入必要的模块2. 定义一个函数来显示Markdown文本3. 使用print_md函数显示Markdown文本4. 总结 引言 作为一名Python初级程序员,你可能已经熟悉了Jupyter Notebook这个强大的工具。Jupyter Notebook不仅支…...

G1 GAN生成MNIST手写数字图像
🍨 本文为🔗365天深度学习训练营 中的学习记录博客🍖 原作者:K同学啊 G1 GAN生成MNIST手写数字图像 1. 生成对抗网络 (GAN) 简介 生成对抗网络 (GAN) 是一种通过“对抗性”学习生成数据的深度学习模型,通常用于生成…...

WPFDeveloper正式版发布
WPFDeveloper WPFDeveloper一个基于WPF自定义高级控件的WPF开发人员UI库,它提供了众多的自定义控件。 该项目的创建者和主要维护者是现役微软MVP 闫驚鏵: https://github.com/yanjinhuagood 该项目还有众多的维护者,详情可以访问github上的README&…...
)
实现鼠标经过某个元素时弹出提示框(通常称为“工具提示”或“悬浮提示”)
要实现鼠标经过某个元素时弹出提示框(通常称为“工具提示”或“悬浮提示”),你可以使用 JavaScript 结合 CSS 来创建这个效果。以下是详细步骤,包括 HTML、CSS 和 JavaScript 的代码示例。 HTML 结构 首先,创建一个简…...

【GAMES101笔记速查——Lecture 17 Materials and Appearances】
目录 1 材质和外观 1.1 自然界中,外观是光线和材质共同作用的结果 1.2 图形学中,什么是材质? 1.2.1 渲染方程严格正确,其中BRDF项决定了物体的材质 1.2.2 漫反射材质 (1)如何定义漫反射系数࿱…...

对于从vscode ssh到virtualBox的timeout记录
如题,解决方式如下: 1.把虚拟机关机退出来,在这个界面进行网络设置:选桥接网卡 2.然后再进系统,使用命令 ip addr查看如今的ip地址,应该和在本机里面看到的是一个网段 3.打开vscode,该干啥干…...

鸿蒙原生应用扬帆起航
就在2024年6月21日华为在开发者大会上发布了全新操作的系统HarmonyOS Next开发测试版,网友们把它称之为“称之为纯血鸿蒙”。因为在此之前鸿蒙系统底层式有两套基础架构的,一套是是Android的AOSP,一套是鸿蒙的Open Harmony,因为早…...

《计算机视觉》—— 表情识别
根据计算眼睛、嘴巴的变化,判断是什么表情结合以下两篇文章来理解表情识别的实现方法 基于 dilib 库的人脸检测 https://blog.csdn.net/weixin_73504499/article/details/142977202?spm1001.2014.3001.5501 基于 dlib 库的人脸关键点定位 https://blog.csdn.net/we…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...
