「图::连通」详解并查集并实现对应的功能 / 手撕数据结构(C++)
目录
概述
成员变量
创建销毁
根节点访问
路径压缩
启发式合并
复杂度
Code
概述
并查集,故名思议,能合并、能查询的集合,在图的连通性问题和许多算法优化上着广泛的使用。
这是一个什么数据结构呢?
一般来讲,并查集是由一系列集合组成的集合群。
其中,每个集合都有一个根节点,它的父亲仍是它自己,集合内其余的节点的父亲or祖宗均是这个节点,这样,一个根节点就领导了一个集合。而并查集支持这样的多个集合的访问以及合并操作。

每个集合都是一个树形结构,你可以认为并查集是一片森林。
听起来挺复杂度,但是其实很好实现。
成员变量
static constexpr int N = 1e5 + 5;一个无关紧要的常量,限制最大值。
int pre[N];父节点指针数组,pre[i]=j表示i的父亲是j,即二者处于同一集合。
int size[N];集合大小数组,只用每个集合的根节点上的size是有意义的,若i为根节点size[i]=x表示i所在的集合大小为x。
struct union_find_set {static constexpr int N = 1e5 + 5;int pre[N],size[N];...
};创建销毁
在一开始,每个节点都单独成为一个集合,每个集合大小为1。
union_find_set(int n = N) {for (int i = 0; i < n; i++) {pre[i] = i;size[i] = 1;}
}根节点访问
给定一个节点x,我们想访问他的根节点。
这一步可以递归实现:我们知道只有根节点的pre指向自己,所以如果pre[x]==x,我们就找到了根节点,否则沿着pre指针爬,传入下一级root。
int root(int x) {return pre[x] == x ? x : root(pre[x]);
}路径压缩
沿着pre指针爬树的过程的时间复杂度是线性级别的,但是我们可以使用路径压缩:
当我们依次跳出递归时,额外将这一级x的pre指针更新为找到的根节点,这样,一棵树就由多层被压缩成了两层(根节点与叶子节点)。
int root(int x) {return pre[x] = (pre[x] == x ? x : root(pre[x]));
}启发式合并
想合并两个集合,我们可以采用启发式合并,即按规模合并。
路径压缩并不是实时的,所以一般一个集合仍是多层的。在这种情况下,为了保持查询根节点的高效性,我们应该将小集合接在大集合之下(小集合中节点少,向上访问的总代价小,如果反过来,那么大集合中的大量节点想向上访问会极其不利)。
给出两个节点,将其所在的集合合并,我们先找出root,如果两个节点确实属于不同集合,我们将小集合接在大集合之下,这样就能保持根节点查询的效率。最后根节点的size。
void unite(int x, int y) {x = root(x), y = root(y);if (x == y)return;if (size[y] < size[x])std::swap(x, y);pre[x] = y;size[y] += size[x];
}复杂度
时间复杂度:O(n) 使用路径压缩:O(1)~O(logn)
空间复杂度:O(n)
Code
#include <algorithm>
#ifndef UNION_FIND_SET
#define UNION_FIND_SET
struct union_find_set {static constexpr int N = 1e5 + 5;int pre[N],size[N];union_find_set(int n) {for (int i = 0; i < n; i++) {pre[i] = i;size[i] = 1;}}int root(int x) {return pre[x] = (pre[x] == x ? x : root(pre[x]));}int get_size(int x) {return size[root(x)];}void unite(int x, int y) {x = root(x), y = root(y);if (x == y)return;if (size[y] < size[x])std::swap(x, y);pre[x] = y;size[y] += size[x];}
};
#endif相关文章:

「图::连通」详解并查集并实现对应的功能 / 手撕数据结构(C++)
目录 概述 成员变量 创建销毁 根节点访问 路径压缩 启发式合并 复杂度 Code 概述 并查集,故名思议,能合并、能查询的集合,在图的连通性问题和许多算法优化上着广泛的使用。 这是一个什么数据结构呢? 一般来讲,并查集是…...

基于PSO粒子群优化的CNN-GRU-SAM网络时间序列回归预测算法matlab仿真
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 5.算法完整程序工程 1.算法运行效果图预览 (完整程序运行后无水印) PSO优化过程: PSO优化前后,模型训练对比: 数据预测对比: 误差回归对比&a…...

PyTorch 的 DataLoader 类介绍
DataLoader 类 功能与作用 PyTorch 是一个流行的开源机器学习库,它提供了一个名为 DataLoader 的类,用于加载数据集并将其封装成一个可迭代的对象。DataLoader 可以自动地将数据集划分为多个批次,并在训练过程中迭代地返回这些批次。是用于加…...

【设计模式系列】命令模式
目录 一、什么是命令模式 二、命令模式的角色 三、命令模式的典型应用场景 四、命令模式在Runnable中的应用 一、什么是命令模式 命令模式(Command Pattern)是一种行为设计模式,它将一个请求或简单操作封装为一个对象。这个模式提供了一种…...

uniapp中使用lottie实现JSON动画
uniapp中使用lottie实现JSON动画 不喜欢废话直接开干一、引入相关依赖二、在项目的目录新建目录结构三、操作步骤四、编写自定义组件代码五、组件的使用提一嘴更多lottie-web常用方法添加点击事件 不喜欢废话直接开干 一、引入相关依赖 npm install lottie-web # 如果有问题可…...
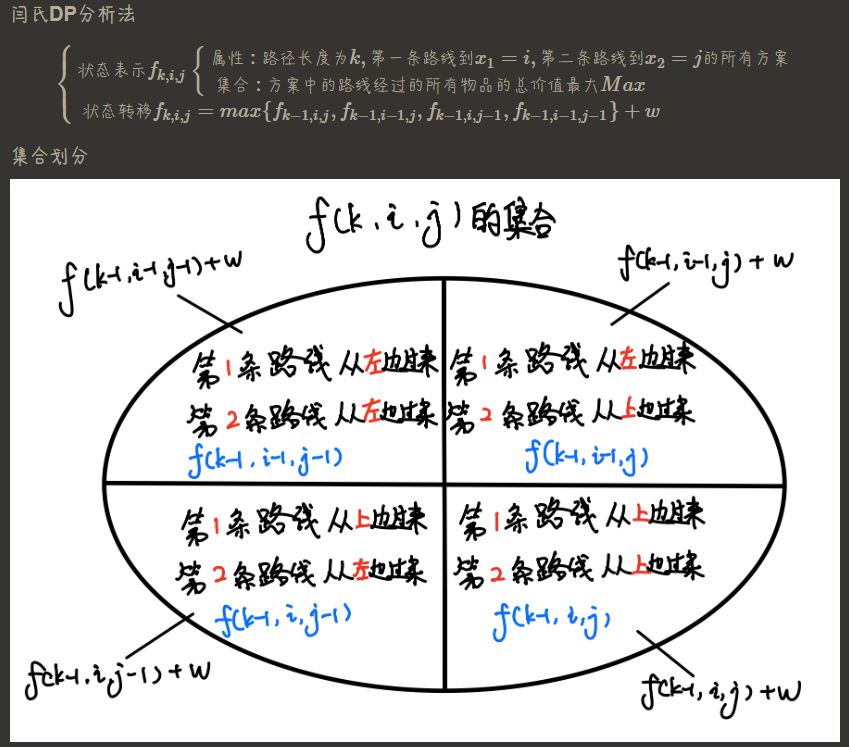
AcWing275
题目重述 这道题的核心是利用方格取数模型的思想,将两条路径的传递过程映射为同时出发的两条路径,避免重复格子的经过。题解通过以下步骤解题: 路径映射:从 (n, m) 回到 (1, 1) 的路径,可以转换成 (1, 1) 到 (n, m) …...

Windows系统部署redis自启动服务【亲测可用】
文章目录 引言I redis以本地服务运行(Windows service)使用MSI安装包配置文件,配置端口和密码II redis服务以终端命令启动缺点运行redis-server并指定端口和密码III 知识扩展确认redis-server可用性Installing the Service引言 服务器是Windows系统,所以使用Windows不是re…...

深入了解机器学习 (Descending into ML):线性回归
人们早就知晓,相比凉爽的天气,蟋蟀在较为炎热的天气里鸣叫更为频繁。数十年来,专业和业余昆虫学者已将每分钟的鸣叫声和温度方面的数据编入目录。Ruth 阿姨将她喜爱的蟋蟀数据库作为生日礼物送给您,并邀请您自己利用该数据库训练一…...

每日OJ题_牛客_集合_排序_C++_Java
目录 牛客_集合_排序 题目解析 C代码 Java代码 牛客_集合_排序 集合_牛客题霸_牛客网 (nowcoder.com) 题目解析 笔试题可直接用set排序,面试可询问是否要手写排序函数,如果要手写排序,推荐写快排。 C代码 #include <iostream> …...
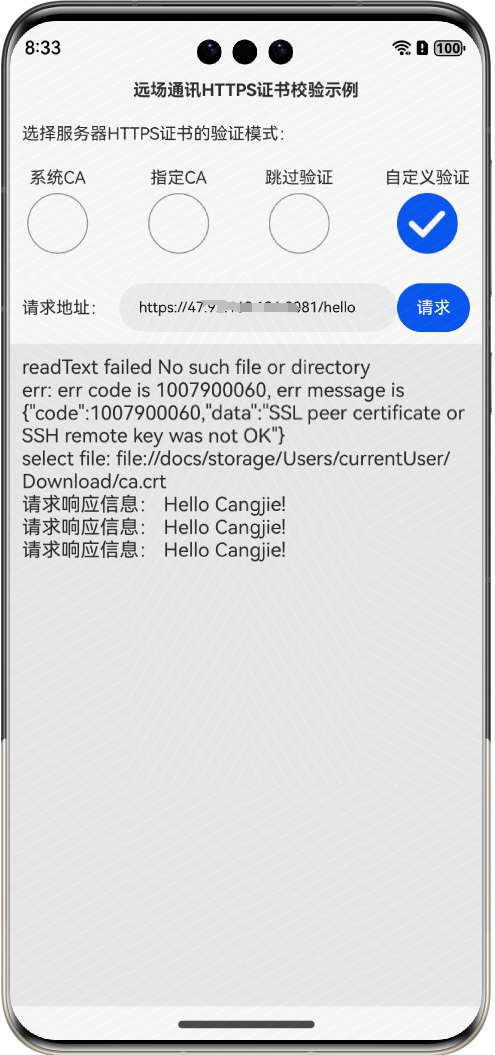
鸿蒙网络编程系列27-HTTPS服务端证书的四种校验方式示例
1. 服务端数字证书验证的问题 在鸿蒙客户端对服务端发起HTTPS请求时,如果使用HttpRequest的request发起请求,那么就存在服务端数字证书的验证问题,你只有两个选择,一个是使用系统的CA,一个是使用自己选定的CA…...

scala继承
Scala中继承的定义为在原有类的基础上定义一个新类,原有类称为父类,新类称为子类。 当子类从父类中继承的方法不能满足需要时,子类需要有自己的行为,怎么办? 此时使用override可以重写父类方法。 class Aniaml(){va…...

【Hive】2-Apache Hive概述、架构、组件、数据模型
Apache Hive概述 什么是Hive Apache Hive是一款建立在Hladoop之上的开源数据仓库系统,可以将存储在Hadoop文件中的结构化、半结构化数据文件映射为一张数据库表,基于表提供了一种类似SQL的查询模型,称为Hive查询语言(HQL),用于访…...

关于目前面试八股文的一些心得体会
现在是2024年10月,自22年开始,明显感觉到整个计算机行业,越来越卷了。一方面,随着信息的传播,越来越多的新人涌入了这个赛道,另一方面,众所周知的原因,不管大厂还是小厂在经历寒冬之…...

大数据-178 Elasticsearch Query - Java API 索引操作 文档操作
点一下关注吧!!!非常感谢!!持续更新!!! 目前已经更新到了: Hadoop(已更完)HDFS(已更完)MapReduce(已更完&am…...

PHP(一)从入门到放弃
参考文献:https://www.php.net/manual/zh/introduction.php PHP 是什么? PHP(“PHP: Hypertext Preprocessor”,超文本预处理器的字母缩写)是一种被广泛应用的开放源代码的多用途脚本语言,它可嵌入到 HTML…...

基于深度学习的生物启发的学习系统
基于深度学习的生物启发学习系统(Biologically Inspired Learning Systems)旨在借鉴生物大脑的结构和学习机制,设计出更高效、更灵活的人工智能系统。这类系统融合了生物神经科学的研究成果,通过模仿大脑中的学习模式、记忆过程和…...

10_实现readonly
在某些时候,我们希望定义一些数据是只读的,不允许被修改,从而实现对数据的保护,即为 readonly 只读本质上也是对数据对象的代理,我们同样可以基于之前实现的 createReactiveObject 函数来实现,可以为此函数…...

简单介绍$listeners
$listeners 它可以获取父组件传递过来的所有自定义函数,如下: // 父组件 <template><div class"a"><Child abab"handleAbab" acac"handleAcac"/></div> </template><script> impor…...

架构设计笔记-20-补充知识
知识产权 我国没有专门针对知识产权制定统一的法律(知识产权法),而是在民法通则规定的原则下,根据知识产权的不同类型制定了不同的单项法律及法规,如著作权法、商标法、专利法、计算机软件保护条例等,这些法律、法规共同构成了我…...

scrapy 爬虫学习之【中医药材】爬虫
本项目纯学习使用。 1 scrapy 代码 爬取逻辑非常简单,根据url来处理翻页,然后获取到详情页面的链接,再去爬取详情页面的内容即可,最终数据落地到excel中。 经测试,总计获取 11299条中医药材数据。 import pandas as…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...
