代码训练营 day39|0-1背包问题,LeetCode 416
前言
这里记录一下陈菜菜的刷题记录,主要应对25秋招、春招
个人背景
211CS本+CUHK计算机相关硕,一年车企软件开发经验
代码能力:有待提高
常用语言:C++
系列文章目录
第九章 动态规划part03
`
文章目录
- 前言
- 系列文章目录
- 第九章 动态规划part03
- 一、今日任务
- 二、详细布置
- 背包问题详解
- 二维数组版本
- dp数组定义
- dp递推公式
- dp数组初始化
- 确定遍历顺序
- 一维数组版本
- 确定dp数组的定义
- 一维dp数组的递推公式
- 一维dp数组遍历顺序
- 初始化
- 46. 携带研究材料
- 提示:
- 样例1:
- 思路
- 实战
- 一维数组求解法
- 416. 分割等和子集
- 提示:
- 样例1:
- 样例2:
- 思路
- 实战
- 总结
一、今日任务
● 01背包问题 二维
● 01背包问题 一维
● 416. 分割等和子集
二、详细布置
背包问题详解

完全背包又是也是01背包稍作变化而来,即:完全背包的物品数量是无限的
二维数组版本
dp数组定义
dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。(i 来表示物品、j表示背包容量)
dp递推公式
-不放物品i:背包容量为j,里面不放物品i的最大价值是dp[i - 1][j]。
-放物品i:背包空出物品i的容量后,背包容量为j - weight[i],dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]且不放物品i的最大价值,那么dp[i - 1][j - weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值
递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
dp数组初始化
首先从dp[i][j]的定义出发,如果背包容量j为0的话,即dp[i][0],无论是选取哪些物品,背包价值总和一定为0。
在看其他情况。
状态转移方程 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出i 是由 i-1 推导出来,那么i为0的时候就一定要初始化。
dp[0][j],即:i为0,存放编号0的物品的时候,各个容量的背包所能存放的最大价值。
那么很明显当 j < weight[0]的时候,dp[0][j] 应该是 0,因为背包容量比编号0的物品重量还小。
当j >= weight[0]时,dp[0][j] 应该是value[0],因为背包容量放足够放编号0物品。
for (int j = 0 ; j < weight[0]; j++) { // 当然这一步,如果把dp数组预先初始化为0了,这一步就可以省略,但很多同学应该没有想清楚这一点。dp[0][j] = 0;
}
// 正序遍历
for (int j = weight[0]; j <= bagweight; j++) {dp[0][j] = value[0];
}
最后初始化代码如下:
// 初始化 dp
vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));
for (int j = weight[0]; j <= bagweight; j++) {dp[0][j] = value[0];
}
确定遍历顺序
先遍历物品更好理解
// weight数组的大小 就是物品个数
for(int i = 1; i < weight.size(); i++) { // 遍历物品for(int j = 0; j <= bagweight; j++) { // 遍历背包容量if (j < weight[i]) dp[i][j] = dp[i - 1][j];else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);}
}
一维数组版本
确定dp数组的定义
dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j]
一维dp数组的递推公式
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
一维dp数组遍历顺序
for(int i = 0; i < weight.size(); i++) { // 遍历物品for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}
}
注意:这里和二维dp的写法中,遍历背包的顺序是不一样的!
二维dp遍历的时候,背包容量是从小到大,而一维dp遍历的时候,背包是从大到小。
倒序遍历是为了保证物品i只被放入一次!
代码中是先遍历物品嵌套遍历背包容量,那可不可以先遍历背包容量嵌套遍历物品呢?
不可以!
初始化
dp数组在推导的时候一定是取价值最大的数,如果题目给的价值都是正整数那么非0下标都初始化为0就可以了。
这样才能让dp数组在递归公式的过程中取的最大的价值,而不是被初始值覆盖了。
46. 携带研究材料
题目链接:卡码网46
文章讲解:代码随想录
小明是一位科学家,他需要参加一场重要的国际科学大会,以展示自己的最新研究成果。他需要带一些研究材料,但是他的行李箱空间有限。这些研究材料包括实验设备、文献资料和实验样本等等,它们各自占据不同的空间,并且具有不同的价值。
小明的行李空间为 N,问小明应该如何抉择,才能携带最大价值的研究材料,每种研究材料只能选择一次,并且只有选与不选两种选择,不能进行切割。
输入:
第一行包含两个正整数,第一个整数 M 代表研究材料的种类,第二个正整数 N,代表小明的行李空间。
第二行包含 M 个正整数,代表每种研究材料的所占空间。
第三行包含 M 个正整数,代表每种研究材料的价值。
输出:
输出一个整数,代表小明能够携带的研究材料的最大价值
提示:
数据范围:
1 <= N <= 5000
1 <= M <= 5000
研究材料占用空间和价值都小于等于 1000
样例1:
输入:
1 6 1
2 2 3 1 5 2
2 3 1 5 4 3
输出:
5
解释:
小明能够携带 6 种研究材料,但是行李空间只有 1,而占用空间为 1 的研究材料价值为 5,所以最终答案输出 5。
思路
这题就是0-1背包问题的经典应用。
实战
#include <bits/stdc++.h>
using namespace std;
int main(){int M,N;cin>>M>>N;vector<int> weight(M,0);vector<int> value(M,0);vector<vector<int>> dp(M,vector<int>(N+1,0));int i,j;for(i=0;i<M;i++){cin>>weight[i];}for(j=0;j<M;j++){cin>>value[j];}for(j=weight[0];j<=N;j++){dp[0][j]=value[0];}for(i=1;i<M;i++){for(j=0;j<=N;j++){if(j<weight[i])dp[i][j]=dp[i-1][j];elsedp[i][j]=max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]);}}cout<<dp[M-1][N]<<endl;return 0;
}一维数组求解法
#include <bits/stdc++.h>
using namespace std;
int main(){int n,bagweight;cin>>n>>bagweight;vector<int> weight(n,0);vector<int> value(n,0);int i,j;for(i=0;i<n;i++)cin>>weight[i];for(j=0;j<n;j++)cin>>value[j];vector<int> dp(bagweight+1,0);for(i=0;i<n;i++){for(j=bagweight;j>=weight[i];j--){dp[j]=max(dp[j],dp[j-weight[i]]+value[i]);}}cout<<dp[bagweight]<<endl;return 0;
}416. 分割等和子集
题目链接:LeetCode426
文章讲解:图文讲解
题目描述
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
提示:
1 <= nums.length <= 200
1 <= nums[i] <= 100
样例1:
输入:nums = [1,5,11,5]
输出:true
解释:数组可以分割成 [1, 5, 5] 和 [11]
样例2:
输入:nums = [1,2,3,5]
输出:false
解释:数组不能分割成两个元素和相等的子集。
思路
0-1背包的变形。
实战
class Solution {
public:bool canPartition(vector<int>& nums) {int sum=0;for(auto num:nums){sum+=num;}if(sum%2!=0)return false;int n=nums.size(),bagweight=sum/2;vector<int> dp(bagweight+1,0);int i,j;for(i=0;i<n;i++){for(j=bagweight;j>=nums[i];j--){dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);}}if(dp[bagweight]==bagweight)return true;return false;}
};
总结
今天主要学习了0-1背包问题,老师讲的很详细,理解起来不难。后面还需要多做题巩固一下代码。
加油,坚持打卡的第39天。
相关文章:

代码训练营 day39|0-1背包问题,LeetCode 416
前言 这里记录一下陈菜菜的刷题记录,主要应对25秋招、春招 个人背景 211CS本CUHK计算机相关硕,一年车企软件开发经验 代码能力:有待提高 常用语言:C 系列文章目录 第九章 动态规划part03 文章目录 前言系列文章目录第九章 动态…...

LeetCode 203 - 移除链表元素
题目描述 给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.val val 的节点,并返回 新的头节点 。 解题思路 创建一个虚拟头节点dummyHead,并将其next指向给定的头节点head,这样可以避免处理头节点的特…...

【海图界面上一些常见术语UTC、HDG、COG、SOG、LAT、LON的基本解释】
当然,以下是关于海图界面上一些常见术语UTC、HDG、COG、SOG、LAT、LON的基本解释: UTC (Coordinated Universal Time) 定义:UTC 是协调世界时(Coordinated Universal Time)的缩写,是一种与地球自转无关的…...

HL7协议简介及其在STM32上的解析实现
近期完成一个医疗相关的项目,其中包括了体征监测设备,该设备使用的通信协议便是HL7 V2.4 协议,在医疗信息化领域,HL7(Health Level Seven)协议扮演着至关重要的角色。它是一种国际标准,用于定义医疗机构间以及医疗设备与信息系统之间的数据交换格式和通信协议。HL7标准旨…...

TensorRT推理端到端
TensorRT推理端到端 1.参考链接2.宿主机上安装CUDA 12.4.13.安装nvidia-container-toolkit4.创建ghcr.io/intel/llvm/ubuntu2204_base容器5.容器内安装CUDA 12.4.1 + TensorRT10.1.06.安装依赖7.准备resnet50模型8.准备bert模型9.准备yolov5m模型10.编译TensorRT推理程序11.onn…...

获取历史的天气预报数据的网站
要获取从2019年到现在某个中国城市的天气数据,您可以通过以下方法实现: 1. 使用第三方天气数据API 许多天气服务提供商提供了历史天气数据的API接口,您可以通过这些API获取所需的数据。以下是一些常用的天气数据API提供商: 1.1…...

【VUE】Vue中常用的修饰符
事件修饰符 .stop:阻止事件冒泡。.prevent:阻止默认事件。.capture:使用事件捕获模式。.self:只当事件在该元素本身(比如不是子元素)触发时触发回调。.once:只触发一次事件。 按键修饰符 .en…...

数据分箱:如何确定分箱的最优数量?
选择最优分箱可以考虑以下几种方法: 一、基于业务理解 分析业务背景:从业务角度出发,某些特征可能有自然的分组或区间划分。例如,年龄可以根据不同的人生阶段进行分箱,收入可以根据常见的收入等级划分。 优点&#x…...

机器学习核心功能:分类、回归、聚类与降维
机器学习核心功能:分类、回归、聚类与降维 机器学习领域的基本功能类型通常按照学习模式、预测目标和算法适用性来分类。这些类型包括监督学习、无监督学习、半监督学习和强化学习,它们可以进一步细化为特定的任务,如分类、回归、聚类和降维…...

Python爬虫-eBay商品排名数据
前言 本文是该专栏的第39篇,后面会持续分享python爬虫干货知识,记得关注。 本文以eBay为例,通过搜索目标”关键词“,获取相关搜索”关键词“的商品排名数据。废话不多说,具体实现思路和详细逻辑,笔者将在正文结合完整代码进行详细介绍。接下来,跟着笔者直接往下看正文详…...
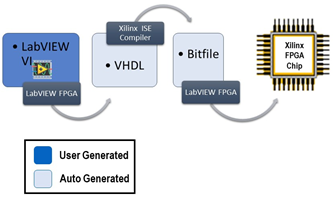
LabVIEW提高开发效率技巧----图像处理加速
在现代工业和科研中,图像处理技术被广泛应用于质量检测、自动化控制、机器人导航等领域。然而,随着图像数据量的增加,传统的CPU处理方式可能难以满足实时性和高效处理的需求。LabVIEW通过结合NI Vision模块和FPGA硬件平台,可以显著…...
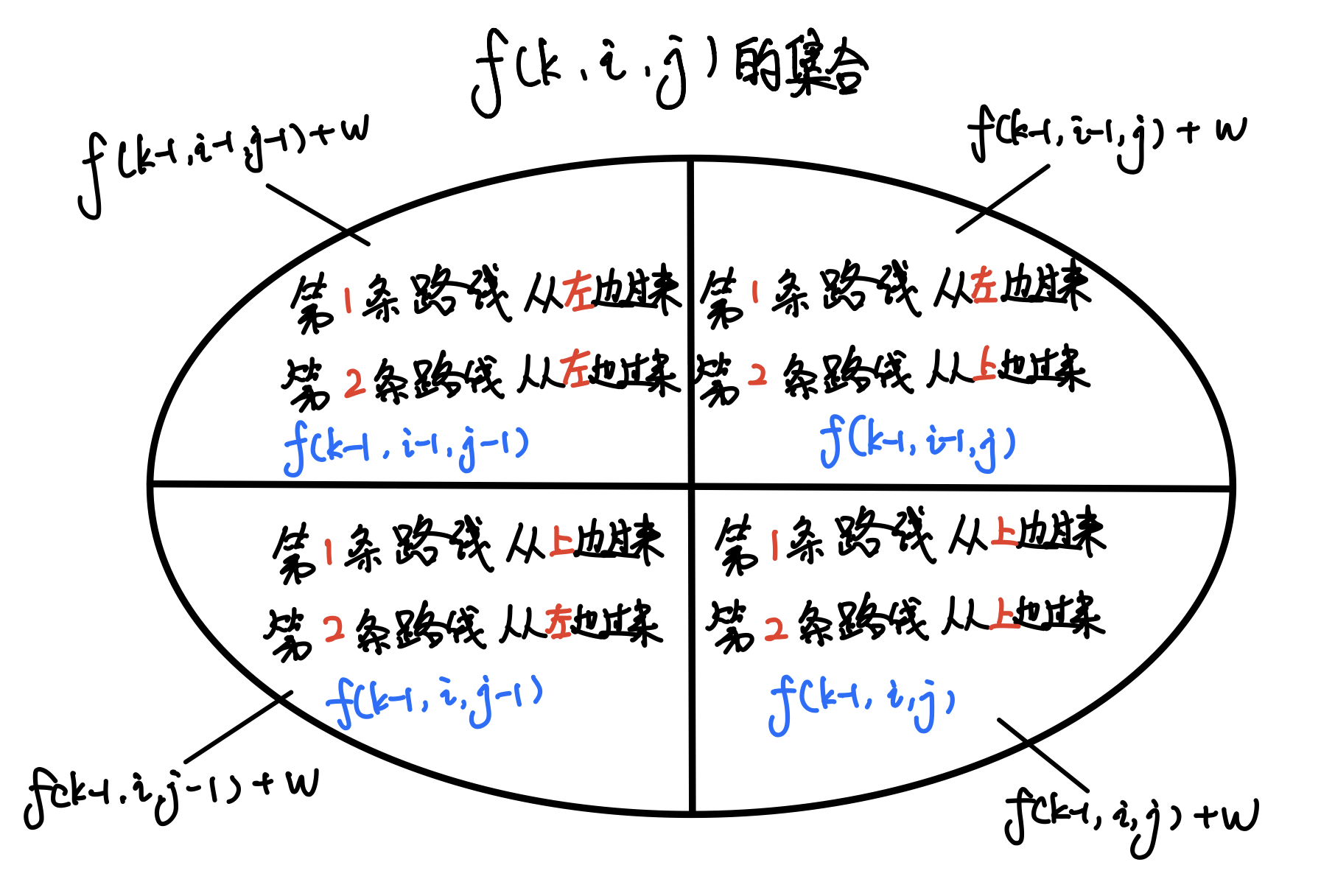
AcWing1027
题目重述: 题目的核心是找到一条路径的最大权值总和,但路径要从起点 (1, 1) 走到终点 (n, n)。由于两条路径分别经过不同的格子,我们可以巧妙地将问题简化为两次同时出发的路径问题。这种映射的设计让我们能够更方便地处理两条路径重叠在同一…...

23 Shell Script服务脚本
Linux 服务脚本 一、Linux 开机自动启动服务 linux开机服务原理: ①linux系统启动首先加载kernel ②初始操作系统 ③login验证程序等待用户登陆 初始化操作系统 kernel加载/sbin/init创建用户空间的第一个程序 该程序完成操作系统的初…...

三周精通FastAPI:3 查询参数
查询参数 FastAPI官网手册:https://fastapi.tiangolo.com/zh/tutorial/query-params/ 上节内容:https://skywalk.blog.csdn.net/article/details/143046422 声明的参数不是路径参数时,路径操作函数会把该参数自动解释为**查询**参数。 from…...

大语言模型学习指南:入门、应用与深入
0x00 学习路径概述 本文将学习路径划分为三个部分:入门篇、应用篇、深入篇。每个章节针对不同的学习需求,帮助你从基础知识入手,逐步掌握大语言模型(LLM)的使用、应用开发以及技术原理等内容。 学习目标 入门篇&…...

【Linux-进程间通信】匿名管道+4种情况+5种特征
匿名管道 匿名管道(Anonymous Pipes)是Unix和类Unix操作系统中的一种通信机制,用于在两个进程之间传递数据。匿名管道通常用于命令行工具之间的数据传递; 匿名管道的工作原理是创建一个临时文件,该文件被称为管道文件…...

Perl打印9x9乘法口诀
本章教程主要介绍如何用Perl打印9x9乘法口诀。 一、程序代码 1、写法① use strict; # 启用严格模式,帮助捕捉变量声明等错误 use warnings; # 启用警告,帮助发现潜在问题# 遍历 1 到 9 的数字 for my $i (1..9) {# 对于每个 $i,遍历 1…...

Android--第一个android程序
写在前边 ※安卓开发工具常用模拟器汇总Android开发者必备工具-常见Android模拟器(MuMu、夜神、蓝叠、逍遥、雷电、Genymotion...)_安卓模拟器-CSDN博客 ※一般游戏模拟器运行速度相对较快,本文选择逍遥模拟器_以下是Android Studio连接模拟器实现(先从以上博文中…...

MySQL的并行复制原理
1. 并行复制的概念 并行复制(Parallel Replication)是一种通过同时处理多个复制任务来加速数据复制的技术。它与并发复制的区别在于,并行复制更多关注的是数据块或事务之间的并行执行,而不是单纯的任务并发。在数据库主从复制中&…...

2023年五一杯数学建模C题双碳目标下低碳建筑研究求解全过程论文及程序
2023年五一杯数学建模 C题 双碳目标下低碳建筑研究 原题再现: “双碳”即碳达峰与碳中和的简称,我国力争2030年前实现碳达峰,2060年前实现碳中和。“双碳”战略倡导绿色、环保、低碳的生活方式。我国加快降低碳排放步伐,大力推进…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...

企业大模型服务合规指南:深度解析备案与登记制度
伴随AI技术的爆炸式发展,尤其是大模型(LLM)在各行各业的深度应用和整合,企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者,还是积极拥抱AI转型的传统企业,在面向公众…...
