[LeetCode] 542. 01矩阵
题目描述:
给定一个由 0 和 1 组成的矩阵 mat ,请输出一个大小相同的矩阵,其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。
两个相邻元素间的距离为 1 。
示例 1:
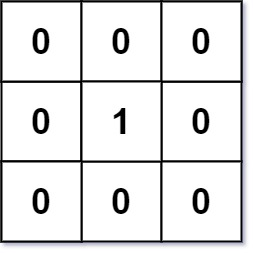
输入:mat = [[0,0,0],[0,1,0],[0,0,0]] 输出:[[0,0,0],[0,1,0],[0,0,0]]
示例 2:
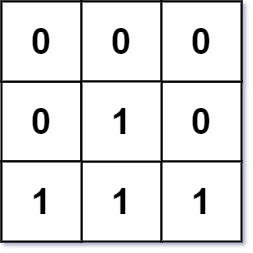
输入:mat = [[0,0,0],[0,1,0],[1,1,1]] 输出:[[0,0,0],[0,1,0],[1,2,1]]
提示:
m == mat.lengthn == mat[i].length1 <= m, n <= 1041 <= m * n <= 104mat[i][j] is either 0 or 1.mat中至少有一个0
题目链接:
. - 力扣(LeetCode)
解题主要思路:
这道题明显是bfs的一种,但是跟之前刷到的 "最短路径" 类题目又不太一样。准确的来说,之前刷到的 "最短路径" 类题目是端到端的bfs,而这道题是多个端到一个端的bfs,即多源bfs。如果按照之前的 "最短路径" 的方式来硬解的话,遍历原数组的时间复杂度是On,遍历原数组的时候进行bfs,时间复杂度是On2,这样下来时间复杂度来到了惊人的On的立方。
其实,我们可以换个思路,既然是多个端到一个端,那我们就反着来,从一个端一层一层往外扩到多个端。就以这题为例,多个端指的是1,一个端指的是0,我们就反着来,从0的位置一层一层往外扩。
解题代码:
class Solution {
public:int dx[4]{0, 0, 1, -1};int dy[4]{1, -1, 0, 0};vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {int m = mat.size(), n = mat[0].size();vector<vector<int>> ret(m, vector<int>(n, -1));queue<pair<int, int>> que;// 将0的坐标加入到队列中for (int i = 0; i < m; ++i) for (int j = 0; j < n; ++j) if (mat[i][j] == 0) {que.push(make_pair(i, j));ret[i][j] = 0;}// ret[x][y] == -1 原数组该下标元素为1且未遍历(外扩到)// ret[x][y] != -1 原数组该下标元素为0 or 该位置为1且已遍历// 一层一层往外扩while (que.size()) {auto [a, b] = que.front(); que.pop();for (int i = 0; i < 4; ++i) {int x = a + dx[i], y = b + dy[i];if (x >= 0 && x < m && y >= 0 && y < n && ret[x][y] == -1) {ret[x][y] = ret[a][b] + 1;que.push(make_pair(x, y));}}}return ret;}};相关文章:

[LeetCode] 542. 01矩阵
题目描述: 给定一个由 0 和 1 组成的矩阵 mat ,请输出一个大小相同的矩阵,其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。 两个相邻元素间的距离为 1 。 示例 1: 输入:mat [[0,0,0],[0,1,0],[0,0,0]] 输出…...

国产AI模型“Yi-Lightning”逆袭超越GPT-4!
近日,全球千万用户盲测投票产生的AI模型排行榜公布,令人惊喜的是,国产AI模型“Yi-Lightning”成功逆袭,一举超越了此前长期占据榜首的GPT-4。 Ai 智能办公利器 - Ai-321.com 人工智能 - Ai工具集 - 全球热门人工智能软件ai工具集…...

安卓設備上怎麼設置HTTP代理?
HTTP代理是一種仲介伺服器,它在用戶的設備和互聯網之間傳遞請求。通過HTTP代理,請求會先發送到代理伺服器,然後由代理伺服器轉發到目標網站。這樣,目標網站只會看到代理伺服器的IP地址,而不是真實IP地址。這種機制可以…...

学习Redisson实现分布式锁
官网:https://redisson.org/ 官方文档:https://redisson.org/docs/getting-started/ 官方中文文档:https://github.com/redisson/redisson/wiki/%E7%9B%AE%E5%BD%95 1、引入依赖 <!--redisson--> <dependency><groupId>or…...

2024CSP-J模拟赛9————S12678
一,赛中得分 T1100T2100T350T440总分290 二,赛中概括 T1T2较快过,T3T4骗了90分(意料之中,这么好骗分!!!)。 三,题目解析 涂格子(paint) 问题描述 现在有…...

HarmonyOS中ArkUi框架中常用的装饰器
目录 1.装饰器 1)Component 1--装饰内容 2)Entry 1--装饰内容 2--使用说明 3)Preview 1--装饰内容 2--使用说明 4)CustomDialog 1--装饰内容 2--使用说明 5)Observed 1--装饰内容 2--使用说明 6)ObjectLin…...

服务攻防之Redis数据库安全
最近我将会把一些服务攻防方面的姿势在这里做一个简单总结。欢迎大家留言讨论。 首先我们先对这类安全问题做一个总体的概括! 一、总概 1.服务判断: 端口扫描:利用服务开启后的目标端口开放判断 组合判断:利用搭建常见组合分析可能开放服务…...

随机森林算法的原理与实现
随机森林(Random Forest)是一种集成学习算法,它通过构建多个决策树并结合这些树的结果来进行分类或回归。与单一的决策树相比,随机森林通过集成多个树的结果,能够显著提高预测的准确性和稳定性,减少模型的过…...

模仿百度-基础版
<!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>百度案例</title><style>*{margin: 0;p…...

c++贴瓷砖
题目描述 有一块大小是 2 * n 的墙面,现在需要用2种规格的瓷砖铺满,瓷砖规格分别是 2 * 1 和 2 * 2,请计算一共有多少种铺设的方法。 输入 输入的第一行包含一个正整数T(T<20),表示一共有T组数据&…...
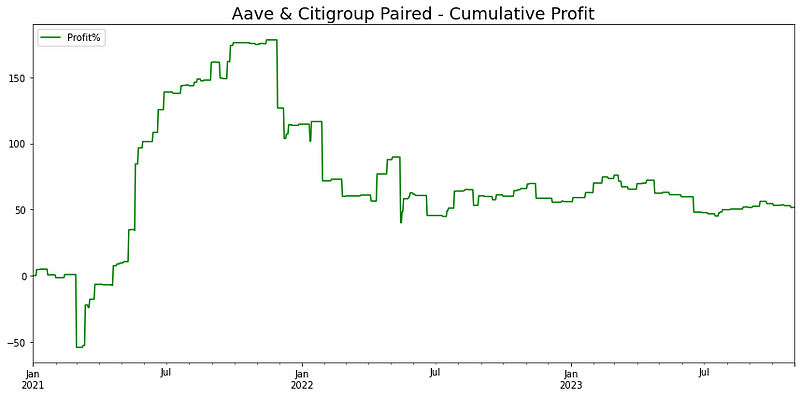
用 Python 构建高级配对交易策略
作者:老余捞鱼 原创不易,转载请标明出处及原作者。 写在前面的话: 本文阐述通过分析加密货币和传统金融工具之间的相关性和协整性,以及实施 Z-score 方法来生成交易信号,然后介绍如何使用 Python 构建配对交易策…...

Java 引用数据类型详解、字符串的不可变性、如何处理字符串的内存管理、String Pool 及其优化
文章目录 1. 引用数据类型1.1 常见引用数据类型 2. 字符串的不可变性2.1 不可变性的优点2.2 不可变性示例 3. 如何处理字符串的内存管理3.1 String Pool3.2 String 内存优化 4. String Pool 及其优化4.1 String Pool的工作原理4.2 String Pool的优化4.3 使用 intern() 进一步优…...

Babel使用
初始化项目 npm init -y 创建文件 // 转码前 // 定义数据 let input [1, 2, 3] // 将数组的每个元素 1 input input.map(item > item 1) console.log(input)配置.babelrc Babel的配置文件是.babelrc,presets字段设定转码规则,将es2015规则加入…...

自动机器学习(AutoML)
utoML是PAI的提供的自动寻找超参组合的机器学习增强型服务。您在训练模型时,如果超参组合复杂度过高,需大量训练资源和手工调试工作,可以使用AutoML来节省模型调参时间,提升模型调优效率和模型质量。 基础概念 超参数:…...

Vivado时序报告六:Report Timing详解
目录 一、前言 二、配置选项概览图 三、配置选项详解 3.1 Targets 3.2 Options 3.1.1 Report 3.1.2 Path limits 3.1.3 Path display 3.2 Advanced 3.2.1 Report 3.2.2 File Output 3.2.3 miscellaneous 3.3 Timer Settings 3.4 共有部分 四、 设计示例 4.1 设…...

java基础:数据类型的总结
一、Java 常用数据类型 1.数据类型分为:(1)基本数据类型 (2)引用数据类型 2.基本数据类型分类:数值型,非数值型。 3.数值型:(1) 整数类型(byte,short,int,long) (2) …...

【目标检测论文解读复现NO.39】基于改进 YOLOv8 的轻量级复杂环境苹果叶片病害检测方法
前言 此前出了目标改进算法专栏,但是对于应用于什么场景,需要什么改进方法对应与自己的应用场景有效果,并且多少改进点能发什么水平的文章,为解决大家的困惑,此系列文章旨在给大家解读最新目标检测算法论文,…...
)
python 基础笔记 2(函数, 类)
起因, 目的: 把很久以前,自己写的笔记发布出来。 现在粉丝多了,也不觉得丢人了。 为什么这些序号不连贯,因为有些很熟悉的东西,我都删了。 内建函数, 函数 zip()函数,利用 * 号操作符,可以将元组解压为列表。 我怀疑是zip的解包只能用一次。在内存中解开一次之后就销…...

LeetCode 2090.半径为K的子数组平均值
题目: 给你一个下标从 0 开始的数组 nums ,数组中有 n 个整数,另给你一个整数 k 。 半径为 k 的子数组平均值 是指:nums 中一个以下标 i 为 中心 且 半径 为 k 的子数组中所有元素的平均值,即下标在 i - k 和 i k 范…...
deleteLater的作用)
Qt C++ 编程中定义了一个槽函数(slot)deleteLater的作用
这行代码是在 Qt C编程中定义了一个槽函数(slot)deleteLater。 在 Qt 框架中,Q_SLOTS关键字用于声明类中的槽函数。deleteLater是一个非常有用的函数,它会安排接收对象在事件循环返回后被删除。 通常在以下情况下会使用deleteLa…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...
