2024CSP-J模拟赛9————S12678
一,赛中得分
| T1 | 100 |
| T2 | 100 |
| T3 | 50 |
| T4 | 40 |
| 总分 | 290 |
二,赛中概括
T1T2较快过,T3T4骗了90分(意料之中,这么好骗分!!!)。
三,题目解析
涂格子(paint)
问题描述
现在有一个 n 行 m 列的网格纸,一开始每个格子都是白色的。
现在你可以任意挑选恰好 x 行和 y 列,将挑选的整行(整列)上的每一个格子涂成黑色, 问剩下多少个格子是白色的。
输入格式
第一行为 n,m,x,y,含义如上所示。
输出格式
一行一个整数表示答案。
样例输入
5 3 1 2 样例输出
数据分布
4
对于 60% 的数据: 1≤n,m≤100 对于 100% 的数据: 1≤n,m≤10^9(1000000000),1≤x≤n,1≤y≤m
较简单,一道数学题(不脑残就能过)
AC代码
#include<bits/stdc++.h>
using namespace std;
int main(){freopen("paint.in","r",stdin);freopen("paint.out","w",stdout);long long n,m,x,y;cin>>n>>m>>x>>y;cout<<n*m-n*y-x*(m-y);//算出结果return 0;
}数串串(aba)
问题描述
给定一个长度为 n 的字符串,求有多少个长度为 3 的子序列满足形如 ABA 的格式,即子序列中的第一个字母等于第三个字母,但它们都不等于第二个字母。
由不同位置的相同字符构成的子序列被认为是不同的子序列,见样例解释。
一个序列被称为字符串 s 的子序列,当且仅当该序列能仅通过 s 删除一部分字符得到。
输入格式
第一行一个正整数 n 表示字符串的长度。
第二行一个长度为 n 的字符串,保证字符串仅由小写英文字母构成。
输出格式
一行一个整数表示答案。
样例输入
样例输出
7 abacabc
9 样例解释
满足条件的子序列有 aba,aba,aca,aca,bab,bab,bcb,cac,cbc 共 9 个。
数据分布
对于 10% 的数据满足 n≤300 ;
对于 60% 的数据满足 n≤5×10^4(50000) ;
对于 100% 的数据满足 1≤n≤10^6(1000000) 。
不会的人可以先参考一下两道题:
题目大意:
给定一个字符串,请计算
ac作为字符串子序列出现的次数注意:字符串子序列指的是从最初字符串通过去除某些元素但不破坏余下元素的相对位置(在前或在后)而形成的新序列。例如,
acf、bde、bcd都是abcdef的子序列,而cae并不是。样例:
输入:
aaaccc
输出:
9
题目解析:
可以从前往后计算有多少个a,把每个c的地方出现了几个a加起来;也可以从后往前计算有多少个c,把每个a的地方出现了几个c加起来。
AC代码:
#include <bits/stdc++.h> using namespace std; int main() {//freopen("acok.in","r",stdin);//freopen("acok.out","w",stdout);string a;cin>>a;int b=a.size(),cnt=0,ans=0;int c[b]={0};for(int i=0;i<b;i++){if(a[i]=='a'){ans++;}c[i]=ans;if(a[i]=='c')cnt+=c[i];}cout<<cnt;//fclose(stdin);//fclose(stdout);return 0; }扩展:输入长度和字符串,求里面有多少个cow。
思路:用枚举,循环在字符串中正序查找O左边C的个数,用枚举,循环在字符串中倒序查找O右边W的个数,把他们相乘,最后相加。
样例:
输入:
6
coowww
输出:
6
AC代码:
#include<bits/stdc++.h> using namespace std; long long c[100005],d[100005]; int main(){int n;cin>>n;string a;cin>>a;long long cnt=0,b=a.size();long long ans=0;for(int i=0;i<b;i++){if(a[i]=='C')ans++;c[i]=ans;}ans=0;for(int i=b-1;i>=0;i--){if(a[i]=='W')ans++;d[i]=ans;}for(int i=0;i<b;i++){if(a[i]=='O'){cnt+=c[i]*d[i];}}cout<<cnt;return 0; }与上面两道题的思路一样
AC代码
#include<bits/stdc++.h> using namespace std; long long n,b[1000006],c[1000006],cntt=0; int main(){freopen("aba.in","r",stdin);freopen("aba.out","w",stdout);string a;cin>>n>>a;for(char i='a';i<='z';i++){memset(b,0,sizeof(b));memset(c,0,sizeof(c));long long ans=0,cnt=0,sum=0;for(int j=0;j<n;j++){if(a[j]==i)ans++;b[j]=ans;}for(int j=n-1;j>=0;j--){if(a[j]==i)cnt++;c[j]=cnt;}for(int j=0;j<n;j++){if(a[j]!=i){sum+=c[j]*b[j];}}cntt+=sum;}cout<<cntt;return 0; }取石子(pick)
问题描述
有 n 堆石头排成一行,第 i 堆中有 ai 颗石子,Alice 和 Bob 打算玩一个取石子的博弈游戏,他们为每堆石子赋予了一个权值 bi,并规定一次操作为:选定一堆石子,从它本身和它前面的所有石子堆中各取走一颗。当前面有的石子堆中已经无石子的时候,不允许这样操作。对第 i 堆石子进行操作可以获得权值 bi。每堆石子对应的操作只能做 11 次。
现在他们不想玩无趣的博弈游戏了,他们想知道如果他们不断进行这样的操作,直到没有任何操作可以进行,在最优情况下,一共能获得多少权值。
形式化来说:给定 n 长序列 a1,a2,⋯,an,一次操作为选定一个 x,使a1,a2,⋯,ax 均减少 1,但不允许选择会将某个 ai 减成负数的 x,操作完成之后获得权值 bx,每种 x 最多只能被选定 1 次,求经过任意多次操作之后能获得的最大权值。
输入格式
第一行为石子堆数 n
第二行为 n 个整数 a1,a2,⋯,an
第三行为 n 个整数 b1,b2,⋯,bn
输出格式
一行一个整数,可获得的最大权值和
样例输入
56 2 2 1 11 3 2 4 5样例输出
9样例解释
可以对第 1,2,5 堆石子分别进行一次操作,共获得权值 1+3+5=9,最后的石子堆情况为 3 0 1 0 0
数据分布
对于 100% 的数据,1≤n≤5000,1≤ai≤10^9(1000000000),1≤bi≤10^5(100000)
对于 30% 的数据,有额外限制:1≤n≤20
对于另外 30% 的数据,有额外限制:对于所有的 i,bi=1
动态规划
AC代码
#include<bits/stdc++.h> using namespace std; long long n,a[5005],b[5005],cnt=0,dp[5005][5005]; int main(){//freopen("pick.in","r",stdin);//freopen("pick.out","w",stdout);cin>>n;for(int i=1;i<=n;i++){cin>>a[i];}for(int i=1;i<=n;i++){cin>>b[i];}memset(dp,-1,sizeof(dp));for(int i=0;i<=n;i++){dp[0][i]=0;}for(int i=1;i<=n;i++){for(long long j=0;j<=n;j++){dp[i][min(a[i],j)]=max(dp[i][min(a[i],j)],dp[i-1][j]);}if(a[i]>0){for(long long j=1;j<=n;j++){if(dp[i-1][j]!=-1)dp[i][min(a[i]-1,j-1)]=max(dp[i-1][j]+b[i],dp[i][min(a[i]-1,j-1)]);}}}for(int i=0;i<=n;i++){cnt=max(cnt,dp[n][i]);}cout<<cnt<<endl;return 0; }健身计划(gym)
问题描述
Setsuna 想要运动!
于是她安排了 n 天内的作息,作息用一个 01 字符串 s 表示,若 si 为 0 则表示这天休息,为 11 则表示这天要去健身房运动。
但是连续 x 天的运动会积累 x(x+1)/2 点疲劳值,也就是说字符串中每段长度为 x 的极长连续 1 会带来 x(x+1)/2 点疲劳值。
例如,若她的安排为 11101011 ,那疲劳值为 23(3+1)+21(1+1)+22(2+1)=10 点。
现在她可以把任意天运动日改成休息日,问最少需要改几天才能使得疲劳值小于等于 k。
输入格式
第一行包含两个整数 n,k 。
第二行包含一个长度为 n 的 01 串 s。
输出格式
输出一个整数,表示答案。
样例输入1
7 41110111样例输出1
2样例输入2
3 1111样例输出2
2数据分布
对于 15% 的数据满足 n≤15 ;
对于 40% 的数据满足 n≤300 ;
对于 60% 的数据满足 n≤2000 ;
对于 100% 的数据满足 1≤n≤10^5(100000),0≤k≤2n(n+1) 。
优先队列
AC代码
#include<bits/stdc++.h> using namespace std; long long n,m,cnt=0,t=0; long long pilao(long long x){return x*(x+1)/2; } long long cal(long long l,long long k){if(l<=k)return 0;l-=k;k++;return l%k*pilao(l/k+1)+(k-l%k)*pilao(l/k); } struct node{int len,k;node(int lenn=0,int kk=0){len=lenn;k=kk;}bool operator<(const node& p) const {long long x=cal(len,k)-cal(len,k+1);long long y=cal(p.len,p.k)-cal(p.len,p.k+1);return x<y;} }; priority_queue<node> q; int main(){//freopen("gym.in","r",stdin);//freopen("gym.out","w",stdout);int now=0;cin>>n>>m;for(int i=1;i<=n;i++){int x;scanf("%1d",&x);if(x)cnt++;if(!x||i==n){if(cnt){q.push(node(cnt,0));now+=pilao(cnt);}cnt=0;}}long long ans=0;while(now>m){ans++;node tmp=q.top();q.pop();now-=cal(tmp.len,tmp.k)-cal(tmp.len,tmp.k+1);q.push(node(tmp.len,tmp.k+1));}cout<<ans;return 0; }
相关文章:

2024CSP-J模拟赛9————S12678
一,赛中得分 T1100T2100T350T440总分290 二,赛中概括 T1T2较快过,T3T4骗了90分(意料之中,这么好骗分!!!)。 三,题目解析 涂格子(paint) 问题描述 现在有…...

HarmonyOS中ArkUi框架中常用的装饰器
目录 1.装饰器 1)Component 1--装饰内容 2)Entry 1--装饰内容 2--使用说明 3)Preview 1--装饰内容 2--使用说明 4)CustomDialog 1--装饰内容 2--使用说明 5)Observed 1--装饰内容 2--使用说明 6)ObjectLin…...

服务攻防之Redis数据库安全
最近我将会把一些服务攻防方面的姿势在这里做一个简单总结。欢迎大家留言讨论。 首先我们先对这类安全问题做一个总体的概括! 一、总概 1.服务判断: 端口扫描:利用服务开启后的目标端口开放判断 组合判断:利用搭建常见组合分析可能开放服务…...

随机森林算法的原理与实现
随机森林(Random Forest)是一种集成学习算法,它通过构建多个决策树并结合这些树的结果来进行分类或回归。与单一的决策树相比,随机森林通过集成多个树的结果,能够显著提高预测的准确性和稳定性,减少模型的过…...

模仿百度-基础版
<!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>百度案例</title><style>*{margin: 0;p…...

c++贴瓷砖
题目描述 有一块大小是 2 * n 的墙面,现在需要用2种规格的瓷砖铺满,瓷砖规格分别是 2 * 1 和 2 * 2,请计算一共有多少种铺设的方法。 输入 输入的第一行包含一个正整数T(T<20),表示一共有T组数据&…...
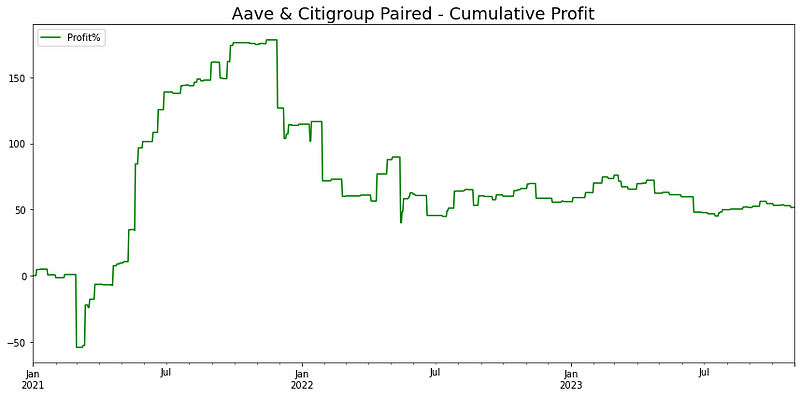
用 Python 构建高级配对交易策略
作者:老余捞鱼 原创不易,转载请标明出处及原作者。 写在前面的话: 本文阐述通过分析加密货币和传统金融工具之间的相关性和协整性,以及实施 Z-score 方法来生成交易信号,然后介绍如何使用 Python 构建配对交易策…...

Java 引用数据类型详解、字符串的不可变性、如何处理字符串的内存管理、String Pool 及其优化
文章目录 1. 引用数据类型1.1 常见引用数据类型 2. 字符串的不可变性2.1 不可变性的优点2.2 不可变性示例 3. 如何处理字符串的内存管理3.1 String Pool3.2 String 内存优化 4. String Pool 及其优化4.1 String Pool的工作原理4.2 String Pool的优化4.3 使用 intern() 进一步优…...

Babel使用
初始化项目 npm init -y 创建文件 // 转码前 // 定义数据 let input [1, 2, 3] // 将数组的每个元素 1 input input.map(item > item 1) console.log(input)配置.babelrc Babel的配置文件是.babelrc,presets字段设定转码规则,将es2015规则加入…...

自动机器学习(AutoML)
utoML是PAI的提供的自动寻找超参组合的机器学习增强型服务。您在训练模型时,如果超参组合复杂度过高,需大量训练资源和手工调试工作,可以使用AutoML来节省模型调参时间,提升模型调优效率和模型质量。 基础概念 超参数:…...

Vivado时序报告六:Report Timing详解
目录 一、前言 二、配置选项概览图 三、配置选项详解 3.1 Targets 3.2 Options 3.1.1 Report 3.1.2 Path limits 3.1.3 Path display 3.2 Advanced 3.2.1 Report 3.2.2 File Output 3.2.3 miscellaneous 3.3 Timer Settings 3.4 共有部分 四、 设计示例 4.1 设…...

java基础:数据类型的总结
一、Java 常用数据类型 1.数据类型分为:(1)基本数据类型 (2)引用数据类型 2.基本数据类型分类:数值型,非数值型。 3.数值型:(1) 整数类型(byte,short,int,long) (2) …...

【目标检测论文解读复现NO.39】基于改进 YOLOv8 的轻量级复杂环境苹果叶片病害检测方法
前言 此前出了目标改进算法专栏,但是对于应用于什么场景,需要什么改进方法对应与自己的应用场景有效果,并且多少改进点能发什么水平的文章,为解决大家的困惑,此系列文章旨在给大家解读最新目标检测算法论文,…...
)
python 基础笔记 2(函数, 类)
起因, 目的: 把很久以前,自己写的笔记发布出来。 现在粉丝多了,也不觉得丢人了。 为什么这些序号不连贯,因为有些很熟悉的东西,我都删了。 内建函数, 函数 zip()函数,利用 * 号操作符,可以将元组解压为列表。 我怀疑是zip的解包只能用一次。在内存中解开一次之后就销…...

LeetCode 2090.半径为K的子数组平均值
题目: 给你一个下标从 0 开始的数组 nums ,数组中有 n 个整数,另给你一个整数 k 。 半径为 k 的子数组平均值 是指:nums 中一个以下标 i 为 中心 且 半径 为 k 的子数组中所有元素的平均值,即下标在 i - k 和 i k 范…...
deleteLater的作用)
Qt C++ 编程中定义了一个槽函数(slot)deleteLater的作用
这行代码是在 Qt C编程中定义了一个槽函数(slot)deleteLater。 在 Qt 框架中,Q_SLOTS关键字用于声明类中的槽函数。deleteLater是一个非常有用的函数,它会安排接收对象在事件循环返回后被删除。 通常在以下情况下会使用deleteLa…...

【Hive】8-Hive性能优化及Hive3新特性
Hive性能优化及Hive3新特性 Hive表设计优化 Hive查询基本原理 Hive的设计思想是通过元数据解析描述将HDFS上的文件映射成表 基本的查询原理是当用户通过HQL语句对Hive中的表进行复杂数据处理和计算时,默认将其转换为分布式计算 MapReduce程序对HDFS中的数据进行…...

计算机前沿技术-人工智能算法-大语言模型-最新研究进展-2024-10-18
计算机前沿技术-人工智能算法-大语言模型-最新研究进展-2024-10-18 目录 文章目录 计算机前沿技术-人工智能算法-大语言模型-最新研究进展-2024-10-18目录1. On the Reliability of Large Language Models to Misinformed and Demographically-Informed Prompts2. SafeLLM: Dom…...

CTF(四)
导言: 本文主要讲述在CTF竞赛中,web类题目file_include。 靶场链接:攻防世界 (xctf.org.cn) 一,观察页面。 可以看到一段php代码。从则段代码中我们可以知道: 1,使用include引入check.php文件ÿ…...

智慧商城项目1-项目初始化创建
这是一个面向移动端的项目,先看看做了这个项目能收获什么,注意这是vue2的项目, 是个经典项目,能为未来学习vue3项目打下基础。 首先来说一下为啥是vue2,因为vue3还没有大范围普及,目前大部分企业还在用vue2…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...
