使用Matplotlib绘制极轴散点图
散点图对于理解数据可视化中变量之间的相互作用至关重要。虽然散点图经常在笛卡尔坐标中创建,但我们也可以使用Matplotlib在极轴上创建散点图。有了这个功能,人们可以以创新的方式查看圆形或角形数据,例如周期性趋势或定向模式。在本文中,我们将介绍在Python中使用Matplotlib在极轴上绘制散点图的概念,包括如何创建它们,可视化它们和自定义它们。
极轴上的散点图
极坐标通过它们与参考点(原点)的距离以及与参考轴(通常为正x轴)形成的角度来表示平面中的点,与笛卡尔坐标相反,笛卡尔坐标使用x和y轴。
让我们考虑一个简单的例子,其中我们有一个包含方向数据的数据集,例如不同时间的风向。我们希望在极坐标图上将这些数据可视化为散点。
在极轴上可视化散点图
import matplotlib.pyplot as plt
import numpy as np# Generating sample data
theta = np.linspace(0, 2*np.pi, 100)
r = np.random.rand(100) # Random radius values
colors = np.random.rand(100) # Random colors# Creating the polar scatter plot
plt.figure(figsize=(8, 8))
ax = plt.subplot(111, polar=True)
ax.scatter(theta, r, c=colors, s=100, cmap='hsv', alpha=0.75)plt.title('Scatter Plot on Polar Axis', fontsize=15)
plt.show()- 这段代码使用np.linspace创建了一个由100个等距角度组成的数组,这些角度在0到2π之间(整圆)。
- 这些角度表示极轴上数据点的位置。
- r使用np.random.rand生成一个0到1之间的100个随机数的数组,表示数据点沿径向轴距原点的距离。

数据点围绕极轴相当均匀地分散。θ值对应于点的角度,r值对应于点到原点的距离。距离原点较近的点用蓝色表示,而距离原点较远的点用红色表示。
极轴上的散点图,偏移原点
# Create the polar scatter plot with offset origin
plt.figure(figsize=(8, 8))
ax = plt.subplot(111, polar=True, theta_offset=np.pi/4) # Offset origin by pi/4
ax.scatter(theta, r, c=colors, s=100, cmap='hsv', alpha=0.75)plt.title('Scatter Plot on Polar Axis with Offset Origin', fontsize=15)
plt.show()
- 极轴上的散点图以圆形方式显示数据点。
- 偏移原点np.pi/4会移动绘图的起点,从而提供不同的参考。

使用极坐标绘制数据,其中每个点由角度(theta)和半径(r)表示。
- 图的原点偏移π/4弧度,这意味着零角度位于极轴上的45度标记处。
- 数据点由不同大小的彩色圆圈表示。
- 每个点的颜色由其色调、饱和度和值(HSV颜色模型)确定。
- 每个点的大小设置为100,透明度设置为0.75。
极轴上局限于扇形的散点图
# Create the polar scatter plot confined to a sector
plt.figure(figsize=(8, 8))
ax = plt.subplot(111, polar=True)
ax.scatter(theta, r, c=colors, s=100, cmap='hsv', alpha=0.75)# Confine scatter plot to a sector
ax.set_thetamin(45) # Minimum theta angle
ax.set_thetamax(135) # Maximum theta angleplt.title('Scatter Plot on Polar Axis Confined to a Sector', fontsize=15)
plt.show()- 此代码创建极散点图并将其限制在指定的扇区(45到135度)。
- set_thetamin和set_thetamax函数控制散点图的角度范围,提供指定扇区内的聚焦视图。

- 数据点根据色调饱和度值(HSV)色图着色,即每个点的颜色对应于其角度(theta)值。数据点的大小也是变化的,较大的点对应于较大的r值。
- 该图被限制在45度和135度之间的扇区,因为数据仅与该角度范围相关。
总结
总之,学习如何在Python中使用Matplotlib在极轴上绘制散点图,为显示方向或圆形数据模式提供了一种革命性的方法。
相关文章:

使用Matplotlib绘制极轴散点图
散点图对于理解数据可视化中变量之间的相互作用至关重要。虽然散点图经常在笛卡尔坐标中创建,但我们也可以使用Matplotlib在极轴上创建散点图。有了这个功能,人们可以以创新的方式查看圆形或角形数据,例如周期性趋势或定向模式。在本文中&…...

Elasticsearch入门:增删改查详解与实用场景
引言 在我之前做社交架构设计的时候,我们有一项关键且必要的需求:需要存储并记录用户的所有聊天记录。这些记录不仅用于业务需求,也承担了风控审查的职责。因此,在架构设计中,我们需要考虑每天海量的聊天消息量&#…...

【AI论文精读6】SELF-RAG(23.10)附录
【AI论文解读】【AI知识点】【AI小项目】【AI战略思考】 P1,P2,P3 附录 A SELF-RAG 细节 A.1 反思标记(reflection tokens) 反思标记的定义 下面我们提供了反思标记类型和输出标记的详细定义。前三个方面将在每个片段…...

sql-labs靶场第十七关测试报告
目录 一、测试环境 1、系统环境 2、使用工具/软件 二、测试目的 三、操作过程 1、寻找注入点 2、注入数据库 ①寻找注入方法 ②爆库,查看数据库名称 ③爆表,查看security库的所有表 ④爆列,查看users表的所有列 ⑤成功获取用户名…...

面试官:MySQL一次到底插入多少条数据合适啊?
前言 大家好!在互联网时代,我们的每一个动作,无论是浏览网页、分享动态、点赞、购物或者搜索信息,都会在背后产生数据。这些数据,根据其用途和重要性,可能会被储存到不同的地方,其中最常见的存…...
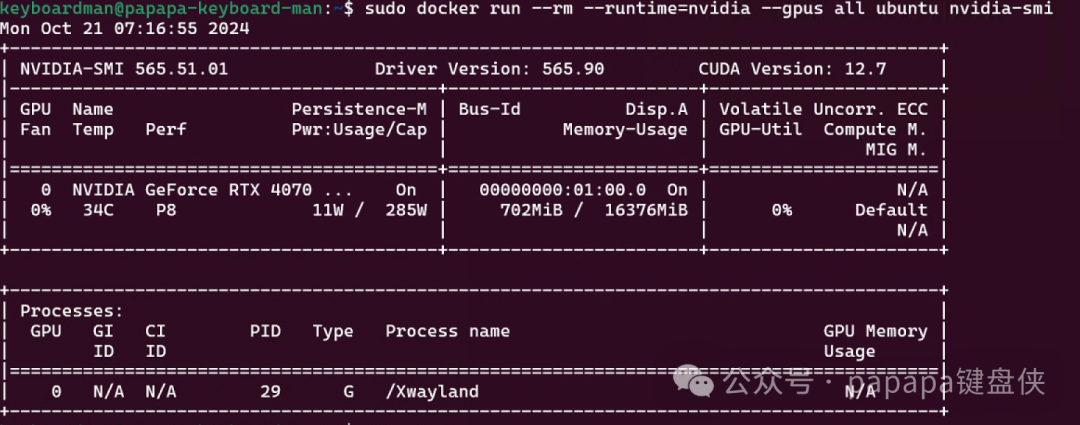
WSL2 构建Ubuntu系统-轻量级AI运行环境
环境:Win11 软件:WSL2 安装环境:Ubuntu 22.04 检查电脑是否开启虚拟化 打开:任务管理器->性能->CPU CPU 开启虚拟化(通常默认是开启的,如果没有开启需要BIOS开启) 虚拟化设置࿰…...

什么是凸二次规划问题
我们从凸二次规划的基本概念出发,然后解释它与支持向量机的关系。 一、凸二次规划问题的详细介绍 凸二次规划问题是优化问题的一类,目标是最小化一个凸的二次函数,受一组线性约束的限制。凸二次规划是一类特殊的二次规划问题,其…...

解决 Elasticsearch cluster_block_exception 错误的终极指南
Elasticsearch 是一个功能强大的分布式搜索引擎,广泛应用于全文检索、实时分析等场景。 尽管如此,像任何复杂系统一样,它也会遇到一些运行问题,其中较为常见且影响较大的就是 cluster_block_exception 错误。 本文将深入解析这种错…...

QT sql驱动错误QMYSQL driver not loaded
引用文章QMYSQL driver not loaded 根据引用文章,到在编译QT mysql.pro的源码步骤时,构建没有报错,但是在对应的文件夹内没有找到编译好的dll文件,经过全电脑搜寻,找到在此文件夹内。 遇到同样错误的朋友可以找找QT安…...

数据驱动,漫途能耗管理系统打造高效节能新生态!
在我国能源消耗结构中,工业企业所占能耗比例相对较大。为实现碳达峰、碳中和目标,工厂需强化能效管理,减少能耗与成本。高效的能耗管理系统通过数据采集与分析,能实时监控工厂能源使用及报警情况,为节能提供数据。构建…...
PH47代码框架软件二次开发极简教程
1. 教程说明 本教程适用于对飞控及Stm32程序设计比较熟悉的二次开发者快速掌握PH47框架的使用要点。本教程仅对PH47框架中最主要的二次开发特性进行简要说明,建议与框架中\DevStudio\Algorithms\Controller_Demo.cpp(.h)示例代码配合学习。关于二次开发特性中的详细…...

SQL Server-导入和导出excel数据-注意事项
环境: win10,SQL Server 2008 R2 之前写过的放在这里: SqlServer_陆沙的博客-CSDN博客 https://blog.csdn.net/pxy7896/category_12704205.html 最近重启ASP.NET项目,在使用sql server导出和导入数据时遇到一些问题,特…...

Linux系统:配置Apache支持CGI(Ubuntu)
配置Apache支持CGI 根据以下步骤配置,实现Apache支持CGI 安装Apache: 可参照文章: Ubuntu安装Apache教程。执行以下命令,修改Apache2配置文件000-default.conf: sudo vim /etc/apache2/sites-enabled/000-default.con…...

qt 序列化和反序列化
序列化:QByteArray buffer; QBuffer bufferDevice(&buffer); bufferDevice.open(QIODevice::WriteOnly); QDataStream out(&bufferDevice); out.setVersion(QDataStream::Qt_5_13); 反序列化: void deserialize(const QByteArray &buffer) {…...

java实现文件变动监听
在文件的内容发生变动时,应用可以感知这种变种,并重新加载文件内容,更新应用内部缓存 实现 轮询:定时器Timer,ScheduledExecutorService 判断文件修改:根据java.io.File#lastModified获取文件的上次修改时…...

Maven的使用
1. Maven 简介 https://maven.apache.org/ Maven 是一个强大的项目管理和构建工具,广泛应用于 Java 项目中,旨在简化项目的依赖管理、构建、测试、部署等工作。Maven 主要通过定义 pom.xml(Project Object Model 文件)来管理项…...

C++开发进阶1:C++编程命名规范
进行C开发时最基础且最重要的是命名规范,掌握良好的命名规范能增加代码的可读性。 认识文件: .cpp:C 源文件. .h或.hpp:C 头文件 .tpp模板实现文件(如果模板定义和实现分开) .inl内联文件,…...

Android 图片相识度比较(pHash)
概述 在 Android 中,要比对两张 Bitmap 图片的相似度,常见的方法有基于像素差异、直方图比较、或者使用一些更高级的算法如 SSIM(结构相似性)和感知哈希(pHash)。 1. 基于像素的差异比较 可以逐像素比较…...

Gitlab 完全卸载–亲测可行
1、停止gitlab gitlab-ctl stop2.卸载gitlab(注意这里写的是gitlab-ce) rpm -e gitlab-ce 3、查看gitlab进程 ps aux | grep gitlab 4、杀掉第一个进程(就是带有好多.............的进程) 5、删除所有包含gitlab文件 find / …...

gitlab操作和管理
详细的说明下这几条指令: Git global setup git config --global user.name “” git config --global user.email “” Create a new repository git clone ssh://git12/letect.git cd vlm-event-secondary-detect git switch -c main touch README.md git add RE…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...
