平面声波——一维Helmhotz波动方程
平面声波的一维Helmholtz波动方程是一种简化的声波传播模型,适用于在一维空间中传播的声波。
声波的基本物理过程---傅里叶变换---Helmholtz方程
一、声波的基本波动方程
在无源、无耗散、均匀介质中的一维声波的波动方程为:
其中:
表示位置
处和时间
时的声压,
是声波在介质中的传播速度,
表示声压对时间的二阶导数(即声压随时间的加速度),
表示声压对空间坐标的二阶导数(即声压随空间的变化率)。
二、Helmholtz方程的推导
为了将波动方程简化为Helmholtz方程,需假设声压随时间的变化具有简谐性质,即声波是单一频率的正弦波。即:
其中:
是只随空间位置
变化的函数,
是声波的角频率,
描述了声波的时间依赖部分,表示一个简谐振荡的形式。
将假设带入波动方程中,时间的二阶导数为:
代入波动方程:
由于时间部分是相同的,因此可以得到仅随空间
变化的方程:
三、一维Helmholtz波动方程
最终得到的方程称为一维Helmholtz波动方程,形式为:
其中:
是空间中的声压分布,
是波数,代表声波在空间中的传播特性。
四、 Helmholtz波动方程的解
一维Helmholtz方程的通解为:
其中:
和
是待定的常数,代表沿正向传播和沿反向传播的波,
和
分别代表波向正
方向和负
方向传播。
这种解形式表示声波可以在介质中沿不同方向传播,具体形式取决于边界条件(如吸声材料的反射特性等)。
相关文章:
平面声波——一维Helmhotz波动方程
平面声波的一维Helmholtz波动方程是一种简化的声波传播模型,适用于在一维空间中传播的声波。 声波的基本物理过程---傅里叶变换---Helmholtz方程 一、声波的基本波动方程 在无源、无耗散、均匀介质中的一维声波的波动方程为: 其中: 表示位…...
深度学习 简易环境安装(不含Anaconda)
在Windows上安装深度学习环境而不使用Anaconda,下面是一个基于pip的安装指南: 1. 安装Python 确保你已经安装了Python。可以从Python官网下载Python,并在安装时勾选“Add Python to PATH”选项。 注意,Python 不要安装最新版的…...
)
Java缓存技术(java内置缓存,redis,Ehcache,Caffeine的基本使用方法及其介绍)
目录 摘要 1. Java缓存技术概述 1.1定义 1.2 优势 1.3 应用场景 2. Java中的内置缓存实现 2.1 通过通过HashMap和ConcurrentHashMap实现缓存 3. Java缓存框架 3.1 Redis 3.1.1 redis的简介 3.1.4 Redis的工作原理 3.1.5 总结 3.2 Ehcache 3.2.1 Eh…...

YoloV9改进策略:主干网络改进|DeBiFormer,可变形双级路由注意力|全网首发
摘要 在目标检测领域,YoloV9以其高效和准确的性能而闻名。然而,为了进一步提升其检测能力,我们引入了DeBiFormer作为YoloV9的主干网络。这个主干网络的计算量比较大,不过,上篇双级路由注意力的论文受到很大的关注,所以我也将这篇论文中的主干网络用来改进YoloV9,卡多的…...

【力扣 | SQL题 | 每日3题】力扣2988,569,1132,1158
1 hard 3mid,难度不是特别大。 1. 力扣2988:最大部门的经理 1.1 题目: 表: Employees ---------------------- | Column Name | Type | ---------------------- | emp_id | int | | emp_name | varchar | | de…...

移动网络知识
一、3G网络 TD-SCDMA(时分同步码分多址接入)、WCDMA(宽带码分多址)和CDMA2000三种不同的3G移动通信标准 TD-SCDMA(时分同步码分多址接入):中国自主开发的一种3G标准主要用于国内市场ÿ…...

CentOS系统Nginx的安装部署
CentOS系统Nginx的安装部署 安装包准备 在服务器上准备好nginx的安装包 nginx安装包下载地址为:https://nginx.org/en/download.html 解压 tar -zxvf nginx-1.26.1.tar.gz执行命令安装 # 第一步 cd nginx-1.26.1# 第二步 ./configure# 第三步 make# 第四步 mak…...

Leetcode 最长公共前缀
java solution class Solution {public String longestCommonPrefix(String[] strs) {if(strs null || strs.length 0) {return "";}//用第一个字符串作为模板,利用indexOf()方法匹配,由右至左逐渐缩短第一个字符串的长度String prefix strs[0];for(int i 1; i …...

[C#][winform]基于yolov5的驾驶员抽烟打电话安全带检测系统C#源码+onnx模型+评估指标曲线+精美GUI界面
【重要说明】 该系统以opencvsharp作图像处理,onnxruntime做推理引擎,使用CPU进行推理,适合有显卡或者没有显卡windows x64系统均可,不支持macOS和Linux系统,不支持x86的windows操作系统。由于采用CPU推理,要比GPU慢。…...

【Flutter】基础入门:开发环境搭建
Flutter 是一个强大的跨平台框架,支持在 Android、iOS、Windows、Linux、Web 等多种平台上开发应用。下面将详细介绍如何在各个平台上构建 Flutter 开发环境,并使用相同的项目代码构建出一个可以在多个平台运行的跨平台 Demo。 Flutter 环境配置&#x…...
简介)
AI学习指南深度学习篇-对比学习(Contrastive Learning)简介
AI学习指南深度学习篇 - 对比学习(Contrastive Learning)简介 目录 引言对比学习的背景对比学习的定义对比学习在深度学习中的应用 无监督学习表示学习 详细示例 基本示例先进示例 对比学习的优缺点总结与展望 1. 引言 随着人工智能(AI&am…...

【蓝队技能】【规则开发1】Suricata-C2Webshell隧道
蓝队技能 Suricata-C2&Webshell&隧道 蓝队技能总结前言一、C2规则开发1.1 Sliver1.2 CS 二、内网隧道1.1 frps1.2 nps 三、webshell3.1 蚁剑3.2 冰蝎3.3 哥斯拉 总结 前言 本文聚焦于Suricata规则开发,提供针对Sliver、Cobalt Strike(CS…...
全面了解 NGINX 的负载均衡算法
NGINX 提供多种负载均衡方法,以应对不同的流量分发需求。常用的算法包括:最少连接、最短时间、通用哈希、随机算法和 IP 哈希。这些负载均衡算法都通过独立指令来定义,每种算法都有其独特的应用场景。 以下负载均衡方法(IP 哈希除…...

Java-继承与多态-上篇
关于类与对象,内容较多,我们分为两篇进行讲解: 📚 Java-继承与多态-上篇:———— <就是本篇> 📕 继承的概念与使用 📕 父类成员访问 📕 super关键字 📕 supe…...

通过比较list与vector在简单模拟实现时的不同进一步理解STL的底层
cplusplus.com/reference/list/list/?kwlist 当我们大致阅读完list的cplusplus网站的文档时,我们会发现它提供的接口大致上与我们的vector相同。当然的,在常用接口的简单实现上它们也大体相同,但是它们的构造函数与迭代器的实现却大有不同。…...

软件I2C的代码
I2C的函数 GPIO的配置——scl和sda都配置为开漏输出 void MyI2C_Init(void) {RCC_APB2PeriphClockCmd(RCC_APB2Periph_GPIOB,ENABLE);GPIO_InitTypeDef GPIO_InitStruture;GPIO_InitStruture.GPIO_Mode GPIO_Mode_Out_OD;GPIO_InitStruture.GPIO_PinGPIO_Pin_10 | GPIO_Pin_…...

登录时用户名密码加密传输(包含前后端代码)
页面输入用户名密码登录过程中,如果没有对用户名密码进行加密处理,可能会导致传输过程中数据被窃取,就算使用https协议,在浏览器控制台的Request Payload中也是能直接看到传输的明文,安全感是否还是不足。 大致流程&a…...

ai聊天对话页面-uniapp
流式传输打字机效果,只支持uniapp内使用 ,下载地址 https://download.csdn.net/download/qq_54123885/89899859...

虚拟滚动列表如何实现?
highlight: a11y-dark 虚拟滚动列表,虚拟滚动的关键在于只渲染当前视口内可见的数据项,而不是一次性渲染所有数据项。这可以显著提高性能,尤其是在处理大量数据时。 以下是一个完整的虚拟滚动列表的示例代码: <!DOCTYPE htm…...

07_Linux网络配置与管理:命令与工具指南
本系列文章导航:01_Linux基础操作CentOS7学习笔记-CSDN博客 文章目录 网络配置与管理:命令与工具指南1. ping命令2. ifconfig命令3. ip命令4. route命令5. ip route命令6. nslookup命令7. nmcli命令8. nmtui命令9. RHEL7修改网卡名1. 修改网络(会话)配置…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

高防服务器价格高原因分析
高防服务器的价格较高,主要是由于其特殊的防御机制、硬件配置、运营维护等多方面的综合成本。以下从技术、资源和服务三个维度详细解析高防服务器昂贵的原因: 一、硬件与技术投入 大带宽需求 DDoS攻击通过占用大量带宽资源瘫痪目标服务器,因此…...

基于Python的气象数据分析及可视化研究
目录 一.🦁前言二.🦁开源代码与组件使用情况说明三.🦁核心功能1. ✅算法设计2. ✅PyEcharts库3. ✅Flask框架4. ✅爬虫5. ✅部署项目 四.🦁演示效果1. 管理员模块1.1 用户管理 2. 用户模块2.1 登录系统2.2 查看实时数据2.3 查看天…...
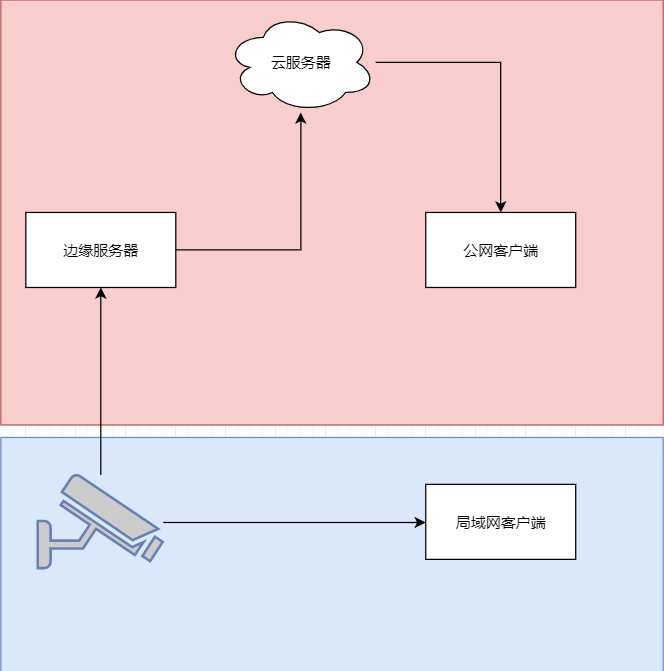
java 局域网 rtsp 取流 WebSocket 推送到前端显示 低延迟
众所周知 摄像头取流推流显示前端延迟大 传统方法是服务器取摄像头的rtsp流 然后客户端连服务器 中转多了,延迟一定不小。 假设相机没有专网 公网 1相机自带推流 直接推送到云服务器 然后客户端拉去 2相机只有rtsp ,边缘服务器拉流推送到云服务器 …...
