【数据结构与算法】之二分查找
二分查找(Binary Search)是一种在有序数组中查找特定元素的搜索算法。它通过比较数组中间元素与目标值来工作,从而将搜索范围缩小到一半,也称折半查找,是一种非常高效的工作于有序数组的查找算法。本文主要介绍二分查找及其几个变种,包括基础版、改变版、平衡版和Java版,以及Leftmost与Rightmost的概念。这些变种可能涉及对基本二分查找算法的优化或特定应用场景的调整。均采用Java语言实现。
一、基本原理

-
a 初始化:设置两个指针,一个指向数组的开始(i),另一个指向数组的结束(j)。
-
b 循环:当 i 小于或等于 j 时,执行以下操作:
- b1 计算中间位置 m:m = i + (j - i) / 2(建议采用 m = (i + j) >>> 1)。
- b2 比较中间元素 array[m] 与目标值:
- 如果 array[m] 等于目标值,则查找成功,返回m。
- 如果 array[m] 小于目标值,则将 i 更新为 m + 1,继续在数组的右半部分查找。
- 如果 array[m] 大于目标值,则将 j 更新为 m - 1,继续在数组的左半部分查找。
-
c 结束:如果循环结束时没有找到目标值,则返回一个表示失败的标志(通常是-1)。
二分查找的时间复杂度为O(log n),其中n是数组中的元素数量。这使得它在处理大数据集时非常高效。然而,二分查找要求数组必须是有序的,否则无法正确工作。
小细节:
在Java中,使用 >>> 无符号右移操作符来计算两个整数的平均值而不使用 “( j + i ) / 2” ,主要是出于以下几个原因:
-
避免溢出:当处理较大整数时,直接相加可能导致整数溢出。使用无符号右移可以避免这个问题,因为它不会进行实际的加法运算,而是通过位移来实现除以2的效果。
-
效率:位操作通常比算术操作更快。在性能敏感的应用中,使用位操作可以提高代码的执行效率。
-
整数除法:在Java中,整数除法会向下取整,这意味着如果两个数的和是奇数,直接除以2会得到一个较小的整数。使用无符号右移可以确保结果是一个整数,并且是两个数的中间值。
-
保持二进制位的对齐:在二分查找算法中,通常需要计算数组的中间索引。使用无符号右移可以确保计算出的中间索引是数组索引的有效值,避免了可能的负索引或越界问题。
示例代码
在二分查找中,我们通常需要计算数组的中间索引,如下所示:
int low = 0;
int high = array.length - 1;
while (low <= high) {
int mid = (low + high) >>> 1; // 进行比较和搜索操作
}在这个例子中,low 和 high 分别是搜索范围的起始和结束索引。使用 >>> 确保了即使 low 和 high 的和是一个奇数,计算出的 mid 也是一个有效的整数索引。(Java会自动将结果向下取整)
注意事项
- 负数处理:如果 low 或 high 是负数,使用无符号右移可能会导致不正确的结果,因为无符号右移会忽略符号位。在二分查找中,通常 low 和 high 都是非负数,所以这个问题不常见。
- 数据类型:确保使用的数据类型可以容纳计算结果。在Java中,整数溢出会导致意想不到的行为,尽管使用无符号右移可以减少溢出的风险。
总的来说,使用 >>> 无符号右移在Java中计算两个整数的平均值,是一种高效且安全的方法,特别是在需要处理大量数据或性能敏感的场合。
二、二分查找的各种形式
1) 基础版
在有序数组 A 内,查找值 target
-
如果找到返回索引
-
如果找不到返回 -1
public static int binarySearch(int[] a, int target) {int i = 0, j = a.length - 1;while (i <= j) {int m = (i + j) >>> 1;if (target < a[m]) { // 在左边j = m - 1;} else if (a[m] < target) { // 在右边i = m + 1;} else {return m;}}return -1;
}-
i,j 对应着搜索区间 [0,a.length-1](注意是闭合的区间),i<=j 意味着搜索区间内还有未比较的元素,i,j 指向的元素也可能是比较的目标
-
思考:如果不加 i==j 行不行?
-
回答:不行,因为这意味着 i,j 指向的元素会漏过比较
-
-
m 对应着中间位置,中间位置左边和右边的元素可能不相等(差一个),不会影响结果
-
如果某次未找到,那么缩小后的区间内不包含 m
2) 改变版
另一种写法
在有序数组 A 内,查找值 target
-
如果找到返回索引
-
如果找不到返回 -1

public static int binarySearch(int[] a, int target) {int i = 0, j = a.length;while (i < j) {int m = (i + j) >>> 1;if (target < a[m]) { // 在左边j = m;} else if (a[m] < target) { // 在右边i = m + 1;} else {return m;}}return -1;
}-
i,j 对应着搜索区间 [0,a.length)(注意是左闭右开的区间),i<j 意味着搜索区间内还有未比较的元素,j 指向的一定不是查找目标
-
思考:为什么这次不加 i==j 的条件了?
-
回答:这回 j 指向的不是查找目标,如果还加 i==j 条件,就意味着 j 指向的还会再次比较,找不到时,会死循环
-
-
如果某次要缩小右边界,那么 j=m,因为此时的 m 已经不是查找目标了
3) 平衡版
在有序数组 A 内,查找值 target
-
如果找到返回索引
-
如果找不到返回 -1

public static int binarySearchBalance(int[] a, int target) {int i = 0, j = a.length;while (1 < j - i) {int m = (i + j) >>> 1;if (target < a[m]) {j = m;} else {i = m;}}return (a[i] == target) ? i : -1;
}思想:
-
左闭右开的区间,i 指向的可能是目标,而 j 指向的不是目标
-
不奢望循环内通过 m 找出目标, 缩小区间直至剩 1 个, 剩下的这个可能就是要找的(通过 i)
-
j - i > 1 的含义是,在范围内待比较的元素个数 > 1
-
-
改变 i 边界时,它指向的可能是目标,因此不能 m+1
-
循环内的平均比较次数减少了
-
时间复杂度 log(n)
4) Java 版
以下是Java内部的二分查找算法
private static int binarySearch0(long[] a, int fromIndex, int toIndex,long key) {int low = fromIndex;int high = toIndex - 1;
while (low <= high) {int mid = (low + high) >>> 1;long midVal = a[mid];
if (midVal < key)low = mid + 1;else if (midVal > key)high = mid - 1;elsereturn mid; // key found}return -(low + 1); // key not found.
}-
例如 [1,3,5,6] 要插入 2 那么就是找到一个位置,这个位置左侧元素都比它小
-
等循环结束,若没找到,low 左侧元素肯定都比 target 小,因此 low 即插入点
-
-
插入点取负是为了与找到情况区分
-
-1 是为了把索引 0 位置的插入点与找到的情况进行区分
5) Leftmost 与 Rightmost (最左和最右)
有时我们希望返回的是最左侧的重复元素,如果用 基础二分查找
-
对于数组 [1, 2, 3, 4, 4, 5, 6, 7],查找元素4,结果是索引3
-
对于数组 [1, 2, 4, 4, 4, 5, 6, 7],查找元素4,结果也是索引3,并不是最左侧的元素

以下是返回最左侧元素索引:
public static int binarySearchLeftmost1(int[] a, int target) {int i = 0, j = a.length - 1;int candidate = -1;while (i <= j) {int m = (i + j) >>> 1;if (target < a[m]) {j = m - 1;} else if (a[m] < target) {i = m + 1;} else {candidate = m; // 记录候选位置j = m - 1; // 继续向左}}return candidate;
}以下是返回最右侧元素索引:

public static int binarySearchRightmost1(int[] a, int target) {int i = 0, j = a.length - 1;int candidate = -1;while (i <= j) {int m = (i + j) >>> 1;if (target < a[m]) {j = m - 1;} else if (a[m] < target) {i = m + 1;} else {candidate = m; // 记录候选位置i = m + 1; // 继续向右}}return candidate;
}6) Leftmost 与 Rightmost 的改动版
对于 Leftmost 与 Rightmost,可以返回一个比 -1 更有用的值,小于 traget的元素个数
Leftmost 改为
public static int binarySearchLeftmost(int[] a, int target) {int i = 0, j = a.length - 1;while (i <= j) {int m = (i + j) >>> 1;if (target <= a[m]) {j = m - 1;} else {i = m + 1;}}return i;
}-
小于等于中间值,都要向左找
Rightmost 改为
public static int binarySearchRightmost(int[] a, int target) {int i = 0, j = a.length - 1;while (i <= j) {int m = (i + j) >>> 1;if (target < a[m]) {j = m - 1;} else {i = m + 1;}}return i - 1;
}-
大于等于中间值,都要向右找
以上就是关于二分查找算法的各个版本,感谢各位看官的观看,下期见,谢谢~
相关文章:

【数据结构与算法】之二分查找
二分查找(Binary Search)是一种在有序数组中查找特定元素的搜索算法。它通过比较数组中间元素与目标值来工作,从而将搜索范围缩小到一半,也称折半查找,是一种非常高效的工作于有序数组的查找算法。本文主要介绍二分查找…...

vue修饰符
表单修饰符 1、lazy <input type "text" v-model.lazy "value"> <p>{{value}}</p>lazy跟懒加载类似,只有再说鼠标离开光标的时候才会触发,也就是说在input事件的oninput书法的时候不会赋值,当onch…...

Oracle里面,with ... as 用法介绍
在Oracle数据库中,WITH AS 子句(也称为公用表表达式,CTE, Common Table Expression)是一种在查询中定义临时结果集的方法。这个临时结果集可以在后续的查询中被引用,就像是一个临时的表或视图一样。使用 WITH AS 子句可…...

一个简单的Qt Console Application计算练习程序
初步体验Qt Creator 用途:练习20以内2位数乘法速算的程序 功能1:支持用户设定题目数量 std::cout << "请输入本次练习题目数量:";int numProblems 0;std::string num;std::cin >> num;try {numProblems std::stoi(…...

windows文件拷贝给wsl2的Ubuntu
参考: windows文件如何直接拖拽到wsl中_win 移到文件到wsl-CSDN博客 cp -r /mnt/盘名/目标文件 要复制到wsl中的位置e.g.cp -r /mnt/d/byt5 /home Linux文件复制、移动、删除等操作命令_linux移动命令-CSDN博客 Linux 文件、文件夹的复制、移动、删除 - Be-myse…...

vivado 采用 SSI 器件进行设计
SSI 管脚的考虑因素 在为特定 SLR 中的组件规划管脚时,请将引脚放置在同一个 SLR 中。例如,将器件的 DNA 信息作为外部接口的一部分 时,请将该接口的引脚放置在 DNA_PORT 所在的主 SLR 中。其它考虑因素包括如下: • 把…...

Lua环境安装
软考鸭微信小程序 学软考,来软考鸭! 提供软考免费软考讲解视频、题库、软考试题、软考模考、软考查分、软考咨询等服务 Lua是一种轻量级、小巧且易于嵌入应用程序的脚本语言,广泛用于游戏开发、Web开发、自动化脚本等领域。本文将详细介绍如何在不同操作系统上安装L…...

浏览器控制的无线开关
esp32-c3 作为HTTP server 控制led 灯。服务器注册两个uri 。一个"/open" 控制开,一个"/close"控制关。下一步再用一片c3作为客户端,运行http client 发送/open. /Close 模拟浏览器,控制led. 其实只要用手机或pc或平…...
Docker部署SSM项目及避坑指南
#又踩坑了,这里记录一下,以免日后忘记 前言:本来以为用docker部署个项目很轻松,嗯结果,又踩坑了,这里记录一个完整版。话不多说,开整。 第一步: 用docker拉取MySQL和Tomcat&#…...

多线程代码案例:单例模式/阻塞队列/线程池/定时器
案例一.单例模式 单例模式是一种设计模式;类似于棋谱,有固定套路,针对一些特定场景可以给出一些比较好的解决方案; 只要按照设计模式来写代码,就可以保证代码不会太差,保证了代码的下限; --------------------------------------------------------------------------------…...

Ruby CGI Cookie
Ruby CGI Cookie 在Web开发中,Cookie是一种常用的技术,用于在用户浏览器和服务器之间存储和传递信息。Ruby作为一种流行的编程语言,提供了CGI(Common Gateway Interface)库来处理Cookie。本文将详细介绍如何在Ruby中使用CGI库来创建、读取、修改和删除Cookie。 Cookie的…...

linux中取消anaconda默认使用base环境
在linux新安装anaconda之后,每次打开终端,总是显示正在使用默认anaconda中的base环境,如下如所示: 取消该默认设置,打开home目录下的.condarc文件,在末尾添加如下命令: auto_activate_base: fa…...

江门中微子到底是做什么的?
江门中微子实验是一项重要的大科学装置实验。以下是关于它的一些详细信息: 实验位置与建设深度:位于广东江门地下 700 米处。这样的深度可以有效屏蔽宇宙射线等外界干扰,为探测中微子提供较为纯净的实验环境。探测器特点: 拥有世界…...

React源码03 - React 中的更新
03 - React 中的更新 React 中创建更新的方式: 初次渲染:ReactDOM.render、ReactDOM.hydrate 后续更新:setState、forceUpdate 1. ReactDOM.render() 先创建 ReactRoot 顶点对象然后创建 FiberRoot 和 RootFiber创建更新,使应用进…...
)
【Hive实战】Hive MetaStore升级调研(Mysql)
Hive MetaStore升级调研(Mysql库) 文章目录 Hive MetaStore升级调研(Mysql库)升级步骤脚本说明原文 MetaStore升级的主要部分是对存储媒介mysql进行schema进行升级。 升级步骤 关闭MetaStore实例并限制对MetaStore MySQL数据库的访…...

优化漏洞扫描流程以保障企业数字化业务安全
漏洞扫描技术历经二十余年发展,已从人工搜索演进至开源及商业扫描平台,其应用紧随IT环境与数字业务变迁而不断革新。为有效提升漏洞检测效果,确保企业数字化业务安全运行,安全专家建议遵循以下关键步骤实施漏洞扫描: …...

【大数据算法】一文掌握大数据算法之:大数据算法分析技术。
大数据算法分析技术 1、引言2、 大数据分析技术2.1 时间/空间复杂度2.2 I/O 复杂度2.3 结果质量2.4 通信复杂度 3、总结 1、引言 小屌丝:鱼哥,最近更文有些不频繁了哈。 小鱼:这一个月不见,你这说话方式也变了。 小屌丝ÿ…...

使用AITemplate和AMD GPU的高效图像生成:结合Stable Diffusion模型
Efficient image generation with Stable Diffusion models and AITemplate using AMD GPUs 2024年1月24日,作者是[Douglas Jia] Stable Diffusion 已成为图像生成领域的突破性进展,帮助用户将文本描述转化为引人入胜的视觉输出。 Stable Diffusion 的…...

基于yolov10的驾驶员抽烟打电话安全带检测系统python源码+pytorch模型+评估指标曲线+精美GUI界面
【算法介绍】 基于YOLOv10的驾驶员抽烟、打电话、安全带检测系统是一种先进的驾驶行为监测系统。该系统利用YOLOv10算法的高效性和准确性,实现对驾驶员行为的实时检测与识别。 YOLOv10是一种最新的实时物体检测模型,其通过深度学习技术,如卷…...

虚拟机网络设置为桥接模式
1、打开VMware Workstation Pro,点击“虚拟机—设置”,进入虚拟机设置页面 2、点击“网络适配器”,网络连接选择桥接模式 3、点击“编辑—虚拟网络编辑器”,进入虚拟网络编辑器页面 4、选择桥接模式,并选择要桥接到的…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...
OPENCV图形计算面积、弧长API讲解(1)
一.OPENCV图形面积、弧长计算的API介绍 之前我们已经把图形轮廓的检测、画框等功能讲解了一遍。那今天我们主要结合轮廓检测的API去计算图形的面积,这些面积可以是矩形、圆形等等。图形面积计算和弧长计算常用于车辆识别、桥梁识别等重要功能,常用的API…...
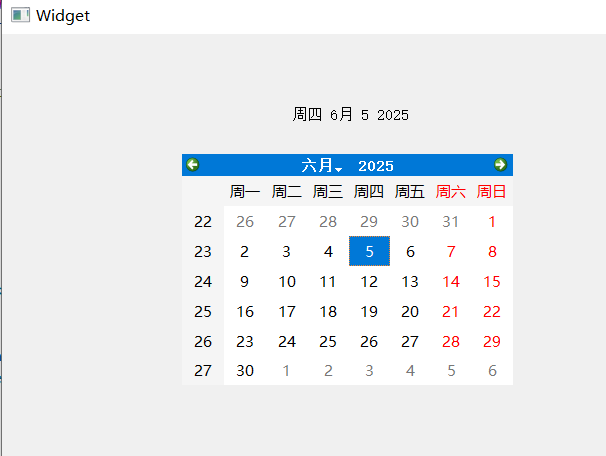
【QT控件】显示类控件
目录 一、Label 二、LCD Number 三、ProgressBar 四、Calendar Widget QT专栏:QT_uyeonashi的博客-CSDN博客 一、Label QLabel 可以用来显示文本和图片. 核心属性如下 代码示例: 显示不同格式的文本 1) 在界面上创建三个 QLabel 尺寸放大一些. objectName 分别…...
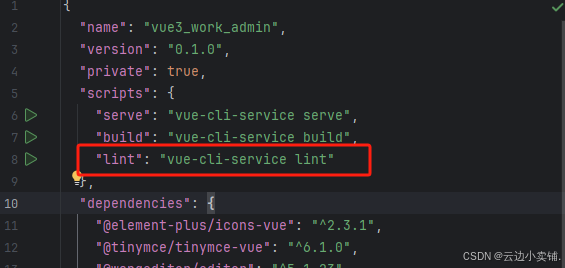
运行vue项目报错 errors and 0 warnings potentially fixable with the `--fix` option.
报错 找到package.json文件 找到这个修改成 "lint": "eslint --fix --ext .js,.vue src" 为elsint有配置结尾换行符,最后运行:npm run lint --fix...

react-pdf(pdfjs-dist)如何兼容老浏览器(chrome 49)
之前都是使用react-pdf来渲染pdf文件,这次有个需求是要兼容xp环境,xp上chrome最高支持到49,虽然说iframe或者embed都可以实现预览pdf,但为了后续的定制化需求,还是需要使用js库来渲染。 chrome 49测试环境 能用的测试…...

性能优化中,多面体模型基本原理
1)多面体编译技术是一种基于多面体模型的程序分析和优化技术,它将程序 中的语句实例、访问关系、依赖关系和调度等信息映射到多维空间中的几何对 象,通过对这些几何对象进行几何操作和线性代数计算来进行程序的分析和优 化。 其中࿰…...
