React中在map遍历中,给虚拟标签(<></>)加key
有时我们可能会需要在遍历时使用虚拟标签包裹内容,而不使用实际标签 ,这种时候会有一个问题,就是虚拟标签无法加key,这样控制台会一直有警告。
{[1,2,3,4].map(v=><><div></div><div></div><div></div></>)
}我们可以将虚拟标签换成这种形势,就能正常加key了
{[1,2,3,4].map(v=><React.Fragment key={'key'}><div></div><div></div><div></div></React.Fragment>)
}相关文章:
加key)
React中在map遍历中,给虚拟标签(<></>)加key
有时我们可能会需要在遍历时使用虚拟标签包裹内容,而不使用实际标签 ,这种时候会有一个问题,就是虚拟标签无法加key,这样控制台会一直有警告。 {[1,2,3,4].map(v><><div></div><div></div><…...

大数据生态守护:Hadoop的深度保护策略
PART 1 从Hadoop运行原理透视数据保护需求 1、Hadoop的定义与范畴 Hadoop,狭义而言,是一个专为大数据设计的分布式存储与计算平台,其核心组件包括HDFS(Hadoop分布式文件系统)、MapReduce(分布式计算框架&a…...
.因为这样就成了浮点值了,得不到准确数)
代码欣赏之:此题易错在 a+b 非要写成 a-fabs(b).因为这样就成了浮点值了,得不到准确数
代码欣赏之:此题易错在 ab 非要写成 a-fabs(b).因为这样就成了浮点值了,得不到准确数 7-23 小孩子才做选择,大人全都要 #include<stdio.h> #include<math.h> int main() {int a,b;scanf("%d %d",&a,&b);if(a&…...
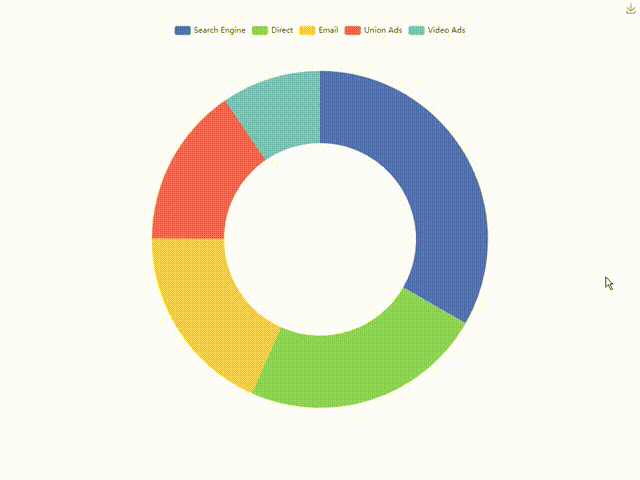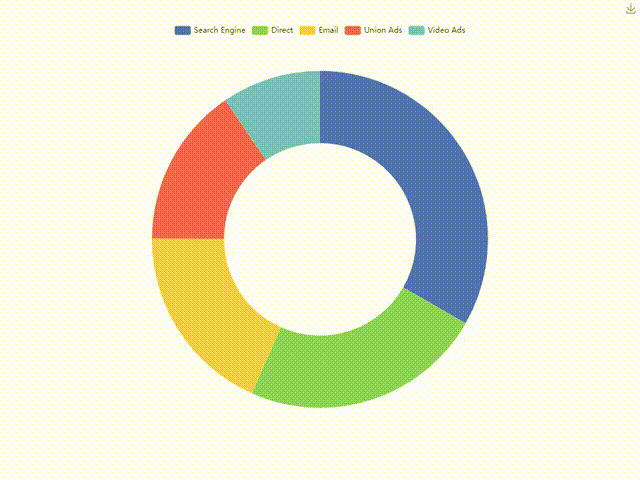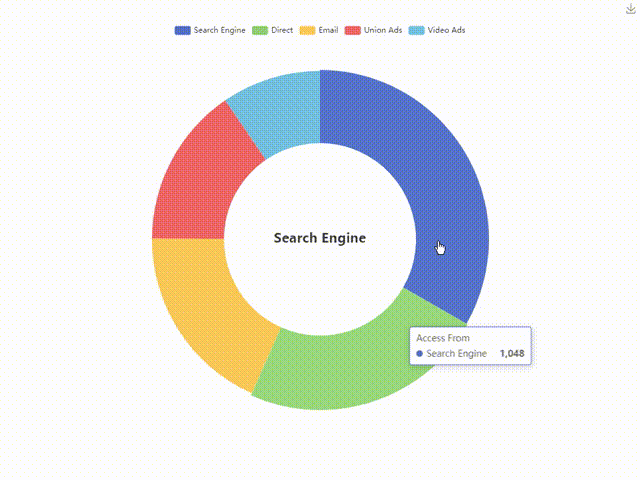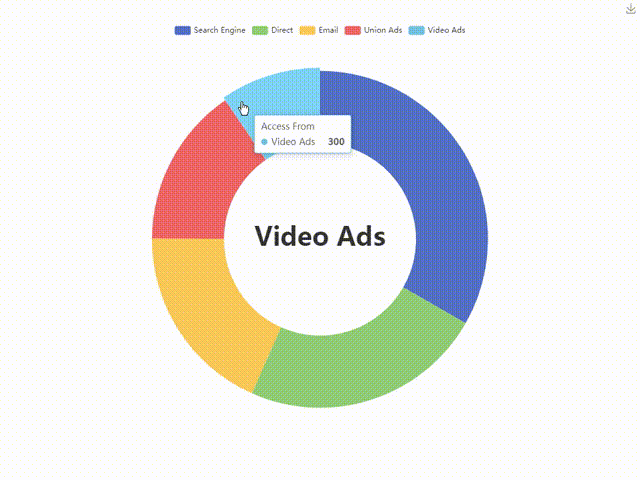
ECharts饼图-环形图,附视频讲解与代码下载
引言: 在数据可视化的世界里,ECharts凭借其丰富的图表类型和强大的配置能力,成为了众多开发者的首选。今天,我将带大家一起实现一个饼图图表,通过该图表我们可以直观地展示和分析数据。此外,我还将提供详…...
arcgis js 怎么加载geoserver发布的wms服务
arcgis js api加载wms服务,官方的参考样例: WMSLayer | Sample Code | ArcGIS Maps SDK for JavaScript 4.30 | Esri Developer 按照官方样例加载比较奇怪,我们平常习惯用url或者json的方式加载,稍微改一下就行,如下…...

前端_006_Vue2
文章目录 vue常用属性生命周期模版语法自定义组件全局注册 单文件组件路由 本文全部参考Vue2 简介:Vue是一个数据响应式,MVVM模型的JS框架 官网:https://v2.cn.vuejs.org/v2/guide/ API:https://v2.cn.vuejs.org/v2/api/#method…...

论多端数据互通网游的架构评估
摘要 在2023年,笔者参与了一款多端数据互通网络游戏的架构评估工作,并担任评估团队的核心成员。该游戏支持PC、移动设备和游戏机等多种终端,实现了数据的实时互通。本文通过该项目的评估实践,探讨了多端数据互通网游架构评估的关…...

网页HTML编写练习:华语榜中榜
网页效果 HTML代码 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta name"viewport" content"widthdevice…...
 和 `unordered_map`(无序映射))
C++ 编程基础:深入理解 `pair`(键值对) 和 `unordered_map`(无序映射)
C 编程基础:深入理解 pair(键值对) 和 unordered_map(无序映射) 在 C 标准库中,pair(键值对)和 unordered_map(无序映射)是两种常用的数据结构,它…...

高德动态地图
1.搭建页面结构 <div class"dataAllBorder02" style"position: relative; overflow: hidden;"><div class"map_title_box" style"height: 6%"><div class"map_title_innerbox"><div class"map_t…...

springboot集成camunda学习与使用
springboot集成camunda学习与使用.md 0、前言一、Spring Boot 集成camunda流程引擎1.新建全新的springboot工程2.添加pom.xml依赖3.启动Spring Boot工程4.切换成mysql数据库5.设计并部署一个BPMN流程6.camunda流程引擎测试6.1 通过camunda web控制台测试6.2 通过camunda rest接…...

微服务架构学习笔记
#1024程序员节|征文# 微服务架构作为现代软件开发中的热门技术架构,因其灵活性和可扩展性,逐渐成为许多企业系统设计的首选。以下是关于微服务的一些学习笔记,涵盖微服务的核心概念、优缺点、设计原则以及常用工具等方面。 1. 微服务是什么&…...

代码优化之简化if臃肿的判断条件
简化if判断条件 方法1: #include <iostream> #include <vector> #include <functional>// 封装参数的结构体 struct ConditionParams {int facenum;double zoomRatio;int iso;double facelv;int face_w;double qualityScore;int xx;int yy; };//…...

【OpenAI】第六节(语音生成与语音识别技术)从 ChatGPT 到 Whisper 的全方位指南
前言 在人工智能的浪潮中,语音识别技术正逐渐成为我们日常生活中不可或缺的一部分。随着 OpenAI 的 Whisper 模型的推出,语音转文本的过程变得前所未有的简单和高效。无论是从 YouTube 视频中提取信息,还是将播客内容转化为文本,…...

Docker 下备份恢复oracle
1.docker导出容器镜像 ##docker save -o 导出后的镜像名称.tar 容器名称|镜像id docker save -o oracle_11g.tar 3fa112fd3642 2.下载镜像上传镜像略 3.加载镜像 ##docker load -i <archive_file> docker load -i oracle11g11201.tar 4.添加版本号…...

oneplus3t-android_framework
0.确认oneplus6 root正常 oneplus6 root材料 oneplus6手机恢复出厂设置 , 或者 线刷 enchilada_22_K.52_210716_repack--HOS-10.0.11.zip : https://gitee.com/OnePlus6-brick-enchilada_22_K_52_210716_repack-HOS-10_0_11-zip OnePlus6Hydrogen_22…...

偷懒总结篇|贪心算法|动态规划|单调栈|图论
由于这周来不及了,先过一遍后面的思路,具体实现等下周再开始详细写。 贪心算法 这个图非常好 122.买卖股票的最佳时机 II(妙,拆分利润) 把利润分解为每天为单位的维度,需要收集每天的正利润就可以,收集正利润的区间…...

C语言初阶七:C语言操作符详解(1)
#1024程序员节|征文# 这篇文章是对之前文章中操作符的补充,可以看之前的文章:C语言初阶:六.算数操作_如何用编程表示除法-CSDN博客 C语言操作符是用于执行各种运算和操作的符号。包括算术操作符(如、-、*、/、%)&#…...
)
GO excelize 读取excel进行时间类型转换(自动转换)
GO excelize 读取excel进行时间类型转换(自动转换) 需求分析 需求:如何自动识别excel中的时间类型数据并转化成对应的 "Y-m-d H:i:s"类型数据。 分析:excelize在读取excel时,GetRows() 返回的都是字符串类…...

【算法与数据结构】二分查找思想
#1024程序员节|征文# 正文: 二分查找(binary search)是一种基于分治策略的高效搜索算法。它利用数据的有序性,每轮缩小一半搜索范围,直至找到目标元素或搜索区间为空为止,其实有时候数据没有序…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...
