【C++篇】栈的层叠与队列的流动:在 STL 的韵律中探寻数据结构的优雅之舞

文章目录
- C++ 栈与队列详解:基础与进阶应用
- 前言
- 第一章:栈的介绍与使用
- 1.1 栈的介绍
- 1.2 栈的使用
- 1.2.1 最小栈
- 1.2.2 示例与输出
- 1.3 栈的模拟实现
- 第二章:队列的介绍与使用
- 2.1 队列的介绍
- 2.2 队列的使用
- 2.2.1 示例与输出
- 2.3 队列的模拟实现
- 2.3.1 示例与输出
- 第三章:优先队列的介绍与使用
- 3.1 优先队列的介绍
- 3.2 优先队列的使用
- 3.2.1 示例:默认大顶堆
- 3.2.2 示例与输出
- 3.2.3 示例:小顶堆
- 3.3 优先队列的模拟实现
- 3.3.1 示例与输出
- 第四章:容器适配器
- 4.1 什么是容器适配器
- 4.2 deque 的简单介绍
- 4.2.1 deque 的原理介绍
- 4.2.2 deque 的缺陷
- 4.2.3 deque 的常见操作
- 4.3 为什么选择 deque 作为 stack 和 queue 的底层默认容器
- 4.4 STL 标准库中 stack 和 queue 的模拟实现
- 4.4.1 stack 的模拟实现
- 4.4.2 queue 的模拟实现
- 第五章:总结
- 5.1 核心要点回顾
C++ 栈与队列详解:基础与进阶应用
💬 欢迎讨论:在学习过程中,如果有任何疑问或想法,欢迎在评论区留言一起讨论。
👍 点赞、收藏与分享:觉得这篇文章对你有帮助吗?记得点赞、收藏并分享给更多的朋友吧!你们的支持是我不断进步的动力!
🚀 分享给更多人:如果你觉得这篇文章对你有帮助,欢迎分享给更多对 C++ 感兴趣的朋友,一起学习进步!
前言
栈与队列是常见的数据结构,常被用于不同的算法场景。在本文中,我们将详细探讨栈与队列的基本概念、实际应用及其模拟实现。栈和队列在日常开发中的重要性不言而喻,通过对这两种数据结构的深入理解,将助你更加灵活地应对算法题目和工程开发。
在阅读本篇之前,可以先看看stl最基础的部分:
【C++篇】揭开 C++ STL list 容器的神秘面纱:从底层设计到高效应用的全景解析(附源码)
【C++篇】从零实现 C++ Vector:深度剖析 STL 的核心机制与优化
第一章:栈的介绍与使用
1.1 栈的介绍
栈 (Stack) 是一种 后进先出 (LIFO, Last In First Out) 的数据结构。这意味着栈中最后一个被插入的元素会第一个被移出。这种特性使得栈在实现某些算法时非常有用,例如函数调用栈、表达式求值以及括号匹配等。
栈提供的基本操作包括:
- push():将元素压入栈顶。
- pop():将栈顶元素弹出。
- top():获取栈顶元素。
- empty():检查栈是否为空。
- size():获取栈中元素的数量。
常见的栈使用场景有表达式求值、深度优先搜索(DFS)以及回溯法。
1.2 栈的使用
1.2.1 最小栈
最小栈 (Min Stack) 是栈的扩展应用,除了提供基本的栈操作外,还能够在常量时间内返回栈中的最小值。下面展示一个最小栈的具体实现。
#include <stack>
using namespace std;class MinStack {
public:// 构造函数MinStack() {}// 将元素 x 压入栈中void push(int x) { _elem.push(x); // 元素入栈if (_min.empty() || x <= _min.top()) { _min.push(x); // 如果 x 小于等于当前最小值,则将 x 也压入 _min 栈}}// 移除栈顶元素void pop() {if (_min.top() == _elem.top()) {_min.pop(); // 如果当前栈顶元素是最小值,将其从 _min 栈中移除}_elem.pop();}// 获取栈顶元素int top() { return _elem.top(); }// 获取当前栈中的最小值int getMin() { return _min.top(); }private:stack<int> _elem; // 存储栈中的所有元素stack<int> _min; // 存储栈中的最小值
};
1.2.2 示例与输出
int main() {MinStack minStack;minStack.push(-2);minStack.push(0);minStack.push(-3);cout << "Current Min: " << minStack.getMin() << endl; // 输出 -3minStack.pop();cout << "Top: " << minStack.top() << endl; // 输出 0cout << "Current Min: " << minStack.getMin() << endl; // 输出 -2return 0;
}
输出结果:
Current Min: -3
Top: 0
Current Min: -2
在这个例子中,我们实现了一个最小栈,可以在常量时间内获取栈中的最小值。在压栈和弹栈操作时,我们同步更新 _min 栈以维护最小值。
1.3 栈的模拟实现
栈的标准实现使用
std::stack容器,但在某些场景下,可以使用std::vector来模拟栈的功能。由于栈的所有操作都围绕末端进行,因此vector的尾插操作与stack类似。
#include <vector>
using namespace std;template <typename T>
class SimulatedStack {
public:// 向栈中压入元素void push(const T& x) {_data.push_back(x);}// 弹出栈顶元素void pop() {_data.pop_back();}// 获取栈顶元素T& top() {return _data.back();}// 检查栈是否为空bool empty() const {return _data.empty();}// 获取栈的大小size_t size() const {return _data.size();}private:vector<T> _data; // 用于存储栈元素的容器
};
这种模拟实现使用了 vector 的尾插操作,可以高效地模拟栈的行为。
第二章:队列的介绍与使用
2.1 队列的介绍
队列 (Queue) 是一种 先进先出 (FIFO, First In First Out) 的数据结构。这意味着第一个进入队列的元素会第一个被移出。队列通常用于任务调度、广度优先搜索 (BFS) 等场景。
队列的基本操作包括:
- push():将元素插入队尾。
- pop():移除队头元素。
- front():获取队头元素。
- back():获取队尾元素。
- empty():检查队列是否为空。
- size():获取队列中的元素数量。
2.2 队列的使用
以下是队列的基本用法展示,包括插入和删除元素。
#include <queue>
#include <iostream>
using namespace std;int main() {queue<int> q;q.push(1); // 向队尾插入元素1q.push(2); // 向队尾插入元素2cout << "Front: " << q.front() << endl; // 输出队头元素 1cout << "Back: " << q.back() << endl; // 输出队尾元素 2q.pop(); // 移除队头元素cout << "After pop, Front: " << q.front() << endl; // 输出新的队头元素 2return 0;
}
2.2.1 示例与输出
输出结果:
Front: 1
Back: 2
After pop, Front: 2
在这个例子中,我们展示了队列的 push()、pop()、front() 和 back() 操作。
2.3 队列的模拟实现
在一些场景中,标准库中的
std::queue可能无法满足特定需求,我们可以通过其他容器类来模拟实现队列。由于队列需要支持在头部删除和尾部插入的操作,使用std::list会比std::vector更为高效。list允许在常数时间内进行头部和尾部的插入与删除操作,因此非常适合用于队列的实现。
下面是一个基于 list 的队列模拟实现:
#include <list>
using namespace std;template <typename T>
class SimulatedQueue {
public:// 向队尾插入元素void push(const T& x) {_data.push_back(x);}// 移除队头元素void pop() {_data.pop_front();}// 获取队头元素T& front() {return _data.front();}// 获取队尾元素T& back() {return _data.back();}// 检查队列是否为空bool empty() const {return _data.empty();}// 获取队列的大小size_t size() const {return _data.size();}private:list<T> _data; // 用于存储队列元素的容器
};
2.3.1 示例与输出
int main() {SimulatedQueue<int> q;q.push(10); // 向队尾插入元素q.push(20);cout << "队头: " << q.front() << endl; // 输出队头元素 10cout << "队尾: " << q.back() << endl; // 输出队尾元素 20q.pop(); // 移除队头元素cout << "新的队头: " << q.front() << endl; // 输出新的队头元素 20return 0;
}
输出结果:
队头: 10
队尾: 20
新的队头: 20
在这个例子中,SimulatedQueue 模拟了队列的基本功能,包括在队尾插入元素和移除队头元素。
第三章:优先队列的介绍与使用
3.1 优先队列的介绍
优先队列 (Priority Queue) 是一种特殊类型的队列,其中每个元素都关联有一个优先级。优先队列的特点是元素的弹出顺序不再是按照先进先出,而是按照元素的优先级来决定。通常优先队列可以用来模拟堆结构。
在默认情况下,C++ 标准库中的 std::priority_queue 是一个大顶堆,即优先队列中的最大元素会优先弹出。我们也可以通过自定义比较函数来实现小顶堆,从而使得最小元素优先弹出。
优先队列的常见操作包括:
- push():向优先队列中插入元素。
- pop():移除优先级最高的元素。
- top():获取优先级最高的元素。
- empty():检查优先队列是否为空。
- size():获取优先队列中的元素数量。
3.2 优先队列的使用
下面展示了如何使用 std::priority_queue 进行优先队列操作。
3.2.1 示例:默认大顶堆
#include <iostream>
#include <queue>
#include <vector>
using namespace std;int main() {priority_queue<int> pq; // 默认大顶堆pq.push(10);pq.push(5);pq.push(20);cout << "优先级最高的元素: " << pq.top() << endl; // 输出 20pq.pop(); // 移除优先级最高的元素cout << "新的优先级最高的元素: " << pq.top() << endl; // 输出 10return 0;
}
3.2.2 示例与输出
输出结果:
优先级最高的元素: 20
新的优先级最高的元素: 10
在这个例子中,priority_queue<int> 实现了一个大顶堆,插入元素后,优先级最高的元素(值最大的元素)会优先弹出。
3.2.3 示例:小顶堆
我们也可以使用 std::greater<T> 来改变默认的比较方式,从而实现小顶堆。下面是一个小顶堆的例子:
#include <iostream>
#include <queue>
#include <vector>
using namespace std;int main() {priority_queue<int, vector<int>, greater<int>> pq; // 小顶堆pq.push(10);pq.push(5);pq.push(20);cout << "优先级最高的元素(最小值): " << pq.top() << endl; // 输出 5pq.pop(); // 移除优先级最高的元素cout << "新的优先级最高的元素: " << pq.top() << endl; // 输出 10return 0;
}
输出结果:
优先级最高的元素(最小值): 5
新的优先级最高的元素: 10
在这个例子中,priority_queue<int, vector<int>, greater<int>> 实现了一个小顶堆,其中优先级最高的元素是值最小的元素。
3.3 优先队列的模拟实现
优先队列通常是基于堆实现的。在 C++ 中,标准库中的
priority_queue使用std::vector作为底层存储,并通过堆算法管理优先级。在需要自定义优先队列行为时,可以自己实现一个简单的优先队列,利用堆的概念来操作。
下面是一个基于 std::vector 实现的简单优先队列:
#pragma once#include <iostream>
#include <vector>
using namespace std;// priority_queue--->堆
namespace W {// 默认的比较函数为 less,实现大顶堆template<class T>struct less {bool operator()(const T& left, const T& right) {return left < right;}};// greater 实现小顶堆template<class T>struct greater {bool operator()(const T& left, const T& right) {return left > right;}};template<class T, class Container = std::vector<T>, class Compare = less<T>>class priority_queue {public:// 创造空的优先级队列priority_queue() : c() {}// 构造函数支持从迭代器范围初始化template<class Iterator>priority_queue(Iterator first, Iterator last): c(first, last) {// 将 c 中的元素调整成堆的结构int count = c.size();int root = ((count - 2) >> 1);for (; root >= 0; root--)AdjustDown(root);}// 向队列中插入元素void push(const T& data) {c.push_back(data);AdjustUP(c.size() - 1);}// 移除优先级最高的元素void pop() {if (empty())return;swap(c.front(), c.back());c.pop_back();AdjustDown(0);}// 获取优先队列的大小size_t size() const {return c.size();}// 检查优先队列是否为空bool empty() const {return c.empty();}// 返回优先级最高的元素(不允许修改)const T& top() const {return c.front();}private:// 向上调整,维护堆的性质void AdjustUP(int child) {// 计算父节点的索引,等同于 (child - 1) / 2,移位操作符效率更快int parent = ((child - 1) >> 1);while (child) {if (Compare()(c[parent], c[child])) {swap(c[child], c[parent]);child = parent;parent = ((child - 1) >> 1);} else {return;}}}// 向下调整,维护堆的性质void AdjustDown(int parent) {size_t child = parent * 2 + 1;while (child < c.size()) {// 找到父节点较大的孩子if (child + 1 < c.size() && Compare()(c[child], c[child + 1])) {child += 1;}// 检查双亲是否满足堆的条件if (Compare()(c[parent], c[child])) {swap(c[child], c[parent]);parent = child;child = parent * 2 + 1;} else {return;}}}private:Container c; // 底层容器,默认为 vector};
}3.3.1 示例与输出
void TestQueuePriority() {W::priority_queue<int> q1;// 向大顶堆中插入元素q1.push(5);q1.push(1);q1.push(4);q1.push(2);q1.push(3);q1.push(6);// 输出堆顶元素cout << "优先级最高的元素: " << q1.top() << endl; // 输出 6// 弹出两个元素q1.pop();q1.pop();// 再次输出堆顶元素cout << "新的优先级最高的元素: " << q1.top() << endl; // 输出 4// 使用 greater 创建小顶堆vector<int> v{5, 1, 4, 2, 3, 6};W::priority_queue<int, vector<int>, W::greater<int>> q2(v.begin(), v.end());// 输出小顶堆的堆顶元素cout << "优先级最高的元素(最小值): " << q2.top() << endl; // 输出 1// 弹出两个元素q2.pop();q2.pop();// 再次输出小顶堆的堆顶元素cout << "新的优先级最高的元素(最小值): " << q2.top() << endl; // 输出 3
}
输出结果:
优先级最高的元素: 6
新的优先级最高的元素: 4
优先级最高的元素(最小值): 1
新的优先级最高的元素(最小值): 3
在这个模拟实现中,我们使用 std::vector 作为底层容器,并且通过堆排序算法来维护优先队列的顺序。通过 less 和 greater 函数对象,我们可以分别实现大顶堆和小顶堆。
第四章:容器适配器
4.1 什么是容器适配器
容器适配器 (Container Adapter) 是一种设计模式,目的是将一种容器包装为另一种接口形式。容器适配器提供了一组特定的成员函数来访问底层的容器。C++ 标准库中,
stack、queue和priority_queue都是容器适配器,它们对容器的操作进行了限制,并定义了特定的访问规则。

容器适配器本质上是对基础容器的封装,它们可以使用
vector、deque、list等作为底层实现,而具体使用哪种容器可以根据需求进行调整。容器适配器只暴露了某些特定的操作,而底层容器的更多操作则被隐藏。
虽然stack和queue中也可以存放元素,但在STL中并没有将其划分在容器的行列,而是将其称为容器适配器,这是因为stack和队列只是对其他容器的接口进行了包装,STL中stack和queue默认使用deque
常见的容器适配器:
-
stack:实现后进先出(LIFO)原则。

-
queue:实现先进先出(FIFO)原则。

- priority_queue:基于优先级进行元素的弹出,通常是大顶堆。

4.2 deque 的简单介绍
双端队列 (deque, Double-Ended Queue) 是一种可以在头尾两端进行高效插入和删除操作的序列式容器。与 vector 类似,deque 提供了动态数组的功能,但它比 vector 更加灵活,允许在头尾两端都进行元素的添加和删除。

4.2.1 deque 的原理介绍
- 双端操作:
deque提供了双端操作,即允许在容器的两端进行插入和删除操作。其时间复杂度为常数时间 O ( 1 ) O(1) O(1),这使得它比vector更适合需要频繁在两端插入或删除元素的场景。 - 非连续存储:虽然
deque表面上看起来像是一个连续的数组,但它的底层实现并非真正连续,而是由多块小的连续内存块组合而成,这就允许deque在进行元素插入或删除时,不需要像vector一样移动大量元素。
下面是一张简化的 deque 的内存布局示意图:
--------------------------------
| Block 1 | Block 2 | Block 3 |
--------------------------------
每个块表示 deque 底层的一部分内存,插入或删除元素时,只需要操作相应块中的数据,而不需要重新分配整个数组的内存。

双端队列底层是一段假象的连续空间,实际是分段连续的,为了维护其“整体连续”以及随机访问
的假象,落在了deque的迭代器身上,因此deque的迭代器设计就比较复杂,如下图所示:

那deque是如何借助其迭代器维护其假想连续的结构呢?

了解一下即可
4.2.2 deque 的缺陷
虽然 deque 在插入和删除操作上比 vector 更高效,但它也有一些缺点:
- 遍历性能较低:由于
deque的存储结构不是一个连续的内存块,所以在遍历deque时,迭代器需要处理内存块之间的跳转,导致遍历性能不如vector。 - 内存利用率稍低:因为
deque是由多个小内存块组成的,所以它的内存利用率相比vector稍差。不过与list比较,deque的内存效率还是更高。
4.2.3 deque 的常见操作
#include <deque>
#include <iostream>
using namespace std;int main() {deque<int> d;// 在队列的两端插入元素d.push_back(10);d.push_back(20);d.push_front(5);cout << "队头: " << d.front() << endl; // 输出 5cout << "队尾: " << d.back() << endl; // 输出 20// 删除队列的两端元素d.pop_front();d.pop_back();cout << "新的队头: " << d.front() << endl; // 输出 10return 0;
}
输出结果:
队头: 5
队尾: 20
新的队头: 10
这个示例展示了 deque 如何进行两端的插入和删除操作。可以看到,deque 支持同时在队头和队尾进行高效的操作。
4.3 为什么选择 deque 作为 stack 和 queue 的底层默认容器
C++ 标准库中,stack 和 queue 的底层容器默认使用 deque,这是因为 deque 在元素插入和删除时的性能优势以及空间利用率较高的特点,正好符合 stack 和 queue 对容器的需求。
- 高效的尾部插入和删除:对于
stack,只需要支持在容器的尾部插入和删除元素,deque的push_back()和pop_back()操作可以在常数时间内完成,比vector在扩容时效率更高。 - 高效的头部插入和删除:对于
queue,需要在尾部插入元素、在头部删除元素,deque同时支持push_back()和pop_front()操作,效率比list高,且不需要存储额外的指针信息。
虽然 vector 也可以作为 stack 的底层容器,但它在尾部插入元素时需要在扩容时移动大量元素,因此效率不如 deque。而 list 虽然也支持两端插入删除操作,但由于需要存储额外的指针信息,空间利用率不如 deque 高。因此,deque 被认为是 stack 和 queue 的默认最佳选择。
4.4 STL 标准库中 stack 和 queue 的模拟实现
4.4.1 stack 的模拟实现
stack 的模拟实现只需要封装一个可以支持末端插入和删除操作的容器,默认情况下,使用 deque 作为底层容器。
#include <deque>namespace W {template <typename T, typename Container = deque<T>>
class stack {
public:stack() {}// 向栈中压入元素void push(const T& x) {_c.push_back(x);}// 弹出栈顶元素void pop() {_c.pop_back();}// 获取栈顶元素T& top() {return _c.back();}// 检查栈是否为空bool empty() const {return _c.empty();}// 获取栈的大小size_t size() const {return _c.size();}private:Container _c; // 底层容器,默认使用 deque
};
}
4.4.2 queue 的模拟实现
queue 的实现需要支持队尾插入元素、队头删除元素的操作。类似 stack,queue 默认使用 deque 作为底层容器。
#include <deque>namespace W {template <typename T, typename Container = deque<T>>
class queue {
public:queue() {}// 向队尾插入元素void push(const T& x) {_c.push_back(x);}// 移除队头元素void pop() {_c.pop_front();}// 获取队头元素T& front() {return _c.front();}// 获取队尾元素T& back() {return _c.back();}// 检查队列是否为空bool empty() const {return _c.empty();}// 获取队列的大小size_t size() const {return _c.size();}private:Container _c; // 底层容器,默认使用 deque
};
}
第五章:总结
在本文中,我们详细探讨了 栈 (stack) 和 队列 (queue) 的概念、应用及其实现方式。通过对 deque 和 priority _queue 的深入理解,我们可以更高效地解决实际编程问题。
5.1 核心要点回顾
- 栈是一种后进先出的数据结构,常用于表达式求值、函数调用栈等。
- 队列是一种先进先出的数据结构,广泛应用于任务调度、广度优先搜索等场景。
- 优先队列根据元素的优先级进行排序,常用于调度和路径优化算法。
deque作为双端队列,支持在头尾两端进行高效的插入和删除操作。- 容器适配器
stack和queue使用deque作为底层容器,利用其高效的插入删除操作实现栈和队列的功能。
通过对这些数据结构的深入理解,我们能够在编程中更加灵活、准确地选择合适的工具来解决实际问题。
💬 讨论区:如果你有任何问题,欢迎在评论区留言讨论!
👍 支持一下:如果你觉得这篇文章对你有帮助,请点赞、收藏并分享给更多学习者!
以上就是关于【C++篇】栈的层叠与队列的流动:在 STL 的韵律中探寻数据结构的优雅之舞的内容啦,各位大佬有什么问题欢迎在评论区指正,或者私信我也是可以的啦,您的支持是我创作的最大动力!❤️

相关文章:

【C++篇】栈的层叠与队列的流动:在 STL 的韵律中探寻数据结构的优雅之舞
文章目录 C 栈与队列详解:基础与进阶应用前言第一章:栈的介绍与使用1.1 栈的介绍1.2 栈的使用1.2.1 最小栈1.2.2 示例与输出 1.3 栈的模拟实现 第二章:队列的介绍与使用2.1 队列的介绍2.2 队列的使用2.2.1 示例与输出 2.3 队列的模拟实现2.3.…...

使用 Flask 实现简单的登录注册功能
目录 1. 引言 2. 环境准备 3. 数据库设置 4. Flask 应用基本配置 5. 实现用户注册 6. 实现用户登录 7. 路由配置 8. 创建前端页面 9. 结论 1. 引言 在这篇文章中,我们将使用 Flask 框架创建一个简单的登录和注册系统。Flask 是一个轻量级的 Python Web 框架…...

计算机毕业设计Python+大模型微博情感分析 微博舆情预测 微博爬虫 微博大数据 舆情分析系统 大数据毕业设计 NLP文本分类 机器学习 深度学习 AI
温馨提示:文末有 CSDN 平台官方提供的学长联系方式的名片! 温馨提示:文末有 CSDN 平台官方提供的学长联系方式的名片! 温馨提示:文末有 CSDN 平台官方提供的学长联系方式的名片! 《Python大模型微博情感分析…...

CTF--Misc题型小结
(萌新笔记,多多关照,不足之处请及时提出。) 不定时更新~ 目录 密码学相关 文件类型判断 file命令 文件头类型 strings读取 隐写术 尺寸修改 文件头等缺失 EXIF隐写 thumbnail 隐写 文件分离&提取 binwalk foremo…...

深度学习系列——RNN/LSTM/GRU,seq2seq/attention机制
1、RNN/LSTM/GRU可参考: https://zhuanlan.zhihu.com/p/636756912 (1)对于这里面RNN的表示中,使用了输入x和h的拼接描述,其他公式中也是如此 (2)各符号图含义如下 2、关于RNN细节,…...

通过call指令来学习指令摘要表的细节
E8 cw cw 表示E8后面跟随2 字节 (什么数不知道) rel16 指在与指令同一代码段内的相对地址偏移 D ,指向Instruction Operand Encoding 表中的D列, 他告诉我们 操作数1 是一个0FFSET N.S. 在64位模式下,某些指令需要使用“地址覆盖前缀”(address over…...

10分钟使用Strapi(无头CMS)生成基于Node.js的API接口,告别繁琐开发,保姆级教程,持续更新中。
一、什么是Strapi? Strapi 是一个开源的无头(headless) CMS,开发者可以自由选择他们喜欢的开发工具和框架,内容编辑人员使用自有的应用程序来管理和分发他们的内容。得益于插件系统,Strapi 是一个灵活的 C…...

创建插件 DLL 项目
Step 1: 创建插件 DLL 项目 在 Visual Studio 中创建一个新的 DLL 项目,并添加以下文件和代码。 头文件:CShapeBase.h cpp 复制代码 #pragma once #include <afxwin.h> // MFC 必需头文件 #include <string> #include <vector> #i…...

OpenCV双目相机外参标定C++
基于OpenCV库实现双目测量系统外参标定过程。通过分析双目测量系统左右相机拍摄的棋盘格标定板图像,包括角点检测、立体标定、立体校正和畸变校正的步骤,获取左右相机的相对位置关系和姿态。 a.检测每张图像中的棋盘格角点,并进行亚像素级精…...
【GESP】C++一级练习BCQM3055,4位数间隔输出
一级知识点取余、整除运算和格式化输出知识点应用。其实也可以用string去处理,那就属于GESP三级的知识点范畴了,孩子暂未涉及。 题目题解详见:https://www.coderli.com/gesp-1-bcqm3055/ https://www.coderli.com/gesp-1-bcqm3055/https://w…...

纯血鸿蒙的最难时刻才开始
关注卢松松,会经常给你分享一些我的经验和观点。 纯血鸿蒙(HarmonyOS NEXT)也正式发布了,绝对是一个历史性时刻,但最难的鸿蒙第二个阶段,也就是生态圈的建设,才刚刚开始。 目前,我劝你现在不要升级到鸿蒙…...

记一个mysql的坑
数据库表user, 存在一个name字段,字段为varchar类型 现在user表有这么两条记录: idnameageclass1NULL18一班2lisi20二班 假如我根据下面这一条件去更新,更新成功数据行显示为0 update user set age 19 where age 18 and class “一班”…...

Java中的设计模式:单例模式详解
摘要 单例模式(Singleton Pattern)是Java中最常用的设计模式之一,属于创建型模式。它的主要目的是确保一个类在系统中只有一个实例,并提供一个全局访问点来访问该实例。 1. 单例模式的定义 单例模式确保一个类只有一个实例&…...

NanoTrack原理与转tensorrt推理
文章目录 前言一、NanoTrack 工作原理二、运行demo与转换tensorrt模型2.1 运行pt模型demo2.2 转onnx模型2.3 转tensorrt模型2.4 运行trt模型推理 三、推理速度对比总结 前言 NanoTrack 是一种轻量级且高效的目标跟踪算法,基于Siamese网络架构,旨在在资源…...

YOLO11改进 | 卷积模块 | 卷积模块替换为选择性内核SKConv【附完整代码一键运行】
秋招面试专栏推荐 :深度学习算法工程师面试问题总结【百面算法工程师】——点击即可跳转 💡💡💡本专栏所有程序均经过测试,可成功执行💡💡💡 本文给大家带来的教程是将YOLO11的卷积替…...

CentOS进入单用户模式进行密码重置
一、单用户模式介绍 单用户模式是一种特殊的启动模式,主要用于系统维护和故障排除。在单用户模式下,系统以最小化的状态启动,只有最基本的系统服务会被加载,通常只有root用户可以登录。这种模式提供了对系统的完全控制࿰…...

bitpoke- mysql-operator cluster
sidecar版本只支持到8.0.35,35可以支持到mysql8.0.35 . 默认镜像是5.7的。需要自己打sidecar的镜像: # Docker image for sidecar containers # https://github.com/bitpoke/mysql-operator/tree/master/images/mysql-operator-sidecar-8.0 # 参考5…...

第5课 基本数据类型
一、数据类型的诞生 在Python的世界里,万物皆对象,每个对象都有自己的若干属性,每一个属性都能描述对象的某一个方面。就像我们每个人,都有自己的身高、年龄、姓名、性别等很多方面的信息,这里的身高、年龄、姓名、性…...
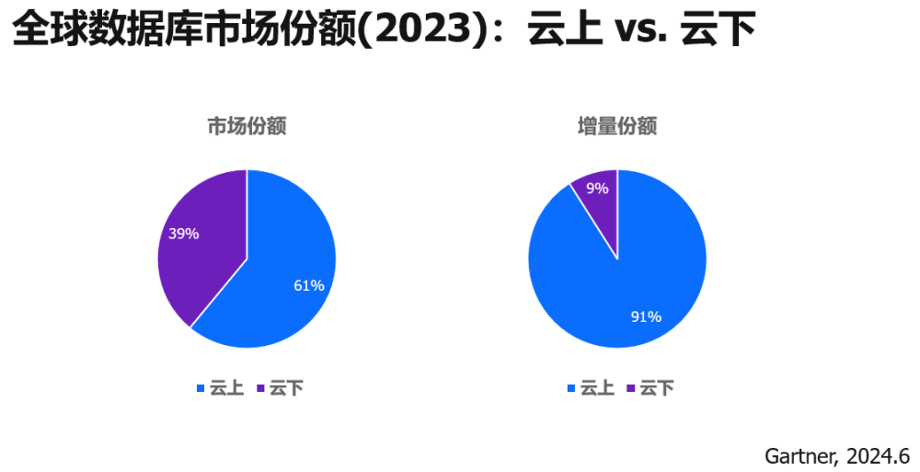
OceanBase 首席科学家阳振坤:大模型时代的数据库思考
2024年 OceanBase 年度大会 即将于10月23日,在北京举行。 欢迎到现场了解更多“SQL AI ” 的探讨与分享! 近期,2024年金融业数据库技术大会在北京圆满举行,聚焦“大模型时代下数据库的创新发展”议题,汇聚了国内外众多…...

国内知名的几个镜像源
在国内,有许多常用的Python库镜像源可以帮助加速库的下载。以下是几个知名的镜像源: 1. 清华大学TUNA协会 网址: https://pypi.tuna.tsinghua.edu.cn/simple命令示例:pip install numpy --index-url https://pypi.tuna.tsinghua.edu.cn/simple2. 阿里云…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...
