当前位置：首页 > news >正文

算法设计与分析——动态规划

news 2025/7/5 3:39:32

1.动态规划基础

1.1动态规划的基本思想

动态规划建立在最优原则的基础上，在每一步决策上列出可能的局部解，按某些条件舍弃不能得到最优解的局部解，通过逐层筛选减少计算量。每一步都经过筛选，以每一步的最优性来保证全局的最优性。具体来说，动态规划算法仍然是将待求解的问题的若干子问题，采用列表技术，将从小到大的子问题的计算答案存储于一张表中，由于将原问题分解后的各个子问题可能存在重复，所以当重复遇到该子问题时，只需要查表继续问题的求解，而不需要重复计算。所以动态规划算法的基本思想是记录子问题并不断填表。

1.2动态规划的基本要素

通常一个可以用动态规划算法求解的问题应该具有3个要素：最优子结构、无后效性和子问题重叠性。

最优子结构：动态规划算法的关键在于正确的找出基本的递推关系式和恰当的边界条件。要做到这一点，必须将原问题分解为几个相互联系的阶段，在每一个子问题的求解中，均利用它前面子问题的最优化结果，依次进行，最有一个子问题所得的最优解就是整个问题的最优解。

无后效性：将各个阶段依次排好之后，一旦某阶段的状态已经确定，它以前各阶段的状态无法直接影响未来的决策，并且当前状态的决策只是对以往决策的总结。

子问题重叠性：动态规划计算最优值时，每次计算所产生的子问题并不总是新问题，有些问题被重复计算多次，但是动态规划将这些子问题的解存放在表格中，不需要重复计算，提高了程序的效率。

1.3动态规划的基本方法

动态规划问题千奇百怪，有诸多变种，但是动态规划具有比较鲜明的特征，即最优子结构和重叠子问题。解决动态规划问题的思路很重要，掌握下面五步之后再加以练习能够解决许多动态规划问题。

确定dp的含义：dp数组中存放的是每个子问题的最优解。
推导动态转移方程：在动态规划问题中
dp的初始化
遍历顺序
打印表格

2.矩阵连乘问题

给定 $n$ 个矩阵 $\left \{ {A_{1},A_{2},...,A_{n}} \right \}$ ，其中矩阵 $A_{i}$ 的维数为 $p_{i-1}$ × $p_{i}$ ，且 $A_{i}$ 与 $A_{i+1}$ 是可乘的，考察这 $n$ 个矩阵的连乘积 $A_{1}A_{2}...A{n}$ 。由于矩阵乘法满足结合律，所以计算矩阵的连乘可以有许多不同的计算次序，这种计算次序可以用加括号的方式来确定。如何确定计算矩阵连乘积的计算次序，使得依此次序计算矩阵连乘积需要的数乘次数最少？

设有四个矩阵A、B、C、D，它们的维数分别是：50×10，10×40，40×30，30×5，其完全加括号方式为：(A((BC)D))，(A(B(CD)))，((AB)(CD))，(((AB)C)D)，((A(BC))D)所需的乘法次数分别为16000，10500，36000，87500，34500。

对于 $n$ 个矩阵的连乘积，设其不同的计算次序为 $p(n)$ 。每种加括号方式都可以分解为两个矩阵的加括号方式： $(A_{1}...A_{k})(A_{k+1}...A_{n})$ ，其递推式为：

$p(n)=\sum_{k=1}^{n-1}p(k)p(n-k)$

卡特兰数是组合数学中一个常出现在各种计数问题中的数列。其递推式如下：

$h(n)=\sum_{k=0}^{n-1}h(k)h(n-k-1)$

该递推关系的解为： $C_{n}=\frac{(2n)!}{(n+1)!n!}$ 。

卡特兰数的渐近增长为 $C_{n}$ ~ $\frac{4^{n}}{n^{3/2}\sqrt{\pi }}$

2.1分析最优子结构

设 $n$ 个矩阵连乘的最佳计算次序为 $(A_{1}...A_{k})(A_{k+1}...A_{n})$ ，则 $(A_{1}...A_{k})$ 与 $(A_{k+1}...A_{n})$ 连乘的计算次序都是最优的。矩阵连乘计算次序问题的最优解包含着子问题的最优解。这种性质称为最优子结构性质，问题的最优子结构性质是该问题可用DP方法求解的显著特征。

2.2递归关系建立

将矩阵连乘积 $(A_{i}A_{i+1}...A_{j})$ 记为 $A[i:j]$ ，这里 $i\leqslant j$ 。 $A[i:j]$ 的总计算量为： $A[i:k]$ 的计算量加上 $A[k+1:j]$ 的计算量，再加上 $A[i:k]$ 和 $A[k+1:j]$ 相乘的计算量。

设计算 $A[i:j]$ 的最佳计算次序所对应的乘法次数为 $m[i:j]$ ，则原问题的最优解为 $m[1:n]$

当 $i=j$ 时， $A[i:j]=A_i$ ,因此 $m_i=0,i=1,2,...,n$

当 $i<j$ 时， $m[i,j]=min_{i\leqslant k\leqslant j}(m[i,k]+m[k+1,j] + p_{i-1}p_{k}p_{j})$

2.3代码分析

#include<stdio.h>
#define N 7
void MatrixChain(int *p,int n,int m[][N],int s[][N])
{for(int i = 0; i <= n; ++i) m[i][i] = 0;//自乘的消耗为0for(int r = 2; r <= n; ++r){for(int i = 1; i <= n - r + 1; ++i){int j = i + r - 1;m[i][j] = m[i+1][j] + p[i-1]*p[i]*p[j];//试探性的赋值。s[i][j] = i;for(int k = i + 1; k < j; ++k){int t = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j];if(t < m[i][j]){m[i][j] = t;      s[i][j] = k;}}}}
}void Traceback(int i, int j, int s[][N]){if(i == j) printf("A%d",i);else{printf("(");Traceback(i,s[i][j],s);Traceback(s[i][j]+1,j,s);printf(")");}
}      int main()
{int p[N]={30,35,15,5,10,20,24};int m[N][N],s[N][N];MatrixChain(p,N-1,m,s);printf("矩阵的最佳乘积方式为：");Traceback(1,6,s);return 0;
}

3.电路布线问题

在一块电路板的上、下两端分别有 $n$ 个接线柱。根据电路设计，要求用导线 $(i,\pi (i))$ 将上端接线柱与下端接线柱相连，如图所示：

其中 $\pi(i)$ 是 $\{1,2,...,n\}$ 的一个排列，导线 $(i,\pi (i))$ 称为该电路的第 $i$ 条连线。对于任何 $1\leqslant i< j\leqslant n$ ，第 $i$ 条连线和第 $j$ 条连线相交的充分且必要条件是 $\pi(i)>\pi(j)$ 。

在制作电路板时，要求将这 $n$ 条连线分布到若干绝缘层上。在同一层上的连线不可相交。电路布线问题要确定将那些连线安排在第一层上，使得该层上要有尽可能多的连线。换句话说，该问题要确定导线集 $Nets$ 的最大不相交子集。

3.1最优子结构分析

记 $N(i,j)=\{t|(t,\pi (t))\in Nets,t\leqslant i,\pi (t)\leqslant j \}$ 。 $N(i,j)$ 的最大不相交子集为 $MNS(i,j)$ 。 $Size(i,j)=|MNS(i,j)|$ 。

（1）当 $i=1$ 时， $MNS(1,j)=N(1,j)=\{(1,\pi(1))\}$ 。

（2）当 $i>1$ 时，

若 $j<\pi(i)$ 。此时， $(i,\pi(i)\nsubseteq N(i,j))$ 。所以 $N(i,j) = N(i-1,j)$ ，从而 $Size(i,j)=Size(i-1,j)$ 。

若 $j\geq \pi(i)$ 。此时，

如果 $(i,\pi(i)\in MNS(i,j))$ ，则对任意的 $(t,\pi(t)\in \in MNS(i,j))$ 有 $t<i$ 且 $\pi(t)<\pi(i)$ 。在这种情况下 $MNS(i,j)-\{(i,\pi(i))\}$ 是 $N(i-1,\pi(i)-1)$ 的最大不相交子集，从而 $Size(i,j)=Size(i-1,\pi(i)-1)+1$ 。

如果 $(i,\pi(i)\nsubseteq MNS(i,j))$ ，则对任意的 $(t,\pi(t)\in \in MNS(i,j))$ ，有 $t<i$ 。从而 $MNS(i-1,j)\subseteq N(i,j)$ 。因此， $Size(i,j)\geqslant Size(i-1,j)$ 。另一方面有 $MNS(i,j)\subseteq N(i-1,j)$ ，因此又有 $Size(i,j)\leqslant Size(i-1,j)$ ，从而有 $Size(i,j)= Size(i-1,j)$ 。

3.2递归关系建立

（1）当 $i=1$ 时， $Size(1,j)=\left\{\begin{matrix} 0~~~~~ j<\pi(1) & \\ 1~~~~~ j \geqslant\pi(1)& \end{matrix}\right.$

（2）当 $i>1$ 时，

$Size(i,j)=\left\{\begin{matrix} Size(i-1,j) ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~j< \pi(i)& \\ max\{Size(i-1,j),Size(i-1,\pi(i)-1)+1\}~~~~~j\geqslant \pi(i)& \end{matrix}\right.$

电路布线问题的最优值为 $Size(n,n)$ 。

3.3代码分析

void MNS(int C[],int n,int **size)
{for(int j = 0; j < C[1];++j) size[1][j] = 0;for(int j = C[1]; j <= n;++j) size[1][j] = 1;for(int i = 2; i < n; ++i){for(int j = 1; j < C[i]; ++j)    size[i][j] = size[i-1][j];for(int j = C[i]; j <= n; ++j)    size[i][j] = max(size[i-1][j],size[i-1][C[i]-1]+1);}size[n][n] = max(size[n-1][n],size[n-1][C[n]-1]+1);
}

4.最长公共子序列

若给定子序列 $X=\{x_{1},x_{2},...,x_{m}\}$ ，则 $Z=\{z_{1},z_{2},...z_{k}\}$ 是X的子序列是指存在一个严格递增下标序列 $\{i_{1},i_{2},...i_{k}\}$ 使得对于所有的 $j=1,2,...,k$ 有 $z_{j}=x_{i_{j}}$ 。

给定两个序列 $X$ 和 $Y$ ，当另一序列 $Z$ 既是 $X$ 的子序列又是 $Y$ 的子序列时，称 $Z$ 是序列 $X$ 和 $Y$ 的公共子序列。我们的问题是给定两个序列 $X=\{x_{1},x_{2},...,x_{m}\}$ 和 $Y=\{y_{1},y_{2},...,y_{n}\}$ ，找出 $X$ 和 $Y$ 的最长公共子序列。

4.1最优子结构分析

设序列 $X=\{x_{1},x_{2},...,x_{m}\}$ 和 $Y=\{y_{1},y_{2},...,y_{n}\}$ 的最长公共子序列为 $Z_{k}=\{z_{1},z_{2},...z_{k}\}$ ，则

（1）若 $x_{m}=y_{n}$ ，则 $z_{k}=x_{m}=y_{n}$ ，且 $Z_{k-1}$ 是 $X_{m-1}$ 和 $Y_{n-1}$ 的最长公共子序列。

（2）若 $x_{m}\neq y_n$ 且 $z_k\neq x_m$ ，则 $Z_k$ 是 $X_{m-1}$ 和 $Y_n$ 的最长公共子序列。

（3）若 $x_{m}\neq y_n$ 且 $z_k\neq y_n$ ，则 $Z_k$ 是 $X_{m}$ 和 $Y_{n-1}$ 的最长公共子序列。

由此可见，两个序列的最长公共子序列包含了这两个序列的前缀的最长公共子序列。因此，最长公共子序列问题具有最优子结构性质。

4.2递归关系建立

设二维数组 $c[i][j]$ 记录序列 $X_i$ 和 $Y_j$ 的最长公共子序列的长度。其中 $X=\{x_{1},x_{2},...,x_{m}\}$ ； $Y=\{y_{1},y_{2},...,y_{n}\}$ 。当 $i=0$ 或 $j=0$ 时，空序列是它们的最长公共子序列，此时 $c[i][j]=0$ 其它情况下：

$c[i][j]=\left\{\begin{matrix} 0~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~i=0~or~j=0\\ c[i-1][j-1]+1~~~~~~~~~~~~~~~~~~i,j>0~and~x_i=y_j\\ max\{c[i][j-1],c[i-1][j]\}~~~~~~i,j>0~and~x_i\neq y_j\end{matrix}\right.$

4.3代码分析

void LCSLength()
{for(int i = 1; i <= m; ++i) c[i][0] = 0;//存放各个子问题的最优值for(int j = 1; j <= n; ++j) b[0][j] = 0;//存放各个子问题最优值的来源for(int i = 1; i < m; ++i){for(int j = 1; i <= n; ++j){if(x[i]==y[j]){c[i][j] = c[i-1][j-1] + 1;b[i][j] = 1;}else if(c[i-1][j] >= c[i][j-1]){c[i-1] = c[i-1][j];b[i][j] = 3;}else {c[i][j] = c[i][j-1];b[i][j] = 2;}}}
}

5.图像压缩问题

图像的变位压缩存储格式将所给的像素点序列 $\{p_1,p_2,...p_n\}$ , $0\leqslant p_i\leqslant 255$ 分割 $m$ 个连续段 $S_1,S_2,...,S_m$ 。第 $i$ 个像素段 $S_i$ $(1\leqslant i\leqslant m)$ 中，有 $l[i]$ 个像素，且该段中每个像素都只用 $b[i]$ 位表示。设 $t[i]=\sum_{k=1}^{i-1}l[k]$ ，则第 $i$ 个像素段 $S_i$ 为

$S_i=\{p_{t[i]+1},...,p_{t[i]+l[i]}\} ~~~1\leqslant i\leqslant m$

设 $h_i=[log(max(p_k)+1)]$ ，则 $h_i\leqslant b[i]\leqslant 8$ 。因此需要用3位表示 $b[i]$ ，如果限制 $1\leqslant l[i]\leqslant 255$ ，则需要用8位来表示 $b[i]$ 。因此第 $i$ 个像素段所需要的存储空间为 $l[i]*b[i]+11$ 位。按此格式存储像素序列 $\{p_1,p_2,...p_n\}$ ，则需要 $\sum_{i=1}^{m}l[i]*b[i]+11m$ 位的空间。

图像压缩问题要求确定像素序列 $\{p_1,p_2,...p_n\}$ 的最优分段，使得依此分段所需要的存储空间最少。每个分段的长度不超过255位。

5.1最优子结构分析

设 $l[i]$ 、 $b[i]$ $(1\leqslant i\leqslant m)$ 是 $\{p_1,p_2,...p_n\}$ 的最优分段。显而易见， $l[1]$ 、 $b[1]$ 是 $\{p_1,...p_{l[1]}\}$ 的最优分段。图像压缩问题满足最优子结构性质。

设 $s[i]$ ， $1\leqslant i\leqslant n$ ，是像素序列 $\{p_1,...,p_i\}$ 的最优分段所需的存储位数。

$s[i]=min\{s[i-k]+k*bmax(i-k+1,i)\}+11$

其中 $bmax(i,j)=log(max(p_k)+1)$ 。

5.2代码分析

void Compress(int n, int p[], int s[], int l[], int b[]) {const int Lmax = 256;const int header = 11;s[0] = 0;for (int i = 1; i <= n; i++) {b[i] = length(p[i]); // 计算像素点 p[i] 需要的存储位数int bmax = b[i];s[i] = s[i - 1] + bmax; // 赋初值l[i] = 1;for (int k = 2; k <= i && k <= Lmax; k++) {if (bmax < b[i - k + 1]) {bmax = b[i - k + 1];}if (s[i] > s[i - k] + k * bmax) {s[i] = s[i - k] + k * bmax;l[i] = k;}}s[i] += header; // 添加头部信息的开销}
}

6.凸多边形最优三角剖分

凸多边形：一个简单多边形及其内部构成一个闭凸集时，称该简单多边形为凸多边形，即凸多边形边界上或内部的任意两点所连成的直线段上所有点均在凸多边形的内部或边界上。

为方便描述，用多边形顶点的逆时针序列表示凸多边形，即 $p=\{v_0,v_1,...v_n\}$ ，表示具有 $n+1$ 条边的凸多边形。

若 $v_i$ 与 $v_j$ 是多边形上的不相邻的两个顶点，则线段 $v_iv_j$ 称为多边形的一条弦。弦将多边形分割成两个多边形 $\{v_i,v_{i+1},...v_j\}$ 和 $\{v_j,v_{j+1},...v_i\}$ 。

多边形的三角剖分是将多边形分割成互不相交的三角形的弦的集合T。

凸多边形的最优三角剖分：给定凸多边形P，以及定义在由多边形的边和弦组成的三角形上的权函数w，要求确定该凸多边形的三角剖分，使得该三角剖分中诸三角形上权之和为最小。

6.1最优子结构分析

假设存在一个凸多边形的最优剖分 $P$ ，它的一个子凸多边形 $Q$ 不是最优剖分。也就是说存在一个代价更小的三角剖分 $Q^{'}$ 。如果是这样的话，使用 $Q^{'}$ 替换 $Q$ ，在保证其它子三角剖分不变的情况下，会产生一个新的整体三角剖分 $P^{'}$ ，它的代价更小，则与 $P$ 是最优三角剖分的假设矛盾。所以，凸多边形的最优三角剖分具有最优子结构性。

6.2递归关系建立

定义 $t[i][j]$ ， $1\leqslant i\leqslant j\leqslant n$ 为凸子多边形 $\{v_{i-1},v_i,...,v_j\}$ 的最优三角剖分所对应的权函数值，取其最优值。为方便起见，退化的多边形 $\{v_{i-1},v_i\}$ 具有权值0。根据此定义，要凸多边形 $(n+1)$ P的最有权值为 $t[1][n]$ 。

$t[i][j]$ 的值可以利用最优子结构性质递归地计算。当 $j-i\geqslant > 1$ 时，凸子多边形至少有3个顶点。由最优子结构性质， $t[i][j]$ 的值应为 $t[i][k]+t[k+1][j]+v_{i-1}v_kv_j$ ， $v_{i-1}v_kv_j$ 代表该三角形的权值，其中 $(i\leqslant k \leqslant j-1)$ 。因此

$t[i][j]=\left\{\begin{matrix} 0~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~i=j\\ min\{t[i][k]+t[k+1][j]+w(v_{i-1}v_kv_j)\}~~~~~~i<j\end{matrix}\right.$

6.3代码分析

void MinWeightTriangulation(int *weights, int n) {int t[N][N] = {0}; // 用于存储子问题的最优解int s[N][N] = {0}; // 用于存储分割点// 初始化for (int i = 1; i < n; i++) {t[i][i] = 0;}// 动态规划计算for (int r = 2; r < n; r++) {for (int i = 1; i < n - r + 1; i++) {int j = i + r - 1;t[i][j] = t[i + 1][j] + get_weight(i - 1, i, j, weights);s[i][j] = i;// 尝试所有分割点for (int k = i + 1; k < j; k++) {int u = t[i][k] + t[k + 1][j] + get_weight(i - 1, k, j, weights);if (u < t[i][j]) {t[i][j] = u;s[i][j] = k;}}}}
}

7.0-1背包问题

给定 $n$ 个物品和1个背包。物品 $i$ 的重量是 $w_i$ ，其价值为 $v_i$ ，背包的容量为 $W$ 。如何选择装入背包的物品，使得装入背包中物品的总价值最大? 通常称物体不可分割的背包问题为0-1背包问题。

问题的形式化描述为，给定 $W>0$ ， $w_i>0$ ， $v_i>0$ ， $1\leqslant i\leqslant n$ ，要求找出 $n$ 元0-1向量 $(x_1,x_2,...,x_n)$ ，满足：

$max\sum_{i=1}^{n}v_ix_i$

$\left\{\begin{matrix} \sum_{i=1}^{n}w_ix_i\leqslant W\\ x_i\in \{0,1\},1\leqslant i\leqslant n \end{matrix}\right.$

7.1最优子结构性分析

假设 $(x_1,x_2,...,x_n)$ 是所给0-1背包问题的已给最优解，则 $(x_2,...,x_n)$ 是下面相应子问题的一个最优解：

$max\sum_{i=2}^{n}v_ix_i$

$\left\{\begin{matrix} \sum_{i=2}^{n}w_ix_i\leqslant W-w_1x_1\\ x_i\in \{0,1\},2\leqslant i\leqslant n \end{matrix}\right.$

7.2递归关系建立

令 $C[i][j]$ 表示子问题 $\left\{\begin{matrix} \sum_{k=1}^{i}w_kx_k\leqslant j\\ x_k\in \{0,1\} ~~~~~1\leqslant k\leqslant i \end{matrix}\right.$ 的最优解。 $C[i-1][j-w_ix_i]$ 表示该问题的子问题 $\left\{\begin{matrix} \sum_{k=1}^{i-1}w_kx_k\leqslant j-w_ix_i\\ x_k,x_k\in \{0,1\} ~~~~~1\leqslant k\leqslant i-1 \end{matrix}\right.$ 的最优解。

最优解的递归关系式为：

$C[i][0]=c[0][j]=0, ~~1\leqslant i\leqslant n,~~1\leqslant j\leqslant W$

$C[i][j]=\left\{\begin{matrix} C[i-1][j]~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~j<w_i\\ max\{C[i-1][j],C[i-1][j-w_i]+v_i\}~~~j\geqslant w_i \end{matrix}\right.$

7.3代码分析

void knapsack(int W, int* p, int *w, int size)
{int C[size][W];//用于存储子问题的最优解for(int i = 0; i < size; ++i)for(int j = 0; j < W; ++j)C[i][j] = 0;for(int i = 1; i < size; ++i)for(int j = 1; j < W; ++j){if(w[i-1] < j){C[i][j]=max(C[i-1][j],C[i-1][j-w[i-1]+p[i-1]);}else C[i][j] = C[i-1][j];}
}

8.最优二叉查找树

给定 $n$ 个关键字组成的有序序列 $S=\{s_1,s_2,...,s_n\}$ ，用这些关键字构造一棵二叉查找树 $T$ ，该树具有性质：存储于每个节点的元素大于左子树中任一个节点中的元素，小于其右子树中任意节点的元素。

通常用平均比较次数来作为衡量不同二叉查找树查找效率的标准。设在表示为 $S=\{s_1,s_2,...,s_n\}$ 的二叉查找树 $T$ 中，元素 $s_i$ 的结点深度为 $c_i(1\leqslant i\leqslant n)$ ，查找概率为 $p_i$ ；虚节点为 $\{e_0,e_1,...,e_n\}$ ， $e_j$ 的结点深度为 $d_j$ ，查找概率为 $q_j(0\leqslant j\leqslant n)$ 。那么平均比较次数通常被定义为：

$C=\sum_{i=1}^{n}p_i(1+c_i)+\sum_{j=0}^{n}q_jd_j$

最优二叉查找树是在所有表示有序序列的二叉查找树中，具有最小平均比较次数的二叉树。

8.1最优子结构分析

将由实结点 $\{s_1,s_2,...,s_n\}$ 和虚结点 $\{e_0,e_1,...,e_n\}$ 构成的二叉查找树记为 $T(1,n)$ 。设定元素 $s_k$ 作为该树的根结点， $1\leqslant k\leqslant n$ 。则二叉查找树 $T(1,n)$ 的左子树由实结点 $\{s_1,s_2,...,s_{k-1}\}$ 和虚结点 $\{e_0,e_1,...,e_k-1\}$ 组成，记为 $T(1,k-1)$ ，而右子树由实结点 $\{s_{k-1},...,s_{n}\}$ 和虚结点 $\{e_{k-1},...,e_{n}\}$ 组成，记为 $T(k+1,n)$ 。

如果 $T(1,n)$ 是最优二叉查找树，假设它的左子树不是一个最优二叉查找树，也就是说存在另一个二叉查找树有更小的查找次数，那么在右子树不变的情况下，拥有该左子树的二叉查找树的效率比原树更高，那么原树就不是最优二叉查找树。则左子树 $T(1,k-1)$ 和右子树 $T(k+1,n)$ 也是最优二叉查找树。

8.2递归关系建立

设 $T(1,n)$ 的一棵由实结点 $\{s_1,s_2,...,s_j\}$ 和虚节点 $\{e_0,e_1,...,e_j\}$ 构成的最优二叉查找子树为 $T(i,j)$ ，则 $C'^{}[i][j]$ 表示 $T[i][j]$ 的平均比较次数。选定结点作为 $T[i][j]$ 的根结点，则左子树为 $T(i,k-1)$ ，右子树 $T(k+1,j)$ ，相应的比较次数分别为 $C'[i][k-1]$ 和 $C'[k+1][j]$ 。用 $p[n]$ 表示查找实结点的概率，用 $q[n]$ 表示需节点的查找概率。

$w_{ij}C'[i][j]=w_{i(k-1)}C'i][k-1]+w_{(k+1)j}C'[k+1][j]+w_{ij}$

其中 $w_{ij}=\sum_{m=i}^{j}p_m+\sum_{i=i-1}^{j}q_t~~~~~1\leqslant i\leqslant j\leqslant n$

令 $C[i][j]=w_{ij}C'[i][j]$

得到： $C[i][j]=w_{ij}+min\{C[i][k-1]+C[k+1][j]\}$

其中 $w_{ij}=w_{i(j-1)}+p_j+q_j$

8.3代码分析

#include <iostream>
#include <vector>
#include <climits>using namespace std;void build_optimal_bst(vector<int> s, vector<double> p, vector<double> q) {int n = s.size();// 初始化 C 和 R 数组vector<vector<double>> C(n + 1, vector<double>(n + 1, 0));vector<vector<int>> R(n + 1, vector<int>(n + 1, 0));// 计算 W 数组vector<vector<double>> W(n + 1, vector<double>(n + 1, 0));for (int i = 1; i <= n; ++i) {W[i][i - 1] = q[i - 1];}// 动态规划填充 C 和 R 数组for (int l = 1; l <= n; ++l) {  // 子树长度从1到nfor (int i = 0; i <= n - l; ++i) {int j = i + l;C[i][j] = numeric_limits<double>::max();for (int r = i; r < j; ++r) {double t = W[i][j] + C[i][r] + C[r + 1][j];if (t < C[i][j]) {C[i][j] = t;R[i][j] = r;}}}}// 更新 W 数组for (int l = 1; l <= n; ++l) {for (int i = 0; i <= n - l; ++i) {int j = i + l;W[i][j] = W[i][j - 1] + p[j] + q[j + 1];}}cout << "Cost matrix C:" << endl;for (int i = 0; i <= n; ++i) {for (int j = 0; j <= n; ++j) {cout << C[i][j] << " ";}cout << endl;}cout << "\nRoot position matrix R:" << endl;for (int i = 0; i <= n; ++i) {for (int j = 0; j <= n; ++j) {cout << R[i][j] << " ";}cout << endl;}
}int main() {vector<int> s = {1, 3, 5, 7};  // 有序序列 Svector<double> p = {0.15, 0.1, 0.25, 0.1};  // 查找概率 pvector<double> q = {0.05, 0.15, 0.1, 0.15, 0.05};  // 边界及间隙概率 q// 构建 OBSTbuild_optimal_bst(s, p, q);return 0;
}

算法设计与分析——动态规划

1.动态规划基础 1.1动态规划的基本思想动态规划建立在最优原则的基础上，在每一步决策上列出可能的局部解，按某些条件舍弃不能得到最优解的局部解，通过逐层筛选减少计算量。每一步都经过筛选，以每一步的最优性来保证全局的最优性…...

编程日记 2024/10/26 21:02:38

【实战篇】GEO是什么？还可以定义新的数据类型吗？

背景之前，我们学习了 Redis 的 5 大基本数据类型：String、List、Hash、Set 和 Sorted Set，它们可以满足大多数的数据存储需求，但是在面对海量数据统计时，它们的内存开销很大，而且对于一些特殊的场景&…...

编程日记 2024/10/26 21:01:34

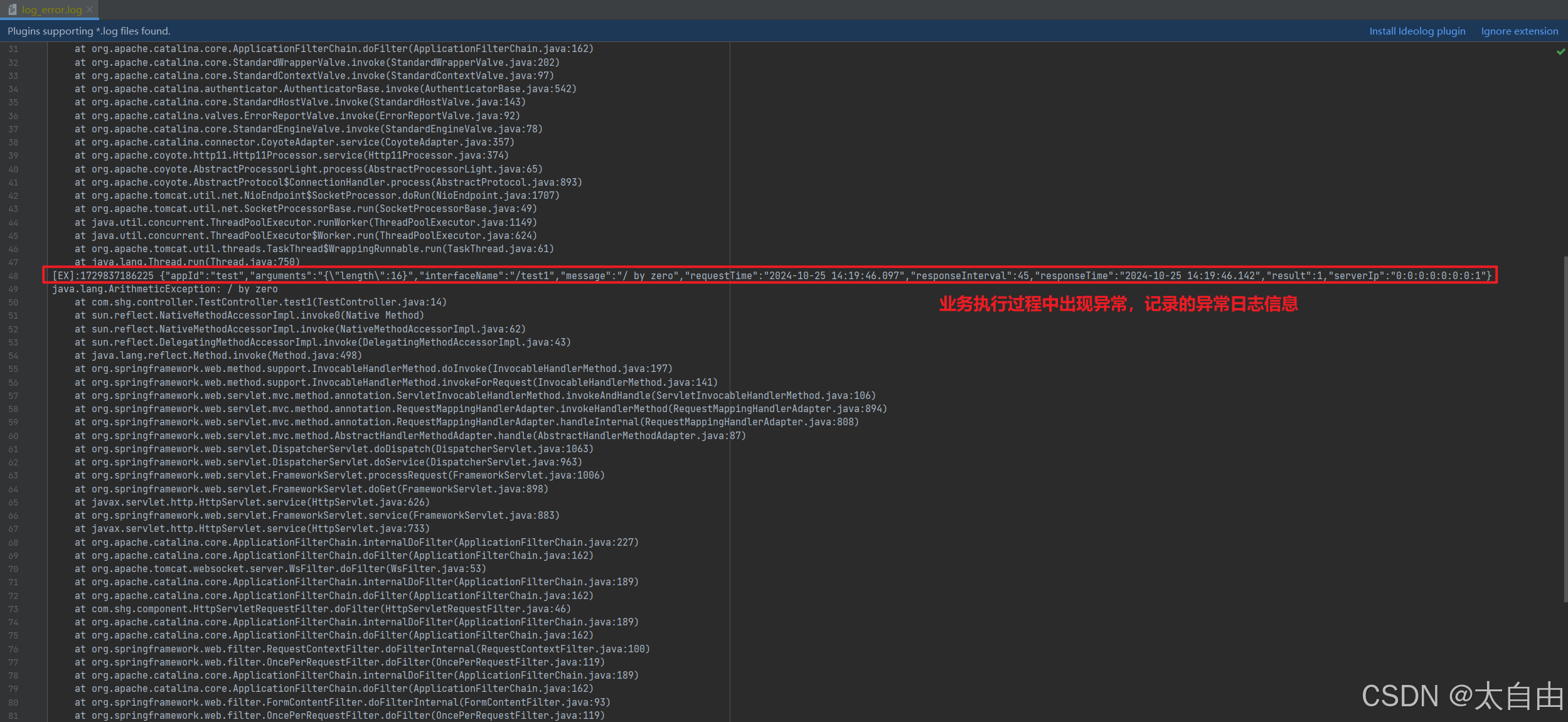
SpringBoot最佳实践之 - 项目中统一记录正常和异常日志

1. 前言此篇博客是本人在实际项目开发工作中的一些总结和感悟。是在特定需求背景下，针对项目中统一记录日志(包括正常和错误日志)需求的实现方式之一，并不是普适的记录日志的解决方案。所以阅读本篇博客的朋友，可以参考此篇博客中记录日志的…...

编程日记 2024/10/26 21:00:32

【Flutter】状态管理：高级状态管理 (Riverpod, BLoC)

当项目变得更加复杂时，简单的状态管理方式（如 setState() 或 Provider）可能不足以有效地处理应用中状态的变化和业务逻辑的管理。在这种情况下，高级状态管理框架，如 Riverpod 和 BLoC，可以提供更强大的工具…...

编程日记 2024/10/26 20:59:30

OAK相机的RGB-D彩色相机去畸变做对齐

▌低畸变标准镜头的OAK相机RGB-D对齐的方法 OAK相机内置的RGB-D管道会自动将深度图和RGB图对齐。其思想是将深度图像中的每个像素与彩色图像中对应的相应像素对齐。产生的RGB-D图像可以用于OAK内置的图像识别模型将识别到的2D物体自动映射到三维空间中去，或者产生的…...

编程日记 2024/10/26 20:57:28

smartctl硬盘检查工具

一、smartctl工具简介 Smartmontools是一种硬盘检测工具，通过控制和管理硬盘的SMART(Self Monitoring Analysis and Reporting Technology)，自动检测分析及报告技术)技术来实现的，SMART技术可以对硬盘的磁头单元、盘片电机驱动系统、硬盘…...

编程日记 2024/10/26 20:56:28

清空MySQL数据表

要清空 MySQL 数据表，您可以使用 TRUNCATE 或 DELETE 命令使用 TRUNCATE 命令 TRUNCATE 命令用于删除表中的所有数据，并重置自增 ID（如果存在）： TRUNCATE TABLE table_name;将 table_name 替换为您要清空的表的名称…...

编程日记 2024/10/26 20:55:27

2024年妈杯MathorCup大数据竞赛A题超详细解题思路

2024年妈杯大数据竞赛初赛整体难度约为0.6个国赛。A题为台风中心路径相关问题，为评价预测问题；B题为库存和销量的预测优化问题。B题难度稍大于A题，可以根据自己队伍情况进行选择。26日早六点之前发布AB两题相关解题代码论文。下面为大家带来…...

编程日记 2024/10/26 20:53:22

Kafka系列之：Kafka集群磁盘条带划分和Kafka集群磁盘扩容详细方案

Kafka系列之：Kafka集群磁盘条带划分和Kafka集群磁盘扩容详细方案一、lsblk命令二、Kafka节点磁盘条带化方案一三、Kafka节点磁盘条带化方案二四、理解逻辑区块LE五、查看kafka节点磁盘条带划分情况六、Kafka节点磁盘扩容一、lsblk命令 lsblk命令用于列出块设备的信息，包括磁…...

编程日记 2024/10/26 20:51:16

【LeetCode】修炼之路-0007- Reverse Integer （整数反转）【python】

题目 Reverse Integer Given a signed 32-bit integer x, return x with its digits reversed. If reversing x causes the value to go outside the signed 32-bit integer range [-231, 231 - 1], then return 0. Assume the environment does not allow you to store 64-b…...

编程日记 2024/10/26 20:48:14