算法刷题-小猫爬山
本题来源165. 小猫爬山 - AcWing题库
翰翰和达达饲养了 NN 只小猫,这天,小猫们要去爬山。
经历了千辛万苦,小猫们终于爬上了山顶,但是疲倦的它们再也不想徒步走下山了(呜咕>_<)。
翰翰和达达只好花钱让它们坐索道下山。
索道上的缆车最大承重量为 W,而 N 只小猫的重量分别是 C1、C2……CN。
当然,每辆缆车上的小猫的重量之和不能超过 W。
每租用一辆缆车,翰翰和达达就要付 1 美元,所以他们想知道,最少需要付多少美元才能把这 N只小猫都运送下山?
输入格式
第 1 行:包含两个用空格隔开的整数,N 和 W。
第 2..N+1行:每行一个整数,其中第 i+1行的整数表示第 i 只小猫的重量 Ci。
输出格式
输出一个整数,表示最少需要多少美元,也就是最少需要多少辆缆车。
数据范围
1≤N≤18,
1≤Ci≤W≤10^8
输入样例:
5 1996
1
2
1994
12
29
输出样例:
2我们想一下,如若使用DFS进行解答(暴力解答)。
其实许多类似的题难的地方不在于DFS本身,而在于题目的转化,即要想一种枚举的策略(或者说一种树形枚举的结构),能将所有可能性都考虑到。
首先没有任何想法的时候,不妨从问题最表面的地方出发,问题中有小猫的体重,还问我们需要的小车的数量。-->那么我们可以尝试一下从这个找到切入点,比如枚举每一个小猫,或者枚举每一个小车?
这里,我们来“试错”一下。
假如我们要枚举小猫。
我们要如何枚举呢?
那肯定是要一个一个枚举啊。
找到一个小猫后面需要干什么?(这里从开始想不好想。从结束想也不好想,那么不妨从中间开始想,但是这样的话,我们需要假设之前的已经选好了几个小车了比如{猫1,猫3}、{猫2,猫4}。现在到“猫5”了,该如何操作呢?)
假设我们已经选到“猫5”了,那么很自然,我们要从组1到组2一个一个枚举能不能装入,如果这两个组都枚举完了的话,那就要新建一个组了{猫1,猫3}、{猫2,猫4}、{猫5}。
注意,这里我们是进行了两层嵌套的枚举。
我们先不要想搜索过程中哪些可行,哪些不可行,我们先把所有的都枚举出来(搭建好这个结构再进行剪枝)
#include<iostream>
#include<algorithm>
#include<string>
using namespace std;
const int N = 19;
int car[N];//这里存放每个车,已经有多少重量了,因为题目不要求输出方案,所以不需要单独存储每个车上有哪个具体的小猫
int cat[N];//每个小猫的重量
int n,W;
int ans = N;void dfs(int num_cat,int counter_car){// num_cat:当前枚举到第几只猫,counter_car:已经使用几辆车了if(counter_car>=ans) return; //没有这个会Tif(num_cat>=n){//当枚举完小猫,这一个深度(方案)完成ans = min(ans,counter_car);//只有这个方案数小时,才更新return ;//方案完成要返回}for(int i=0;i<counter_car;i++){//这里枚举到这只小猫了,就要从之前已经装车的上面依次枚举每辆车if(car[i]+cat[num_cat]<=W){//只有小猫可以放入这辆车,才进行操作car[i]+=cat[num_cat]; //选择的车重量加dfs(num_cat+1,counter_car); //开始枚举下一只小猫,但是总车的数量不变car[i]-=cat[num_cat]; //恢复现场,看一下下一辆车}}car[counter_car] = cat[num_cat];//新开一个车dfs(num_cat+1,counter_car+1);car[counter_car]=0;//恢复现场}int main(){cin>>n>>W;for(int i=0;i<n;i++) cin>>cat[i];sort(cat,cat+n);//从小到大排序reverse(cat,cat+n);//反转顺序dfs(0,0);//当前从第0只猫开始搜,当前使用的车的数量是0cout<<ans<<endl;return 0;
}总结一下这类将n个物品放入有限制的容器中,并且求最小容器数的解法:
枚举这n个物品,枚举到第i个物品时,先给第i个物品选择要放入的地方(这个地方可以是已经有的,也可以是新建的。然后再去枚举下一个物品。)。在这其中,如何来“标记”已经选好的地方呢?可以将“已经使用的数量”作为参数,放入DFS的参数中。
相关文章:

算法刷题-小猫爬山
本题来源165. 小猫爬山 - AcWing题库 翰翰和达达饲养了 NN 只小猫,这天,小猫们要去爬山。 经历了千辛万苦,小猫们终于爬上了山顶,但是疲倦的它们再也不想徒步走下山了(呜咕>_<)。 翰翰和达达只好花…...
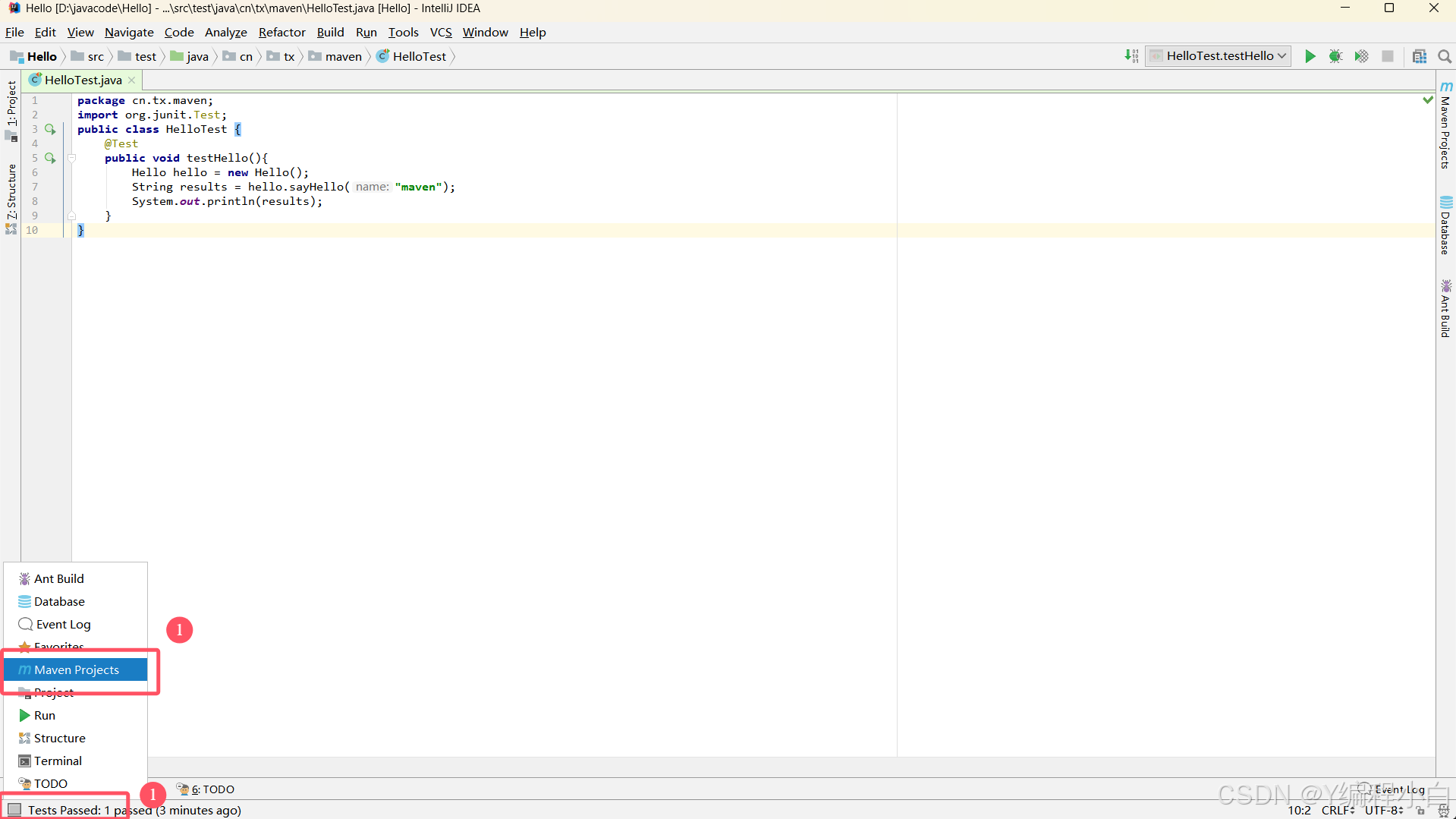
Maven项目管理工具-初始+环境配置
1. Maven的概念 1.1. 什么是Maven Maven是跨平台的项目管理工具。主要服务于基于Java平台的项目构建,依赖管理和项目信息管理。 理想的项目构建:高度自动化,跨平台,可重用的组件,标准化的流程 maven能够自动下载依…...

【JavaEE初阶】网络编程TCP协议实现回显服务器以及如何处理多个客户端的响应
前言 🌟🌟本期讲解关于TCP/UDP协议的原理理解~~~ 🌈感兴趣的小伙伴看一看小编主页:GGBondlctrl-CSDN博客 🔥 你的点赞就是小编不断更新的最大动力 🎆那么废话不多说…...

Android 中的串口开发
一:背景 本文着重讲安卓下的串口。 由于开源的Android在各种智能设备上的使用越来越多,如车载系统等。在我们的认识中,Android OS的物理接口一般只有usb host接口和耳机接口,但其实安卓支持各种各样的工业接口,如HDM…...

TensorRt OP
在TensorRT中,OP(Operations,操作)是指网络中的基本计算单元,类似于数学中的运算符。每个OP执行一个特定的计算任务,例如卷积、矩阵乘法、激活函数等。TensorRT通过识别和优化这些OP来提高深度学习模型的推…...

构建负责任的人工智能:数据伦理与隐私保护
构建负责任的人工智能:数据伦理与隐私保护 目录 🌟 数据伦理的重要性📊 公平性评估:实现无偏差的模型🔒 数据去标识化:保护用户隐私的必要手段🔍 透明性与问责:建立可信的数据处理…...

微信小程序live-pusher和video同时使用,video播放声音时时大时小
一、遇到的问题 微信小程序live-pusher和video同时使用,video播放声音时有时无时大时小 二、排查流程 业务是模拟面试,每道题一个推流live-pusher和一个面试题video,一次面试有多道面试题,页面就一个live-pusher和一个video,切换面试题时给live-pusher和video重新赋值u…...

MySQL 分库分表实战
在当今互联网时代,数据量的增长呈爆炸式趋势,传统的单库单表架构已经难以满足大规模数据存储和高并发访问的需求。MySQL 分库分表技术应运而生,它可以有效地提高数据库的性能、扩展性和可用性。本文将详细介绍 MySQL 分库分表的实战经验。 一…...

MySQL—CRUD—进阶—(二) (ಥ_ಥ)
文本目录: ❄️一、新增: ❄️二、查询: 1、聚合查询: 1)、聚合函数: 2)、GROUP BY子句: 3)、HAVING 子句: 2、联合查询: 1)、内连接…...

时序分解 | TTNRBO-VMD改进牛顿-拉夫逊算法优化变分模态分解
时序分解 | TTNRBO-VMD改进牛顿-拉夫逊算法优化变分模态分解 目录 时序分解 | TTNRBO-VMD改进牛顿-拉夫逊算法优化变分模态分解效果一览基本介绍程序设计参考资料 效果一览 基本介绍 (创新独家)TTNRBO-VMD改进牛顿-拉夫逊优化算优化变分模态分解TTNRBO–VMD 优化VMD分解层数K和…...

2024“源鲁杯“高校网络安全技能大赛-Misc-WP
Round 1 hide_png 题目给了一张图片,flag就在图片上,不过不太明显,写个python脚本处理一下 from PIL import Image # 打开图像并转换为RGB模式 img Image.open("./attachments.png").convert("RGB") # 获取图像…...

CSS行块标签的显示方式
块级元素 标签:h1-h6,p,div,ul,ol,li,dd,dt 特点: (1)如果块级元素不设置默认宽度,那么该元素的宽度等于其父元素的宽度。 (2)所有的块级元素独占一行显示. (3ÿ…...

Go 语言中的 for range 循环教程
在 Go 语言中,for range 循环是一个方便的语法结构,用于遍历数组、切片、映射和字符串。本教程将通过示例代码来帮助理解如何在 Go 中使用 for range 循环。 package mainimport "fmt"func main() {// 遍历切片并计算和nums : []int{2, 3, 4}…...

青训营 X 豆包MarsCode 技术训练营--小M的比赛胜场计算
问题描述 小M参加了一场n个人的比赛,比赛规则是所有选手两两对决。每个人有一个能力值,对应着他们的序号。参赛者同时被分为黄色或蓝色两种颜色。比赛胜负的规则如下: 当比赛双方颜色不同时,能力值大的选手获胜; 当比…...

海王3纯源码
海王3是一款热门的捕鱼类游戏,其纯源码为开发者提供了一个完整的游戏开发基础。该源码包括客户端和服务端的完整架构,支持多人在线竞技模式和丰富的游戏玩法。服务端采用C语言编写,并使用MySQL数据库来存储玩家数据,确保数据处理的…...

【ShuQiHere】Linux 系统中的硬盘管理详解:命令与技巧
【ShuQiHere】 💽 在 Linux 系统中,硬盘管理不仅仅是存储数据的操作,更涉及系统性能、数据安全和稳定性的优化。无论你是系统管理员、开发者还是 Linux 爱好者,掌握硬盘管理的基础操作都非常有用。本文将从硬盘健康检查、分区管理…...

数据结构之堆和二叉树的简介
1.树 1.1 树的概念与结构 如图所示,树是⼀种非线性的数据结构,它是由 n (n>0) 个有限结点组成⼀个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。 …...

微信小程序上传图片添加水印
微信小程序使用wx.chooseMedia拍摄或从手机相册中选择图片并添加水印, 代码如下: // WXML代码:<canvas canvas-id"watermarkCanvas" style"width: {{canvasWidth}}px; height: {{canvasHeight}}px;"></canvas&…...

xshell5找不到匹配的host key算法
xshell5找不到匹配的host key算法,是因为电脑客户端不支持服务器的算法,因此需要再服务器增加算法。 下面以Ubuntu系统为例,修改下面的文件 sudo vim /etc/ssh/sshd_config 增加下面算法 KexAlgorithms diffie-hellman-group-exchange-…...

Linux中安装Tomcat
文章目录 一、Tomcat介绍1.1、Tomcat是什么1.2、Tomcat的工作原理1.3、Tomcat适用的场景1.4、Tomcat与Nginx、Apache比较1.4.1、优势1.4.2、劣势1.4.3、定位功能 1.5、Tomcat 的主要组件1.6、Tomcat 的主要配置文件 二、Tomcat安装2.1、查看可用的JDK2.2、安装OpenJDK 112.3、配…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果