递归相关练习

21. 合并两个有序链表 - 力扣（LeetCode）

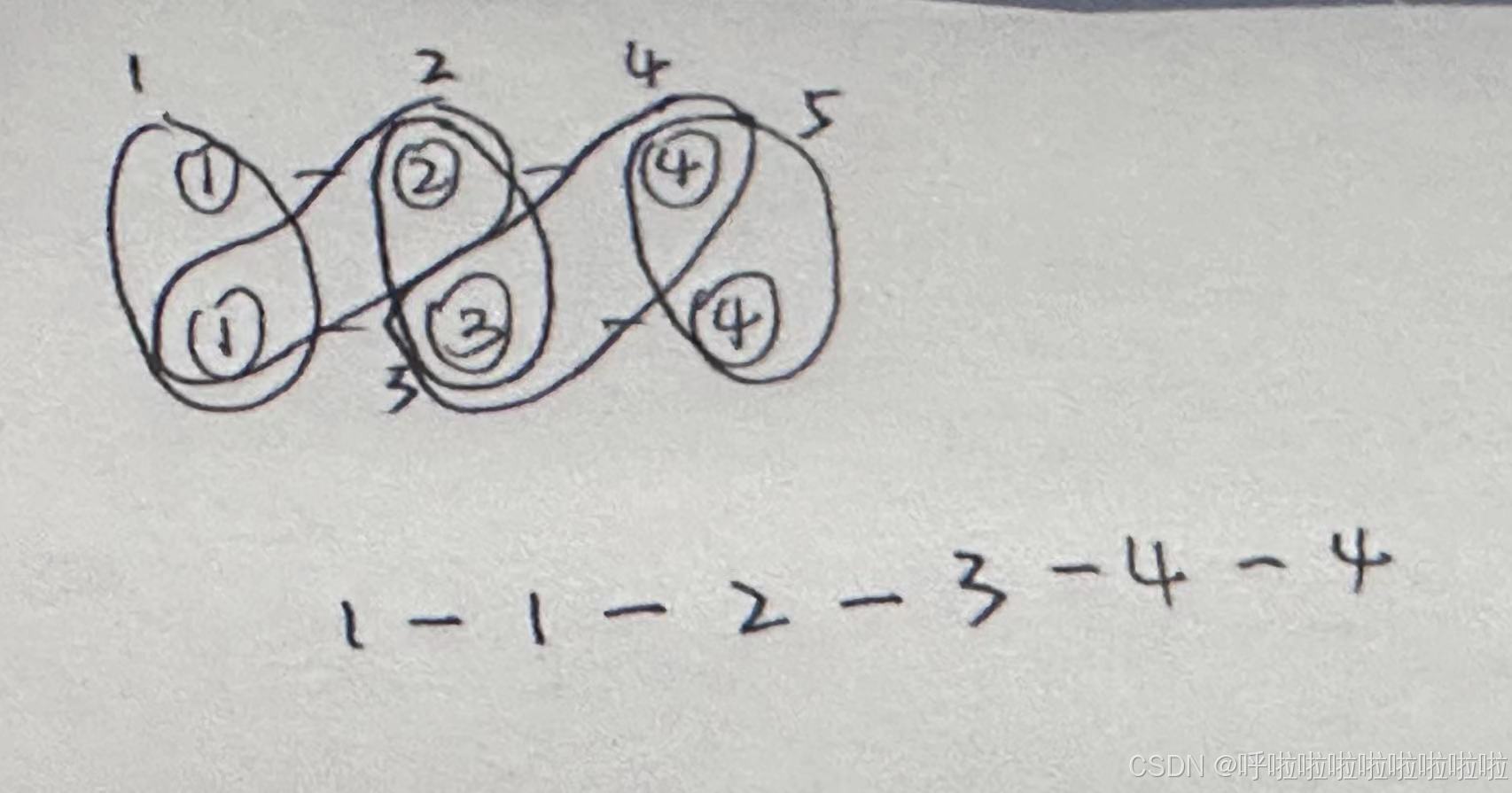
重复子问题：将l1的头节点跟l2的头结点比较 得到一个较小的头节点l1 随后继续比较 将l1后面一个节点跟l2第一个节点比较  又得到一个较小的节点 不断下去

递归出口：当l1或者l2为空时候 返回另一个即可

---

 206. 反转链表 - 力扣（LeetCode）

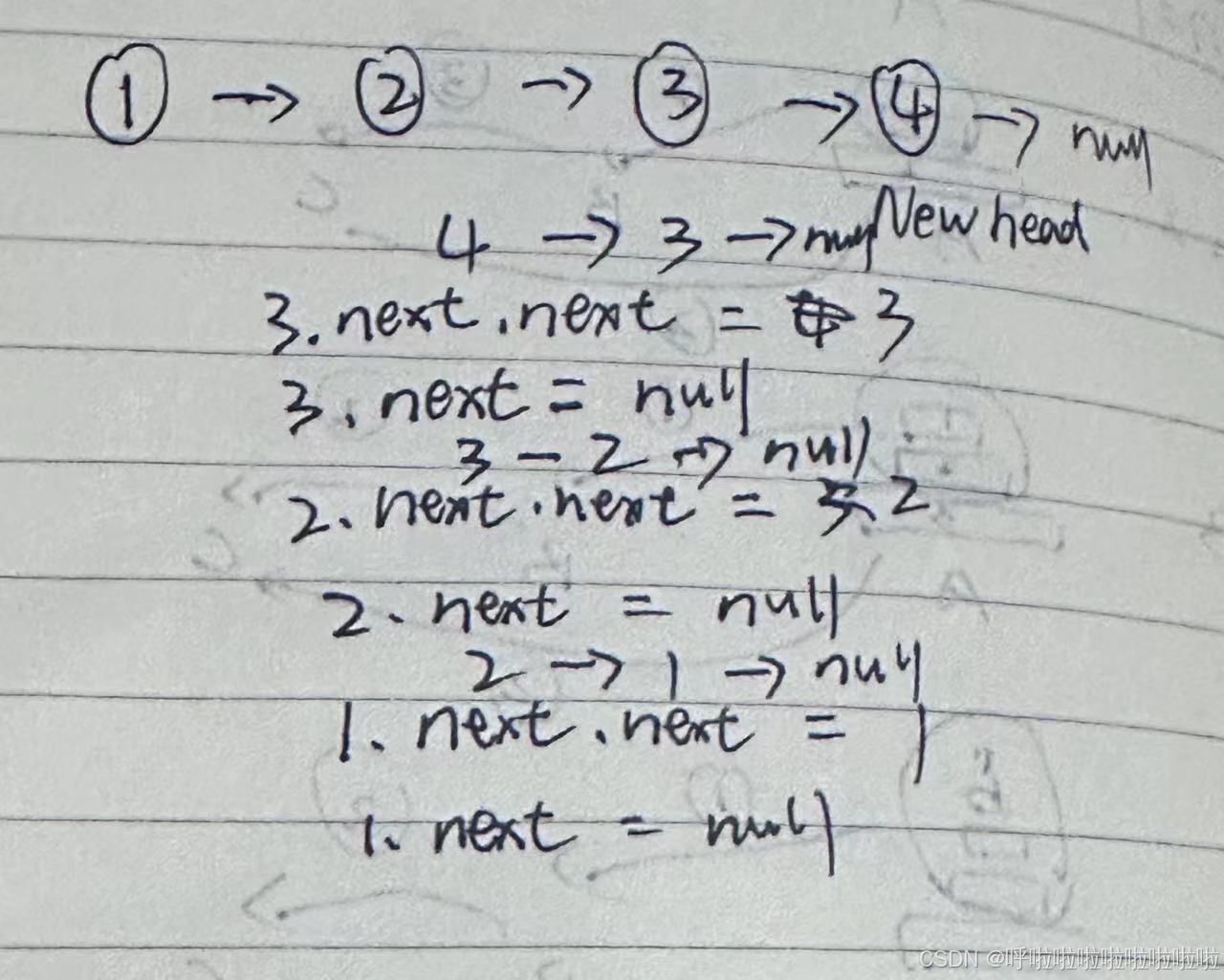
解题思路 ：不进行处理，先让head走到最后一个节点，如果有head为空或者下一个节点为空的话，直接返回最后一个节点 并做个新节点的头 紧接着回退 并且重复每个一样的子过程

让当前节点后面节点指向自己  并且自己指向空

---

 24. 两两交换链表中的节点 - 力扣（LeetCode）

 

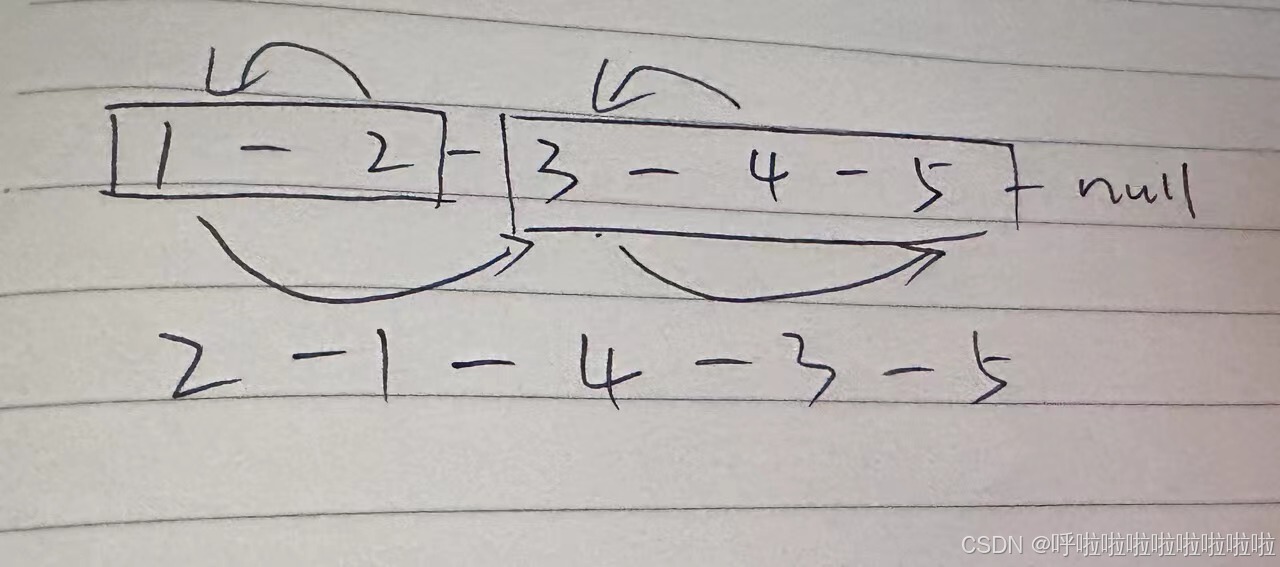
思路：两两交换 先遍历到最后一个节点
递归出口：看看最后一个节点或下一个节点是否为空 就回退

子问题: 1->2  3->4 解决思路一样

函数头设计 dfs(head.next.next)
将4->3  3->4.next        2->1 1->2.next

最后返回head.next

    public ListNode swapPairs(ListNode head) {if (head == null || head.next == null) {return head;}ListNode cur = swapPairs(head.next.next);ListNode ret = head.next;ret.next = head;head.next = cur;return ret;}

---

​​​​​​​50. Pow(x, n) - 力扣（LeetCode）

 

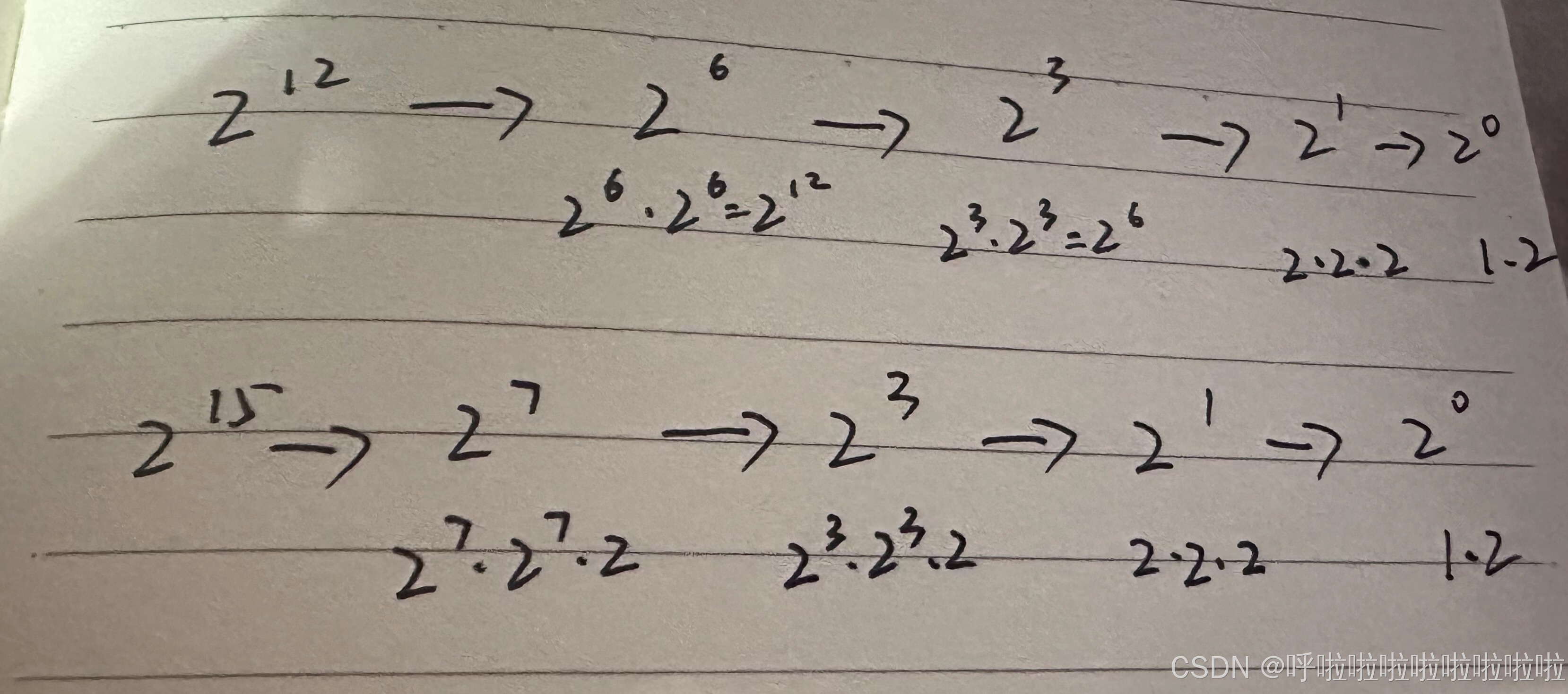
解题思路：当求一个数的次方时，用循环遍历的方式必然效率是低下的 

如图 ：当求2^12时候 我们可以先求2^6 当求2^6时候 我们可以求2^3 

当求2^3 时候 求2^1 再乘以x本身 即可求出

所以可以得出可以使用到递归求解 
递归出口：当 n=0时 返回1即可

细节：如果n为负数  只需用1.0除法运算