当前位置： 首页 > news >正文

ETF申购赎回指南：详解注意事项与低费率券商推荐！

news 文章来源：https://blog.csdn.net/weixin_eng02048/article/details/143320970 2025/1/17 22:04:43

​ETF 申购&赎回

ETF申购赎回是个啥业务？

01

ETF申购、赎回是一种交易委托方式，指投资者通过申购方式(买入方向)获得ETF份额，通过赎回的方式（卖出方向）换掉/卖出ETF份额。ETF申购，通常是通过一篮子成分股换得基金份额；ETF赎回通常是得到一篮子成分股。

ETF申赎是在什么场所进行的？咱们普通投资者做ETF申赎一般都是通过沪深交易所进行的。

ETF申赎需要用什么账户参与？ETF申赎需要投资人有开立相应的A股股东账户或封闭式基金账户，具体的账户要求咱们也可以在基金文件里面查阅的。A股股东账户的交易品种范围是大于封闭式基金账户的，所以投资者只需要开立有沪深A股股东账户就满足做申赎的条件了。

参与ETF申赎前务必要做什么？

02

那必须是投资人仔细阅读基金合同、招募说明书、产品资料概要等基金法律文件呀！了解自己投资的品种是什么，有什么投资风险，自己的风险承受能力是否适合参与等等。申赎下单时务必要了解所申赎产品的投资风险和产品特征等等等要素哦。

1、申购ETF是用可用资金还是可取资金申购？

目前参与ETF申购需要用到可取资金的ETF品种有跨境ETF、现金债ETF、黄金ETF、商品期货ETF等交易所规定的其他品种。其他如股票ETF的申赎涉及部分现金替代的则可根据申赎清单使用一部分可用资金和一篮子股票进行申购。

2、ETF申购、赎回是按净值结算吗？

不是。ETF申赎并不是像普通开放式基金那样按申赎当日日终管理人公布的净值确认份额或者确认赎回金额。而是根据ETF申赎清单中的相关篮子的实际交易价格、费用等进行结算的。ETF的净值更主要作用是为投资决策提供一个参考。

3、ETF申购、赎回有起点吗？

有的。ETF申赎、赎回一般起点在100万份左右不等。咱可根据每日公布的申赎清单内的最小申赎单位进行下单。

相关文章：

ETF申购赎回指南：详解注意事项与低费率券商推荐！

​ETF 申购&赎回 ETF申购赎回是个啥业务？ 01 ETF申购、赎回是一种交易委托方式，指投资者通过申购方式(买入方向)获得ETF份额，通过赎回的方式（卖出方向）换掉/卖出ETF份额。ETF申购，通常是通过一篮子成…...

编程日记 2024/10/29 12:12:43

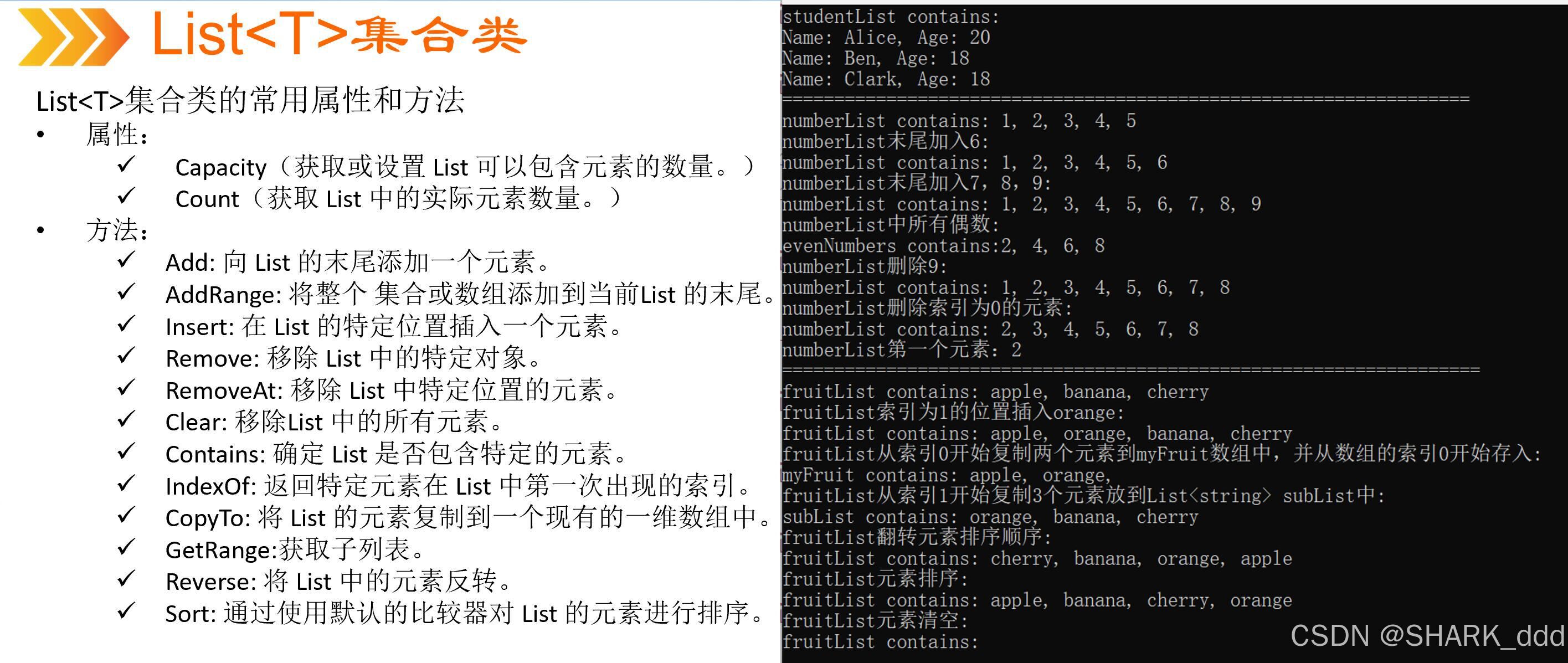
List＜T＞属性和方法使用

//author：shark_ddd using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks;//使用函数来减少长度namespace List_T {class Student{public string Name { get; set; }public int Age { get; set; …...

编程日记 2024/10/29 12:09:36

记一次：使用使用Dbeaver连接Clickhouse

前言：使用了navicat连接了clickhouse我感觉不太好用，就整理了一下dbeaver连接 0、使用Navicat连接clickhouse 测试连接 但是不能双击打开，可是使用命令页界面，右键命令页界面，然后可以用sql去测试 但是不太好用&#…...

编程日记 2024/10/29 12:06:33

Java面向对象编程进阶（四）

Java面向对象编程进阶（四） 一、equals()方法的使用二、toString()方法的使用三、复习 一、equals()方法的使用 适用性：任何引用数据都可以使用。 自定义的类在没有重写Object中equals()方法的情况下，调用的就是Object类中声明的…...

编程日记 2024/10/29 12:03:30

【51单片机】第一个小程序 —— 点亮LED灯

学习使用的开发板：STC89C52RC/LE52RC 编程软件：Keil5 烧录软件：stc-isp 开发板实图： 文章目录 单片机介绍LED灯介绍练习创建第一个项目点亮LED灯LED周期闪烁 单片机介绍 单片机，英文Micro Controller Unit&#xff0…...

编程日记 2024/10/29 12:02:29

如何通过自动化有效地简化 Active Directory 操作？

我们都知道规模稍微大一点的企业为了便于计算机的管理，基本都上了微软的AD域控制器。 那么肯定就会存在这么一个问题， 不断的会有计算机加入或者是退出域控制器，批量的创建、修改、删除AD域用户，如果企业的架构需要改变&#xff…...

编程日记 2024/10/29 12:01:28

Java-POI导出EXCEL（动态表头）

1、主要功能 导出excel&#xff0c;表头有固定的和动态的。动态表头之间不能穿插固定表头。 2、使用方法 引入下方两个工具类&#xff0c;定义excel固定表头类。调用方法即可。 调用方法&#xff1a; ExcelDynamicHeader<MajorNameChangeReport> ledgerSafetyProblemEx…...

编程日记 2024/10/29 11:59:24

利用 Direct3D 绘制几何体—9.流水线状态对象

到目前为止展示过编写输入布局描述、创建顶点着色器和像素着色器&#xff0c;以及配置光栅器状态组这 3 个步骤。接下来讲如何将这些对象绑定到图形流水线上&#xff0c;用以实际绘制图形。大多数控制图形流水线状态的对象被统称为流水线状态对象&#xff08;Pipeline State Ob…...

编程日记 2024/10/29 11:58:23

【开源项目】libfaketime安装、使用——小白教程

项目 Github&#xff1a;GitHub - wolfcw/libfaketime: libfaketime modifies the system time for a single application libfaketime安装 01.切换路径&#xff0c;目标路径&#xff1a;/usr/local &#xff08;在/usr/local路径下git clone 开源项目) 切换路径指令: cd …...

编程日记 2024/10/29 11:57:22

java.util.concurrent包

java.util.concurrent包是Java中用于并发编程的重要工具集&#xff0c;提供了丰富的并发原语和组件&#xff0c;以简化多线程编程的复杂性&#xff0c;并帮助开发者编写高效、可伸缩和线程安全的并发程序。其主要功能包括以下几个方面&#xff1a; 一、线程池和任务执行框架 …...

编程日记 2024/10/29 11:56:17

Django创建项目模块+创建映射类+视图

确保你的项目已经正确链接数据库 链接数据库的工具有很多,数据库的种类也有很多&#xff0c;我使用的数据库是mysql&#xff0c;工具是pmysql&#xff0c;使用pymysql链接数据库&#xff0c;在settings文件中这么设置&#xff1a; DATABASES {# default: {# ENGINE: dja…...

编程日记 2024/10/29 11:55:15

使用AMD GPU和LangChain构建问答聊天机器人

Question-answering Chatbot with LangChain on an AMD GPU — ROCm Blogs 作者&#xff1a;Phillip Dang 2024年3月11日 LangChain是一个旨在利用语言模型强大功能来构建前沿应用程序的框架。通过将语言模型连接到各种上下文资源并基于给定的上下文提供推理能力&#xff0c;L…...

编程日记 2024/10/29 11:52:12

2024年808数据结构答案

1.已知带头结点单链表&#xff0c;H为头指针。设计一个算法&#xff0c;查找到链表的第m个结点(不包含头结点)&#xff0c;并将元 素值为X的结点插入到该结点后&#xff0c;形成一个新的链表。 // 定义单链表节点结构 typedef struct Node {int data;struct Node* next; } Nod…...

编程日记 2024/10/29 11:50:09

Amazon Linux 2023 安装 Docker

Amazon Linux 2023 安装 Docker 1. 简介 在公司需要将代码部属到 Amazon Linux 2023 系统上时&#xff0c;去 Docker 官方文档里面看也没有针对该系统的部属文档。虽然有通用的 Linux 部属方案但不能应用包管理工具。 首先执行yum、dnf、apt&#xff0c;执行yum和dnf都有正确…...

编程日记 2024/10/29 11:49:06

接口测试（八）jmeter——参数化（CSV Data Set Config）

一、CSV Data Set Config 需求&#xff1a;批量注册5个用户&#xff0c;从CSV文件导入用户数据 1. 【线程组】–>【添加】–>【配置元件】–>【CSV Data Set Config】 2. 【CSV数据文件设置】设置如下 3. 设置线程数为5 4. 运行后查看响应结果...

编程日记 2024/10/29 11:48:04

GGD证明推导学习

GGD证明推导学习 这篇文章&#xff0c;建议先看相关的论文。这篇是我读证明的感悟&#xff0c;因此&#xff0c;不会论文的主体内容 首先&#xff0c;给出命题&#xff1a; DGI的sumary向量是一个常数 给定一个图&#xff1a; G { X ∈ R N D , A ∈ R N N } \mathcal{G…...

编程日记 2024/10/29 11:47:03

Flink难点和高频考点：Flink的反压产生原因、排查思路、优化措施和监控方法

目录 反压定义 反压影响 WebUI监控 Metrics指标 backPressureTimeMsPerSecond idleTimeMsPerSecond busyTimeMsPerSecond 反压可视化 资源优化 算子优化 数据倾斜优化 复杂算子优化 背压机制 反压预防 性能调优 内置工具 第三方工具 反压定义 在探讨Flink的性…...

编程日记 2024/10/29 11:45:01

Swarm - Agent 编排工具

文章目录 一、关于 Swarm&#xff08;实验性、教育性&#xff09;为什么选择蜂群文档 二、安装使用安装基本用法其它示例 三、Running Swarmclient.run()ArgumentsResponse字段 四、AgentFields Agent指令函数切换和更新上下文变量函数模式 流媒体评估工具 一、关于 Swarm&…...

编程日记 2024/10/29 11:43:59

使用Python中的jieba库进行简单情感分析

在自然语言处理&#xff08;NLP&#xff09;领域&#xff0c;情感分析是一项重要的任务&#xff0c;它可以帮助我们理解文本背后的情感倾向。本文将通过一个简单的例子来介绍如何使用Python的jieba库对中文文本进行基本的情感分析。 1. 环境准备 首先&#xff0c;确保已经安装…...

编程日记 2024/10/29 11:42:59

`pip` 下载速度慢

pip 下载速度慢&#xff08;例如只有 50KB/s&#xff09;可能由多个因素导致&#xff0c;以下是一些常见原因和解决方法&#xff1a; 1. 使用国内镜像源 国内访问 PyPI 服务器可能会较慢&#xff0c;您可以通过配置国内镜像源来提升下载速度。以下是一些常用的国内镜像源&…...

编程日记 2024/10/29 11:40:55

【WRF数据准备】基于GEE下载静态地理数据-叶面积指数LAI及绿色植被率Fpar

【WRF数据准备】基于GEE下载静态地理数据 准备：WRF所需静态地理数据（Static geographical data）数据范围说明基于GEE下载叶面积指数及绿色植被率GEE数据集介绍数据下载：LAI（叶面积指数）和Fpar（绿色植被率）数据处理：基于Python处理为单波段LAI数据参考GEE的介绍可参见另…...

编程日记 2024/10/29 11:39:51

网管平台（进阶篇）：网管软件的配置方式

正确选择网管软件配置方式对于确保网络运行的高效性、稳定性和安全性至关重要&#xff0c;因为它直接影响到网络管理的灵活性、监控的深度以及故障响应的速度&#xff0c;从而保障整体网络环境的顺畅运行和业务连续性。下面我们就分别介绍一下。 一、集中式网络管理配置 在集…...

编程日记 2024/10/29 11:38:47

推荐系统中的AB测试

在现代互联网平台中&#xff0c;推荐系统起着至关重要的作用&#xff0c;无论是视频平台、社交网络还是电商网站&#xff0c;推荐系统都能够帮助用户找到最感兴趣的内容。为了不断优化推荐效果&#xff0c;AB测试&#xff08;A/B Testing&#xff09;作为评估新算法或功能改进的…...

编程日记 2024/10/29 11:36:46

.NET 8 Web API 中的身份验证和授权

本次介绍分为3篇文章&#xff1a; 1&#xff1a;.Net 8 Web API CRUD 操作.Net 8 Web API CRUD 操作-CSDN博客 2&#xff1a;在 .Net 8 API 中实现 Entity Framework 的 Code First 方法https://blog.csdn.net/hefeng_aspnet/article/details/143229912 3&#xff1a;.NET …...

编程日记 2024/10/29 11:35:45

Vue弹窗用也可以直接调用Js方法了

问题描述 在前端开发中&#xff0c;弹窗开发是一个不可避免的场景。然而&#xff0c;按照正常的逻辑&#xff0c;通过在template模板中先引用组件&#xff0c;然后通过v-if指令控制显隐&#xff0c;进而达到弹窗的效果。然而&#xff0c;这种方法却有一个严重的缺陷&#xff0…...

编程日记 2024/10/29 11:34:32

【c语言测试】

1. C语言中&#xff0c;逻辑“真”等价于&#xff08; &#xff09; 题目分析&#xff1a; “逻辑真”在C语言中通常指的是非零数。 A. 大于零的数B. 大于零的整数C. 非零的数 (正确答案)D. 非零的整数 正确答案&#xff1a;C 2. 若定义了数组 int a[3][4];&#xff0c;则对…...

编程日记 2024/10/29 11:32:27

一种将树莓派打造为游戏机的方法——Lakka

什么是Lakka&#xff1f; Lakka是一款Linux发行版&#xff0c;轻量级的&#xff0c;可将小型计算机转变为一台复古游戏机。 图1-Lakka官网&#xff0c;见参考链接[1] Lakka是RetroArch和libretro生态系统下的官方操作系统&#xff0c;前者RetroArch是模拟器、游戏引擎和媒体播…...

编程日记 2024/10/29 11:30:24

如何在 MySQL 中创建一个完整的数据库备份？

在MySQL数据库中创建一个完整的数据库备份通常不是通过编程语言直接实现的&#xff0c;而是借助MySQL提供的命令行工具mysqldump来完成。 作为Java开发者&#xff0c;我们可以编写脚本来调用这些工具&#xff0c;从而实现自动化备份。 下面我们将详细介绍如何使用Java来调度m…...

编程日记 2024/10/29 11:29:23

京准电钟HR-901GB双GPS北斗卫星时钟服务器

京准电钟HR-901GB双GPS北斗卫星时钟服务器 京准电钟HR-901GB双GPS北斗卫星时钟服务器 作为国家电力系统最重要的设备之一,卫星时间同步装置随着电力行业的发展不断有了新的要求,从单纯的具备时间数据输出能力,发展到装置状态信息上送、对用时设备的对时质量进行监测,确保站点内…...

编程日记 2024/10/29 11:28:19

uniapp使用websocket

后端java websoket中的 onOpen 中。依赖注入为null 引用&#xff1a;https://blog.csdn.net/qq_63431773/article/details/132389555 https://blog.csdn.net/weixin_43961117/article/details/123989515 https://cloud.tencent.com/developer/article/2107954 https://blog.c…...

编程日记 2024/10/29 11:24:14

做政府网站个人能做吗/关键词查询工具

OpenCV中有实现遍历文件夹下所有文件的类Directory&#xff0c;它里面包括3个成员函数&#xff1a;(1)、GetListFiles&#xff1a;遍历指定文件夹下的所有文件&#xff0c;不包括指定文件夹内的文件夹&#xff1b;(2)、GetListFolders&#xff1a;遍历指定文件夹下的所有文件夹…...

编程日记 2025/1/17 20:39:49

电商平台要投资多少钱/sem优化技巧

最近爱上了霉霉的歌曲《love story》&#xff0c;想要到网上下载钢琴谱&#xff0c;但完整的大多都是需要付费的&#xff0c;为了贯彻个人理念&#xff0c;那当然是能白嫖就不放过啦&#xff0c;在此我也顺带教一教大家不使用编程语言&#xff0c;如何爬取网页上不能下载的图片…...

编程日记 2025/1/17 19:04:40

做网站优化两年遇到的SEO常态/武汉百度搜索优化

一个人如果在乎太多也许什么都得不到&#xff0c;人生总是存在意外&#xff0c;不如意是正常&#xff0c;良好的心态能帮你度过灰色的时间&#xff0c;空间&#xff0c;帮你看到明日的太阳。 有时候想人生在世到底是为什么&#xff0c;有人也许为了理想&#xff0c;为了金钱&am…...

编程日记 2025/1/17 14:27:10

网站的服务器/合肥网站建设程序

堆排序&#xff08;Heapsort&#xff09;是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构&#xff0c;并同时满足堆积的性质&#xff1a;即子结点的键值或索引总是小于&#xff08;或者大于&#xff09;它的父节点。 堆排序的平均时间复杂度为Ο…...

编程日记 2025/1/17 13:51:28

深圳网站建设服务商万创网/免费外贸接单平台

五、接下来的目录迁移设置&#xff0c;这个没什么用&#xff0c;不用管。六、再之后是密码设置&#xff0c;这项建议正常模式下设置一下密码&#xff0c;防止别人使用你的电脑&#xff0c;不小心进入正常模式&#xff0c;结果他的操作就会全部保存下来&#xff0c;设置个密码安…...

编程日记 2025/1/17 12:05:35

重庆网站设计平台/痘痘怎么去除有效果

知识点: Canvas():创建一个空的画布&#xff0c;可以使用setBitmap()方法来设置具体的画布 Canvas(Bitmap bitmap):以bitmap对象创建一个画布&#xff0c;则将内容都绘制在Bitmap上&#xff0c;因此bitmap不能为Null Canvas(GL gl):在绘制3D效果时使用&#xff0c;与OpenGL相关…...

编程日记 2025/1/17 10:01:28