LeetCode 每日一题 2024/10/21-2024/10/27
记录了初步解题思路 以及本地实现代码;并不一定为最优 也希望大家能一起探讨 一起进步
目录
- 10/21 910. 最小差值 II
- 10/22 3184. 构成整天的下标对数目 I
- 10/23 3185. 构成整天的下标对数目 II
- 10/24 3175. 找到连续赢 K 场比赛的第一位玩家
- 10/25 3180. 执行操作可获得的最大总奖励 I
- 10/26 3181. 执行操作可获得的最大总奖励 II
- 10/27 684. 冗余连接
10/21 910. 最小差值 II
从小到大排列 小的尽量+k 大的-k
最小值mi 最大值ma
从头遍历位置i 假设nums[i]是最大一个+k的值
那么当前情况最大值为 max(nums[i]+k,ma-k)
最小值为min(nums[i+1]-k,mi+k)
更新当前情况的差值
def smallestRangeII(nums, k):""":type nums: List[int]:type k: int:rtype: int"""nums.sort()mi,ma=nums[0],nums[-1]ans = ma-min=len(nums)for i in range(n-1):cur,nxt = nums[i],nums[i+1]ans = min(ans,max(cur+k,ma-k)-min(nxt-k,mi+k))return ans10/22 3184. 构成整天的下标对数目 I
计算每个小时除以24的余数
余数相加为24的可以匹配
余数为0和12 在自己组内匹配
def countCompleteDayPairs(hours):""":type hours: List[int]:rtype: int"""l=[0]*24for h in hours:l[h%24]+=1ans = 0for i in range(1,12):ans += l[i]*l[24-i]ans+=l[0]*(l[0]-1)//2+l[12]*(l[12]-1)//2return ans10/23 3185. 构成整天的下标对数目 II
计算每个小时除以24的余数
余数相加为24的可以匹配
余数为0和12 在自己组内匹配
def countCompleteDayPairs(hours):""":type hours: List[int]:rtype: int"""l=[0]*24for h in hours:l[h%24]+=1ans = 0for i in range(1,12):ans += l[i]*l[24-i]ans+=l[0]*(l[0]-1)//2+l[12]*(l[12]-1)//2return ans10/24 3175. 找到连续赢 K 场比赛的第一位玩家
从头遍历 i 直至遇到大于他的j
如果此时已经赢了k场那么返回i
否则从j开始继续往后赢
如果到最后还没有达到k 此时的i必定是最大值 返回
def findWinningPlayer(skills, k):""":type skills: List[int]:type k: int:rtype: int"""n=len(skills)i = 0lasti = 0cnt = 0while i<n:j = i+1while j<n and skills[i]>skills[j] and cnt<k:cnt+=1j+=1if cnt==k:return icnt=1lasti = ii=jreturn lasti10/25 3180. 执行操作可获得的最大总奖励 I
从小到大排序
dp[k]表示奖励k是否可以获得
最大值为mx 能够得到的奖励不超过2*m-1
对于当前值x 最多可以到达k=x~2x-1 如果k-x存在 那么说明k可以得到
def maxTotalReward(rewardValues):""":type rewardValues: List[int]:rtype: int"""rewardValues.sort()mx = rewardValues[-1]dp=[0]*(2*mx)dp[0]=1for x in rewardValues:for k in range(2*x-1,x-1,-1):if dp[k-x]==1:dp[k]=1for i in range(len(dp)-1,-1,-1):if dp[i]==1:return i10/26 3181. 执行操作可获得的最大总奖励 II
从小到大排序 dp[k]判断奖励k是否可以获得
遍历value x 对k=x,2x-1一次查看
def maxTotalReward(rewardValues):""":type rewardValues: List[int]:rtype: int"""rewardValues.sort()if len(rewardValues)>=2 and rewardValues[-2]==rewardValues[-1]-1:return 2*rewardValues[-1]-1dp = 1for x in rewardValues:dp |= (dp & ((1<<x)-1))<<xreturn dp.bit_length()-110/27 684. 冗余连接
并查集
遍历每一条边 比树多一条边
如果两个点已经连通说明这条边是多余的
def findRedundantConnection(edges):""":type edges: List[List[int]]:rtype: List[int]"""n=len(edges)p = list(range(n+1))def find(i):if p[i]!=i:p[i]=find(p[i])return p[i]def union(i,j):p[find(i)]=find(j)for i,j in edges:if find(i)!=find(j):union(i,j)else:return [i,j]return []相关文章:

LeetCode 每日一题 2024/10/21-2024/10/27
记录了初步解题思路 以及本地实现代码;并不一定为最优 也希望大家能一起探讨 一起进步 目录 10/21 910. 最小差值 II10/22 3184. 构成整天的下标对数目 I10/23 3185. 构成整天的下标对数目 II10/24 3175. 找到连续赢 K 场比赛的第一位玩家10/25 3180. 执行操作可获得…...

不到1500元的I卡可以玩转3A大作吗?撼与科技Intel Arc A750显卡游戏性能实
一、前言 还记得2022年10月的时候,英特尔发布了Arc A750和A770显卡,和此前所发布的DG1、A380不同,这两张显卡可以说是真正意义上的游戏显卡。不知不觉间,两年已经过去了,在这两年期间,英特尔不仅在积极地打…...

STK与MATLAB互联——仿真导航卫星与地面用户间距离和仰角参数
文章目录 构建GPS星座创建单个PRN的GPS卫星创建GPS星座,并为其添加发射机 北斗星座构建搭建低轨铱星星座构建一颗轨道高度为800km/1000km/1200km的低轨卫星构建一颗轨道高度为800km/1000km/1200km的低轨卫星建立地面站,可见性分析确定地面站坐标分析单颗…...

js面试问题笔记(一)
一.热门js面试 1.简述同步和异步的区别? 同步: 浏览器访问服务器请求,用户看到页面刷新 ,重新发请求,等请求完,页面刷新,新内容出现,用户看到新内容,进行下一步操作 异步: 浏览器访问服务器请求,用户正常操作,浏览器后端进行请求,等请求完,页面不刷新,新内容也会出现,用户看到…...

pip 和 pipx 的主要区别?
特性pippipx用途用于安装Python库或命令行应用程序,可以安装带entry points的库专门用于安装和管理Python命令行工具,每个工具都在隔离的虚拟环境中运行虚拟环境不自动创建虚拟环境,需要手动使用 venv 或 virtualenv 创建自动为每个安装的工具…...

4457M数字示波器
_XLT新利通_ 4457M数字示波器 带宽500MHz到3GHz 4457M系列数字示波器产品,包含4457DM/EM/FM/GM四个产品型号,模拟通道数4、8个,带宽500MHz到3GHz,最高采样率10GSa/s,垂直分辨率8bit,最大存储深度2Gpts。…...

【永中软件-注册/登录安全分析报告】
前言 由于网站注册入口容易被黑客攻击,存在如下安全问题: 暴力破解密码,造成用户信息泄露短信盗刷的安全问题,影响业务及导致用户投诉带来经济损失,尤其是后付费客户,风险巨大,造成亏损无底洞…...

Tomcat作为web的优缺点
文章目录 优点缺点 优点 开源:Tomcat是Apache软件基金会的一个项目,这意味着它是免费且开放源代码的。这为开发者提供了高度的自由度来修改和扩展其功能。 轻量级:与一些全功能的Java EE应用服务器(如IBM WebSphere, Oracle WebL…...

conda虚拟环境中安装cuda方法、遇到的问题
conda虚拟环境中安装cuda方法、遇到的问题 文章目录 conda虚拟环境中安装cuda方法、遇到的问题conda虚拟环境中安装cudacuda.h和cuda_runtime.hpytorch运行时的CUDA版本其他问题检查包冲突nvcc -V和nvidia-smi显示的版本不一致cuda路径 conda虚拟环境中安装cuda 参考文章&…...

【CPN TOOLS建模学习】设置变迁的属性
使用Tab键在属性之间进行切换 与一个变迁相关联的四个铭文,均为可选项: 变迁名称守卫(Guard)时间代码段 变迁延迟必须是一个正整数表达式。该表达式前面加上,这意味着时间铭文的形式为 delayexpr。在添加时间铭文之前,铭文的默…...

一个简单的例子,说明Matrix类的妙用
在Android、前端或者别的平台的软件开发中,有时会遇到类似如下需求: 将某个图片显示到指定的区域;要求不改变图片本身的宽高比,进行缩放;要求最大限度的居中填充到显示区域。 以下示意图可以简单描绘该需求 以Androi…...

【C++】类和对象(四):析构函数
大家好,我是苏貝,本篇博客带大家了解C的析构函数,如果你觉得我写的还不错的话,可以给我一个赞👍吗,感谢❤️ 目录 1. 概念2. 特性 1. 概念 通过前面构造函数的学习,我们知道一个对象是怎么来的…...

linux中各目录作用及介绍
目录 1 /usr 1 /usr /usr 是 Unix-like 操作系统中的一个重要目录之一,代表可共享的用户资源(User System Resources)或 Unix Software Resource(UNIX 软件资源)。 /usr 目录通常包含了系统的许多可共享资源…...
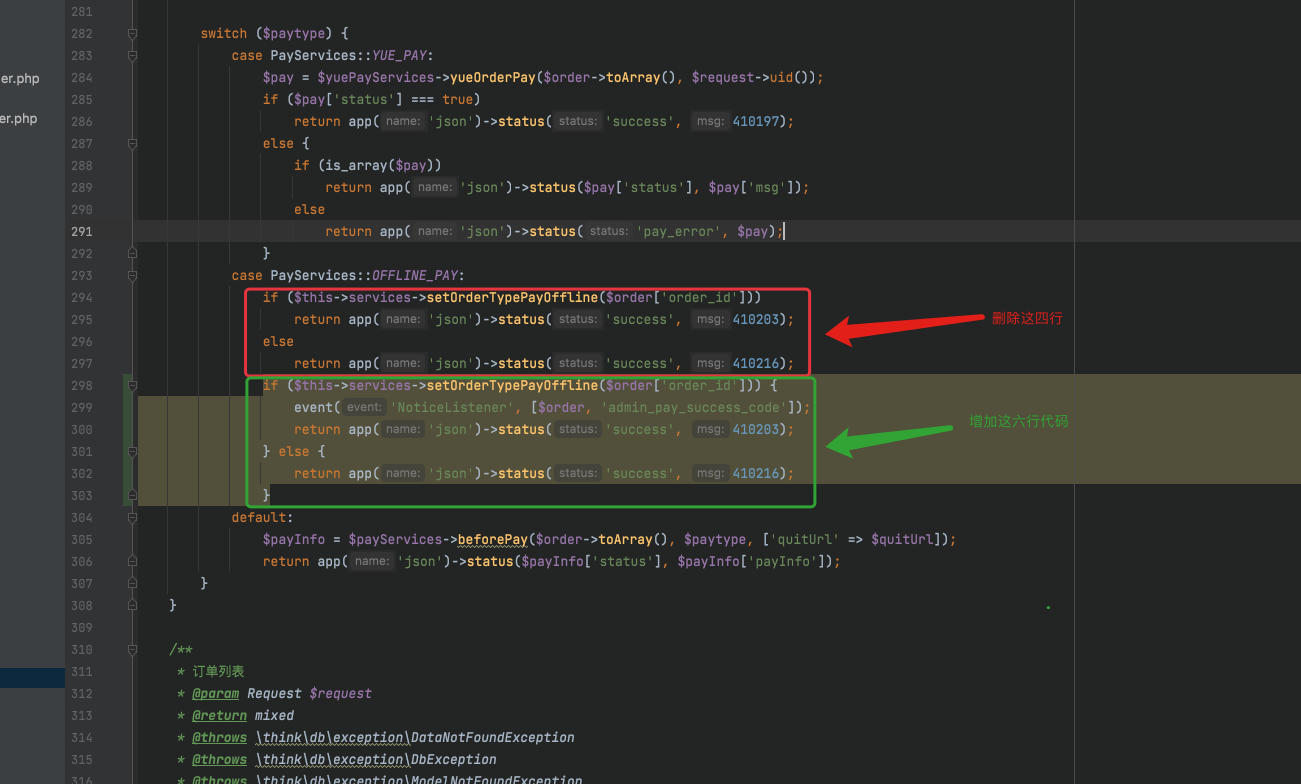
v4.7版本使用线下付款方式不给管理员发送新订单通知问题修复
在app/api/controller/v1/order/StoreOrderController.php文件中,将红框内的代码注释,加上绿框的代码即可修复 if ($this->services->setOrderTypePayOffline($order[order_id])) {event(NoticeListener, [$order, admin_pay_success_code]);retur…...

vue3中mitt和pinia的区别和主要用途,是否有可重合的部分?
在 Vue 中,Mitt 和 Pinia 是两个不同的工具,它们的主要用途和功能有所不同,但在某些方面也存在重合的部分。 区别 Mitt: Mitt 是一个简单而强大的事件总线库,用于在组件之间进行事件的发布和订阅。 它提供了一种简洁…...

飞书文档解除复制限制
解除飞书文档没有编辑器权限限制复制功能方法 方法一:使用插件 方法二: 通过调试工具删除所有的copy事件 使用插件 缺点: 只有markdown格式,如果需要其他格式需要再通过Typora等markdown编辑器转pdf,word等格式 安装插件 Cloud Do…...

vue3中ref和reactive的用法,区别和优缺点,以及使用场景
写在前头: reactive定义的数据只能修改里面的属性,不能将整个数据替换,实在要替换请使用 Object.assign(obj1, obj2);举个例子 这种写法无法直接改变obj1 let obj1 reactive({name: 猫,age: 2, });obj1 {name: 猪,age: 2, } 正确的写法…...
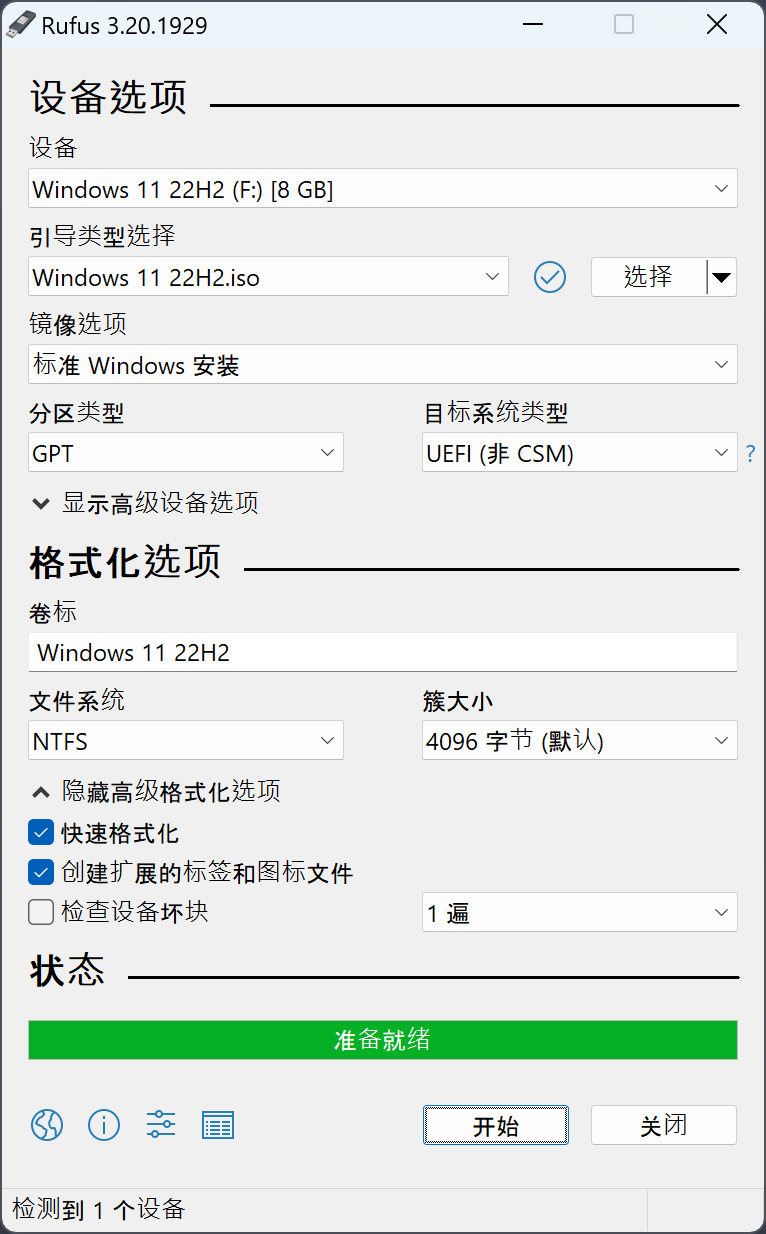
电脑技巧:Rufus——最佳USB启动盘制作工具指南
目录 一、功能强大,兼容性广泛 二、界面友好,操作简便 三、快速高效,高度可定制 四、安全可靠,社区活跃 在日常的电脑使用中,无论是为了安装操作系统、修复系统故障还是进行其他需要可引导媒体的任务,拥…...

vue的基本使用
简介 vue组件 三个部分组成:结构、样式、逻辑文本插值 类似于java的spel表达式属性绑定 綁定是单向绑定的,修改输入框无法改变原本的,只能读,不能写 <input :value="name" placeholder="Type your name"><script> export default {name: H…...

C#高级:利用 CancellationToken 实现方法超时控制,提升应用响应性
完整版: using System; using System.Threading; using System.Threading.Tasks;public class Program {public static async Task Main(){var cts new CancellationTokenSource();// 设置超时时间为10秒cts.CancelAfter(TimeSpan.FromSeconds(3));try{var resul…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...
 ----- Python的类与对象)
Python学习(8) ----- Python的类与对象
Python 中的类(Class)与对象(Object)是面向对象编程(OOP)的核心。我们可以通过“类是模板,对象是实例”来理解它们的关系。 🧱 一句话理解: 类就像“图纸”,对…...

[拓扑优化] 1.概述
常见的拓扑优化方法有:均匀化法、变密度法、渐进结构优化法、水平集法、移动可变形组件法等。 常见的数值计算方法有:有限元法、有限差分法、边界元法、离散元法、无网格法、扩展有限元法、等几何分析等。 将上述数值计算方法与拓扑优化方法结合&#…...

Java并发编程实战 Day 11:并发设计模式
【Java并发编程实战 Day 11】并发设计模式 开篇 这是"Java并发编程实战"系列的第11天,今天我们聚焦于并发设计模式。并发设计模式是解决多线程环境下常见问题的经典解决方案,它们不仅提供了优雅的设计思路,还能显著提升系统的性能…...
