文心一言 VS 讯飞星火 VS chatgpt (380)-- 算法导论24.4 12题
十二、给出一个有效算法来解决 A x ⩽ b Ax⩽b Ax⩽b 的差分约束系统,这里 b b b 的所有元素为实数,而变量 x i x_i xi 中某个给定的子集是整数。如果要写代码,请用go语言。
文心一言:
差分约束系统问题通常用于解决带有约束条件的系统,如 A x ⩽ b Ax \leqslant b Ax⩽b,其中 A A A 是一个系数矩阵, b b b 是一个约束向量,而 x x x 是我们要求解的变量向量。这些约束可以转换为图中的最短路径问题,利用 Bellman-Ford 算法来求解。
以下是解决该问题的有效算法,并使用 Go 语言实现:
算法步骤
-
转换约束为边:将每个不等式 a i j x j ⩽ b i a_{ij}x_j \leqslant b_i aijxj⩽bi 转换为图中的边 ( i , j ) (i, j) (i,j),其权重为 w i j = b i / a i j w_{ij} = b_i / a_{ij} wij=bi/aij(如果 a i j > 0 a_{ij} > 0 aij>0)。如果 a i j ⩽ 0 a_{ij} \leqslant 0 aij⩽0,则需要根据具体情况调整,例如,将不等式转化为 x i ⩾ a i j x j − b i x_i \geqslant a_{ij}x_j - b_i xi⩾aijxj−bi,从而边 ( j , i ) (j, i) (j,i) 的权重为 w j i = − b i / a i j w_{ji} = -b_i / a_{ij} wji=−bi/aij。
-
添加超级源点:引入一个超级源点 s s s,从 s s s 到每个节点 i i i 添加一条权重为 0 的边,以便可以处理所有节点的最短路径。
-
使用 Bellman-Ford 算法:应用 Bellman-Ford 算法求解从超级源点 s s s 到所有其他节点的最短路径。如果存在负权环,则问题无解(即系统不存在满足所有约束的整数解)。
-
判断整数解:检查计算出的最短路径值是否均为整数。如果不是,则问题在整数约束下无解。
Go 语言实现
package mainimport ("fmt""math"
)const (INF = math.MaxInt32
)// BellmanFord 解决差分约束系统问题
func BellmanFord(n int, edges [][]int, weights [][]float64) ([]int, bool) {// 初始化距离数组,dist[i] 表示从源点到 i 的最短距离dist := make([]int, n+1)for i := range dist {dist[i] = INF}dist[0] = 0 // 源点到自身的距离为 0// Bellman-Ford 算法for i := 0; i < n; i++ {for _, edge := range edges {u, v := edge[0], edge[1]w := float64(weights[u-1][v-1])if dist[u] != INF && dist[u]+int(math.Round(w)) < dist[v] {dist[v] = dist[u] + int(math.Round(w))}}}// 检查负权环for _, edge := range edges {u, v := edge[0], edge[1]w := float64(weights[u-1][v-1])if dist[u] != INF && dist[u]+int(math.Round(w)) < dist[v] {return nil, false // 存在负权环,无解}}// 检查是否为整数解for _, d := range dist[1:] {if float64(d) != math.Round(float64(d)) {return nil, false // 不是整数解}}return dist[1:], true // 返回从源点到各个节点的最短路径(去掉源点自身)
}func main() {// 示例:假设 A 是一个 3x3 矩阵,b 是一个长度为 3 的向量A := [][]float64{{1, -1, 0},{0, 1, 2},{-1, 0, 1},}b := []float64{4, 3, 2}n := len(b)edges := make([][]int, 0)weights := make([][]float64, n)for i := range weights {weights[i] = make([]float64, n)}// 构建图和权重for i := 0; i < n; i++ {for j := 0; j < n; j++ {if A[i][j] > 0 {edges = append(edges, []int{i + 1, j + 1})weights[i][j] = b[i] / A[i][j]} else if A[i][j] < 0 {edges = append(edges, []int{j + 1, i + 1})weights[j][i] = -b[i] / A[i][j]}}}// 添加超级源点for i := 1; i <= n; i++ {edges = append(edges, []int{0, i})weights[0][i-1] = 0.0}// 调用 BellmanFord 算法result, ok := BellmanFord(n, edges, weights)if !ok {fmt.Println("无解")} else {fmt.Println("解:", result)}
}
说明
- 矩阵和向量:假设输入矩阵 A A A 和向量 b b b 已给出。
- 边和权重:根据 A A A 和 b b b 构建图的边和权重。
- 超级源点:引入超级源点,并从该源点到每个节点添加一条权重为 0 的边。
- Bellman-Ford 算法:实现 Bellman-Ford 算法求解最短路径,并检查负权环。
- 整数解检查:确保所有最短路径值为整数。
请注意,这只是一个示例实现,可能需要根据具体情况进行调整。特别是,对于包含浮点数除法的情况,可能需要额外的处理来确保数值稳定性和准确性。





讯飞星火:
解决差分约束系统 A x ≤ b Ax \leq b Ax≤b 的问题,其中变量 x i x_i xi 中某个给定的子集是整数,可以使用线性规划或整数规划的方法。这里我们使用 Go 语言实现一个简单的分支定界法(Branch and Bound)来解决这个问题。
首先,我们需要定义数据结构来表示差分约束系统,然后实现分支定界算法。
package mainimport ("fmt""math"
)// Constraint represents a single constraint in the form of Ax <= b
type Constraint struct {A []float64B float64
}// Node represents a node in the branch and bound tree
type Node struct {level intbound float64solution []float64
}// SolveDifferenceConstraints solves the difference constraint system using branch and bound
func SolveDifferenceConstraints(constraints []Constraint, integerVars []int) ([]float64, bool) {n := len(constraints[0].A) // Number of variablesroot := &Node{level: 0,bound: math.Inf(1), // Positive infinitysolution: make([]float64, n),}var bestSolution []float64bestBound := math.Inf(1)queue := []*Node{root}for len(queue) > 0 {node := queue[0]queue = queue[1:]if node.level == n {if node.bound < bestBound {bestBound = node.boundbestSolution = make([]float64, n)copy(bestSolution, node.solution)}continue}if node.bound >= bestBound {continue}isInteger := falsefor _, i := range integerVars {if i == node.level {isInteger = truebreak}}if isInteger {// Integer variable caseleftChild := &Node{level: node.level + 1,bound: math.Inf(1),solution: make([]float64, n),}copy(leftChild.solution, node.solution)leftChild.solution[node.level] = math.Floor(node.solution[node.level])rightChild := &Node{level: node.level + 1,bound: math.Inf(1),solution: make([]float64, n),}copy(rightChild.solution, node.solution)rightChild.solution[node.level] = math.Ceil(node.solution[node.level])queue = append(queue, leftChild, rightChild)} else {// Continuous variable casechild := &Node{level: node.level + 1,bound: math.Inf(1),solution: make([]float64, n),}copy(child.solution, node.solution)queue = append(queue, child)}}return bestSolution, bestBound != math.Inf(1)
}func main() {constraints := []Constraint{{A: []float64{1, -1}, B: 2},{A: []float64{-1, 1}, B: 0},}integerVars := []int{0} // x0 is an integer variablesolution, found := SolveDifferenceConstraints(constraints, integerVars)if found {fmt.Println("Solution found:", solution)} else {fmt.Println("No solution exists")}
}
解释:
- 数据结构:
Constraint用于表示单个差分约束,Node用于表示分支定界树中的节点。 - SolveDifferenceConstraints:这是主函数,它实现了分支定界算法来解决差分约束系统。对于每个节点,如果当前变量是整数变量,则创建两个子节点分别代表向下取整和向上取整的情况;否则,创建一个子节点继续搜索。
- main:示例代码展示了如何使用
SolveDifferenceConstraints函数来解决一个具体的差分约束系统。
这个实现是一个基本的框架,可以根据具体需求进行优化和扩展。
360智脑:
解决带有整数变量的差分约束系统 ( Ax \leq b ) 可以通过混合整数线性规划 (MILP, Mixed Integer Linear Programming) 来实现。MILP 是一种优化问题,其中一些变量被限制为整数。
算法步骤
-
定义问题:
- 设 ( A ) 是一个 ( m \times n ) 的矩阵。
- ( x ) 是一个 ( n )-维向量,其中某些元素必须是整数。
- ( b ) 是一个 ( m )-维向量,其元素为实数。
-
使用MILP求解器:
- 选择一个MILP求解器,如GLPK、CPLEX、Gurobi等。
- 将问题转换为标准形式并调用求解器。
Go语言实现
下面是一个使用 golang.org/x/sync/errgroup 和 github.com/optimization-tools/go-mip 库的示例代码。假设你已经安装了这些库。
package mainimport ("fmt""github.com/optimization-tools/go-mip"
)func solveMILP(A [][]float64, b []float64, integerIndices []int) (*mip.Model, error) {// 创建一个新的MIP模型model := mip.NewModel()// 添加变量n := len(A[0])vars := make([]*mip.Var, n)for i := 0; i < n; i++ {if contains(integerIndices, i) {// 整数变量vars[i] = model.AddVar(0, mip.Infinity, 0, mip.Int)} else {// 连续变量vars[i] = model.AddVar(0, mip.Infinity, 0, mip.Continuous)}}// 添加约束m := len(A)for i := 0; i < m; i++ {expr := mip.NewLinExpr()for j := 0; j < n; j++ {expr.AddTerm(A[i][j], vars[j])}model.AddConstr(expr, mip.LE, b[i])}// 设置目标函数(这里假设没有目标函数,只是求解可行性问题)model.SetObjective(mip.NewLinExpr(), mip.Minimize)// 求解err := model.Optimize()if err != nil {return nil, err}return model, nil
}func contains(slice []int, val int) bool {for _, item := range slice {if item == val {return true}}return false
}func main() {// 示例数据A := [][]float64{{1, -1, 0},{0, 1, -1},{1, 0, -1},}b := []float64{1, 2, 3}integerIndices := []int{0, 2} // 假设第0和第2个变量是整数model, err := solveMILP(A, b, integerIndices)if err != nil {fmt.Println("Error solving MILP:", err)return}// 输出结果fmt.Println("Solution:")for i, var_ := range model.Vars() {fmt.Printf("x[%d] = %f\n", i, var_.X())}
}
解释
- 创建MIP模型:使用
mip.NewModel()创建一个新的MIP模型。 - 添加变量:根据
integerIndices判断哪些变量是整数,哪些是连续变量,并使用model.AddVar添加变量。 - 添加约束:遍历矩阵
A和向量b,将每个约束添加到模型中。 - 设置目标函数:这里假设没有目标函数,只是求解可行性问题。
- 求解:调用
model.Optimize()求解模型。 - 输出结果:打印出每个变量的解。
注意事项
- 需要安装
github.com/optimization-tools/go-mip库,可以使用以下命令安装:go get github.com/optimization-tools/go-mip - 如果需要更复杂的优化问题,可以调整目标函数和约束条件。
这个示例展示了如何使用Go语言和MILP求解器来解决带有整数变量的差分约束系统。希望对你有帮助!
智谱清言:
差分约束系统是一类特殊的不等式系统,它可以通过图论中的最短路径问题来解决。对于给定的差分约束系统 A x ≤ b Ax \leq b Ax≤b,其中 A A A 是一个系数矩阵, x x x 是变量向量, b b b 是实数向量,并且 x x x 中的某个子集必须是整数,我们可以通过以下步骤来求解:
构建图模型:将每个变量 x i x_i xi 视为一个节点。对于每个不等式 a i j x j − x i ≤ b i a_{ij}x_j - x_i \leq b_i aijxj−xi≤bi,从节点 j j j 到节点 i i i 建立一条边,权重为 b i − a i j b_i - a_{ij} bi−aij。如果 a i j a_{ij} aij 是负数,则从 i i i 到 j j j 建立边,权重为 − b i − a i j -b_i - a_{ij} −bi−aij。
添加虚拟源点:添加一个虚拟源点,从该源点向所有其他节点建立边,权重为 0。
求解最短路径:使用单源最短路径算法(如贝尔曼-福特算法)来求解从虚拟源点出发到所有其他点的最短路径。
整数约束处理:如果 x i x_i xi 必须是整数,那么在图中对应节点的最短路径值需要向下取整(或者向上取整,取决于约束条件)。
负权重循环检测:如果在求解最短路径的过程中发现了负权重循环,那么差分约束系统无解。
下面是用 Go 语言实现的一个简化版本,只考虑整数约束,并使用贝尔曼-福特算法:
package main
import (
“fmt”
“math”
)
// Edge represents an edge in the graph
type Edge struct {
from int
to int
weight int
}
// BellmanFord solves the single source shortest path problem
func BellmanFord(edges []Edge, numVertices int, source int) ([]int, bool) {
dist := make([]int, numVertices)
for i := range dist {
dist[i] = math.MaxInt64
}
dist[source] = 0
for i := 0; i < numVertices-1; i++ {
for _, edge := range edges {
if dist[edge.from] != math.MaxInt64 && dist[edge.from]+edge.weight < dist[edge.to] {
dist[edge.to] = dist[edge.from] + edge.weight
}
}
}
// Check for negative-weight cycles
for _, edge := range edges {
if dist[edge.from] != math.MaxInt64 && dist[edge.from]+edge.weight < dist[edge.to] {
return nil, false // Negative cycle detected
}
}
return dist, true
}
func main() {
// Example usage
// A = [[-1, 1], [1, 0], [0, -1]]
// b = [0, 3, 2]
// x1, x2 are variables
// x1 - x2 <= 0
// x1 + x2 <= 3
// -x2 <= 2
edges := []Edge{
{0, 1, 0}, // x1 - x2 <= 0 => x2 - x1 <= 0
{1, 0, 3}, // x1 + x2 <= 3 => -x1 - x2 <= -3
{2, 1, 2}, // -x2 <= 2 => x2 <= 2
}
numVariables := 3
source := 3 // Virtual source node
dist, noNegativeCycle := BellmanFord(edges, numVariables+1, source)
if !noNegativeCycle {
fmt.Println(“The system has no solution due to a negative-weight cycle.”)
return
}
// Apply integer constraints
for i := 0; i < numVariables; i++ {
dist[i] = int(math.Floor(float64(dist[i]))) // Assuming down constraint
}
fmt.Println(“The solution is:”, dist[:numVariables])
}
在这个例子中,我们假设了 numVariables 是变量数量,并且 source 是虚拟源点的索引。dist 数组存储了从虚拟源点到每个节点的最短路径长度。注意,这个代码示例没有实现整数约束的优化处理,只是简单地使用了向下取整。在实际问题中,可能需要更复杂的处理来满足整数约束。
天工:
-
算法原理
- 差分约束系统可以转化为图论中的单源最短路径问题。对于每个约束条件(x_j - x_i\leqslant b_k),可以构建一条从节点(i)到节点(j)的有向边,边的权值为(b_k)。
- 如果要求变量(x_i)中的某个给定子集是整数,可以在求最短路径的算法中进行特殊处理。这里我们可以使用Bellman - Ford算法,它可以处理负权边并且能检测负权环。
-
Go语言实现示例
package mainimport ("fmt""math" )// BellmanFord算法解决差分约束系统,部分变量为整数 func BellmanFord(A [][]int, b []float64, integerVars []int) []float64 {n := len(A)dist := make([]float64, n)for i := range dist {dist[i] = math.Inf(1)}dist[0] = 0// 进行n - 1次松弛操作for i := 0; i < n - 1; i++ {for j := 0; j < len(A); j++ {for k := 0; k < len(A[j]); k++ {if dist[A[j][k]] > dist[j]+b[j] {dist[A[j][k]] = dist[j] + b[j]}}}}// 检查负权环for j := 0; j < len(A); j++ {for k := 0; k < len(A[j]); k++ {if dist[A[j][k]] > dist[j]+b[j] {fmt.Println("存在负权环,无解")return nil}}}// 处理整数变量for _, varIndex := range integerVars {dist[varIndex] = math.Floor(dist[varIndex])}return dist }你可以使用以下方式调用这个函数:
func main() {// 这里只是一个简单示例,实际使用时根据具体的A和b来定义A := [][]int{{1}, {0}}b := []float64{5, -3}integerVars := []int{0}result := BellmanFord(A, b, integerVars)if result!= nil {fmt.Println(result)} }在这个代码中,
BellmanFord函数首先初始化距离数组dist,然后进行(n - 1)次松弛操作来更新最短路径距离。接着检查是否存在负权环,如果存在则输出无解。最后,如果有指定的整数变量,将其距离值向下取整。
chatgpt:
差分约束系统可以使用 Bellman-Ford 算法来求解,特别是在处理有负权边的情况下。为了处理整数变量,我们可以引入整数线性规划 (ILP) 的技术。这里提供一个基本的框架来解决差分约束系统 ( Ax \leq b ) 的问题,同时处理整数约束。我们将使用 Go 语言进行实现。
首先,我们需要解释一下算法的关键步骤:
- 表述约束:将约束表示为图中的边,其中每个边具有权重。
- 使用 Bellman-Ford 算法:寻找最短路径并检测负环。
- 处理整数变量:如果有变量是整数的,可以使用分支限界法或其他整数优化技术。
以下是使用 Go 语言实现的一个简单示例代码,处理差分约束系统 ( Ax \leq b )。
package mainimport ("fmt""math"
)// Edge represents a directed edge in the graph with a weight.
type Edge struct {from, to, weight int
}// BellmanFord function to find shortest path in a graph with possible negative weights
func BellmanFord(edges []Edge, vertexCount, source int) ([]float64, error) {distances := make([]float64, vertexCount)for i := range distances {distances[i] = math.MaxFloat64 // Initialize distances to infinity}distances[source] = 0 // Distance to source is 0// Relax edges repeatedlyfor i := 0; i < vertexCount-1; i++ {for _, edge := range edges {if distances[edge.from] != math.MaxFloat64 && distances[edge.from]+float64(edge.weight) < distances[edge.to] {distances[edge.to] = distances[edge.from] + float64(edge.weight)}}}// Check for negative-weight cyclesfor _, edge := range edges {if distances[edge.from] != math.MaxFloat64 && distances[edge.from]+float64(edge.weight) < distances[edge.to] {return nil, fmt.Errorf("negative weight cycle detected")}}return distances, nil
}// SolveDiffConstraintSystem solves Ax ≤ b using Bellman-Ford
func SolveDiffConstraintSystem(A [][]int, b []int) ([]int, error) {vertexCount := len(A)var edges []Edge// Create edges based on the constraintsfor i := 0; i < vertexCount; i++ {for j := 0; j < vertexCount; j++ {if A[i][j] != 0 {edges = append(edges, Edge{from: i, to: j, weight: -A[i][j]})}}}// Add edges for the inequalities b[i]for i := 0; i < vertexCount; i++ {edges = append(edges, Edge{from: i, to: vertexCount - 1, weight: b[i]})}distances, err := BellmanFord(edges, vertexCount+1, vertexCount-1)if err != nil {return nil, err}// The resulting distances can be adjusted for the integer constraintsreturn distances[:vertexCount], nil // Return the result excluding the last vertex
}func main() {A := [][]int{{0, 1, 1}, // x_1 - x_0 <= 1{-1, 0, 2}, // x_2 - x_1 <= 2{3, -1, 0}, // x_0 - x_2 <= 3}b := []int{1, 2, 3}result, err := SolveDiffConstraintSystem(A, b)if err != nil {fmt.Println("Error:", err)return}fmt.Println("Result:", result)
}
代码解释:
- Edge 结构体:用于表示图的边。
- BellmanFord:实现了 Bellman-Ford 算法来寻找最短路径,处理可能的负权重边。
- SolveDiffConstraintSystem:构建图并调用 Bellman-Ford 算法来解决差分约束问题。
- main 函数:定义了约束矩阵 ( A ) 和向量 ( b ),并调用求解函数。
注意事项:
- 该代码未处理整数约束,需要根据实际情况进一步实现。
- 这个实现仅是一个基础示例,对于大型或复杂的差分约束系统,可能需要使用更专业的 ILP 库(例如 Gurobi 或其他库)。
kimi:
解决 (Ax \leq b) 的差分约束系统,其中 (b) 的所有元素为实数,而变量 (x_i) 中某个给定的子集是整数,可以通过多种算法实现。这里,我将介绍一种基于线性规划(Linear Programming, LP)的方法,特别是使用分支定界(Branch and Bound)算法来处理整数变量的情况。这种方法适用于解决混合整数线性规划(Mixed-Integer Linear Programming, MILP)问题。
算法概述
-
线性规划松弛:首先,忽略整数约束,将问题视为一个线性规划问题来解决。这可以通过使用单纯形法(Simplex Method)或其他LP求解器来完成。
-
分支:如果线性规划的解包含非整数变量,选择一个非整数变量进行分支。通常选择分数部分最大的变量。
-
定界:对于选定的非整数变量,创建两个子问题:一个子问题中该变量被固定为小于或等于其整数部分,另一个子问题中该变量被固定为大于或等于其下一个整数。这称为分支。
-
求解子问题:对每个子问题重复步骤1和2,直到所有变量都是整数或子问题无解。
-
剪枝:如果某个子问题的解不满足原始约束或目标函数值超过已知的最佳解,则可以剪枝,即不再进一步探索该子问题。
-
最优解:当所有变量都是整数时,如果满足所有约束,则该解是最优解。
Go语言实现
Go语言本身没有内置的线性规划求解器,但可以使用第三方库,如gonum中的mat包来构建和解决LP问题。对于MILP,你可能需要使用外部求解器,如CPLEX、Gurobi或COIN-OR等,并通过Go语言调用它们。
以下是一个简化的Go语言代码框架,展示如何设置问题并调用外部求解器(假设使用CPLEX):
package mainimport ("fmt""gonum.org/v1/gonum/mat"
)func main() {// 定义矩阵A和向量bA := mat.NewDense(3, 3, []float64{1, 1, 1, 1, 2, 1, 1, 1, 3})b := []float64{10, 20, 30}// 定义变量的界限varLB := []float64{0, 0, 0} // 下界varUB := []float64{100, 100, 100} // 上界// 调用外部求解器(这里只是示例,实际需要调用CPLEX等)solveLP(A, b, varLB, varUB)// 检查是否有非整数解,并进行分支定界checkForIntegerSolution()
}func solveLP(A *mat.Dense, b, varLB, varUB []float64) {// 这里应该是调用LP求解器的代码// 例如,使用CPLEX的Go接口fmt.Println("Solving LP...")
}func checkForIntegerSolution() {// 检查解是否为整数,如果不是,则进行分支fmt.Println("Checking for integer solution...")
}
请注意,这只是一个框架,实际实现需要根据你选择的求解器进行调整。对于MILP问题,你可能需要使用专门的MILP求解器,并在Go中通过接口调用它们。这可能涉及到更复杂的设置,包括设置变量类型(连续或整数)和处理求解器的输出。
混元:
要解决一个包含整数变量的差分约束系统 (Ax \leq b),我们可以使用图论中的最短路径算法。具体来说,我们可以将每个不等式 (a_{ij}x_j \leq a_{ii}x_i + b_{ij}) 转换为一个有向边 ((j, i)) 的权重为 (b_{ij} / a_{ij})。然后,我们可以使用Bellman-Ford算法或Dijkstra算法(如果图中没有负权重边)来找到从源点到所有其他点的最短路径。
以下是用Go语言实现的解决方案:
package mainimport ("fmt""math"
)type Edge struct {to intweight float64
}func BellmanFord(edges [][]Edge, source int, n int) ([]float64, bool) {dist := make([]float64, n)for i := range dist {dist[i] = math.Inf(1)}dist[source] = 0for i := 0; i < n-1; i++ {for u := 0; u < n; u++ {for _, edge := range edges[u] {v := edge.toif dist[u]+edge.weight < dist[v] {dist[v] = dist[u] + edge.weight}}}}// Check for negative-weight cyclesfor u := 0; u < n; u++ {for _, edge := range edges[u] {v := edge.toif dist[u]+edge.weight < dist[v] {return nil, false // Negative cycle detected}}}return dist, true
}func solveDifferentialConstraints(A [][]float64, b []float64, integerIndices []int) ([]float64, bool) {n := len(b)edges := make([][]Edge, n)for i := 0; i < n; i++ {for j := 0; j < n; j++ {if A[i][j] != 0 {weight := b[i] / A[i][j]edges[j] = append(edges[j], Edge{to: i, weight: weight})}}}// Add a source node connected to all integer variables with weight 0source := nedges = append(edges, make([]Edge, n))for _, idx := range integerIndices {edges[source] = append(edges[source], Edge{to: idx, weight: 0})}dist, ok := BellmanFord(edges, source, n+1)if !ok {return nil, false // Negative cycle detected}result := make([]float64, n)for i := 0; i < n; i++ {result[i] = dist[i]}return result, true
}func main() {A := [][]float64{{0, 1, 0},{-1, 0, 1},{0, -1, 0},}b := []float64{3, 3, 0}integerIndices := []int{0}result, ok := solveDifferentialConstraints(A, b, integerIndices)if ok {fmt.Println("Solution:", result)} else {fmt.Println("No solution exists")}
}
解释
-
数据结构:
Edge结构体表示图中的边,包含目标节点to和权重weight。edges是一个二维切片,表示图的邻接表。
-
Bellman-Ford算法:
- 初始化距离数组
dist,将源点的距离设为0,其他点的距离设为无穷大。 - 进行
n-1次松弛操作,尝试更新每条边的目标节点的距离。 - 检查是否存在负权重环,如果存在则返回
false。
- 初始化距离数组
-
差分约束系统转换:
- 将每个不等式 (a_{ij}x_j \leq a_{ii}x_i + b_{ij}) 转换为边 ((j, i)) 的权重为 (b_{ij} / a_{ij})。
- 添加一个源节点,连接到所有整数变量,权重为0。
-
主函数:
- 定义矩阵
A和向量b,以及整数变量的索引。 - 调用
solveDifferentialConstraints函数求解差分约束系统,并输出结果。
- 定义矩阵
这个算法可以处理包含整数变量的差分约束系统,并且能够检测负权重环的情况。
相关文章:

文心一言 VS 讯飞星火 VS chatgpt (380)-- 算法导论24.4 12题
十二、给出一个有效算法来解决 A x ⩽ b Ax⩽b Ax⩽b 的差分约束系统,这里 b b b 的所有元素为实数,而变量 x i x_i xi 中某个给定的子集是整数。如果要写代码,请用go语言。 文心一言: 差分约束系统问题通常用于解决带有约…...
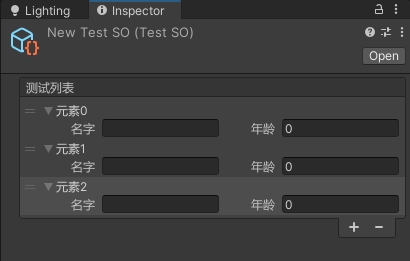
Unity自定义数组在Inspector窗口的显示方式
了解 单行高度:EditorGUIUtility.singleLineHeight获取 PropertyField 控件所需的高度:EditorGUI.GetPropertyHeight属性是否在Inspector窗口展开:SerializedProperty.isExpanded可重新排序列表类:ReorderableList绘制纯色矩形:EditorGUI.Dr…...
--SPCL论文阅读笔记(2024-10-29))
ERC论文阅读(03)--SPCL论文阅读笔记(2024-10-29)
SPCL论文阅读笔记 论文中心思想 这篇论文是研究ERC任务的论文,作者提出了监督原型对比学习的方法用于ERC任务。 论文 EMNLP2022 paper “Supervised Prototypical Contrastive Learning for Emotion Recognition in Conversation” 现存问题 现存的使用监督对…...

Straightforward Layer-wise Pruning for More Efficient Visual Adaptation
对于模型中冗余的参数,一个常见的方法是通过结构化剪枝方法减少参数容量。例如,基于幅度值和基于梯度的剪枝方法。尽管这些方法在传统训练上通用性,本文关注的PETL迁移有两个不可避免的问题: 显著增加了模型存储负担。由于不同的…...

喜讯 | 创邻科技杭州电子科技大学联合实验室揭牌成立!
近日,杭州电子科技大学图书情报专业硕士行业导师聘任仪式暨杭电-创邻图技术与数字化联合实验室(图书档案文物数字云联合研发中心)揭牌仪式在杭州电子科技大学隆重举行。杭州电子科技大学原副校长吕金海、研究生院副院长潘建江,科研…...

海外媒体发稿:如何打造媒体发稿策略
新闻媒体的发稿推广策略对于提升品牌知名度、吸引流量以及增加收入非常重要。本文将介绍一套在21天内打造爆款新闻媒体发稿推广策略的方法。 第一天至第七天:明确目标和定位 在这个阶段,你需要明确你的目标和定位,以便为你的新闻媒体建立一个…...

PyTorch模型保存与加载
1.保存与加载的概念(序列化与反序列化) 模型训练完毕之后,肯定想要把它保存下来,供以后使用,不需要再次去训练。 那么在pytorch中如何把训练好的模型,保存,保存之后又如何加载呢? 这就用需要序列化与反序列化,序列化与反序列化的概念如下图所示: 因为在内…...
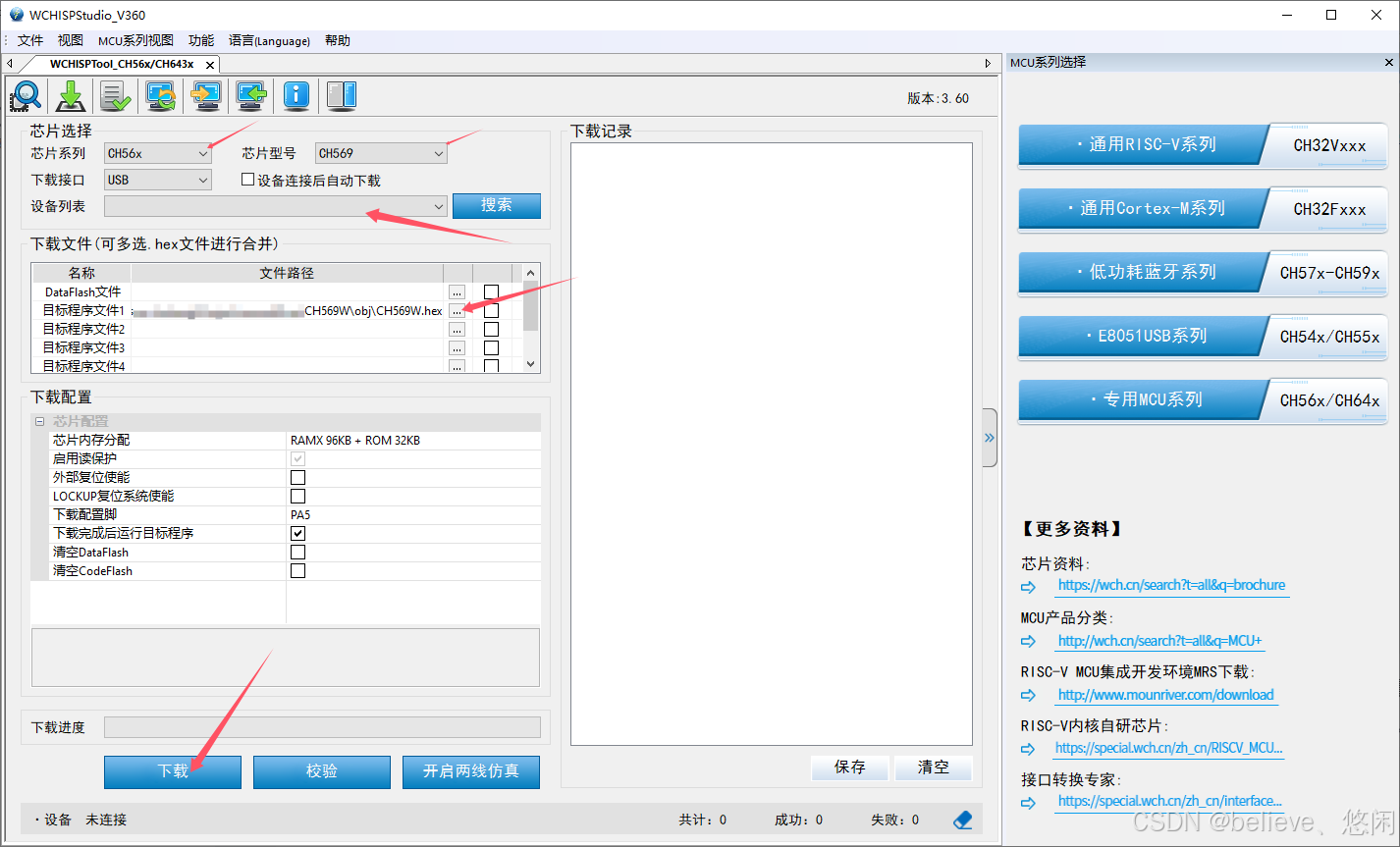
CH569开发前的测试
为了玩转准备Ch569的开发工作 ,准备了如下硬件和软件: 硬件 1.官方的 Ch569 开发板,官方买到的是两块插接在一起的;除了HSPI接口那里的电阻,这两块可以说是一样的。也意味着两块板子的开发也需要烧录两次;…...
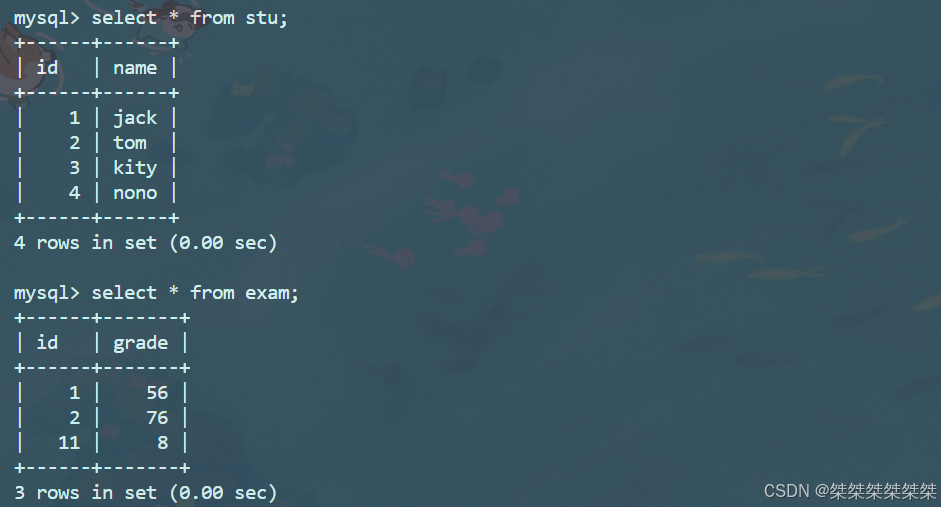
MySQL中表的外连接和内连接
内连接和外连接 表的连接分为内连接和外连接,内连接就是将需要连接的表形成笛卡尔积筛选;外连接分为左外连接和右外连接,左外连接为左侧的表需要完全显示,右外连接为右侧的表现需要完全显示。 文章目录 内连接和外连接内连接外…...

Ubuntu 上安装 Redmine 5.1 指南
文章目录 官网安装文档:命令步骤相关介绍GemRubyRailsBundler 安装 Redmine更新系统包列表和软件包:安装必要的依赖:安装 Ruby:安装 bundler下载 Redmine 源代码:安装 MySQL配置 Redmine 的数据库配置文件:…...
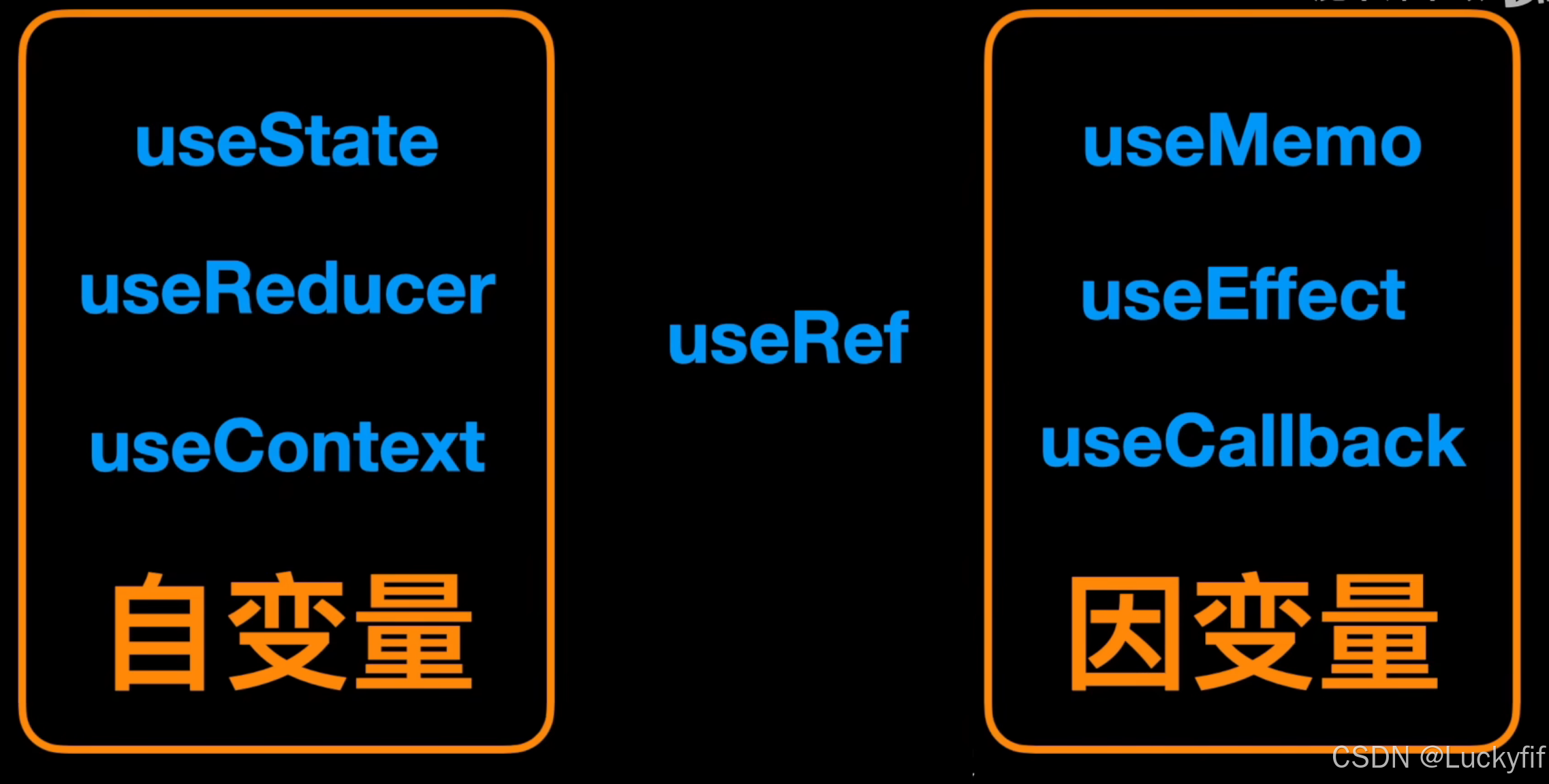
从变量的角度理解 Hooks , 变得更简单了
从变量角度理解Hooks 在React的世界里,Hooks的引入为函数式组件带来了前所未有的灵活性和能力。它们让我们得以完全摆脱class式的写法,在函数式组件中完成生命周期管理、状态管理、逻辑复用等几乎全部组件开发工作。这次,我们就从变量的角度…...
LabVIEW Modbus通讯稳定性提升
在LabVIEW开发Modbus通讯程序时,通讯不稳定是一个常见问题,可能导致数据丢失、延迟或错误。为了确保通讯的可靠性,可以从多个角度进行优化,以下是一些有效的解决方案,结合实际案例进行分析。 1. 优化通讯参数设置 通讯…...
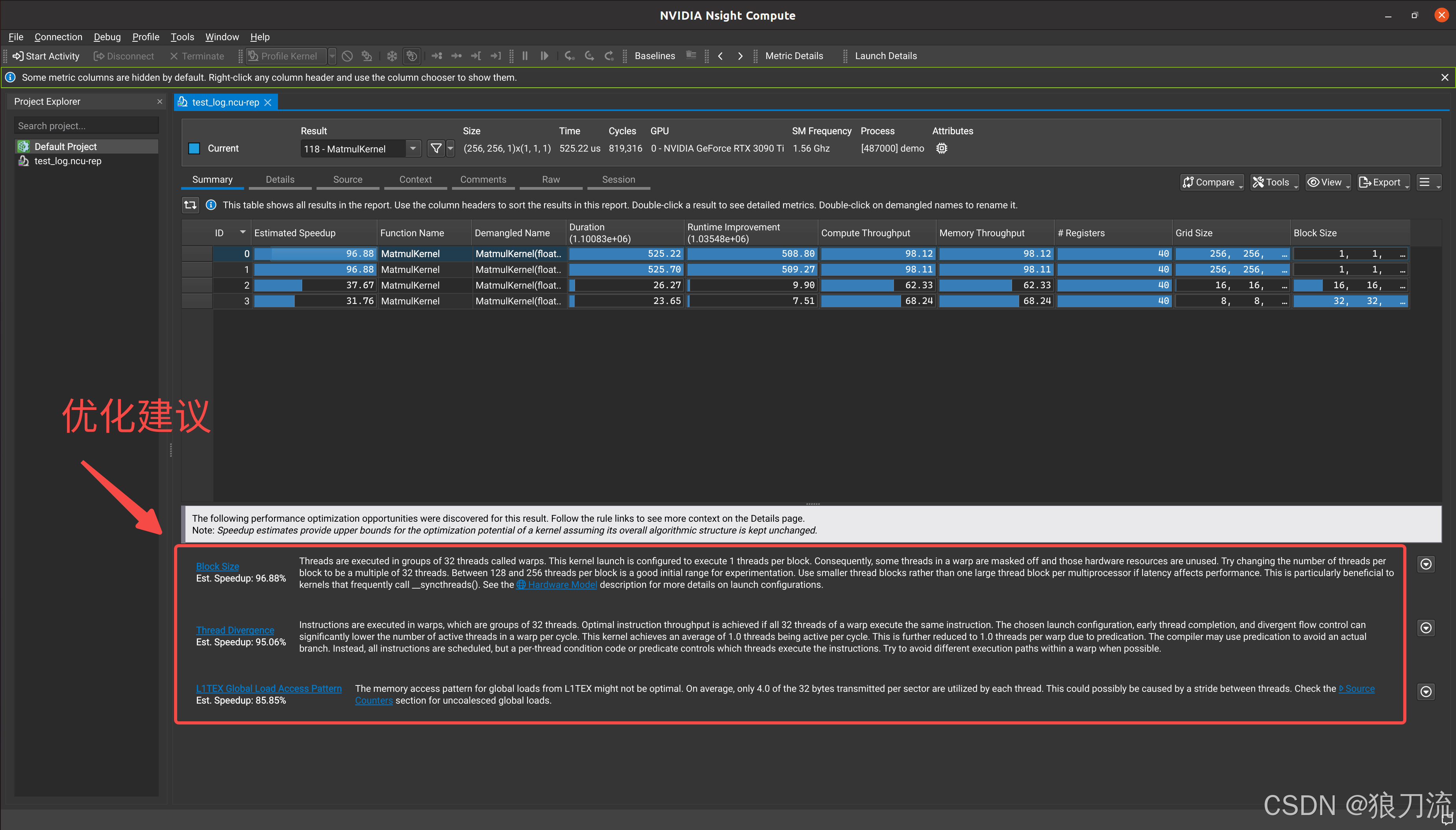
(8) cuda分析工具
文章目录 Nvidia GPU性能分析工具Nsight SystemNvidia GPU性能分析工具Nsight System Nvidia GPU性能分析工具Nsight System NVIDIA Nsight Systems是一个系统级的性能分析工具,用于分析和优化整个CUDA应用程序或系统的性能。它可以提供对应用程序整体性能的全面见…...

C语言 | Leetcode C语言题解之第517题超级洗衣机
题目: 题解: int findMinMoves(int* machines, int machinesSize){int sum0;for(int i0;i<machinesSize;i){summachines[i];}if(sum%machinesSize!0){return -1;}int psum/machinesSize;int ans0;int cur0;for(int i0;i<machinesSize;i){cur(mac…...

Java多线程编程基础
目录 编写第一个多线程程序 1. 方式一 : 继承Thread类, 重写run方法 2. 方式二: 实现Runnable接口, 重写run方法 3. 方式三: 使用Lambda表达式 [匿名内部类] [Lambda表达式] 在上个文章中, 我们了解了进程和线程的相关概念. 那么, 在Java中, 我们如何进行多线程编程呢? …...

刷代随有感(134):单调栈——下一个更大元素I(难点涉及哈希表与单调栈的结合)
单调栈处理的是下标! 题干: 代码: class Solution { public:vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) {stack<int>ddst;unordered_map<int,int>umap;vector<int…...
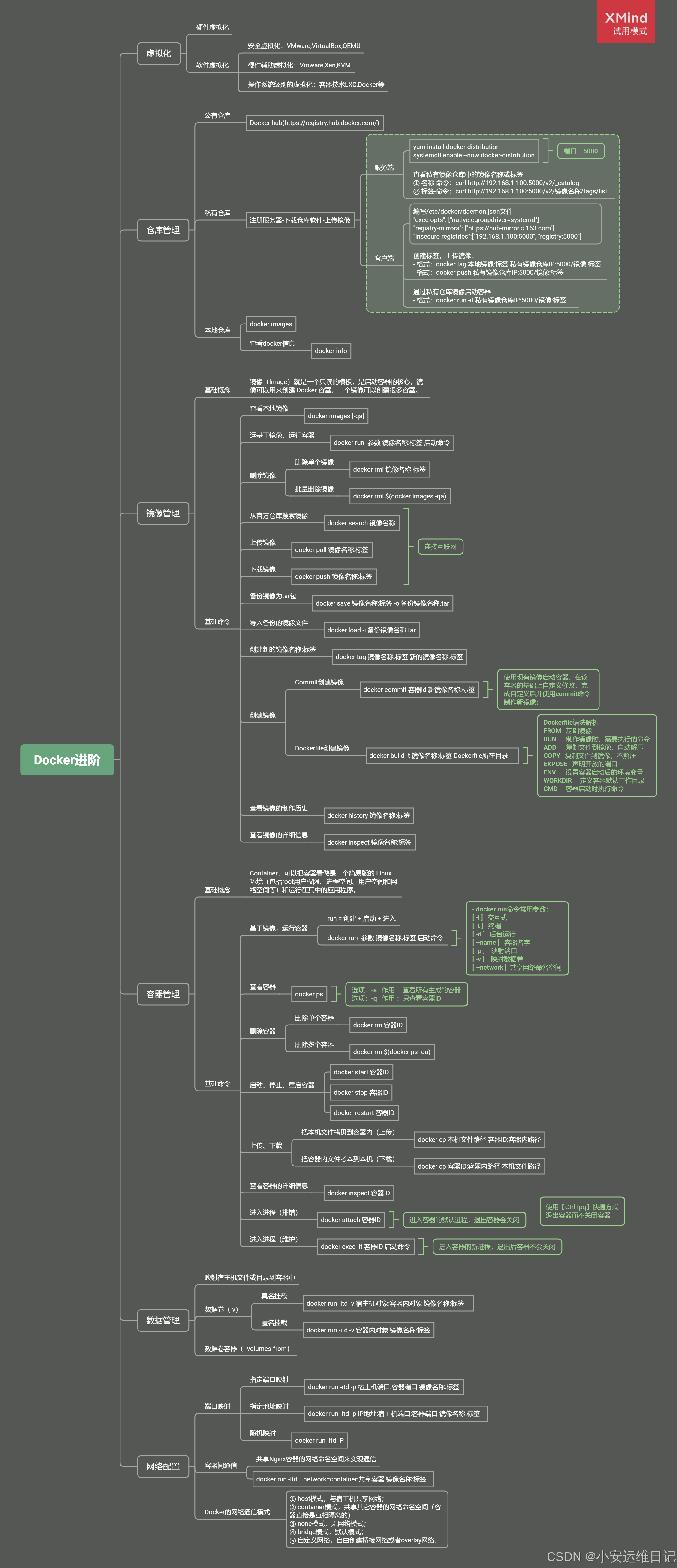
Linux云计算 |【第五阶段】CLOUD-DAY5
主要内容: 容器的镜像编排,commit简单镜像创建,Dockerfile制作服务镜像(语法、创建镜像)、创建复杂镜像(Docker微服务架构、示例:NGINXPHP)、私有仓库 一、简单镜像创建 1、自定义…...

被上传文件于后端的命名策略
上一篇博客我们了解了前端上传的文件资源应该存放在后端项目中的什么位置,那么随之而来的另一个问题——我们应该如何为上传的文件命名呢?往往直接采用原文件名并不稳妥,会导致命名冲突、文件冲突、数据库管理冲突等多种问题,下面…...

哈希表 算法专题
哈希表简介 是什么 存储数据的容器有啥用? "快速"查找某个元素什么时候用哈希表 频繁地查找某个数(有序用二分)怎么用哈希表 容器用数组模拟 字符串中的字符 范围比较小的数 一. 两数之和 两数之和 class Solution {public int[] twoSum(int[] nums, int targe…...

unity3d————[HideInInspector]
在Unity3D中,[HideInInspector]是一个属性修饰符,它的主要作用是在Unity的Inspector窗口中隐藏变量或属性。以下是关于[HideInInspector]的详细解释和作用: 作用 隐藏变量或属性:当你在脚本中使用[HideInInspector]修饰符时&…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...
